1.5: Isometrías, movimientos y líneas

Última actualización
Guardar como PDF

Page ID: 114771

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, definimos líneas en un espacio métrico. Una vez hecha la oración “Podemos trazar una línea única que pasa por dos puntos dados.” se vuelve rigurosa; ver (ii) en la Sección 1.1.

Recordemos que un mapa$f: \mathcal{X} \to \mathcal{Y}$ es una biyección, si da un emparejamiento exacto de los elementos de dos conjuntos. Equivalentemente,$f: \mathcal{X} \to \mathcal{Y}$ es una biyección, si tiene una inversa; es decir, un mapa$g: \mathcal{Y} \to \mathcal{X}$ tal que$g(f(A)) = A$ para cualquiera$A \in \mathcal{X}$ y$f(g(B)) = B$ para cualquiera$B \in \mathcal{Y}$.

Dejar$\mathcal{X}$ y$\mathcal{Y}$ ser dos espacios métricos y$d_{\mathcal{X}}$,$d_{\mathcal{Y}}$ ser sus métricas. Un mapa

\[f: \mathcal{X} \to \mathcal{Y}\]

se llama preservación de distancia si

\[d_{\mathcal{Y}} (f(A), f(B)) = d_{\mathcal{X}} (A, B)\]

para cualquier$A, B \in \mathcal{X}$.

Definición

Un mapa biyective que preserva la distancia se llama isometría.
Dos espacios métricos se denominan isométricos si existe una isometría de uno a otro.
La isometría de un espacio métrico a sí mismo también se llama movimiento del espacio.

Ejercicio$\PageIndex{1}$

Mostrar que cualquier mapa de preservación de distancia es inyectivo; es decir, si$f: \mathcal{X} \to \mathcal{Y}$ es un mapa que preserva la distancia, entonces$f(A) \ne f(B)$ para cualquier par de puntos distintos$A, B \in \mathcal{X}$.

Pista

Si$A \ne B$, entonces$d_{\mathcal{X} (A, B) > 0$. Dado que$f$ es la preservación de la distancia,

$d_{\mathcal{Y}} (f(A), f(B)) = d_{\mathcal{X}} (A, B)$.

Por lo tanto,$d_{\mathcal{Y}} (f(A), f(B)) > 0$; de ahí$f(A) \ne f(B)$.

Ejercicio$\PageIndex{2}$

Demuestre que si$f: \mathbb{R} \to \mathbb{R}$ es un movimiento de la línea real, entonces ya sea

(a)$f(x) = f(0) + x$ para cualquiera$x \in \mathbb{R}$, o

(b)$f(x) = f(0) - x$ para cualquier$x \in \mathbb{R}$.

Pista

Establecer$f(0) = a$ y$f(1) = b$. Tenga en cuenta que$b = a + 1$ o$a - 1$. Por otra parte,$f(x) = a \pm x$ y a la vez,$f(x) = b \pm (x - 1)$ para cualquier$x$.

Si$b = a + 1$, se deduce que$f(x) = a + x$ para alguna$x$.
De la misma manera, si$b = a - 1$, se deduce que$f(x) = a - x$ para cualquiera$x$.

Ejercicio$\PageIndex{3}$

Demostrar que$(\mathbb{R}^2, d_1)$ es isométrico a$(\mathbb{R}^2, d_{\infty})$.

Pista: Mostrar que el mapa$(x, y) \mapsto (x + y, x - y)$ es una isometría$(\mathbb{R}^2, d_1) \to (\mathbb{R}^2, d_{\infty})$. Es decir, es necesario verificar si este mapa es biyective y preserva la distancia.

Ejercicio Avanzado$\PageIndex{4}$

Describir todos los movimientos del avión Manhattan, definidos en la Sección 1.4.

Pista

Primero probar que dos puntos$A = (x_A, y_A)$ y$B = (x_B, y_B)$ en el avión Manhattan tienen un punto medio único si y sólo si$x_A = x_B$ o$y_A = y_B$; comparar con el ejemplo en triángulos congruentes.

Luego use la declaración anterior para probar que cualquier movimiento del avión de Manhattan puede escribirse de una de las siguientes dos maneras:

$(x, y) \mapsto (\pm x + a, \pm y + b)$o$(x, y) \mapsto (\pm y + b, \pm x + a)$,

para algunos números reales fijos$a$ y$b$. (En cada caso tenemos 4 opciones de signos, así que para un par fijo$(a, b)$ tenemos 8 movimientos distintos).

Si$\mathcal{X}$ es un espacio métrico y$\mathcal{Y}$ es un subconjunto de$\mathcal{X}$, entonces se$\mathcal{Y}$ puede obtener una métrica encendida restringiendo la métrica de$\mathcal{X}$. En otras palabras, la distancia entre dos puntos de$\mathcal{Y}$ se define como la distancia entre estos puntos en$\mathcal{X}$. De esta manera, cualquier subconjunto de un espacio métrico también puede considerarse como un espacio métrico.

Definición

Un subconjunto$l$ de espacio métrico se llama línea, si es isométrico a la línea real.

Un triple de puntos que se encuentran en una línea se llama colineal. Tenga en cuenta que si$A$$B$,, y$C$ son colineales,$AC \ge AB$ y$AC \ge BC$, entonces$AC = AB + BC$.

Algunos espacios métricos no tienen líneas, por ejemplo métricas discretas. En la imagen se muestran ejemplos de líneas en el avión de Manhattan$(\mathbb{R}^2, d_1)$.

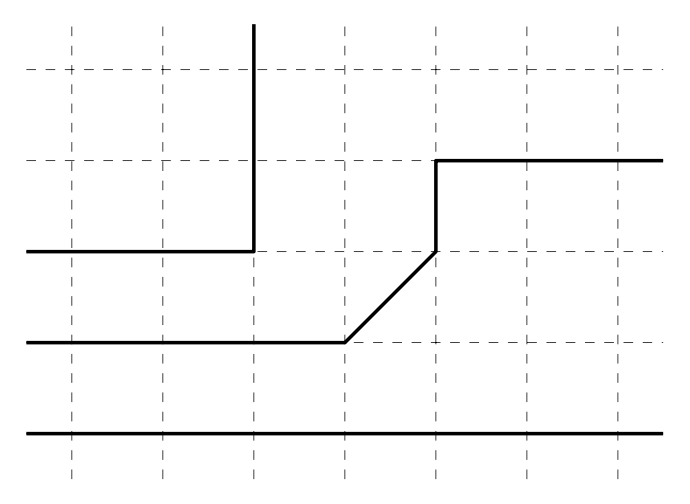
$2021-01-28 12.49.09.png$

Ejercicio$\PageIndex{5}$

Considera la gráfica$y = |x|$ en$\mathbb{R}^2$. ¿En cuál de los siguientes espacios (a)$(\mathbb{R}^2, d_1)$, (b)$(\mathbb{R}^2, d_2)$, (c)$(\mathbb{R}^2, d_{\infty})$ forma una línea? ¿Por qué?

Pista

Asumir tres puntos$A, B$, y se$C$ encuentran en una línea, Tenga en cuenta que en este caso una de las desigualdades triangulares con los puntos$A, B$, y$C$ se convierte en una igualdad.

Establecer$A = (-1, 1)$,$B = (0, 0)$, y$C = (1, 1)$. Demostrar que para$d_1$ y$d_2$ todas las desigualdades triangulares con los puntos$A, B$, y$C$ son estrictas. De ello se deduce que la gráfica no es una línea.

Para$d_{\infty}$ espectáculo que$(x, |x|) \mapsto x$ da la isometría de la gráfica a$\mathbb{R}$. Concluir que la gráfica es una línea en$(\mathbb{R}^2, d_{\infty})$.

Ejercicio$\PageIndex{6}$

Demuestre que cualquier movimiento mapea una línea a una línea.

Pista: Deletrea las definiciones de línea y movimiento.