2.4: Ángulo recto

Última actualización
Guardar como PDF

Page ID: 114578

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Si$\measuredangle AOB = \pi$, decimos que$\angle AOB$ es un ángulo recto. Obsérvese que por la Proposición 2.3.2, si$\angle AOB$ es una recta, entonces también lo es$\angle BOA$.

Nosotros dice que el punto$O$ se encuentra entre los puntos$A$ y$B$, si$O \ne A$,$O \ne B$, y$O \in [AB]$.

Teorema$\PageIndex{1}$

El ángulo$AOB$ es recto si y solo si$O$ se encuentra entre$A$ y$B$.

Prueba

Por la Proposición 2.2.2, podemos suponer que$OA = OB = 1$.

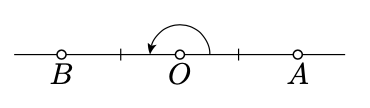
$2021-02-02 10.04.24.png$

“Si” parte. Asumir$O$ mentiras entre$A$ y$B$. Set$\alpha = \measuredangle AOB$.

Aplicando Axioma IIIa, obtenemos una media línea$[OA')$ tal que$\alpha = \measuredangle BOA'$. Por la Proposición 2.2.2, podemos asumir eso$OA' = 1$. Según Axioma IV,

$\triangle AOB \cong \triangle BOA'$.

Supongamos que$f$ denota el movimiento correspondiente del plano; es decir,$f$ es un movimiento tal que$f(A) = B$,$f(O) = O$, y$f(B) = A'$.

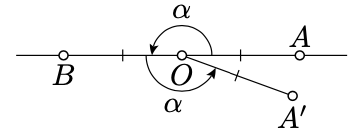
$2021-02-02 10.04.45.png$

Entonces

$O = f(O) \in f(AB) = (A'B)$.

Por lo tanto, ambas líneas$(AB)$ y$(A'B)$ contienen$B$ y$O$. Por Axioma II,$(AB) = (A'B)$.

Por la definición de la línea,$(AB)$ contiene exactamente dos puntos$A$ y$B$ en la distancia 1 de$O$. Desde$OA' = 1$ y$A' \ne B$, lo conseguimos$A = A'$.

Por Axioma IIIb y Proposición 2.3.1, lo conseguimos

\[\begin{array} {rcl} {2 \cdot \alpha} & = & {\measuredangle AOB + \measuredangle BOA' =} \\ {} & = & {\measuredangle AOB + \measuredangle BOA \equiv} \\ {} & equiv & {\measuredangle AOA =} \\ {} & = & {0} \end{array}\]

Por lo tanto, por el Ejercicio 1.8.1,$\alpha$ es 0 o$\pi$.

Ya que$[OA) \ne [OB)$, tenemos eso$\alpha \ne 0$, ver Ejercicio 2.3.1. Por lo tanto,$\alpha = \pi$.

“Sólo si” parte. Supongamos que$\measuredangle AOB = \pi$. Considera la línea$(OA)$ y elige un punto$B'$ sobre$(OA)$ para que$O$ quede entre$A$ y$B'$.

Desde arriba, tenemos eso$\measuredangle AOB' = \pi$. Aplicando Axioma IIIa, lo conseguimos$[OB) = [OB')$. En particular,$O$ se encuentra entre$A$ y$B$.

Un triángulo$ABC$ se llama degenerado si$A, B$, y$C$ se encuentra en una línea. El siguiente corolario es solo una reformulación del Teorema 2.4.1.

Corolario$\PageIndex{1}$

Un triángulo es degenerado si y sólo si uno de sus ángulos es igual$\pi$ o 0. Además, en un triángulo degenerado las medidas del ángulo son 0, 0 y$\pi$.

Ejercicio$\PageIndex{1}$

Mostrar que tres puntos distintos$A, O$, y$B$ se encuentran en una línea si y sólo si

$2 \cdot \measuredangle AOB \equiv 0$.

Pista: Aplicar la Proposición 2.3.1, Teorema 2.4.1 y Ejercicio 1.8.1.

Ejercicio$\PageIndex{2}$

Dejar$A, B$ y$C$ ser tres puntos distintos de$O$. $B, O$Muéstralo y$C$ acuéstate en una línea si y solo si

$2 \cdot \measuredangle AOB \equiv 2 \cdot \measuredangle AOC$.

Pista: Axioma IIIb,$2 \cdot \measuredangle BOC \equiv 2 \cdot \measuredangle AOC - 2 \cdot \measuredangle AOB = 0$. Por el Ejercicio 1.8.1, implica que$\measuredangle BOC$ es 0 o$\pi$. Queda por aplicar Exercsie 2.3.1 y Teorema 2.4.1 respectivamente en estos dos casos.

Ejercicio$\PageIndex{3}$

Demostrar que hay un triángulo no degenerado.

Contestar

Fijar dos puntos$A$ y$B$ proporcionados por Axioma I.

Arreglar un número real$0 < \alpha < \pi$. Por Axioma IIIa hay un punto$C$ tal que$\measuredangle ABC = \alpha$. Utilice la Proposición 2.2.1 para mostrar que no$\triangle ABC$ es degenerado.