5.6: Círculos

Última actualización
Guardar como PDF

Page ID: 114833

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recordemos que un círculo con radio$r$ y centro$O$ es el conjunto de todos los puntos a la$r$ distancia de$O$. Decimos que un punto$P$ se encuentra dentro del círculo si$OP < r$; si$OP > r$, decimos que$P$ se encuentra fuera del círculo.

Ejercicio$\PageIndex{1}$

Dejar$\Gamma$ ser un círculo y$P \not\in \Gamma$. Supongamos que una línea$\ell$ está pasando por el punto$P$ y se cruza$\Gamma$ en dos puntos distintos,$X$ y$Y$. Demostrar que$P$ está dentro$\Gamma$ si y solo si$P$ yace entre$X$ y$Y$.

Pista

Que$O$ sea el centro del círculo. Tenga en cuenta que podemos asumir eso$O \ne P$.

Asumir$P$ mentiras entre$X$ y$Y$. Por el Ejercicio 5.1.1, podemos asumir que$OPX$ es correcto u obtuso. Por el Ejercicio 5.5.1,$OP < OX$; es decir,$P$ yace dentro$\Gamma$.

Si$P$ no se encuentra entre$X$ y$Y$, podemos suponer que$X$ se encuentra entre$P$ y$Y$. Ya que$OX = OY$, el Ejercicio 5.5.1 implica que$\angle OXY$ es agudo. Por lo tanto,$\angle OXP$ es obtuso. Aplicando el Ejercicio 5.5.1 otra vez conseguimos que$OP > OX$ l es decir,$P$ yace afuera$\Gamma$.

Un segmento entre dos puntos en un círculo se llama cuerda del círculo. Un acorde que pasa por el centro del círculo se llama su diámetro.

Ejercicio$\PageIndex{2}$

Asumir dos círculos distintos$\Gamma$ y$\Gamma'$ tener un acorde común$[AB]$. Mostrar que la línea entre centros de$\Gamma$ y$\Gamma'$ forma una bisectriz perpendicular a$[AB]$.

Pista: Aplicar Teorema 5.2.1.

Lema$\PageIndex{1}$

Una línea y un círculo pueden tener como máximo dos puntos de intersección.

Prueba

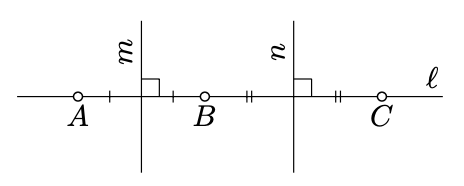
$2021-02-04 2.13.25.png$

Asumir$A, B$, y$C$ son puntos distintos que se encuentran en una línea$\ell$ y un círculo$\Gamma$ con el centro$O$. Entonces$OA = OB = OC$; en particular,$O$ se encuentra sobre los bisectores perpendiculares$m$ y$n$ hacia$[AB]$ y$[BC]$ respectivamente. Tenga en cuenta que los puntos medios de$[AB]$ y$[BC]$ son distintos. Por lo tanto,$m$ y$n$ son distintos. Lo contradice la singularidad de la perpendicular (Teorema 5.3.1).

Ejercicio$\PageIndex{3}$

Mostrar que dos círculos distintos pueden tener como máximo dos puntos de intersección.

Pista: Usar Ejercicio$\PageIndex{2}$ y Teorema 5.3.1.

En consecuencia del lema anterior, una línea$\ell$ y un círculo$\Gamma$ podrían tener 2, 1 o 0 puntos de intersecciones. En el primer caso la línea se llama línea secante, en el segundo caso es línea tangente; si$P$ es el único punto de intersección de$\ell$ y$\Gamma$, decimos que$\ell$ es tangente a$\Gamma$ at$P$.

De igual manera$\PageIndex{3}$, según Ejercicio, dos círculos distintos podrían tener 2, 1 o 0 puntos de intersecciones. Si$P$ es el único punto de intersección de círculos$\Gamma$ y$\Gamma'$, decimos que$\Gamma$ es tangente a$\Gamma$ at$P$; también asumimos que círculo es tangente a él mismo en cualquiera de sus puntos.

Lema$\PageIndex{2}$

Dejar$\ell$ ser una línea y$\Gamma$ ser un círculo con el centro$O$. Supongamos que$P$ es un punto común de$\ell$ y$\Gamma$. Entonces$\ell$ es tangente a$\Gamma$ a$P$ si y solo si$(PQ) \perp \ell$.

Prueba

Deja$Q$ ser el punto del pie de$O$ on$\ell$.

Asumir$P \ne Q$. Que$P'$ sea el reflejo de$P$ través$(OQ)$. Tenga en cuenta que$P' \in \ell$ y$(OQ)$ es la bisectriz perpendicular de$[PP']$. Por lo tanto,$OP = OP'$. De ahí$P, P' \in \Gamma \cap \ell$; es decir,$\ell$ es secante a$\Gamma$.

Si$P = Q$, entonces según Lemma 5.5.1,$OP < OX$ para cualquier punto$X \in \ell$ distinto de$P$. De ahí que$P$ sea el único punto en la intersección$\Gamma \cap \ell$; es decir,$\ell$ es tangente a$\Gamma$ at$P$.

Ejercicio$\PageIndex{4}$

Dejar$\Gamma$ y$\Gamma'$ ser dos círculos distintos con centros en$O$ y$O'$ respectivamente. Asumir$\Gamma$ se reúne$\Gamma'$ en el punto$P$. Mostrar que$\Gamma$ es tangente a$\Gamma'$ si y solo si$O$,$O'$, y$P$ se encuentran en una línea.

Pista: Que$P'$ sea el reflejo de$P$ través$(OO')$. Tenga en cuenta que$P'$ se encuentra en ambos círculos y$P' \ne P$ si y solo si$P \not\in (OO')$.

Ejercicio$\PageIndex{5}$

Dejar$\Gamma$ y$\Gamma'$ ser dos círculos distintos con centros en$O$$O'$ y y radios$r$ y$r'$. Mostrar que$\Gamma$ es tangente a$\Gamma'$ si y solo si

$OO' = r + r'$o$OO' = |r - r'|$.

Pista: Aplicar Ejercicio$\PageIndex{4}$

Ejercicio$\PageIndex{6}$

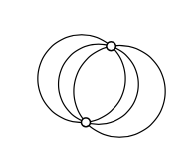
Supongamos que tres círculos tienen dos puntos en común. Demostrar que sus centros se encuentran en una línea.

$2021-02-04 2.31.06.png$

Pista: Dejar$A$ y$B$ ser los puntos de intersección. Tenga en cuenta que los centros se encuentran en la bisectriz perpendicular del segmento$[AB]$.

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Lema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{3}\)

Lema\(\PageIndex{2}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)