7.2: Reflexión a través de un punto

Última actualización
Guardar como PDF

Page ID: 114417

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Arreglar un punto$O$. Si$O$ es el punto medio de un segmento de línea$[XX']$, entonces decimos que$X'$ es un reflejo de$X$ a través del punto$O$.

Tenga en cuenta que el mapa$X \mapsto X'$ está definido de manera única; se llama reflexión a través$O$. En este caso$O$ se llama el centro de reflexión. Suponemos que$O' = O$; es decir,$O$ es un reflejo de sí mismo a través de sí mismo. Si la reflexión a través$O$ mueve un conjunto$S$ hacia sí mismo, entonces decimos que$S$ es centralmente simétrico con respecto a$O$.

Recordemos que cualquier movimiento es directo o indirecto; es decir, conserva o revierte los signos de los ángulos.

Proposición$\PageIndex{1}$

Cualquier reflexión a través de un punto es un movimiento directo.

Prueba

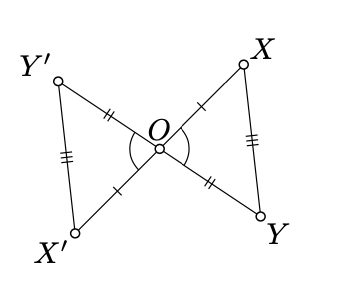
$2021-02-09 9.44.46.png$

Observe que si$X'$ es un reflejo de$X$ acroos$O$, entonces$X$ es un reflejo de$X'$. Es decir, la composición de la reflexión consigo misma es el mapa de identidad. En particular, cualquier reflexión a través de un punto es una biyección.

Fijar dos puntos$X$ y$Y$; dejar$X'$ y$Y'$ ser su reflejo a través$O$. Para comprobar que la reflexión es la preservación de la distancia, necesitamos demostrarlo$X'Y' = XY$.

Podemos suponer que$X, Y$ y$O$ son distintos; de lo contrario la afirmación es trivial. Por definición de reflexión a través$O$, tenemos eso$OX = OX'$,$OY = OY'$, y los ángulos$XOY$ y$X'OY'$ son verticales; en particular$\measuredangle XOY = \measuredangle X'OY'$. Por SAS,$\triangle XOY \cong \triangle X'OY'$; por lo tanto$X'Y' = XY$.

Por último, la reflexión a través$O$ no puede ser indirecta ya que$\measuredangle XOY = \measuredangle X'OY'$; por lo tanto, es un movimiento directo.

Ejercicio$\PageIndex{1}$

Supongamos$\angle AOB$ que tiene razón. Mostrar que la composición de reflexiones a través de las líneas$(OA)$ y$(OB)$ es un reflejo a través de$O$.

Utilice esta declaración y Corolario 5.4.1 para construir otra prueba de Proposición$\PageIndex{1}$.

Teorema$\PageIndex{1}$

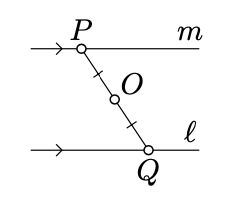
Dejar$\ell$ ser una línea,$Q \in \ell$, y$P$ es un punto arbitrario. Supongamos que$O$ es el punto medio de$[PQ]$. Entonces una línea$m$ que pasa a través$P$ es paralela a$\ell$ si y solo si$m$ es un reflejo de$\ell$ across$O$.

$2021-02-09 9.52.01.png$

Prueba

“si” parte. Supongamos que$m$ es un reflejo de$\ell$ a través$O$. Supongamos$\ell \nparallel m$; es decir$\ell$ e$m$ intersectar en un solo punto$Z$. Denotar por$Z'$ ser el reflejo de$Z$ través$O$.

$2021-02-09 9.53.35.png$

Tenga en cuenta que$Z'$ se encuentra en ambas líneas$\ell$ y$m$. De ello se deduce eso$Z' = Z$ o equivalentemente$Z = O$. En este caso$O \in \ell$ y por lo tanto el reflejo de lo$\ell$ ancho$O$ es en$\ell$ sí mismo; es decir,$\ell = m$ y en particular$\ell \parallel m$ —una contradicción.

“Solo si” parte. Que$\ell '$ sea el reflejo de$\ell$ través$O$. Según la parte “si” del teorema,$\ell ' \parallel \ell$. Tenga en cuenta que ambas líneas$\ell '$ y$m$ pasan a través$P$. Por singularidad de líneas paralelas (Teorema 7.1.1), si$m \parallel \ell$, entonces$\ell ' = m$; de donde sigue la declaración.

Proposición\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\)