7.1: Líneas paralelas
- Page ID
- 114407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
En consecuencia del Axioma II, cualesquiera dos líneas distintas\(\ell\) y\(m\) tienen un punto en común o ninguno. En el primer caso se cruzan (brevemente\(\ell \nparallel m\)); en el segundo caso, se dice que l y m son paralelos (brevemente,\(\ell \parallel m\)); además, una línea siempre se considera paralela a sí misma.
Para enfatizar que dos líneas en un diagrama son paralelas las marcaremos con flechas del mismo tipo.
Dejar\(\ell, m\), y\(n\) ser tres líneas. Supongamos que\(n \perp m\) y\(m \perp \ell\). Entonces\(\ell \parallel n\).
- Prueba
-
Asumir lo contrario; es decir,\(\ell \nparallel m\). Entonces hay un punto, digamos\(Z\), de intersección de\(\ell\) y\(n\). Entonces por el Teorema 5.3.1,\(\ell = n\). Como cualquier línea es paralela a sí misma, tenemos eso\(\ell \parallel n\) —una contradicción.
Para cualquier punto\(P\) y cualquier línea\(\ell\) hay una línea única\(m\) que pasa a través\(P\) y es paralela a\(\ell\).
El teorema anterior tiene dos partes, existencia y singularidad. En la prueba de singularidad utilizaremos el método de triángulos similares.
- Prueba
-
Aplicar el Teorema 5.3.1 dos veces, primero para construir la línea a\(n\) través\(P\) que es perpendicular a\(\ell\), y segundo para construir la línea a\(n\) través\(P\) que es perpendicular a\(m\). A continuación aplicar Proposición\(\PageIndex{1}\).
Singularidad. Si\(P \in \ell\), entonces\(m =\ell\) por la definición de líneas paralelas. Además asumimos\(P \not\in \ell\).
Construyamos las líneas\(n \ni P\) y\(m \ni P\) como en la prueba de existencia, así\(m \parallel \ell\).
Supongamos que hay otra línea\(s \ni P\) paralela a\(\ell\). Elija un punto\(Q \in s\) con el que se encuentra\(\ell\) en el mismo lado de\(m\). Deja\(R\) ser el punto del pie de\(Q\) on\(n\).
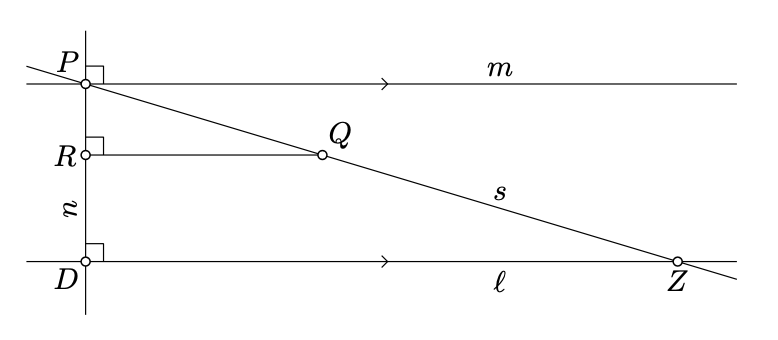
Dejar\(D\) ser el punto de intersección de\(n\) y\(\ell\). De acuerdo con la Proposición\(\PageIndex{1}\)\((QR) \parallel m\). Por lo tanto\(Q, R\),, y\(\ell\) se encuentran en el mismo lado de\(m\). En particular,\(R \in [PD)\).
Elija\(Z \in [PQ)\) tal que
\(\dfrac{PZ}{PQ} = \dfrac{PD}{PR}.\)
Por condición de similitud SAS (o equivalentemente por Axioma V) tenemos eso\(\triangle RPQ \sim \triangle DPZ\); por lo tanto\((ZD) \perp (PD)\). De ello se deduce que\(Z\) yace sobre\(\ell\) y\(s\) - una condición.
Asumir\(\ell, m\), y\(n\) son líneas tales que\(\ell \parallel m\) y\(m \parallel n\). Entonces\(\ell \parallel n\).
- Prueba
-
Asumir lo contrario; es decir,\(\ell \nparallel n\). Entonces hay un punto\(P \in \ell \cap n\). Por teorema\(\PageIndex{1}\),\(n = \ell\) — una contradicción.
Tenga en cuenta que a partir de la definición, tenemos eso\(\ell \parallel m\) si y solo si\(m \parallel \ell\). Por lo tanto, según el corolario anterior, "\(\parallel\)" es una relación de equivalencia. Es decir, para cualquier línea\(\ell, m\), y\(n\) se mantienen las siguientes condiciones:
(i)\(\ell \parallel \ell\);
(ii) si\(\ell \parallel m\), entonces\(m \parallel \ell\);
(iii) si\(\ell \parallel m\) y\(m \parallel n\), entonces\(\ell \parallel n\).
Dejar\(k, \ell, m\), y\(n\) ser líneas tales que\(k \perp \ell\),\(\ell \perp m\), y\(m \perp n\). \(k \nparallel n\)Demuéstralo.
- Pista
-
Aplicar Proposición\(\PageIndex{1}\) para demostrarlo\(k \parallel m\). Por Corolario\(\PageIndex{2}\),\(k \parallel n \Rightarrow m \parallel n\). Esto último contradice eso\(m \perp n\).
Haga una construcción de regla y brújula de una línea a través de un punto dado que sea paralelo a una línea dada.
- Pista
-
Repita la construcción en el Ejercicio 5.7.1 dos veces.