7.6: Método de coordenadas

Última actualización
Guardar como PDF

Page ID: 114398

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El siguiente ejercicio es importante; demuestra que nuestra definición axiomática concuerda con la definición del modelo.

Ejercicio$\PageIndex{1}$

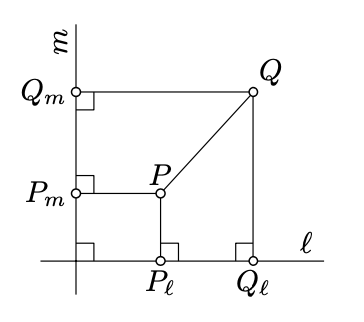
$2021-02-11 11.29.32.png$

Dejar$\ell$ y$m$ ser líneas perpendiculares en el plano euclidiano. Dado un punto$P$, vamos$P_{\ell}$ y$P_m$ denotan los puntos del pie de$P$ on$\ell$ y$m$ respectivamente.

Demostrar que para cualquier$X \in \ell$ y$Y \in m$ hay un punto único$P$ tal que$P_{\ell} = X$ y$P_m = Y$.
Demuestre eso$PQ^2 = P_{\ell}Q_{\ell}^2 + P_m Q_m^2$ para cualquier par de puntos$P$ y$Q$.
Concluir que el plano es isométrico a$(\mathbb{R}^2, d_2)$.

Pista

(a). Utilizar la singularidad de la línea paralela (Teorema 7.1.1).

b). Usa Lema 7.5.1 y el teorema de Pitágoras (Teorema 6.2.1)

Una vez resuelto este ejercicio, podemos aplicar el método de coordenadas para resolver cualquier problema en la geometría del plano euclidiano. Este método es poderoso y universal; se desarrollará más en el Capítulo 18.

Ejercicio$\PageIndex{2}$

Utilizar el Ejercicio$\PageIndex{1}$ para dar una prueba alternativa del Teorema 3.5.1 en el plano euclídeo.

Es decir, probar que dados los números reales$a, b$, y$c$ tal que

$0 < a \le b \le c \le a + b$,

hay un triángulo$ABC$ tal que$a = BC$,$b = CA$, y$c = AB$.

Pista

Establecer$A = (0, 0), B = (c, 0)$, y$C = (x, y)$. Claramente,$AB = c$,$AC^2 = x^2 + y^2$ y$BC^2 = (c - x)^2 + y^2$.

Queda por demostrar que existe un par de números reales$(x, y)$ que satisfagan el siguiente sistema de ecuaciones:

$\begin{cases} b^2 = x^2 + y^2 \\ a^2 = (c- x)^2 + y^2 \end{cases}$

si$0 < a \le b \le c \le a + c$.

Ejercicio$\PageIndex{3}$

Considera dos puntos distintos$A = (x_A, y_A)$ y$B = (x_B, y_B)$ en el plano de coordenadas. Mostrar que la bisectriz perpendicular a$[AB]$ es descrita por la ecuación

$2 \cdot (x_B - x_A) \cdot x + 2 \cdot (y_B - y_A) \cdot y = x_B^2 + y_B^2 - x_A^2 - y_B^2$.

Concluye que la línea se puede definir como un subconjunto del plano de coordenadas del siguiente tipo:

Soluciones de una ecuación$a \cdot x + b \cdot y = c$ para algunas constantes$a, b$, y$c$ tal que$a \ne 0$ o$b \ne 0$.
El conjunto de puntos$(a \cdot t + c, b \cdot t + d)$ para algunas constantes$a, b, c$, y$d$ tal que$a \ne 0$ o$b \ne 0$ y todos$t \in \mathbb{R}$.

Pista

Tenga en cuenta que$MA = MB$ si y solo si

$(x - x_A)^2 + (y - y_A)^2 = (x - x_B)^2 + (y - y_B)^2$

donde$M = (x, y)$. Para probar la primera parte, simplificar esta ecuación. Para las piezas restantes, use que cualquier línea sea una bisectriz perpendicular a algún segmento de línea.

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)