4.4: Teorema de Pitágoras
- Page ID
- 114626
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
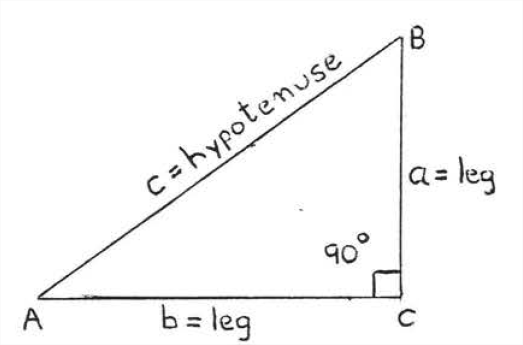
En un triángulo rectángulo, los lados del ángulo recto se llaman las patas del triángulo y el lado restante se llama hipotenusa. En Figura\(\PageIndex{1}\), lado\(AC\) y\(BC\) son las piernas y lado\(AB\) es la hipotenusa.
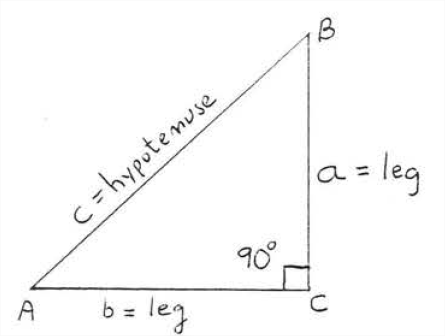
El siguiente es uno de los teoremas más famosos de las matemáticas.
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. Es decir,
\[\text{leg}^{2}+\text{leg}^{2}=\text{hypotenuse}^{2}\]
Así, para los lados del triángulo en la Figura\(\PageIndex{1}\),
\[a^{2}+b^{2}=c^{2} \nonumber\]
Antes de probar el Teorema\(\PageIndex{1}\), daremos varios ejemplos.
Encuentra\(x\)
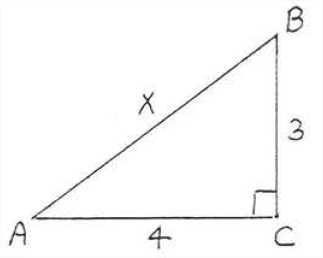
Solución
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {3^2 + 4^2} & = & {x^2} \\ {9 + 16} & = & {x^2} \\ {25} & = & {x^2} \\ {5} & = & {x} \end{array}\)
Comprobar:
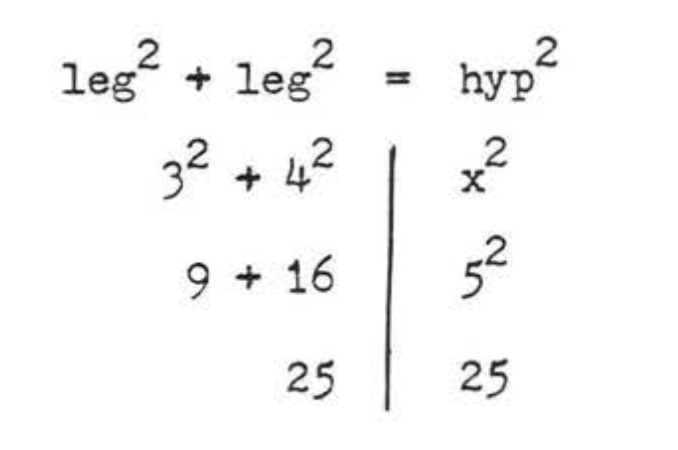
Respuesta:\(x = 5\).
Encuentra\(x\):
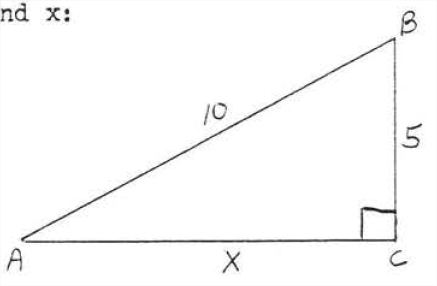
Solución
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {5^2 + x^2} & = & {10^2} \\ {25 + x^2} & = & {100} \\ {x^2} & = & {75} \\ {x} & = & {\sqrt{75} = \sqrt{25} \sqrt{3} = 5\sqrt{3}} \end{array}\)
Comprobar:
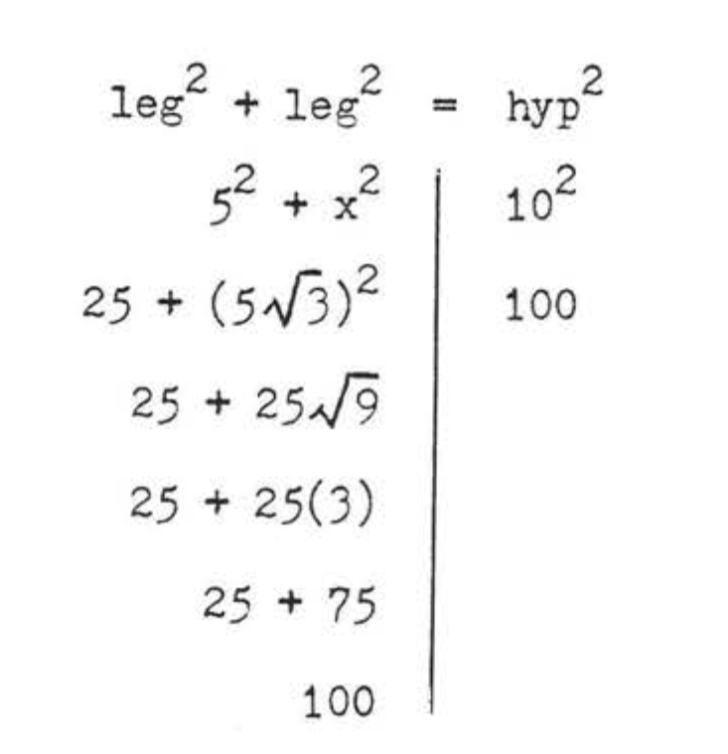
Respuesta:\(x = 5\sqrt{3}\).
Encuentra\(x\):
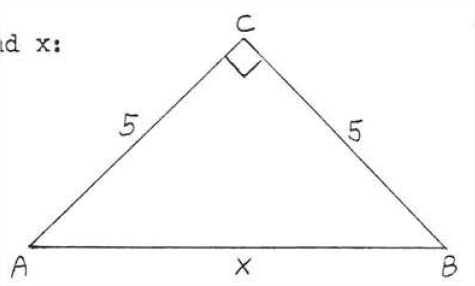
Solución
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {5^2 + 5^2} & = & {x^2} \\ {25 + 25} & = & {x^2} \\ {50} & = & {x^2} \\ {x} & = & {\sqrt{50} = \sqrt{25} \sqrt{2} = 5\sqrt{2}} \end{array}\)
Comprobar:
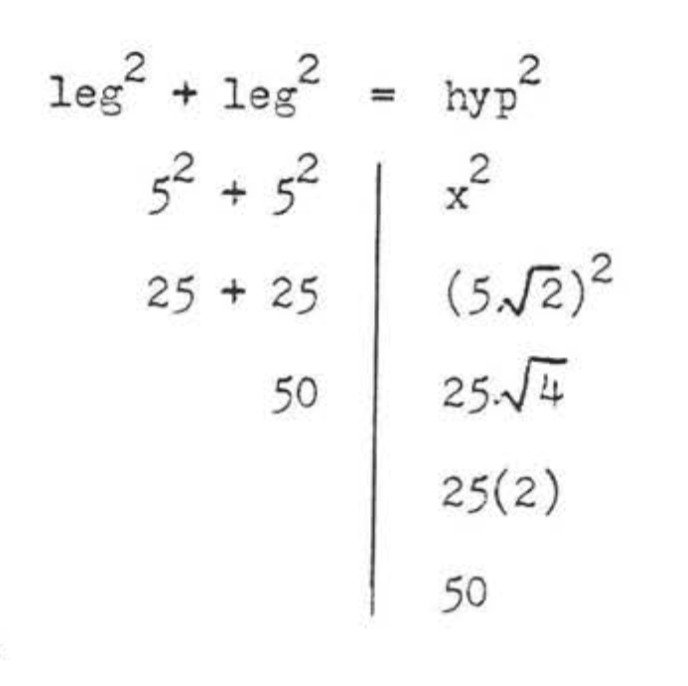
Respuesta:\(x = 5\sqrt{2}\).
Encuentra\(x\)
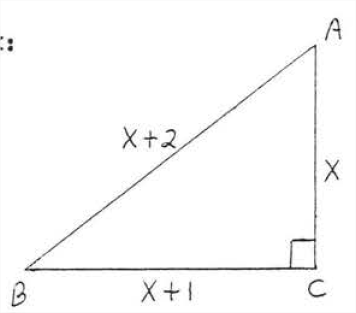
Solución
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {x^2 + (x + 1)^2} & = & {(x + 2)^2} \\ {x^2 + x^2 + 2x + 1} & = & {x^2 + 4x + 4} \\ {x^2 + x^2 + 2x + 1 - x^2 - 4x - 4} & = & {0} \\ {x^2 - 2x - 3} & = & {0} \\ {(x - 3)(x + 1)} & = & {0} \end{array}\)
\(\begin{array} {rcl} {x - 3} & = & {0} \\ {x} & = & {3} \end{array}\)\(\begin{array} {rcl} {x + 1} & = & {0} \\ {x} & = & {-1} \end{array}\)
Rechazamos\(x = -1\) porque\(AC = x\) no puede ser negativo.
Comprobar,\(x = 3\):
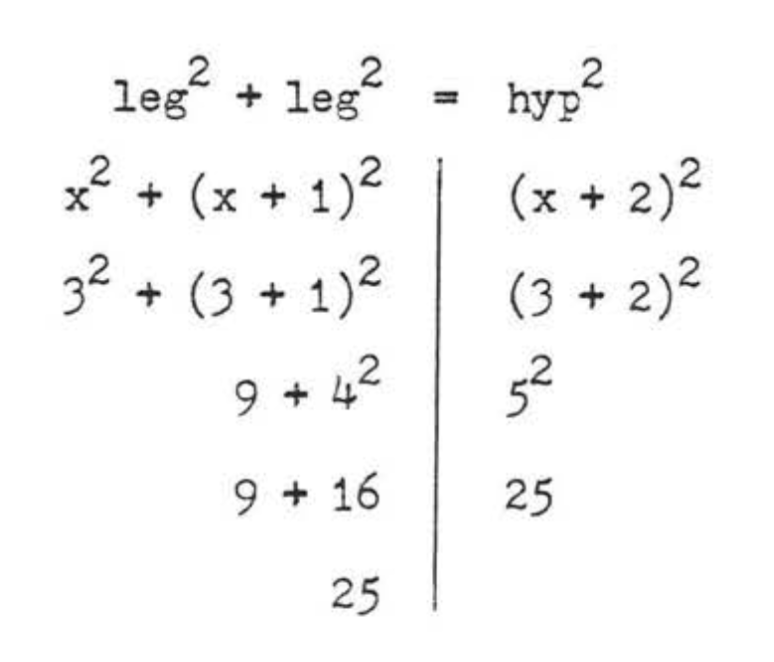
Respuesta:\(x = 3\).
Ahora vamos a reafirmar y probar Teorema\(\PageIndex{1}\):
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. Es decir,
\(\text{leg}^2 + \text{leg}^2 = \text{hypotenuse}^2.\)
En la Figura\(\PageIndex{1}\),
\(a^2 + b^2 = c^2.\)

- Prueba
-
En la Figura\(\PageIndex{1}\), draw \(CD\) perpendicular to \(AB\). Let \(x = AD\). Then \(BD = c - x\) (Figure \(\PageIndex{2}\)). As in Example \(\PageIndex{3}\), section 4.2, \(\triangle ABC \sim \triangle ACD\) and \(\triangle ABC \sim \triangle CBD\). From these two similarities we obtain two proportions:

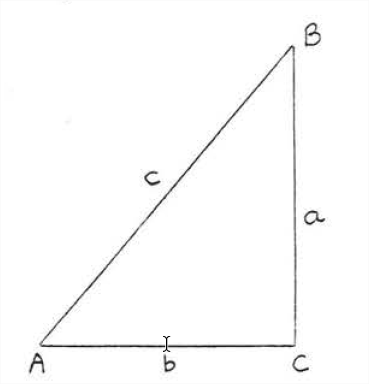
Lo contrario del Teorema de Pitágoras también sostiene:
In a triangle, if the square of one side is equal to the sun of the squares of the other two sides then the triangle is a right triangle.
In Figure \(\PageIndex{3}\), if \(c^2 = a^2 + b^2\) then \(\triangle ABC\) is a right triangle with \(\angle C = 90^{\circ}\).
- Proof
-
Draw a new triangle, \(\triangle DEF\), so that \(\angle F = 90^{\circ}\), \(d = a\), and \(e = b\) (Figure \(\PageIndex{4}\)). \(\triangle DEF\) is a right triangle, so by Theorem \(\PageIndex{1}\), \(f^2 = d^2 + e^2\). We have \(f^2 = d^2 + e^2 = a^2 + b^2 = c^2\) and therefore \(f = c\). Therefore \(\triangle ABC \cong \triangle DEF\) because \(SSS = SSS\). Therefore, \(\angle C + \angle F = 90^{\circ}\).

Figure \(\PageIndex{4}\): Given \(\triangle ABC\), draw \(\triangle DEF\) so that \(\angle F = 90^{\circ}\), \(d = a\) and \(e = b\).
Is \(\triangle ABC\) a right triangle?

Solution
\(\text{AC}^2 = 7^2 = 49\)
\(\text{BC}^2 = 9^2 = 81\)
\(\text{AB}^2 = (\sqrt{130})^2 = 130\)
\(49 + 81 = 130\).
so by Theorem \(\PageIndex{2}\), \(\triangle ABC\) is a right triangle.
Answer: yes.
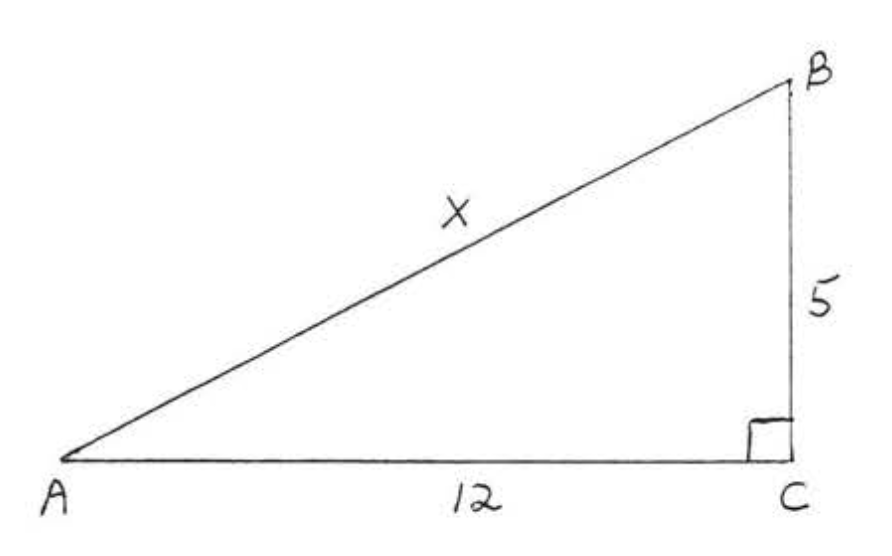
Find \(x\) and \(AB\):
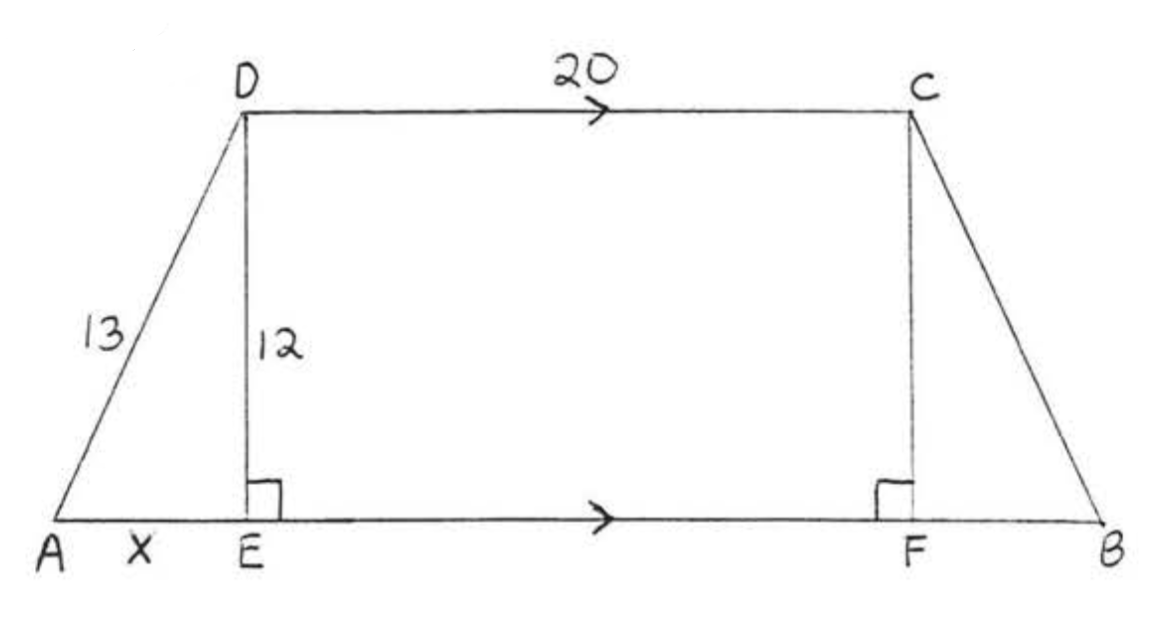
Solution
\(\begin{array} {rcl} {x^2 + 12^2} & = & {13^2} \\ {x^2 + 144} & = & {169} \\ {x^2} & = & {169 - 144} \\ {x^2} & = & {25} \\ {x} & = & {5} \end{array}\)
\(CDEF\) is a rectangle so \(EF = CD = 20\) and \(CF = DE = 12\). Therefore \(FB = 5\) and \(AB = AE + EF + FB = 5 + 20 + 5 = 30\).
Answer: \(x = 5\), \(AB = 30\).
Find \(x\), \(AC\) and \(BD\):
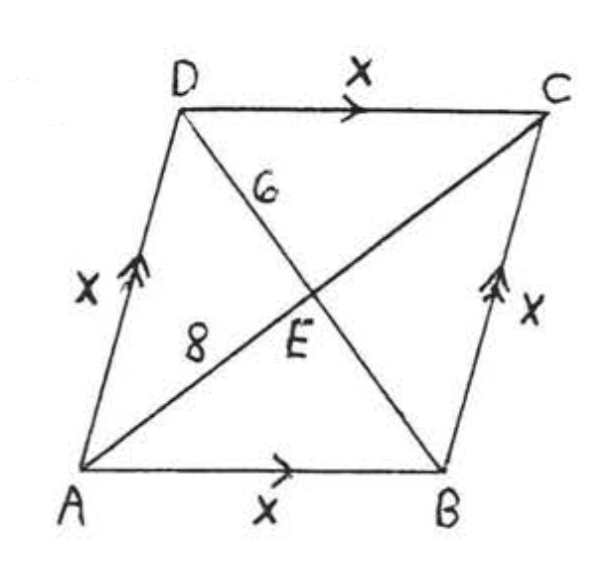
Solution
\(ABCD\) is a rhombus. The diagonals of a rhombus are perpendicular and bisect each other.
\(\begin{array} {rcl} {6^2 + 8^2} & = & {x^2} \\ {36 + 64} & = & {x^2} \\ {100} & = & {x^2} \\ {10} & = & {x} \end{array}\)
\(AC = 8 + 8 = 16, BD = 6 + 6 = 12.\)
Answer: \(x = 10, AC = 16, BD = 12\).
A ladder 39 feet long leans against a building, How far up the side of the building does the ladder reach if the foot of the ladder is 15 feet from the building?

Solution
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {x^2 + 15^2} & = & {39^2} \\ {x^2 + 225} & = & {1521} \\ {x^2} & = & {1521 - 225} \\ {x^2} & = & {1296} \\ {x} & = & {\sqrt{1296} = 36} \end{array}\)
Answer: 36 feet.
Pythagoras (c. 582 - 507 B.C.) was not the first to discover the theorem which bears his name. It was known long before his time by the Chinese, the Babylonians, and perhaps also the Egyptians and the Hindus, According to tradition, Pythagoras was the first to give a nroof of the theorem, His proof probably made use of areas, like the one suggested. In Figure \(\PageIndex{5}\) below, (each square contains four congruent right triangles with sides of lengths \(a\), \(b\), and \(c\), In addition the square on the left contains a square with side a and a square with side \(b\) while the one on the right contains a square with side c.)
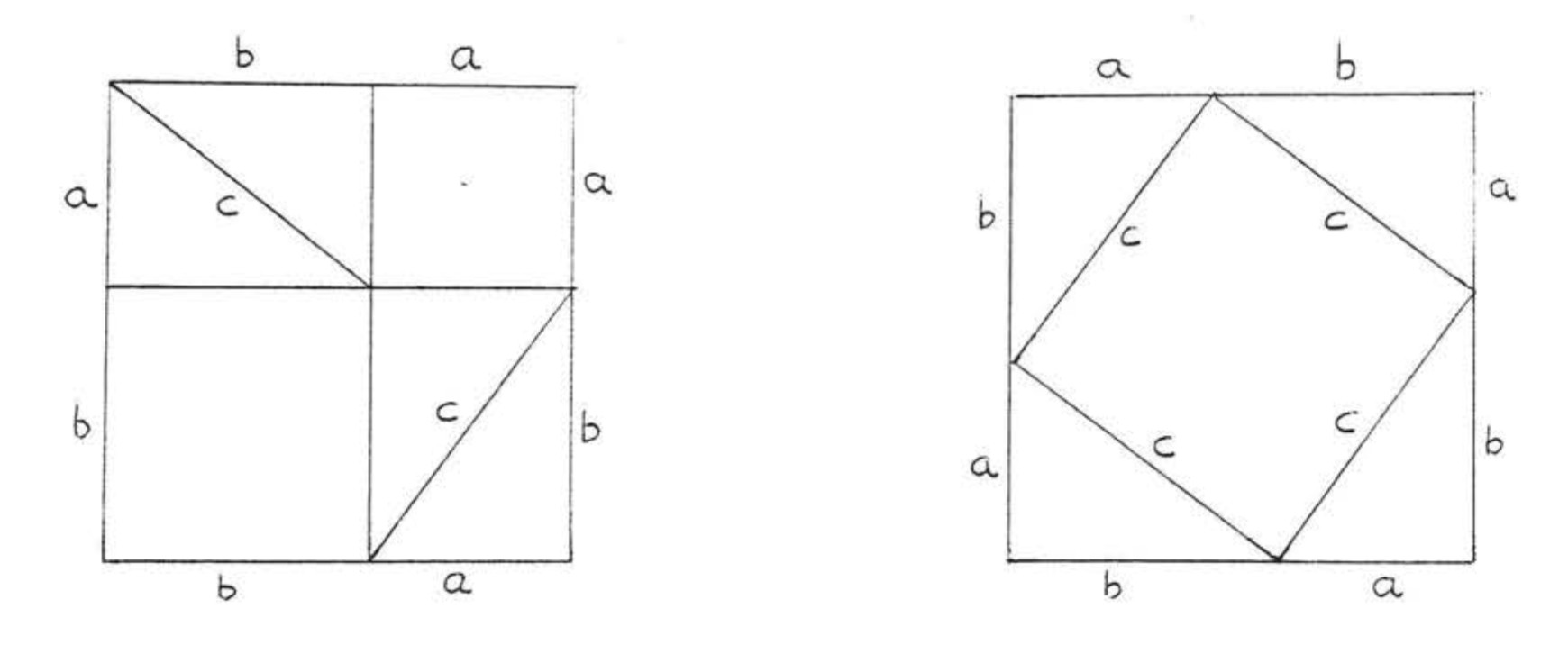
um theorem for triangles, the properties of parallel lines, and the theory of similar triangles and proportions.
Problems
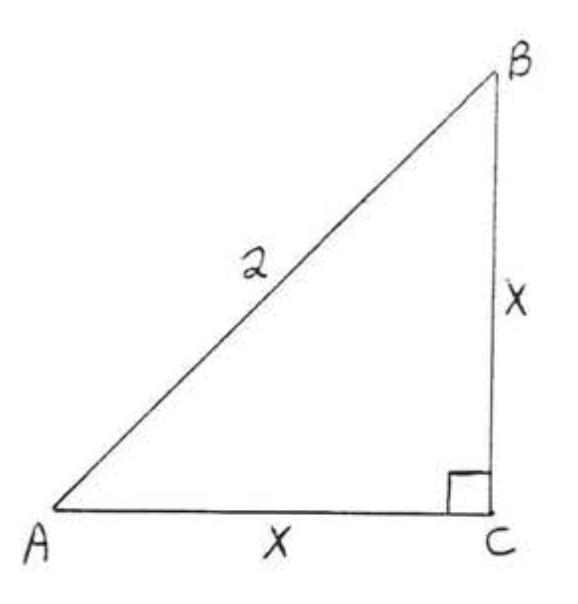
1 - 10. Find \(x\). Leave answers in simplest radical form.
1.

2.
3.

4.

5.

6.
7.

8.

9.

10.

11 - 14. Find \(x\) and all sides of the triangle:
11.

12.

13.
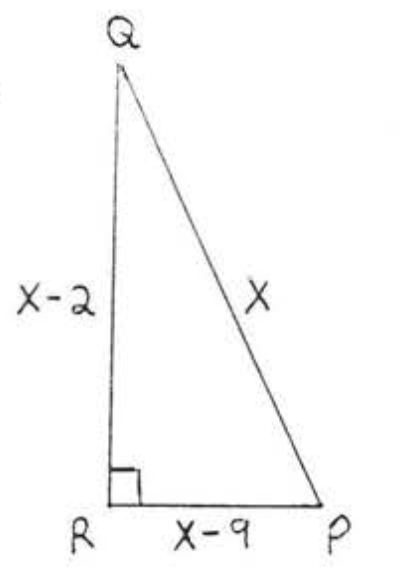
14.

15 - 16. Find \(x\):
15.

16.

17. Find \(x\) and \(AB\).

18. Find \(x\):

19. Find \(x, AC\) and \(BD\):

20. Find \(x, AC\) and \(BD\):

21. Find \(x\) and \(y\):

22. Find \(x\), \(AC\) and \(BD\):

23. Find \(x, AB\) and \(BD\):
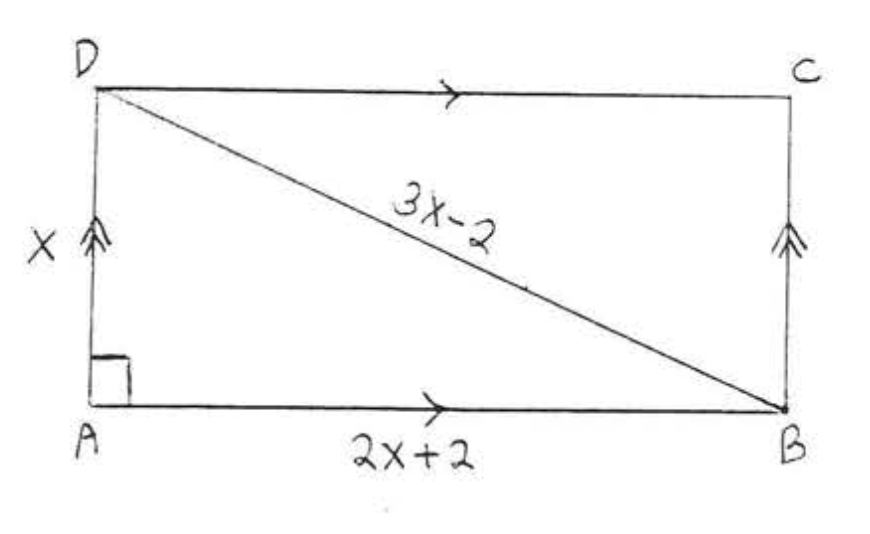
24. Find \(x, AB\) and \(AD\):

25 - 30. Is \(\triangle ABC\) a right triangle?
25.

26.
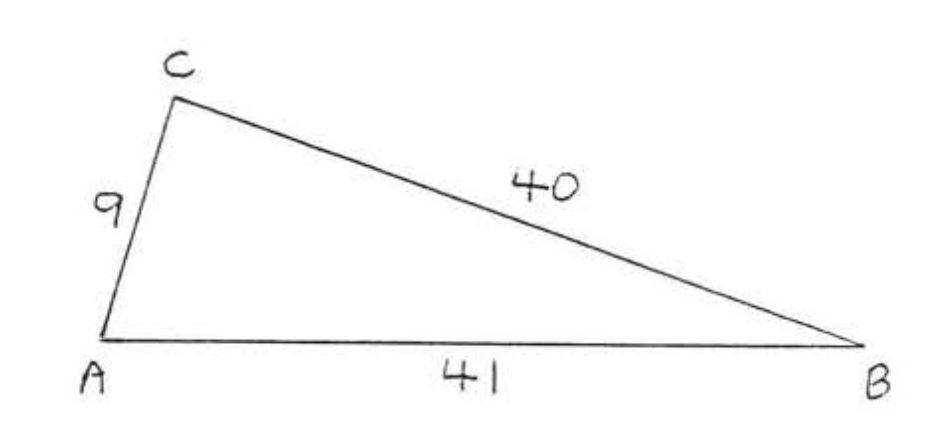
27.
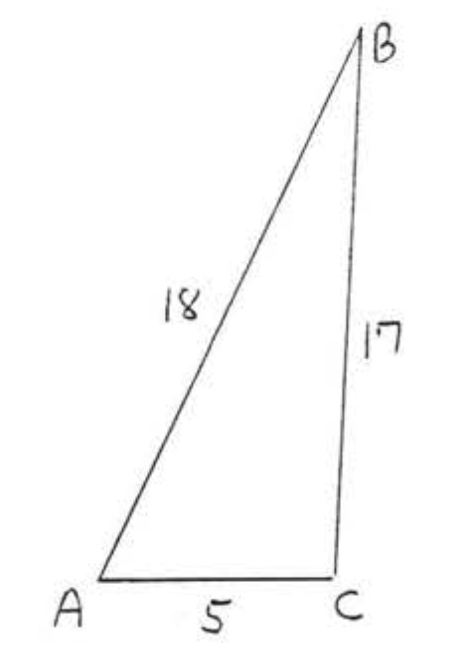
28.
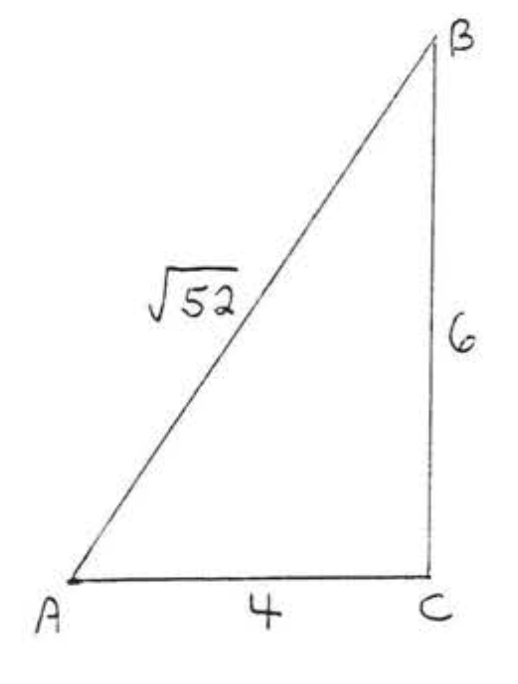
29.

30.

31. A ladder 25 feet long leans against a building, How far up the side of the building does the ladder reach if the foot of the ladder is 7 feet from the building?
32. A man travels 24 miles east and then 10 miles north. At the end of his journey how far is he from his starting point?
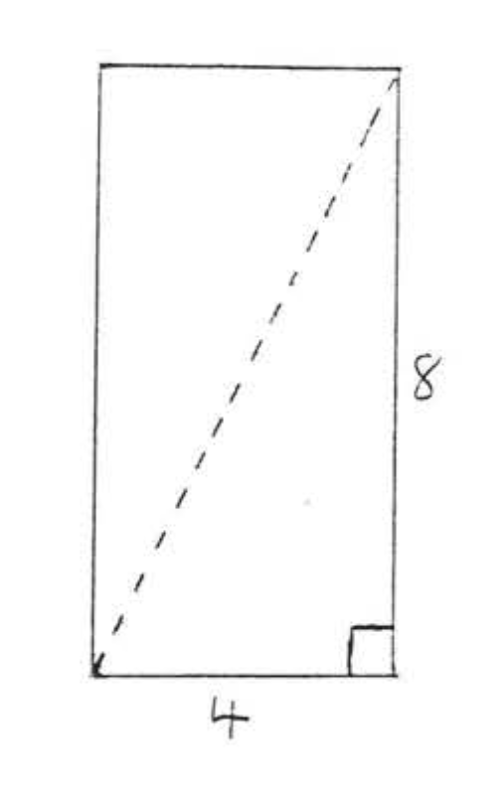
33. Can a table 9 feet wide (with its legs folded) fit through a rectangular doorway 4 feet by 8 feet?
34. A baseball diamond is a square 90 feet on each side, Find the distance from home plate to second base (leave answer in simplest radical form).



