1.1: Una introducción a los límites
- Page ID
- 111882
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comenzamos nuestro estudio de límites considerando ejemplos que demuestran conceptos clave que se explicarán a medida que avanzamos.
Considera la función\(y = \frac{\sin x}{x}\). ¿Cuándo\(x\) está cerca del valor 1, qué valor (si lo hay) está\(y\) cerca?
Si bien nuestra pregunta no se forma con precisión (¿qué constituye “cerca del valor 1"?) , la respuesta no parece difícil de encontrar. Uno podría pensar primero en mirar una gráfica de esta función para aproximar\(y\) los valores apropiados.
Considere la Figura 1, donde\(y = \frac{\sin x}{x}\) se grafica. Para valores\(x\) cercanos a 1, parece que\(y\) toma valores cercanos\(0.85\). De hecho, cuando\(x=1\), entonces\(y=\frac{\sin 1}{1} \approx 0.84\), así tiene sentido que cuando\(x\) está “cerca” 1,\(y\) será “cerca”\(0.84\).
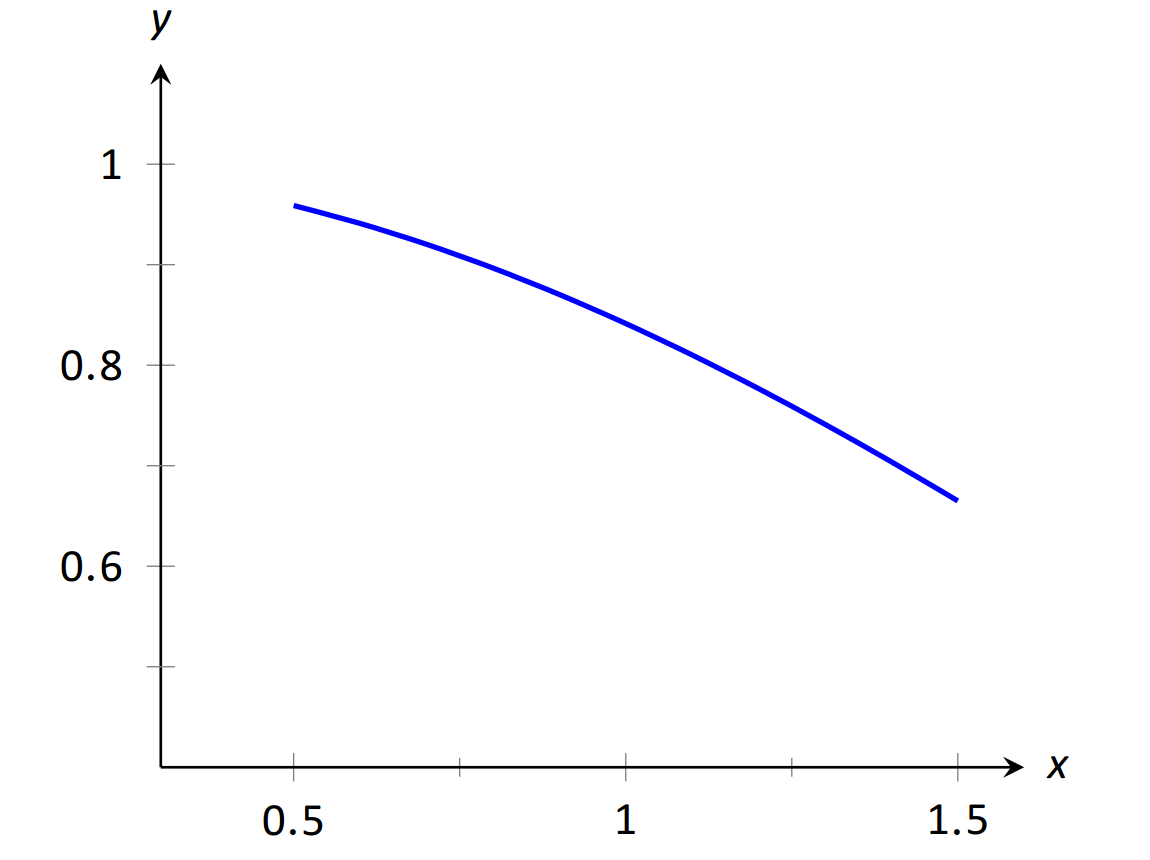
\(\text{FIGURE 1.1}\):\(\sin (x)/x \text{ near }x=1.\)
Considera esto nuevamente a un valor diferente para\(x\). ¿Cuándo\(x\) está cerca de 0, qué valor (si lo hay) está\(y\) cerca? Al considerar la Figura 1.2, se puede ver que parece que\(y\) toma valores cercanos\(1\). Pero, ¿qué pasa cuando\(x=0\)? Tenemos
\[y \rightarrow \frac{\sin 0}{0}\rightarrow "\frac{0}{0}".\nonumber\]
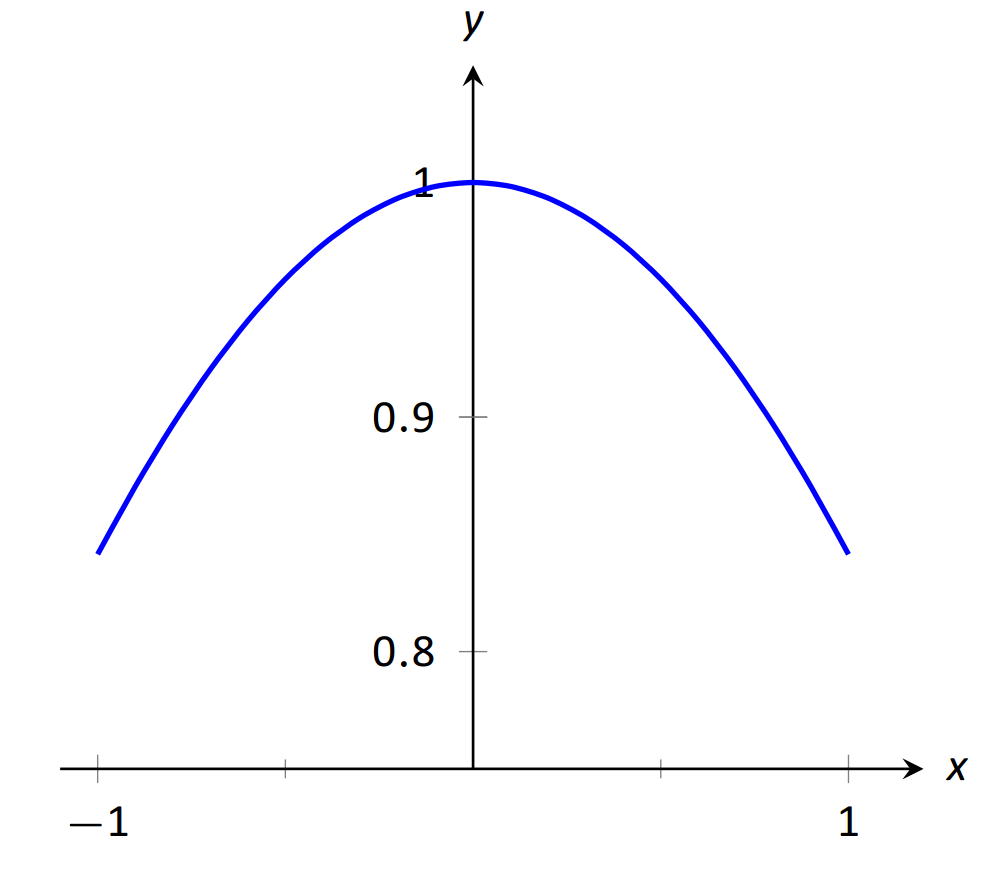
\(\text{FIGURE 1.2}\):\(\sin (x)/x \text{ near }x=0.\)
La expresión\(0/0\) "" no tiene valor; es indeterminada. Tal expresión no da información sobre lo que está pasando con la función cercana. No podemos averiguar cómo\(y\) se comporta cerca\(x=0\) para esta función simplemente dejando\(x=0\).
Encontrar un límite implica comprender cómo se comporta una función cerca de un valor particular de\(x\). Antes de continuar, será útil establecer alguna notación. Dejar\(y=f(x)\); es decir, dejar\(y\) ser una función de\(x\) para alguna función\(f\). La expresión “el límite de\(y\) como\(x\) se acerca a 1" describe un número, a menudo referido como\(L\), que se\(y\) acerca como se\(x\) acerca a 1. Escribimos todo esto como
\[\lim_{x\to 1} y = \lim_{x\to 1} f(x) = L.\nonumber\]
Esta no es una definición completa (que vendrá en la siguiente sección); se trata de una pseudo-definición que nos permitirá explorar la idea de un límite.
Arriba, donde\(f(x) = \sin(x)/x\), aproximamos
\[\lim_{x\to 1} \frac{\sin x}{x} \approx 0.84 \quad \text{ and } \quad \lim_{x\to 0}\frac{\sin x}{x} \approx 1.\nonumber\]
(Aproximamos estos límites, de ahí que usemos el símbolo\(\approx\) ""”, ya que estamos trabajando con la pseudo-definición de un límite, no con la definición real.)
Una vez que tengamos la verdadera definición de un límite, encontraremos límites analíticamente; es decir, usando exactamente una variedad de herramientas matemáticas. Por ahora, aproximaremos límites tanto gráfica como numéricamente. Graficar una función puede proporcionar una buena aproximación, aunque a menudo no es muy precisa. Los métodos numéricos pueden proporcionar una aproximación más precisa. Ya hemos aproximado los límites gráficamente, por lo que ahora volvemos nuestra atención a las aproximaciones numéricas.
Considerar de nuevo\(\lim_{x\to 1}\sin (x)/x\). Para aproximar este límite numéricamente, podemos crear una tabla de\(x\) y\(f(x)\) valores donde\(x\) está “cerca” 1. Esto se hace en la Figura 1.3.
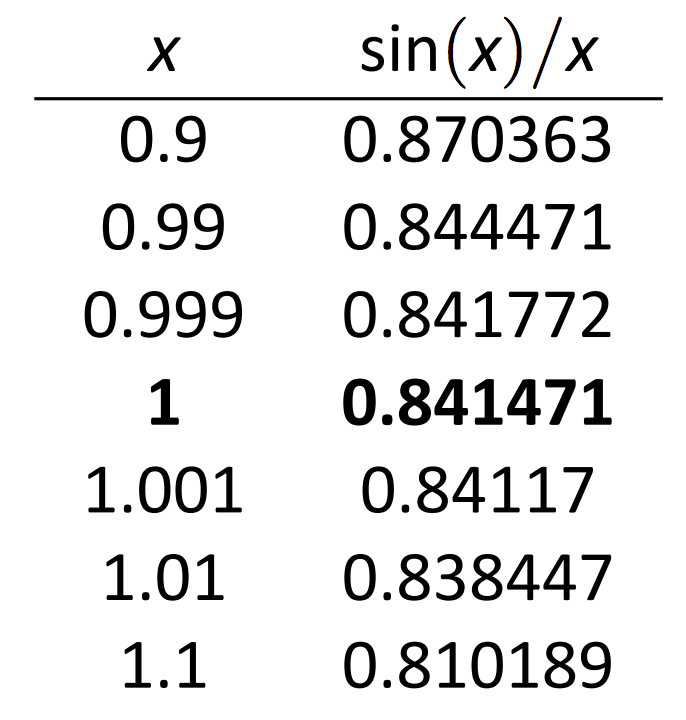
\(\text{FIGURE 1.3}\): Valores de\(\sin (x)/x \text{ with }x \text{ near }1.\)
Observe que para valores de\(x\) cerca\(1\), tenemos\(\sin (x)/x\) cerca\(0.841\). La\(x=1\) fila está en negrita para resaltar el hecho de que al considerar límites, no nos preocupa el valor de la función en ese\(x\) valor particular; solo nos preocupan los valores de la función cuando\(x\) está cerca de 1.
Ahora aproximado\(\lim_{x\to 0} \sin(x)/x\) numéricamente. Ya aproximamos el valor de este límite como 1 gráficamente en la Figura 1.2. El cuadro de la Figura 1.4 muestra el valor de\(\sin(x)/x\) para valores\(x\) cercanos a 0. Se muestran diez lugares después del punto decimal para resaltar qué tan cerca de 1 el valor de\(\sin(x)/x\) obtiene como\(x\) toma valores muy cercanos a 0. Incluimos la\(x=0\) fila en negrita nuevamente para enfatizar que no nos preocupa el valor de nuestra función at\(x=0\), solo en el comportamiento de la función cerca de 0.
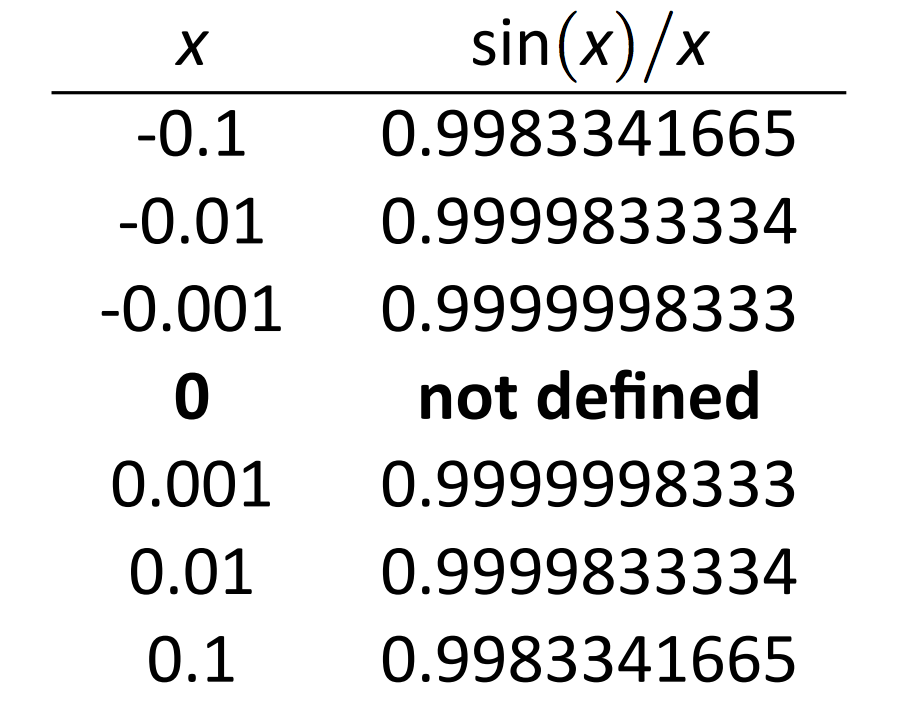
\(\text{FIGURE 1.4}\): Valores de\(\sin (x)/x \text{ with }x \text{ near }1.\)
Este método numérico da confianza para decir que 1 es una buena aproximación de\(\lim_{x\to 0} \sin(x)/x\); es decir,
\[\lim_{x\to 0} \sin(x)/x \approx 1.\]
Posteriormente podremos demostrar que el límite es exactamente 1.
Consideramos ahora varios ejemplos que nos permiten explorar diferentes aspectos del concepto límite.
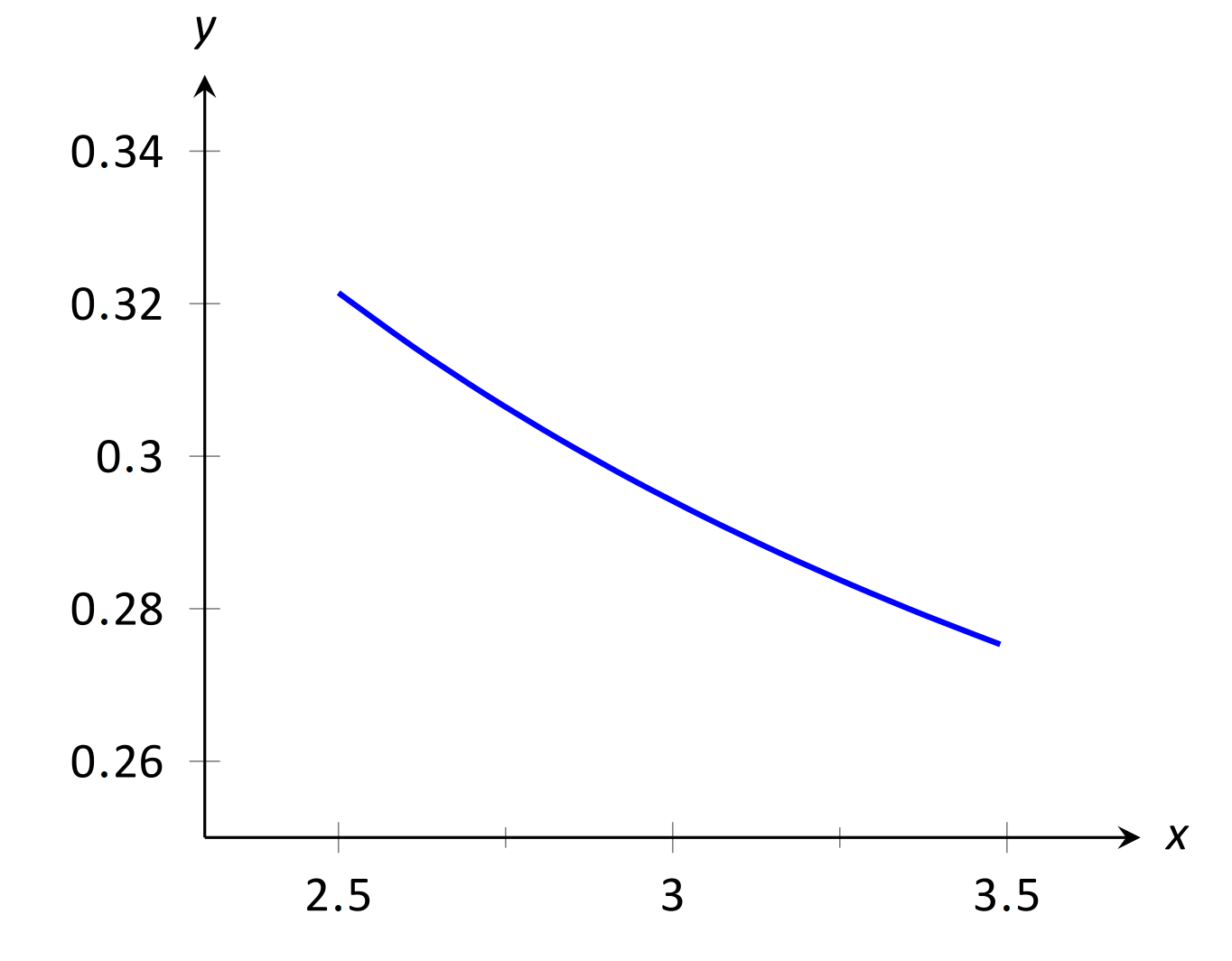
\(\text{FIGURE 1.5}\): Aproximando gráficamente un límite en el Ejemplo 1.
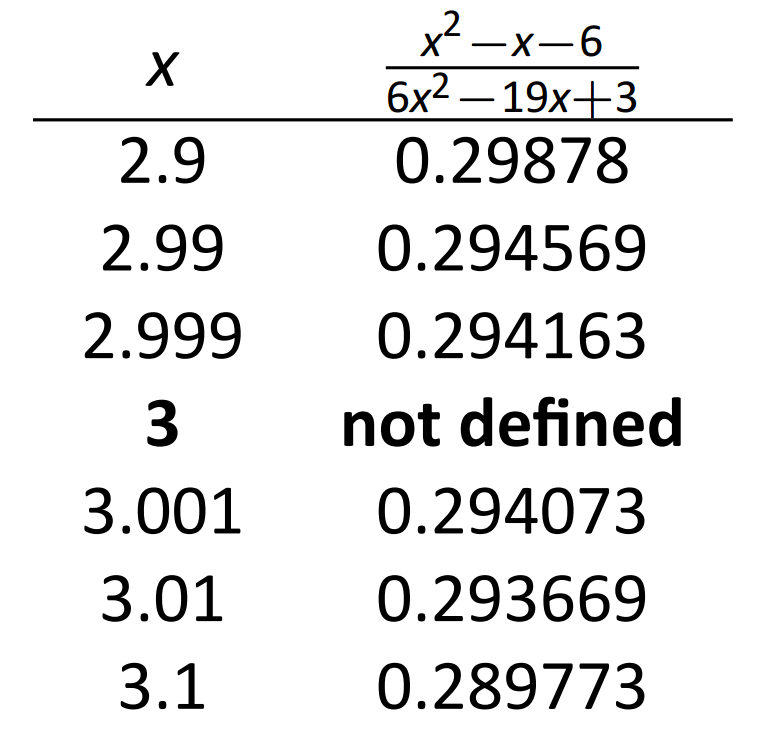
\(\text{FIGURE 1.6}\): Aproximando numéricamente un límite en el Ejemplo 1.
Ejemplo 1: Aproximación al valor de un límite
Utilizar métodos gráficos y numéricos para aproximar
\[\lim_{x\to 3} \frac{x^2-x-6}{6x^2-19x+3}.\]
Solución:
Para aproximar gráficamente el límite, graficar
\[y = (x^2-x-6)/(6x^2-19x+3)\]
en un pequeño intervalo que contiene 3. Para aproximar numéricamente el límite, cree una tabla de valores donde los\(x\) valores estén cerca de 3. Esto se hace en las Figuras 1.5 y 1.6, respectivamente.
La gráfica muestra que cuando\(x\) está cerca de 3, el valor de\(y\) está muy cerca\(0.3\). Al considerar valores\(x\) cercanos a 3, vemos que\(y=0.294\) es una mejor aproximación. La gráfica y la tabla implican que
\[\lim_{x\to 3} \frac{x^2-x-6}{6x^2-19x+3} \approx 0.294.\]
Este ejemplo puede plantear algunas preguntas sobre la aproximación de los límites (y la naturaleza de los propios límites).
- Si una gráfica no produce una aproximación tan buena como una tabla, ¿por qué molestarse con ella?
- ¿Cuántos valores de\(x\) en una tabla son “suficientes”? En el ejemplo anterior, ¿podríamos haber usado\(x=3.001\) y encontrado una aproximación fina?
Las gráficas son útiles ya que dan una comprensión visual sobre el comportamiento de una función. A veces una función puede actuar “erráticamente” cerca de ciertos\(x\) valores que es difícil de discernir numéricamente pero muy simple gráficamente. Dado que las utilidades gráficas son muy accesibles, tiene sentido hacer un uso adecuado de ellas.
Dado que las tablas y gráficas se utilizan únicamente para aproximar el valor de un límite, no hay una respuesta firme a cuántos puntos de datos son “suficientes”. Incluir lo suficiente para que una tendencia sea clara, y utilizar valores (cuando sea posible) tanto menores como mayores que el valor en cuestión. En el Ejemplo 1, se utilizaron ambos valores menores que y mayores que 3. Si hubiéramos usado solo\(x=3.001\), podríamos haber tenido la tentación de concluir que el límite tenía un valor de\(0.3\). Si bien esto no está lejos, podríamos hacerlo mejor. El uso de valores “en ambos lados del 3" nos ayuda a identificar tendencias.
Ejemplo 2: Aproximación al valor de un límite
Aproximar gráfica y numéricamente el límite de\(f(x)\) como se\(x\) acerca a 0, donde
\[f(x) = \left \{\begin{array}{rl} x+1 & x< 0 \\ -x^2+1 & x > 0 \end{array}\right . \]
Solución:
Nuevamente graficamos\(f(x)\) y creamos una tabla de sus valores cerca\(x=0\) para aproximarse al límite. Tenga en cuenta que esta es una función definida por partes, por lo que se comporta de manera diferente a cada lado de 0. La Figura 1.7 muestra una gráfica de\(f(x)\), y a cada lado de 0 parece que los\(y\) valores se acercan a 1. Tenga en cuenta que en realidad no\(f(0)\) se define, como se indica en la gráfica con el círculo abierto.
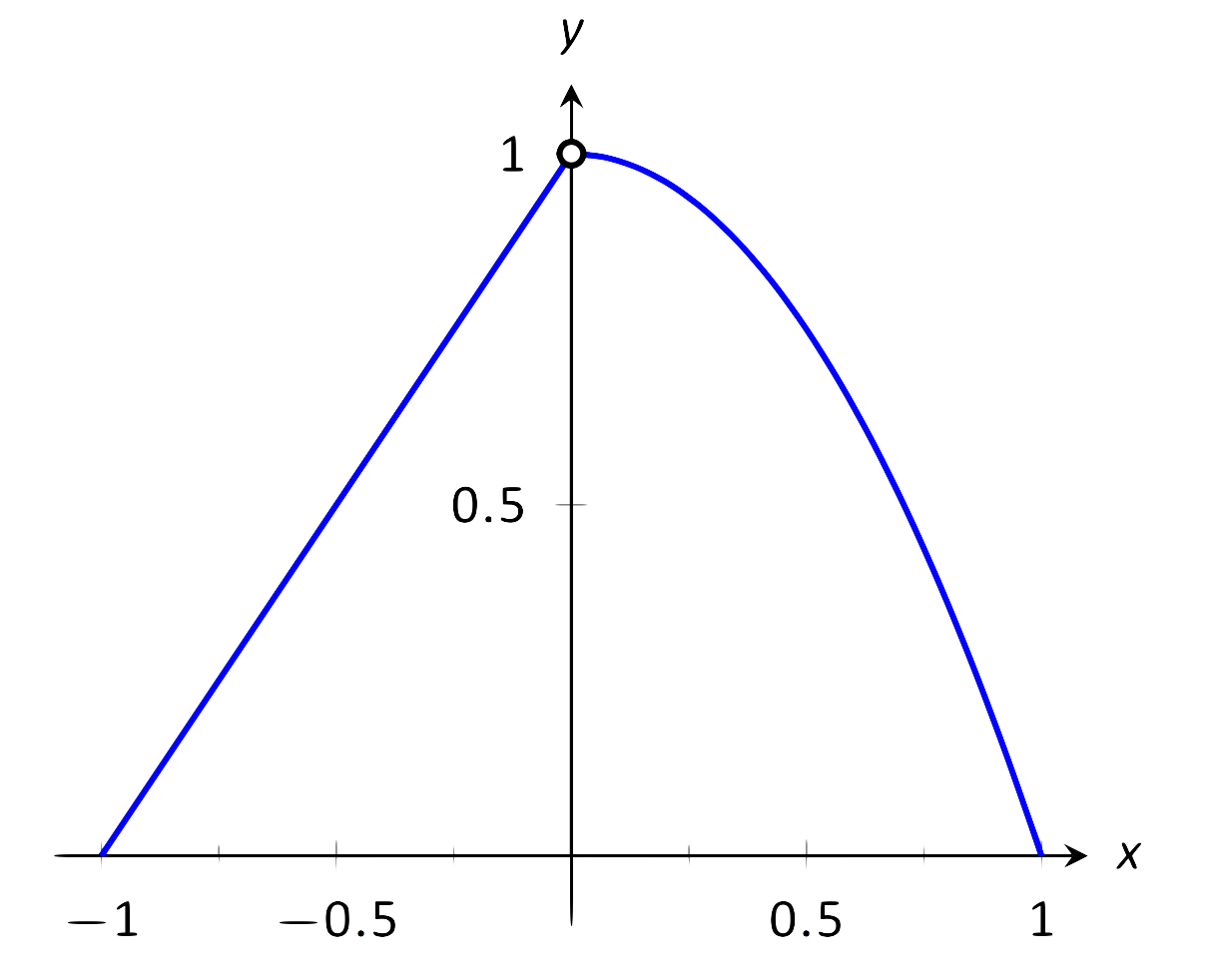
\(\text{FIGURE 1.7}\): Aproximando gráficamente un límite en el Ejemplo 2.
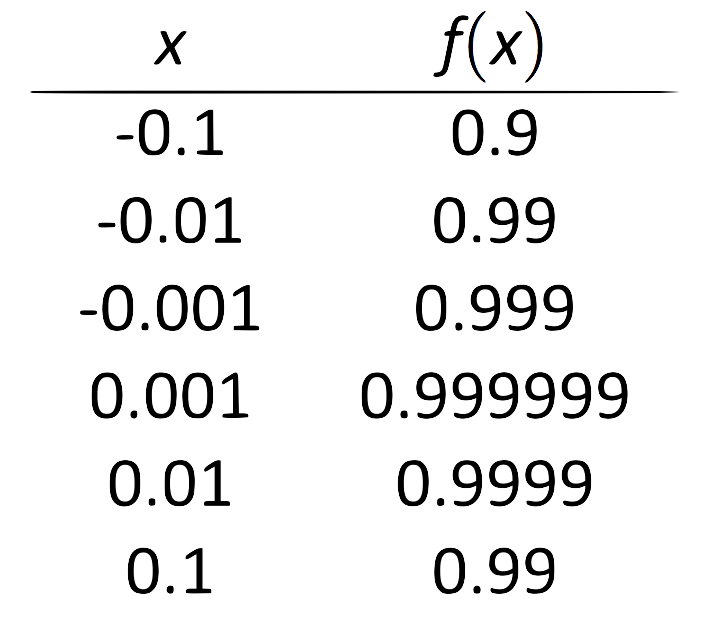
\(\text{FIGURE 1.8}\): Aproximando numéricamente un límite en el Ejemplo 2.
El cuadro que se muestra en la Figura 1.8 muestra valores de\(f(x)\) para valores\(x\) cercanos a 0. Es claro que como\(x\) toma valores muy cercanos a 0,\(f(x)\) toma valores muy cercanos a 1. Resulta que si dejamos\(x=0\) para alguna “pieza” de\(f(x)\), se devuelve 1; esto es significativo y volveremos a esta idea más adelante.
La gráfica y la tabla nos permiten decir eso\(\lim_{x\to 0}f(x) \approx 1\); de hecho, probablemente estamos muy seguros de que equivale a 1.
Identificar cuándo no existen límites
Una función puede no tener un límite para todos los valores de\(x\). Es decir, no podemos decir\(\lim_{x\to c}f(x)=L\) para algunos números\(L\) para todos los valores de\(c\), pues puede que no haya un número que\(f(x)\) se acerque. Hay tres formas en las que un límite puede no existir.
- La función\(f(x)\) puede acercarse a diferentes valores a cada lado de\(c\).
- La función puede crecer sin límite superior o inferior a medida que se\(x\) aproxima\(c\).
- La función puede oscilar a medida que se\(x\) aproxima\(c\).
Exploraremos cada uno de estos a su vez.
Ejemplo 3: Diferentes valores aproximados desde la izquierda y la derecha
Explora por qué\(\lim_{x\to 1} f(x)\) no existe, dónde
\[f(x) = \left\{\begin{array}{cl} x^2-2x+3 & x\leq 1 \\ x & x>1 \end{array}\right. \]
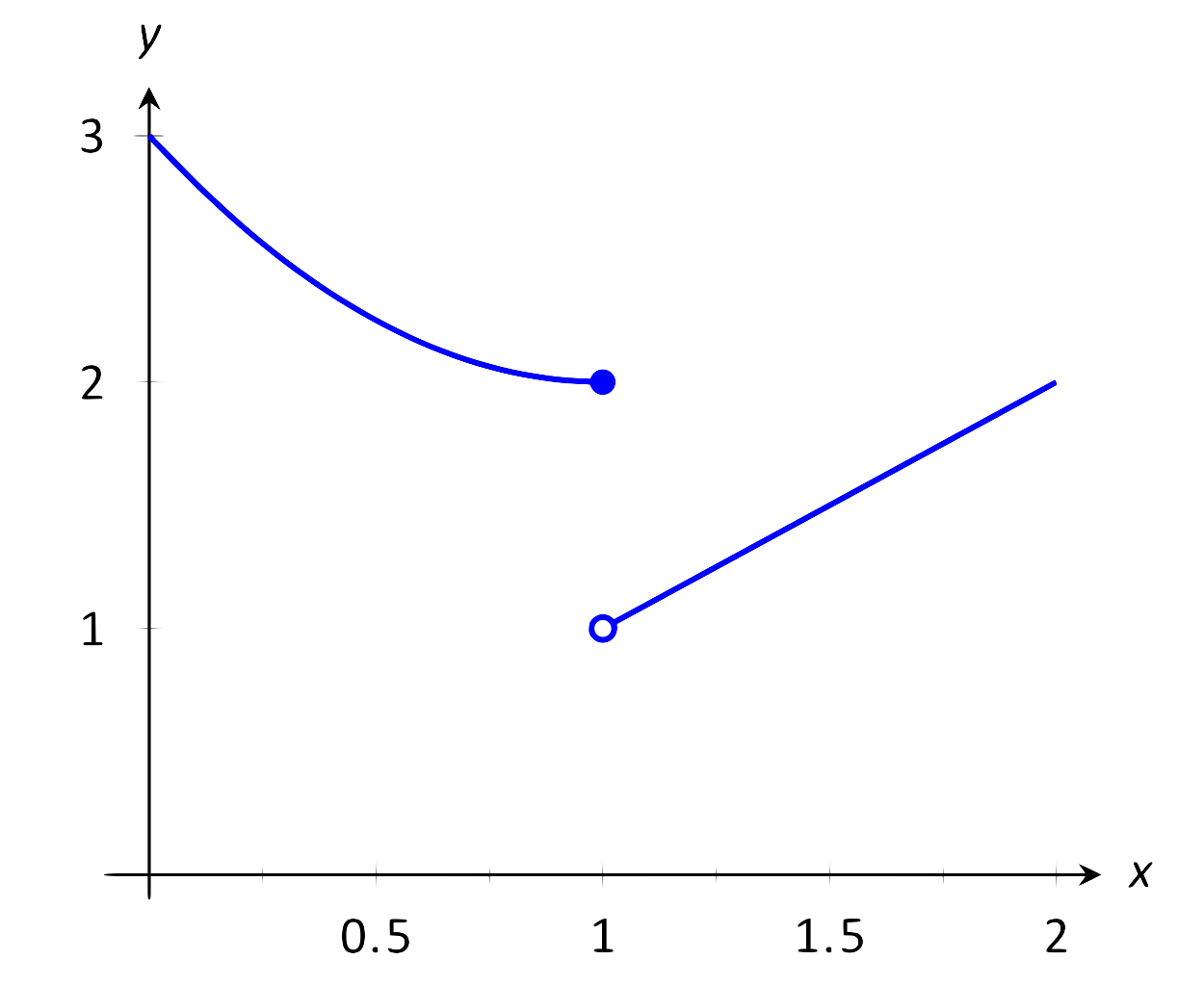
\(\text{FIGURE 1.9}\): No observar límite como\(x \to 1\) en el Ejemplo 3.

\(\text{FIGURE 1.10}\): Valores de\(f(x)\) cerca\(x=1\) en el Ejemplo 3.
Solución:
Una gráfica de\(f(x)\) alrededor\(x=1\) y una tabla se dan las Figuras 1.9 y 1.10, respectivamente. Es claro que a medida que\(x\) se acerca al 1,\(f(x)\) no parece acercarse a un solo número. En cambio, parece que se\(f(x)\) aproxima a dos números diferentes. Al considerar valores de\(x\) menos de 1 (acercándose a 1 desde la izquierda), parece que\(f(x)\) se acerca a 2; al considerar valores\(x\) mayores a 1 (acercándose a 1 desde la derecha), parece que\(f(x)\) se acerca a 1. Reconocer este comportamiento es importante; posteriormente lo estudiaremos con mayor profundidad. Ahora mismo, basta con decir que el límite no existe ya que no\(f(x)\) se acerca a un valor como se\(x\) acerca al 1.
Ejemplo 4: La función crece sin límite
Explora por qué\(\lim_{x\to 1} 1/(x-1)^2\) no existe.
Solución: En las Figuras 1.11 y 1.12\(f(x) = 1/(x-1)^2\) se dan
una gráfica y una tabla de, respectivamente. Ambos muestran que a medida que\(x\) se acerca 1,\(f(x)\) crece cada vez más grande.
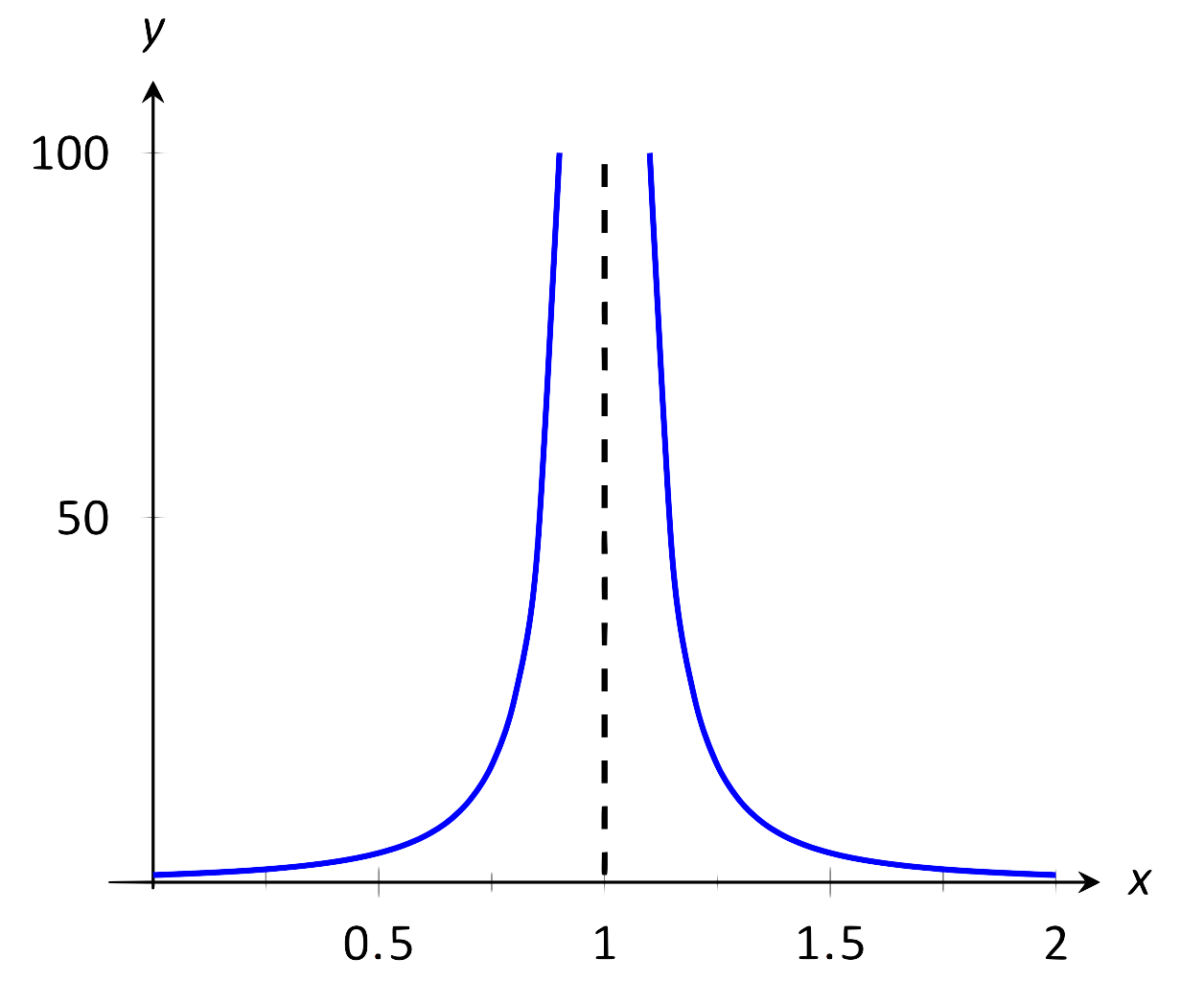
\(\text{FIGURE 1.11}\): No observar límite como\(x\to 1\) en el Ejemplo 4.
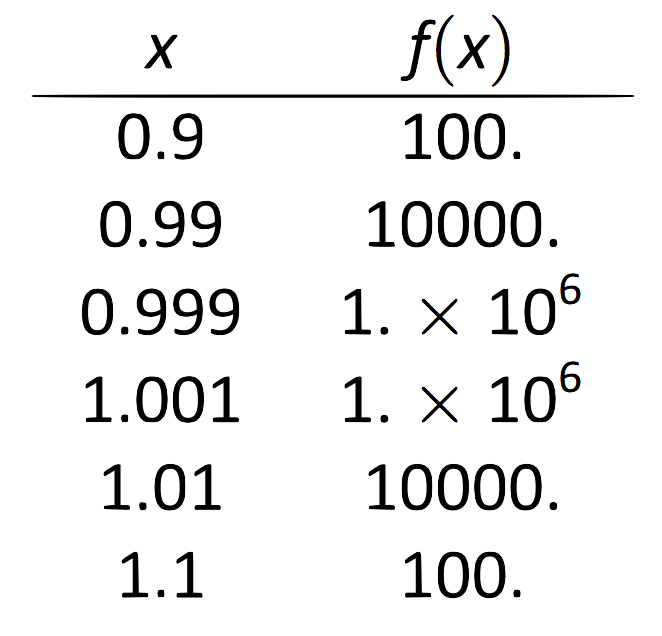
\(\text{FIGURE 1.12}\): Valores de\(f(x)\) cerca\(x=1\) en el Ejemplo 4.
Podemos deducir esto por nuestra cuenta, sin la ayuda de la gráfica y la tabla. Si\(x\) está cerca de 1, entonces\((x-1)^2\) es muy pequeño, y:
\[\frac{1}{\text{very small number}} = \text{very large number}.\]
Como no\(f(x)\) se acerca a un solo número, concluimos que
\[\lim_{x\to 1}\frac{1}{(x-1)^2}\]
no existe.
Ejemplo 5: La función oscila
Explora por qué\(\lim_{x\to 0}\sin(1/x)\) no existe.
Solución:
Dos gráficas de\(f(x) = \sin(1/x)\) se dan en las Figuras 1.13. La Figura 1.13 (a) muestra\(f(x)\) en el intervalo\([-1,1]\); observe cómo\(f(x)\) parece oscilar cerca\(x=0\). Se podría pensar que a pesar de la oscilación, a medida que se\(x\) acerca a 0,\(f(x)\) se acerca a 0. Sin embargo, la Figura 1.13 (b) amplía\(\sin(1/x)\), sobre el intervalo\([-0.1,0.1]\). Aquí la oscilación es aún más pronunciada. Finalmente, en la tabla de la Figura 1.13 (c), vemos\(\sin(x)/x\) evaluados para valores\(x\) cercanos a 0. A medida que\(x\) se acerca a 0,\(f(x)\) no parece acercarse a ningún valor.
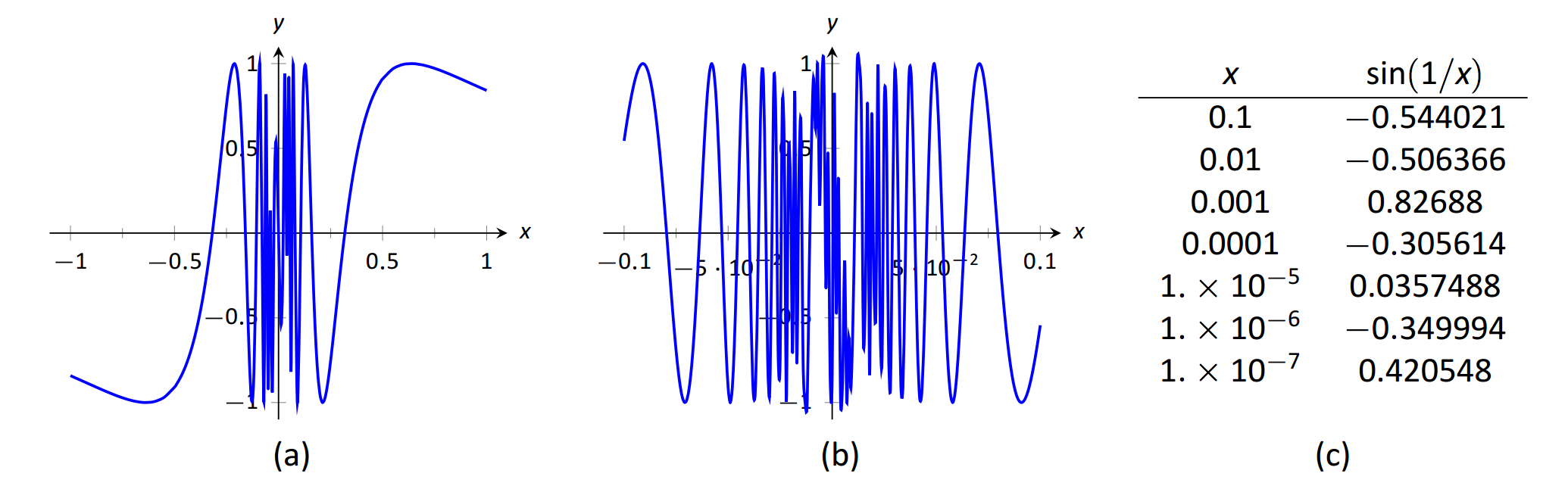
\(\text{FIGURE 1.13}\): Observando que no\(f(x)=\sin (1/x)\) tiene límite como\(x\to 0\) en el Ejemplo 5.
Se puede demostrar que en realidad, a medida que se\(x\) acerca a 0,\(\sin(1/x)\) adquiere todos los valores entre\(-1\) y ¡1 veces infinitas! Debido a esta oscilación,
\(\lim_{x\to 0}\sin(1/x)\)no existe.
Límites de Cocientes de Diferencia
Hemos aproximado los límites de las funciones a medida que\(x\) se aproximan a un número determinado. Consideraremos otro tipo importante de límite después de explicar algunas ideas clave.
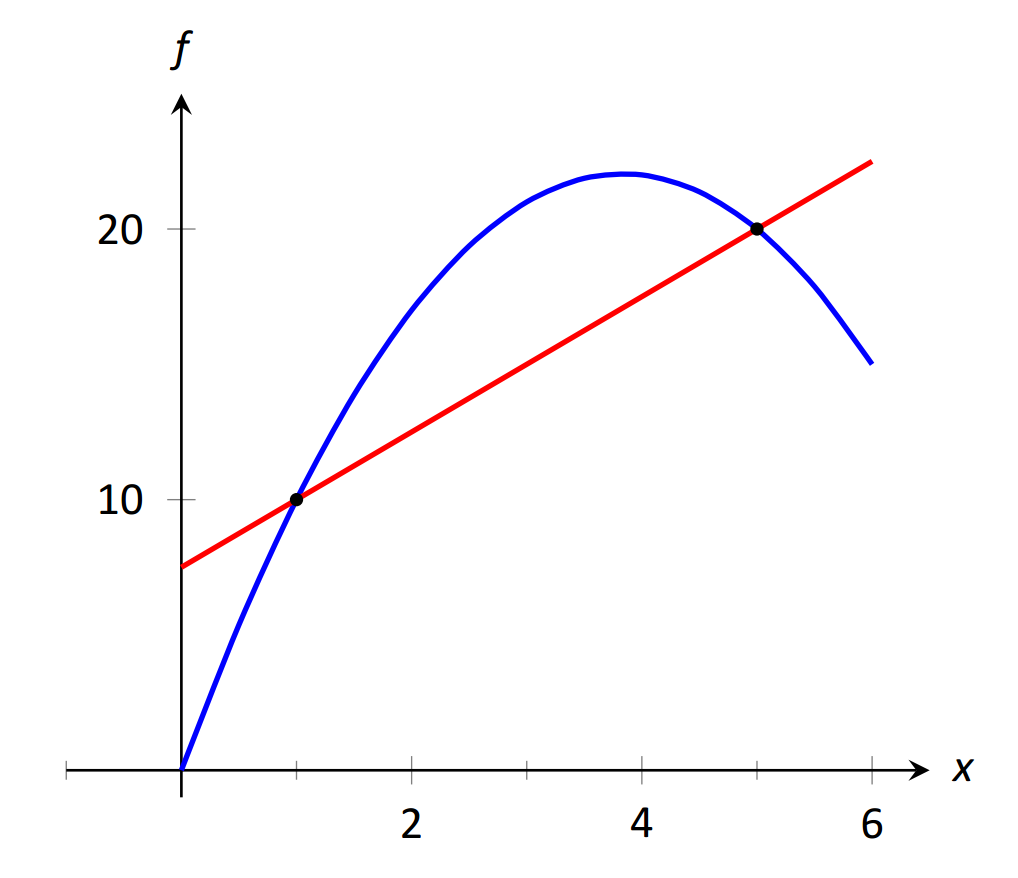
\(\text{FIGURE 1.14}\): Interpretar un cociente diferencial como la pendiente de una línea secante.
Dejar\(f(x)\) representar la función de posición, en pies, de alguna partícula que se mueve en línea recta, donde\(x\) se mide en segundos. Digamos que cuando\(x=1\), la partícula está en la posición 10 pies, y cuando\(x=5\), la partícula está a 20 pies. Otra forma de expresar esto es decir
\[f(1)=10 \quad \text{ and } \quad f(5) = 20.\]
Dado que la partícula viajó 10 pies en 4 segundos, podemos decir que la velocidad promedio de la partícula fue de 2.5 pies/s. Escribimos este cálculo usando un “cociente de diferencias” o, un cociente de diferencia:
\[\frac{f(5) - f(1)}{5-1} = \frac{10}4 = 2.5 \text{ft/s}.\]
Este cociente de diferencia se puede considerar como el familiar “ascenso sobre carrera” que se utiliza para calcular las pendientes de las líneas. De hecho, eso es esencialmente lo que estamos haciendo: dados dos puntos en la gráfica de\(f\), estamos encontrando la pendiente de la línea secante a través de esos dos puntos. Ver Figura 1.14.
Ahora considere encontrar la velocidad promedio en otro intervalo de tiempo. De nuevo empezamos en\(x=1\), pero consideramos la posición de la partícula\(h\) segundos después. Es decir, considere las posiciones de la partícula cuándo\(x=1\) y cuándo\(x=1+h\). El cociente de diferencia es ahora
\[\frac{f(1+h)-f(1)}{(1+h)-1} = \frac{f(1+h)-f(1)}h.\]
Que\(f(x) = -1.5x^2+11.5x\); anote eso\(f(1)=10\) y\(f(5) = 20\), como en nuestra discusión. Podemos calcular este cociente de diferencia para todos los valores de\(h\) (¡incluso valores negativos!) excepto\(h=0\), para entonces obtenemos “0/0”, la forma indeterminada introducida anteriormente. Para todos los valores\(h\neq 0\), el cociente de diferencia calcula la velocidad promedio de la partícula a lo largo de un intervalo de tiempo de longitud a\(h\) partir de\(x=1\).
Para valores pequeños de\(h\), es decir, valores\(h\) cercanos a 0, obtenemos velocidades promedio en periodos de tiempo muy cortos y calculamos líneas secantes a intervalos pequeños. Ver Figura 1.15. Esto nos lleva a preguntarnos cuál es el límite del cociente de diferencia a medida que se\(h\) acerca a 0. Es decir,
\[\lim_{h\to 0} \frac{f(1+h)-f(1)}{h} = \text{ ? }\]
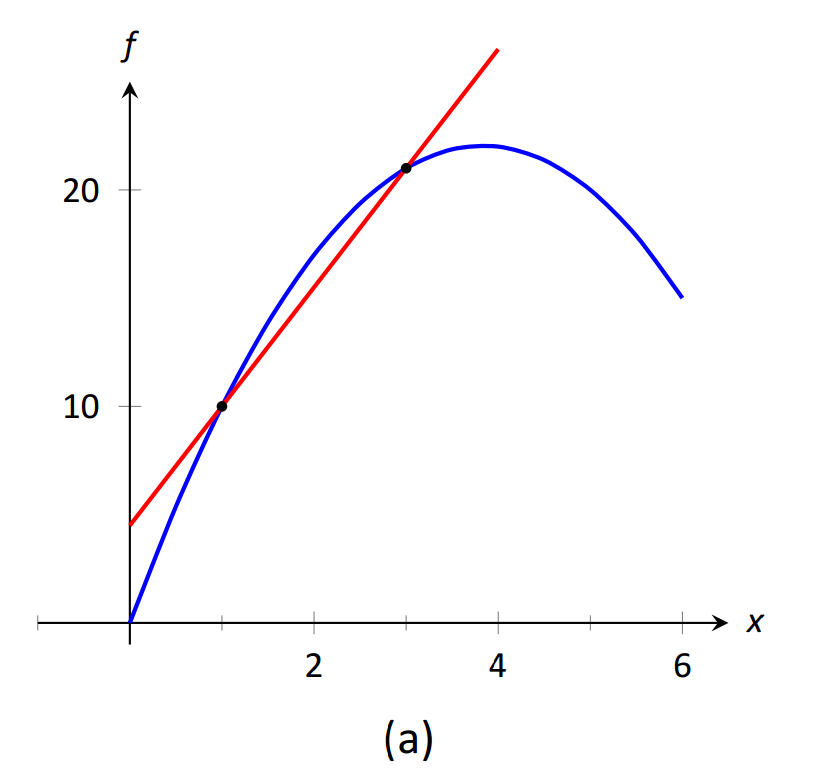
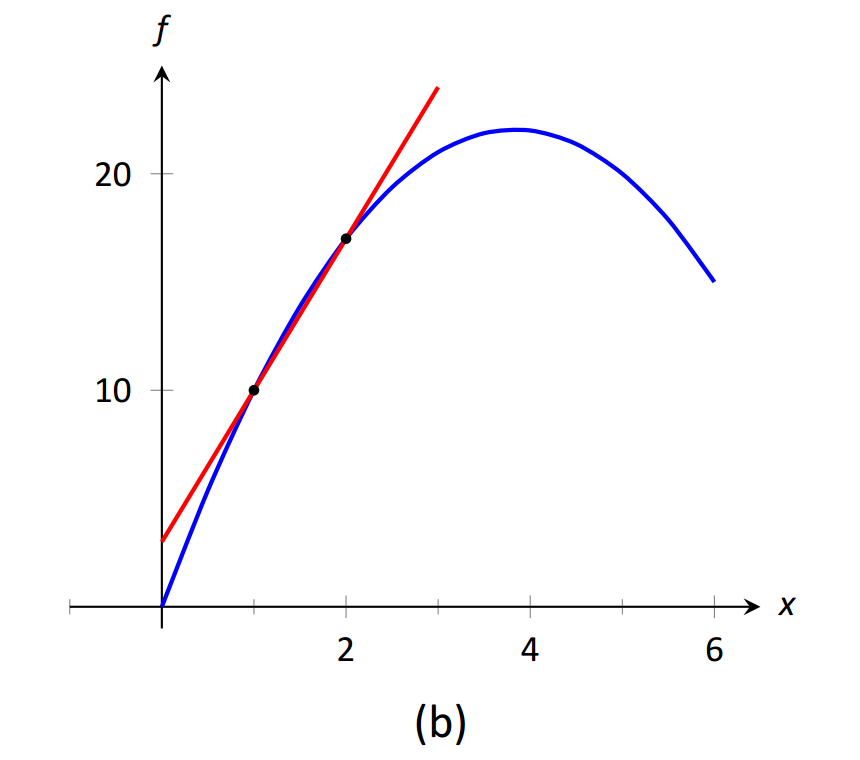
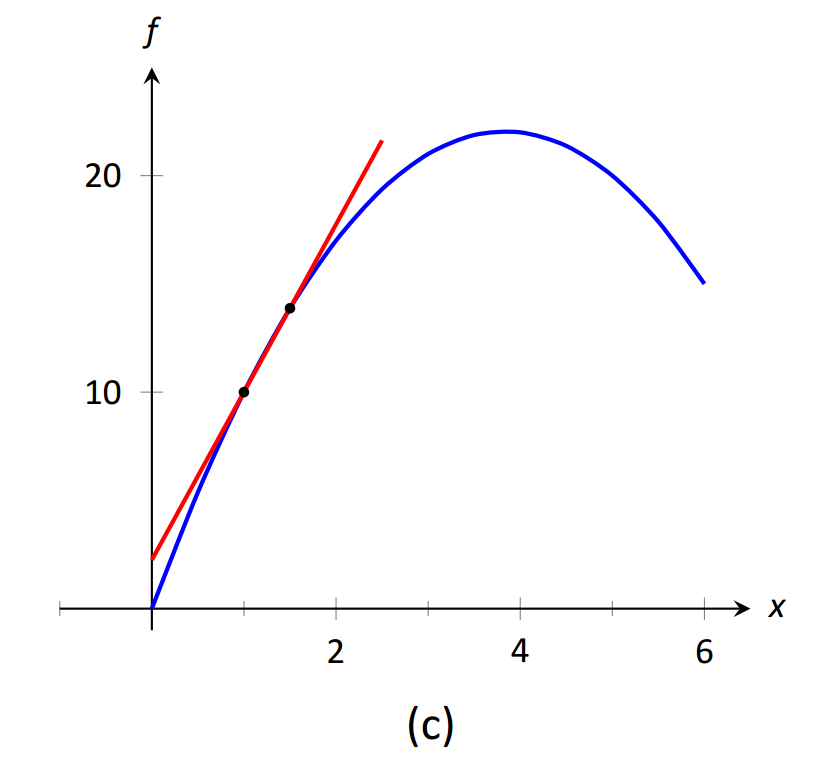
\(\text{FIGURE 1.15}\): Líneas secantes de\(f(x)\) at\(x=1\) y\(x=1+h\), para reducir los valores de\(h\) (es decir,\(h\to 0\)).
Como aún no tenemos una verdadera definición de límite ni un método exacto para calcularlo, nos conformamos con aproximar el valor. Si bien podríamos graficar el cociente de diferencia (donde el\(x\) eje -representaría\(h\) valores y el\(y\) eje representaría valores del cociente de diferencia) nos conformamos con hacer una tabla. Ver Figura 1.16. El cuadro nos da razones para asumir que el valor del límite es de aproximadamente 8.5.

\(\text{FIGURE 1.16}\): El cociente de diferencia evaluado a valores\(h\) cercanos a 0.
La comprensión adecuada de los límites es clave para comprender el cálculo. Con límites, podemos lograr cosas matemáticas aparentemente imposibles, como sumar un número infinito de números (y no obtener infinito) y encontrar la pendiente de una línea entre dos puntos, donde los “dos puntos” son en realidad el mismo punto. Estas no son solo curiosidades matemáticas; nos permiten vincular posición, velocidad y aceleración juntas, conectar áreas transversales al volumen, encontrar el trabajo realizado por una fuerza variable, y mucho más.
En la siguiente sección damos la definición formal del límite y comenzamos nuestro estudio de encontrar límites analíticamente. En los siguientes ejercicios, continuamos nuestra introducción y aproximamos el valor de los límites.


