1.3: Encontrar Límites Analíticamente

En la Sección 1.1 exploramos el concepto del límite sin una definición estricta, es decir, solo podríamos hacer aproximaciones. En el apartado anterior dimos la definición del límite y demostramos cómo usarlo para verificar que nuestras aproximaciones fueran correctas. Hasta ahora, nuestro método para encontrar un límite es 1) hacer una aproximación realmente buena ya sea gráfica o numéricamente, y 2) verificar que nuestra aproximación sea correcta usando una\(\delta\) prueba\(\epsilon\) -.

Este proceso tiene sus carencias, entre las cuales no menos importante es el hecho de que\(\epsilon\) — las\(\delta\) pruebas son engorrosas. Esta sección da una serie de teoremas que nos permiten encontrar límites de manera mucho más rápida e intuitiva.

Reconociendo que\(\epsilon\) - las\(\delta\) pruebas son engorrosas, esta sección da una serie de teoremas que permiten encontrar límites de manera mucho más rápida e intuitiva.

Supongamos que\(\lim\limits_{x\to 2} f(x)=2\) y\(\lim\limits_{x\to 2} g(x) = 3\). ¿Qué es\(\lim\limits_{x\to 2}(f(x)+g(x))\)? La intuición nos dice que el límite debe ser 5, ya que esperamos que los límites se comporten de una manera agradable. El siguiente teorema afirma que los límites ya establecidos sí se comportan bien.

Teorema\(\PageIndex{1}\): Basic Limit Properties

Let\(b\)\(c\),,\(L\) y\(K\) ser números reales, let\(n\) ser un entero positivo, y let\(f\) y\(g\) be funciones con los siguientes límites:

\[\lim\limits_{x\to c}f(x) = L \text{ and } \lim\limits_{x\to c} g(x) = K.\nonumber\]

Se mantienen los siguientes límites.

1. Constantes:\(\displaystyle \lim\limits_{x\to c} b = b\)
2. Identidad:\(\displaystyle \lim\limits_{x\to c} x = c\)
3. Sumas/Diferencias:\(\displaystyle \lim\limits_{x\to c}(f(x)\pm g(x)) = L\pm K\)
4. Multiplos escalares:\(\displaystyle \lim\limits_{x\to c} b\cdot f(x) = bL\)
5. Productos:\(\displaystyle \lim\limits_{x\to c} f(x)\cdot g(x) = LK\)
6. Cocientes:\(\displaystyle \lim\limits_{x\to c} f(x)/g(x) = L/K\), (\(K\neq 0)\)
7. Poderes:\(\displaystyle \lim\limits_{x\to c} f(x)^n = L^n\)
8. Raíces:\(\displaystyle \lim\limits_{x\to c} \sqrt[n]{f(x)} = \sqrt[n]{L}\)
9. Composiciones: Ajustar nuestra situación límite previamente dada a:

\[\lim\limits_{x\to c}f(x) = L,\ \lim\limits_{x\to L} g(x) = K \text{ and } g(L)=K .\]\[\text{Then } \lim\limits_{x\to c}g(f(x)) = K.\]

Hacemos una nota sobre la Propiedad #8: cuando\(n\) es par,\(L\) debe ser mayor a 0. Si\(n\) es impar, entonces la declaración es verdadera para todos\(L\).

Aplicamos el teorema a un ejemplo.

Ejemplo\(\PageIndex{1}\): Using Basic Limit Properties

Vamos

\[\lim\limits_{x\to 2} f(x)=2,\quad\lim\limits_{x\to 2} g(x) = 3\quad \text{ and }\quad p(x) = 3x^2-5x+7.\]

Encuentra los siguientes límites:

1. \( \lim\limits_{x\to 2} \big(f(x) + g(x)\big)\)
2. \( \lim\limits_{x\to 2} \big(5f(x) + g(x)^2\big)\)
3. \( \lim\limits_{x\to 2} p(x)\)

Solución

1. Usando la regla Suma/Diferencia, lo sabemos\( \lim\limits_{x\to 2} \big(f(x) + g(x)\big) = 2+3 =5\).
2. Usando las reglas Scalar Multiple y Sum/Difference, encontramos que\( \lim\limits_{x\to 2} \big(5f(x) + g(x)^2\big) = 5\cdot 2 + 3^2 = 19.\)
3. Aquí combinamos las Reglas de Poder, Múltiple Escalar, Suma/Diferencia y Constante. Mostramos bastantes pasos, pero en general estos se pueden omitir:

\[\begin{align*} \lim\limits_{x\to 2} p(x) &= \lim\limits_{x\to 2} (3x^2-5x+7) \\ &= \lim\limits_{x\to 2} 3x^2-\lim\limits_{x\to 2} 5x+\lim\limits_{x\to 2}7 \\ &= 3\cdot 2^2 - 5\cdot 2+7 \\ &= 9 \end{align*}\]

La parte 3 del ejemplo anterior demuestra cómo se puede determinar el límite de un polinomio cuadrático usando las propiedades del Teorema 1. No solo eso, reconozca que

\[\lim\limits_{x\to 2} p(x) = 9 = p(2);\]

es decir, el límite en 2 se encontró simplemente enchufando 2 a la función. Esto es válido para todos los polinomios, y también para las funciones racionales (que son cocientes de polinomios), como se afirma en el siguiente teorema.

Teorema\(\PageIndex{2}\) : Limits of Polynomial and Rational Functions

Límites de Funciones Polinómicas y Racionales} {Dejar\(p(x)\) y\(q(x)\) ser polinomios y\(c\) un número real. Entonces:

1. \( \lim\limits_{x\to c} p(x) = p(c)\)
2. \( \lim\limits_{x\to c} \frac{p(x)}{q(x)} = \frac{p(c)}{q(c)}\), donde\(q(c) \neq 0\).

Ejemplo\(\PageIndex{2}\): Finding a limit of a rational function

Usando el Teorema 2, encontrar

\[\lim\limits_{x\to -1} \frac{3x^2-5x+1}{x^4-x^2+3}. \nonumber\]

Solución

Usando el teorema\(\PageIndex{2}\), podemos afirmar rápidamente que

\[\begin{align*} \lim\limits_{x\to -1}\frac{3x^2-5x+1}{x^4-x^2+3} &= \frac{3(-1)^2-5(-1)+1}{(-1)^4-(-1)^2+3} \\ &= \frac{9}{3} =3. \end{align*}\]

Probablemente fue frustrante en la Sección 1.2 hacer mucho trabajo para demostrar que

\[\lim\limits_{x\to 2} x^2 = 4\]

ya que parecía bastante obvio. Los teoremas anteriores afirman que muchas funciones se comportan de una manera tan “obvia”, como lo demuestra la función racional en el Ejemplo 11.

Las funciones polinomiales y racionales no son las únicas funciones que se comportan de una manera tan predecible. El siguiente teorema da una lista de funciones cuyo comportamiento es particularmente “agradable” en términos de límites. En la siguiente sección, daremos un nombre formal a estas funciones que se comportan “muy bien”.

Teorema\(\PageIndex{4}\): Special Limits

Dejar\(c\) ser un número real en el dominio de la función dada y dejar\(n\) ser un entero positivo. Se mantienen los siguientes límites:

\[\begin{align} &1.\lim\limits_{x\to c} \sin x = \sin c \quad &&4. \lim\limits_{x\to c} \csc x = \csc c\quad &&&7.\lim\limits_{x\to c} a^x = a^c (a>0) \\ &2. \lim\limits_{x\to c} \cos x = \cos c \quad &&5. \lim\limits_{x\to c} \sec x = \sec c \quad &&&8.\lim\limits_{x\to c} \ln x = \ln c \\ &3. \lim\limits_{x\to c} \tan x = \tan c \quad &&6.\lim\limits_{x\to c} \cot x = \cot c \quad &&&9. \lim\limits_{x\to c} \sqrt[n]{x} = \sqrt[n]{c} \end{align}\]

Ejemplo\(\PageIndex{3}\): Evaluating limits analytically

Evaluar los siguientes límites.

1. \(\lim\limits_{x\to \pi} \cos x\)
2. \( \lim\limits_{x\to 3} (\sec^2x - \tan^2 x)\)
3. \( \lim\limits_{x\to \pi/2} \cos x\sin x\)
4. \( \lim\limits_{x\to 1} e^{\ln x}\)
5. \( \lim\limits_{x\to 0} \frac{\sin x}{x}\)

Solución

1. Esta es una aplicación sencilla del Teorema 3. \(\lim\limits_{x\to \pi} \cos x = \cos \pi = -1\).
2. Podemos abordar esto por lo menos de dos maneras. Primero, aplicando directamente el Teorema 3, tenemos:\[\lim\limits_{x\to 3} (\sec^2x - \tan^2 x) = \sec^23-\tan^23.\] Usando el Teorema de Pitágoras, esta última expresión es 1; por lo tanto también\[\lim\limits_{x\to 3} (\sec^2x - \tan^2 x) = 1.\] podemos usar el Teorema de Pitágoras desde el inicio. \[\lim\limits_{x\to 3} (\sec^2x - \tan^2 x) = \lim\limits_{x\to 3} 1 = 1,\]usando la regla de Límite constante. De cualquier manera, encontramos que el límite es 1.
3. Aplicando la regla de Límite de Producto del Teorema 1 y Teorema 3 da\[ \lim\limits_{x\to \pi/2} \cos x\sin x = \cos (\pi/2)\sin(\pi/2) = 0\cdot 1 = 0.\]
4. Nuevamente, podemos abordar esto de dos maneras. En primer lugar, podemos utilizar la identidad exponencial/logarítmica que\(e^{\ln x} = x\) y evaluar También\( \lim\limits_{x\to 1} e^{\ln x} = \lim\limits_{x\to 1} x = 1.\)
   podemos utilizar el límite Composición Regla del Teorema 1. Utilizando el Teorema 3, tenemos\( \lim\limits_{x\to 1}\ln x = \ln 1 = 0\) y\(\lim\limits_{x\to 0} e^x= e^0=1\), satisfaciendo las condiciones de la Regla de Composición. Aplicando esta regla,\[ \lim\limits_{x\to 1} e^{\ln x} = \lim\limits_{x\to 0} e^x = e^0 = 1.\] Ambos enfoques son válidos, dando el mismo resultado.
5. Encontramos este límite en la Sección 1.1. Aplicando nuestros teoremas, intentamos encontrar el límite como\[\lim\limits_{x\to 0}\frac{\sin x}{x}\rightarrow \frac{\sin 0}{0} \rightarrow \frac{"\,0\,"}{0}.\] Esto, por supuesto, viola una condición del Teorema 1, ya que no se permite que el límite del denominador sea 0. Por lo tanto, seguimos siendo incapaces de evaluar este límite con herramientas que actualmente tenemos a mano.

La sección podría haber sido titulada “Uso de límites conocidos para encontrar límites desconocidos”. Al conocer ciertos límites de funciones, podemos encontrar límites que involucran sumas, productos, poderes, etc., de estas funciones. Proseguimos el desarrollo de este tipo de herramientas comparativas con el Teorema de Squeeze, una forma inteligente e intuitiva de encontrar el valor de algunos límites.

Antes de afirmar este teorema formalmente, supongamos que tenemos funciones\(f\),\(g\) y\(h\) donde\(g\) siempre toma valores entre\(f\) y\(h\); es decir, para todos\(x\) en un intervalo,

\[f(x) \leq g(x) \leq h(x).\]

Si\(f\) y\(h\) tienen el mismo límite en\(c\), y siempre\(g\) se “aprieta” entre ellos, entonces\(g\) debe tener el mismo límite también. Eso es lo que afirma el Teorema de Squeeze.

Teorema\(\PageIndex{5}\): Squeeze Theorem

Dejar\(f\),\(g\) y\(h\) ser funciones en un intervalo abierto\(I\) que contenga\(c\) tal que para todos\(x\) en\(I\),

\[f(x)\leq g(x) \leq h(x).\]

Si

\[\lim\limits_{x\to c} f(x) = L = \lim\limits_{x\to c} h(x),\]

entonces

\[\lim\limits_{x\to c} g(x) = L.\]

Puede tomar algún trabajo para averiguar las funciones adecuadas mediante las cuales “exprimir” la función dada de la cual está tratando de evaluar un límite. No obstante, ese es generalmente el único lugar donde el trabajo es necesario; el teorema hace muy simple la “evaluación de la parte límite”.

Usamos el Teorema de Squeeze en el siguiente ejemplo para finalmente probarlo\( \lim\limits_{x\to 0} \frac{\sin x}{x} = 1\).

Ejemplo\(\PageIndex{4}\): Using the Squeeze Theorem

Usa el Teorema de Squeeze para demostrar que

\[ \lim\limits_{x\to 0} \frac{\sin x}{x} = 1. \nonumber\]

Solución

Comenzamos por considerar el círculo unitario. Cada punto en el círculo unitario tiene coordenadas\((\cos \theta,\sin \theta)\) para algún ángulo\(\theta\) como se muestra en la Figura\(\PageIndex{1}\). Usando triángulos similares, podemos extender la línea desde el origen a través del punto hasta el punto\((1,\tan \theta)\), como se muestra. (Aquí estamos suponiendo que\(0\leq \theta \leq \pi/2\) .Posteriormente vamos a demostrar que también podemos considerar\(\theta \leq 0\).)

Figura\(\PageIndex{1}\): El círculo unitario y los triángulos relacionados.

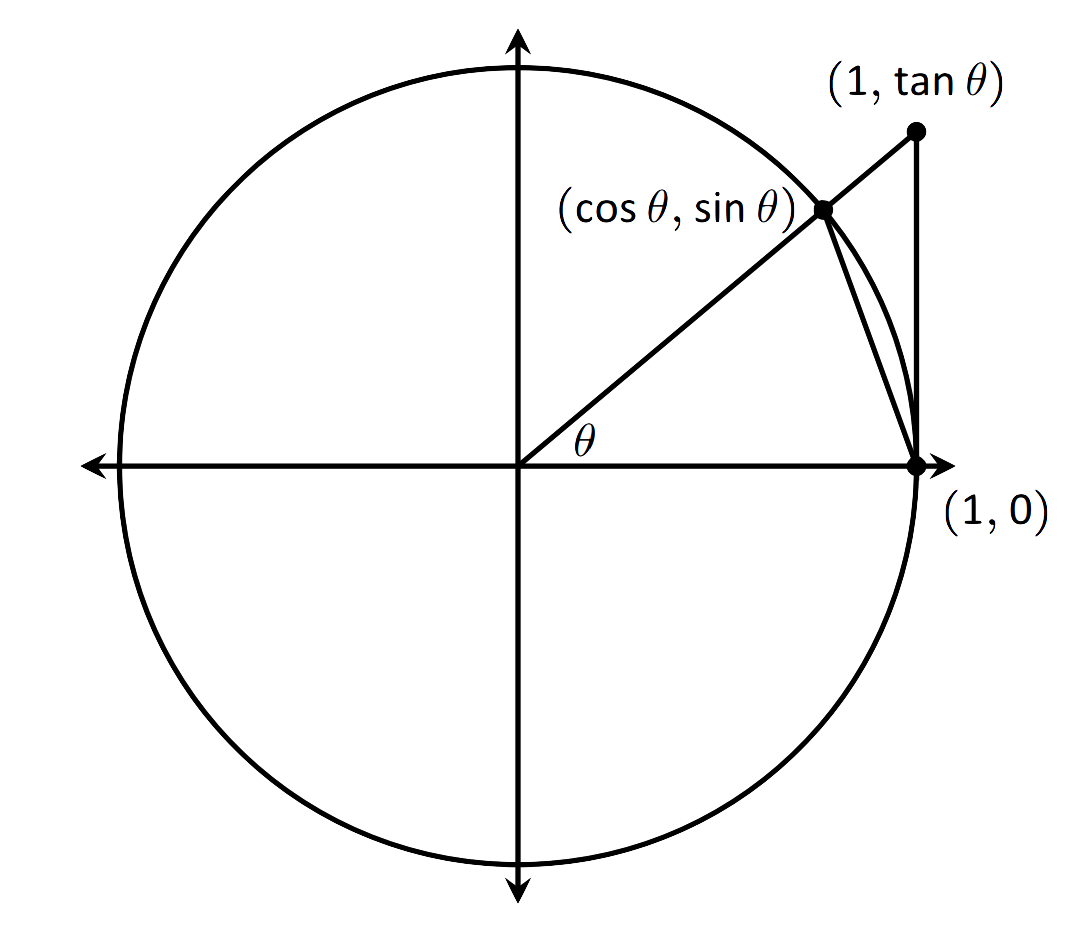
En la figura 1.19 se muestran tres regiones que se han construido en el primer cuadrante, dos triángulos y un sector de círculo, que también se dibujan a continuación. El área del triángulo grande es\(\frac12\tan\theta\); el área del sector es\(\theta/2\); el área del triángulo contenido dentro del sector es\(\frac12\sin\theta\). Entonces queda claro del diagrama que

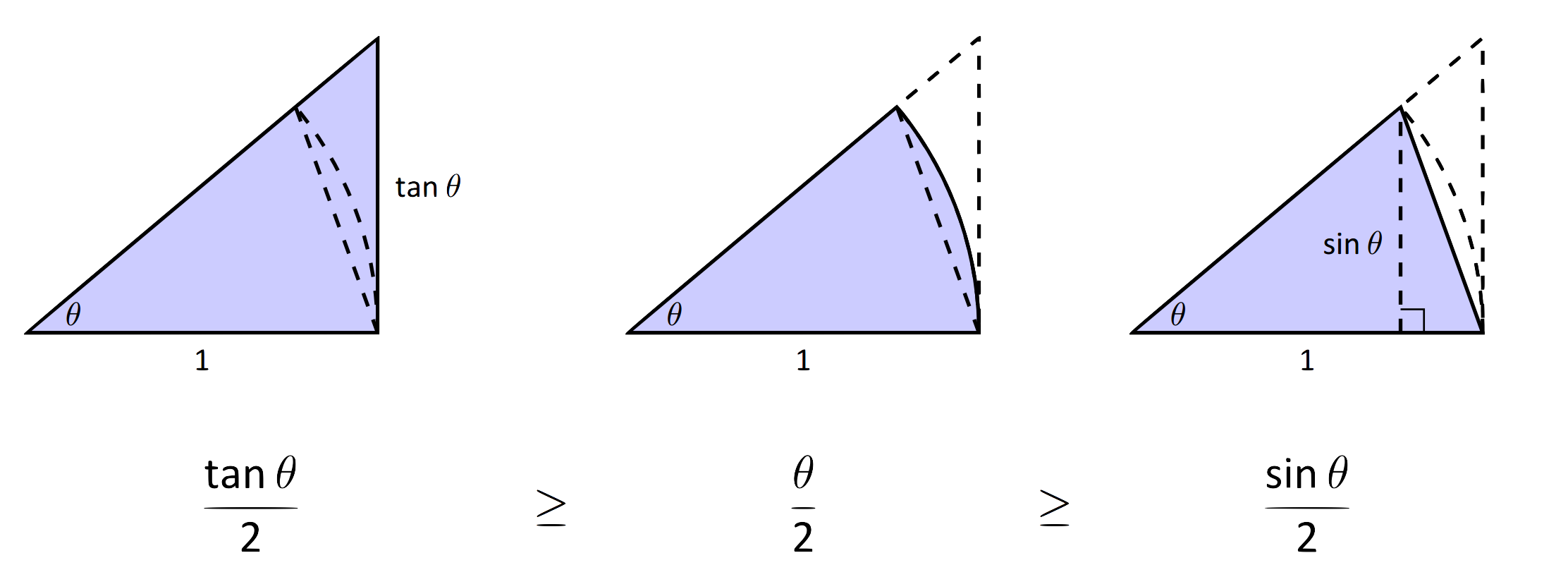
Multiplicar todos los términos por\(\frac{2}{\sin \theta}\), dando

\[\frac{1}{\cos\theta} \geq \frac{\theta}{\sin \theta} \geq 1.\]

Tomar reciprocas revierte las desigualdades, dar

\[ \cos \theta \leq \frac{\sin \theta}{\theta} \leq 1.\]

(Estas desigualdades se mantienen para todos los valores de\(\theta\) cerca de 0, incluso valores negativos, ya\(\cos (-\theta) = \cos \theta\) y\(\sin (-\theta) = -\sin \theta\).)

Ahora toma límites.

\[\lim\limits_{\theta\to 0} \cos \theta \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq \lim\limits_{\theta\to 0} 1 \]

\[\cos 0 \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq 1 \]

\[1 \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq 1 \]

Claramente esto significa que\( \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta}=1\)

Vale la pena mencionar dos notas sobre el ejemplo anterior. Primero, uno podría desanimarse con esta aplicación, pensando “Nunca se me hubiera ocurrido eso por mi cuenta. ¡Esto es demasiado duro!” No te desanimes; dentro de este texto te guiaremos en tu uso del Teorema de Squeeze. A medida que uno gana madurez matemática, pruebas inteligentes como esta son cada vez más fáciles de crear.

Segundo, este límite nos dice más que solo eso a medida que se\(x\) acerca a 0,\(\sin(x)/x\) se acerca al 1. Ambos\(x\) y\(\sin x\) se acercan a 0, pero la proporción de\(x\) y\(\sin x\) se acerca a 1, lo que significa que se acercan a 0 esencialmente de la misma manera. Otra forma de ver esto es: para pequeños\(x\), las funciones\(y=x\) y\(y=\sin x\) son esencialmente indistinguibles.

Incluimos este límite especial, junto con otros tres, en el siguiente teorema.

Teorema\(\PageIndex{5}\) : Special Limits

1. \( \lim\limits_{x\to 0} \frac{\sin x}{x} = 1\)
2. \( \lim\limits_{x\to 0} \frac{\cos x-1}{x} = 0\)
3. \( \lim\limits_{x\to 0} (1+x)^\frac1x = e\)
4. \( \lim\limits_{x\to 0} \frac{e^x-1}{x} = 1\)

Una breve palabra sobre cómo interpretar estos tres últimos límites. Sabemos que como\(x\) va a 0,\(\cos x\) va a 1. Entonces, en el segundo límite, tanto el numerador como el denominador se acercan a 0. No obstante, dado que el límite es 0, podemos interpretar esto como decir que "\(\cos x\)se acerca a 1 más rápido que\(x\) se acerca a 0”.

En el tercer límite, dentro de los paréntesis tenemos una expresión que se acerca a 1 (aunque nunca equivale a 1), y sabemos que 1 elevado a cualquier potencia sigue siendo 1. Al mismo tiempo, el poder crece hacia el infinito. ¿Qué sucede con un número cercano al 1 elevado a una potencia muy grande? En este caso particular, el resultado se aproxima al número de Euler\(e\), aproximadamente\(2.718.\)

En el cuarto límite, vemos que as\(x\to 0\),\(e^x\) se acerca a 1 ``tan rápido” como\(x\to 0\), resultando en un límite de 1.

Nuestro teorema final para esta sección estará motivado por el siguiente ejemplo.

Ejemplo\(\PageIndex{5}\): Using algebra to evaluate a limit

Evalúe el siguiente límite:

\[\lim\limits_{x\to 1}\frac{x^2-1}{x-1}. \nonumber\]

Solución

Comenzamos intentando aplicar el Teorema 3 y sustituyendo 1 por\(x\) en el cociente. Esto da:

\[\lim\limits_{x\to 1}\frac{x^2-1}{x-1} = \frac{1^2-1}{1-1} = \frac{"\,0\,"}{0},\]

y forma indeterminada. No podemos aplicar el teorema.

Figura\(\PageIndex{2}\): Graficando\(f\) en Ejemplo\(\PageIndex{5}\) para entender un límite.

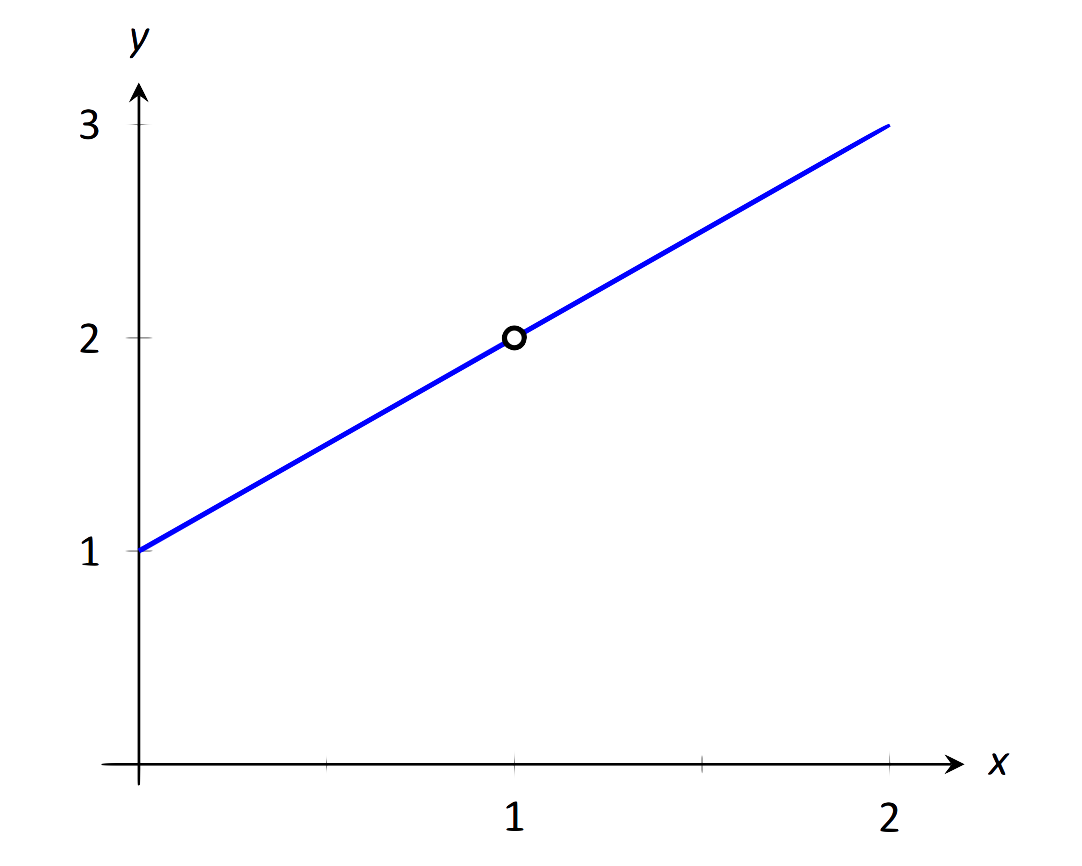
Al graficar la función, como en la Figura\(\PageIndex{2}\), vemos que la función parece ser lineal, lo que implica que el límite debe ser fácil de evaluar. Reconocer que el numerador de nuestro cociente puede ser factorizado:

\[\frac{x^2-1}{x-1} = \frac{(x-1)(x+1)}{x-1}. \nonumber\]

La función no se define cuando\(x=1\), sino para todos los demás\(x\),

\[\require{cancel} \frac{x^2-1}{x-1} = \frac{(x-1)(x+1)}{x-1} = \frac{\cancel{(x-1)}(x+1)}{\cancel{x-1}}= x+1.\]

Claramente\( \lim\limits_{x\to 1}x+1 = 2\). Recordemos que al considerar límites, no nos preocupa el valor de la función en 1, solo el valor que la función se acerca a la medida que se\(x\) acerca a 1. Dado que\((x^2-1)/(x-1)\) y\(x+1\) son iguales en todos los puntos excepto\(x=1\), ambos se acercan al mismo valor que\(x\) los enfoques 1. Por lo tanto podemos concluir que

\[\lim\limits_{x\to 1}\frac{x^2-1}{x-1}=2. \nonumber\]

La clave del ejemplo anterior es que las funciones\(y=(x^2-1)/(x-1)\) y\(y=x+1\) son idénticas excepto en\(x=1\). Dado que los límites describen un valor que se acerca la función, no el valor que realmente alcanza la función, los límites de las dos funciones son siempre iguales.

Teorema\(\PageIndex{6}\) : Limits of Functions Equal At All But One Point

Dejar\(g(x) = f(x)\) para todos\(x\) en un intervalo abierto, excepto posiblemente en\(c\), y dejar\( \lim\limits_{x\to c} g(x) = L\) para algún número\(L\) real.Entonces

\[\lim\limits_{x\to c}f(x) = L.\]

El Teorema Fundamental del Álgebra nos dice que cuando se trata de una función racional de la forma\(g(x)/f(x)\) y evaluar directamente el límite\( \lim\limits_{x\to c} \frac{g(x)}{f(x)}\) devuelve “0/0", entonces\((x-c)\) es un factor de ambos\(g(x)\) y\(f(x)\). Entonces se puede usar álgebra para factorizar este término, cancelar, luego aplicar el Teorema 6. Esto lo demostramos una vez más.

Ejemplo\(\PageIndex{6}\): Evaluating a limit using Theorem \(\PageIndex{6}\)

Evaluar

\[ \lim\limits_{x\to 3} \frac{x^3-2 x^2-5 x+6}{2 x^3+3 x^2-32 x+15}. \nonumber\]

Solución

Comenzamos aplicando el Teorema 3 y sustituyendo 3 por\(x\) .Esto devuelve la forma familiar indeterminada de “0/0".

Ya que el numerador y denominador son cada polinomios, sabemos que\((x-3)\) es factor de cada uno. Usar cualquier método que sea más cómodo para ti, factorizar\((x-3)\) de cada uno (usando división polinómica, división sintética, un sistema de álgebra computacional, etc.). Encontramos que

\[\frac{x^3-2 x^2-5 x+6}{2 x^3+3 x^2-32 x+15} = \frac{(x-3)(x^2+x-2)}{(x-3)(2 x^2+9 x-5)}. \nonumber\]

Podemos cancelar los\((x-3)\) términos siempre y cuando\(x\neq 3\). Usando el Teorema 6 concluimos:

\[\begin{align*}\lim\limits_{x\to 3} \frac{x^3-2 x^2-5 x+6}{2 x^3+3 x^2-32 x+15} &= \lim\limits_{x\to 3}\frac{(x-3)(x^2+x-2)}{(x-3)(2 x^2+9 x-5)} \\ &= \lim\limits_{x\to 3} \frac{(x^2+x-2)}{(2 x^2+9 x-5)}\\ &= \frac{10}{40} = \frac14. \end{align*}\]

Terminamos esta sección revisitando un límite visto por primera vez en la Sección 1.1, un límite de un cociente de diferencia. Vamos\(f(x) = -1.5x^2+11.5x\); aproximamos el límite\( \lim\limits_{h\to 0}\frac{f(1+h)-f(1)}{h}\approx 8.5.\) Evaluamos formalmente este límite en el siguiente ejemplo.

Ejemplo\(\PageIndex{7}\) : Evaluating the limit of a difference quotient

Let\(f(x) = -1.5x^2+11.5x\); encontrar\( \lim\limits_{h\to 0}\frac{f(1+h)-f(1)}{h}.\)

Solución

Dado que\(f\) es un polinomio, nuestro primer intento debe ser emplear el Teorema 3 y sustituir 0 por\(h\). No obstante, vemos que esto nos da “0/0”. Saber que tenemos una función racional insinúa que algún álgebra ayudará. Considera los siguientes pasos:

\[\begin{align*} \lim\limits_{h\to 0}\frac{f(1+h)-f(1)}{h} &= \lim\limits_{h\to 0}\frac{-1.5(1+h)^2 + 11.5(1+h) - \left(-1.5(1)^2+11.5(1)\right)}{h} \\ &= \lim\limits_{h\to 0}\frac{-1.5(1+2h+h^2) + 11.5+11.5h - 10}{h}\\ &= \lim\limits_{h\to 0}\frac{-1.5h^2 +8.5h}{h}\\ &= \lim\limits_{h\to 0}\frac{h(-1.5h+8.5)}h\\ &= \lim\limits_{h\to 0}(-1.5h+8.5) \quad (\text{using Theorem 6, as \(h\neq 0\)}) \\ &= 8.5 \quad (\text{using Theorem 3}) \end{align*}\]

Esto coincide con nuestra aproximación anterior.

Esta sección contiene varias herramientas valiosas para evaluar los límites. Uno de los principales resultados de esta sección es el Teorema 3; afirma que muchas funciones que utilizamos regularmente se comportan de una manera muy agradable, predecible. En la siguiente sección le damos un nombre a este comportamiento agradable; etiquetamos tales funciones como continuas. Definir ese término requerirá que volvamos a mirar qué es un límite y qué hace que los límites no existan.

Colaboradores y Atribuciones

• Template:ContribApexCalc