1.4: Límites de un solo lado

Última actualización
Guardar como PDF

Page ID: 111863

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Introducimos el concepto de límite suavemente, aproximando sus valores gráfica y numéricamente. Luego vino la rigurosa definición del límite, junto con un método ciertamente tedioso para evaluarlos. El apartado anterior nos dio herramientas (que llamamos teoremas) que nos permiten computar límites con mayor facilidad. Entre los resultados destacan los hechos de que polinomios y funciones racionales, trigonométricas, exponenciales y logarítmicas (y sus sumas, productos, etc.) se comportan “bien”. En esta sección definimos rigurosamente lo que queremos decir con “amablemente”.

En la Sección 1.1 exploramos las tres formas en que los límites de las funciones no existieron:

La función se aproximó a diferentes valores desde la izquierda y la derecha,
La función crece sin ataduras, y
La función oscila.

En esta sección exploramos en profundidad los conceptos detrás de #1 introduciendo el límite unilateral. Comenzamos con definiciones formales que son muy similares a la definición del límite dada en la Sección 1.2, pero la notación es ligeramente diferente y$x\neq c$ "" se sustituye por "$x<c$" o "”$x>c$.

Definición 2: Límites de un solo lado

Límite izquierdo

Dejar$I$ ser un intervalo abierto que contiene$c$, y dejar$f$ ser una función definida en$I$, excepto posiblemente en$c$. El límite de$f(x)$, cuando se$x$$c$ aproxima desde la izquierda, es$L$, o, el límite izquierdo—mano de$f$ at$c$ es$L$, denotado por

\[ \lim\limits_{x\rightarrow c^-} f(x) = L,\]

significa que dada alguna$\epsilon > 0$, existe$\delta > 0$ tal que para todos$x< c$, si$|x - c| < \delta$, entonces$|f(x) - L| < \epsilon$.

Límite derecho

Dejar$I$ ser un intervalo abierto que contiene$c$, y dejar$f$ ser una función definida en$I$, excepto posiblemente en$c$. El límite de$f(x)$, a medida que$x$ se$c$ aproxima desde la derecha$L$, es, o, el límite de la mano derecha de$f$ at$c$ es$L$, denotado por

\[ \lim\limits_{x\rightarrow c^+} f(x) = L,\]

significa que dada alguna$\epsilon > 0$, existe$\delta > 0$ tal que para todos$x> c$, si$|x - c| < \delta$, entonces$|f(x) - L| < \epsilon$.

Prácticamente hablando, al evaluar un límite de la izquierda, consideramos solo valores de$x$ “a la izquierda de”$c$, es decir, dónde$x<c$. La notación ciertamente imperfecta$x\to c^-$ se utiliza para implicar que miramos los valores de$x$ a la izquierda de$c$. La notación no tiene nada que ver con valores positivos o negativos de cualquiera$x$ o$c$. Una afirmación similar se sostiene para evaluar los límites de la mano derecha; ahí consideramos solo valores de$x$ a la derecha de$c$, es decir,$x>c$. Podemos usar los teoremas de secciones anteriores para ayudarnos a evaluar estos límites; simplemente restringimos nuestra visión a un lado de$c$.

Practicamos evaluar los límites de la mano izquierda y derecha mediante una serie de ejemplos.

Ejemplo 17: Evaluación de límites unilaterales

Dejar$ f(x) = \left\{\begin{array}{cc} x & 0\leq x\leq 1 \\ 3-x & 1<x<2\end{array},\right.$ como se muestra en la Figura 1.21. Encuentra cada uno de los siguientes:

$\lim\limits_{x\to 1^-} f(x)$
$\lim\limits_{x\to 1^+} f(x)$
$\lim\limits_{x\to 1} f(x)$
$f(1)$
$\lim\limits_{x\to 0^+} f(x) $
$f(0)$
$\lim\limits_{x\to 2^-} f(x)$
$f(2)$

$alt$
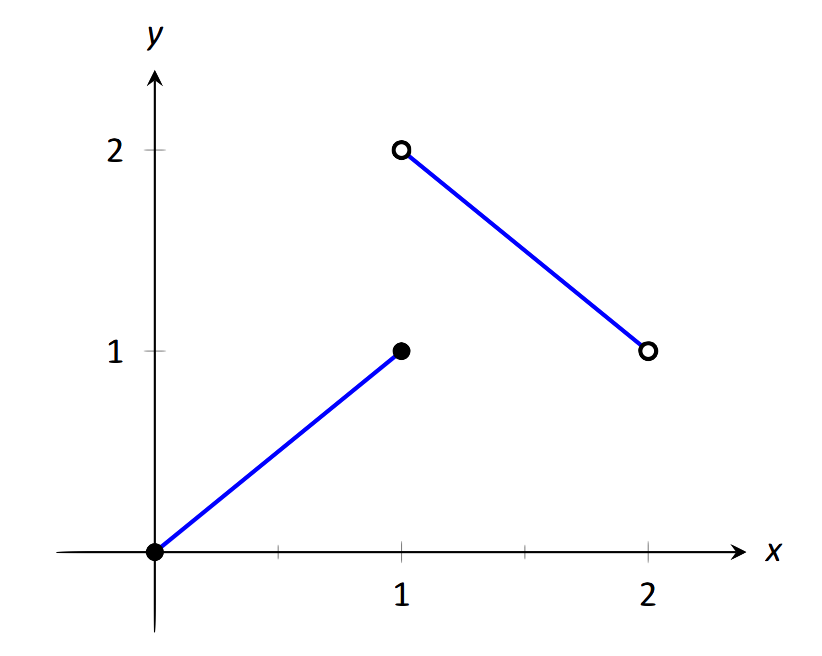
$\text{FIGURE 1.21}$: Una gráfica de$f$ en el Ejemplo 17.

Solución

Para estos problemas, es probable que la ayuda visual de la gráfica sea más efectiva para evaluar los límites que utilizarla a$f$ sí misma. Por lo tanto nos referiremos a menudo a la gráfica.

Al igual que$x$ va a 1 desde la izquierda, vemos que$f(x)$ se acerca al valor de 1. Por lo tanto$ \lim\limits_{x\to 1^-} f(x) =1.$
Al igual que$x$ va a 1 desde la derecha, vemos que$f(x)$ se acerca al valor de 2. Recordemos que no importa que ahí haya un “círculo abierto”; estamos evaluando un límite, no el valor de la función. Por lo tanto$ \lim\limits_{x\to 1^+} f(x)=2$.
El límite de$f$ como$x$ se acerca al 1 no existe, como se discute en el primer apartado. La función no se acerca a un valor en particular, sino a dos valores diferentes desde la izquierda y la derecha.
Usando la definición y al mirar la gráfica vemos eso$f(1) = 1$.
Al igual que$x$ va a 0 desde la derecha, vemos que también$f(x)$ se acerca a 0. Por lo tanto$ \lim\limits_{x\to 0^+} f(x)=0$. Tenga en cuenta que no podemos considerar un límite de la izquierda en 0 ya$f$ que no se define para los valores de$x<0$.
Usando la definición y la gráfica,$f(0) = 0$.
Al igual que$x$ va a 2 desde la izquierda, vemos que$f(x)$ se acerca al valor de 1. Por lo tanto$ \lim\limits_{x\to 2^-} f(x)=1.$
La gráfica y la definición de la función muestran que no$f(2)$ está definida.

Observe cómo los límites de la izquierda y la derecha eran diferentes en$x=1$. Esto, por supuesto, hace que el límite no exista. El siguiente teorema establece lo que es bastante intuitivo: el límite existe precisamente cuando los límites izquierdo y derecho son iguales.

Teorema 7: Límites y Límites unilaterales

Let$f$ Ser una función definida en un intervalo abierto$I$ que contiene$c$. Entonces\[\lim\limits_{x\to c}f(x) = L\] si, y sólo si,\[\lim\limits_{x\to c^-}f(x) = L \quad \text{and} \quad \lim\limits_{x\to c^+}f(x) = L.\]

La frase “si, y sólo si” significa que las dos declaraciones son equivalentes: ambas son verdaderas o ambas falsas. Si el límite es igual$L$, entonces la mano izquierda y derecha limitan ambos iguales$L$. Si el límite no es igual a$L$, entonces al menos uno de los límites izquierdo y derecho no es igual a$L$ (puede que ni siquiera exista).

Una cosa a considerar en los Ejemplos 17 - 20 es que el valor de la función puede/puede no ser igual al valor o valores de sus límites izquierda/derecha, aun cuando estos límites estén de acuerdo.

Ejemplo 18: Evaluación de los límites de una función definida por partes

Dejar$f(x) = \left\{\begin{array}{cc} 2-x & 0<x<1 \\ (x-2)^2 & 1<x<2 \end{array},\right.$ como se muestra en la Figura 1.22. Evalúe lo siguiente.

$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$ f(1)$
$ \lim\limits_{x\to 0^+} f(x)$
$f(0)$
$ \lim\limits_{x\to 2^-} f(x)$
$f(2)$

$alt$
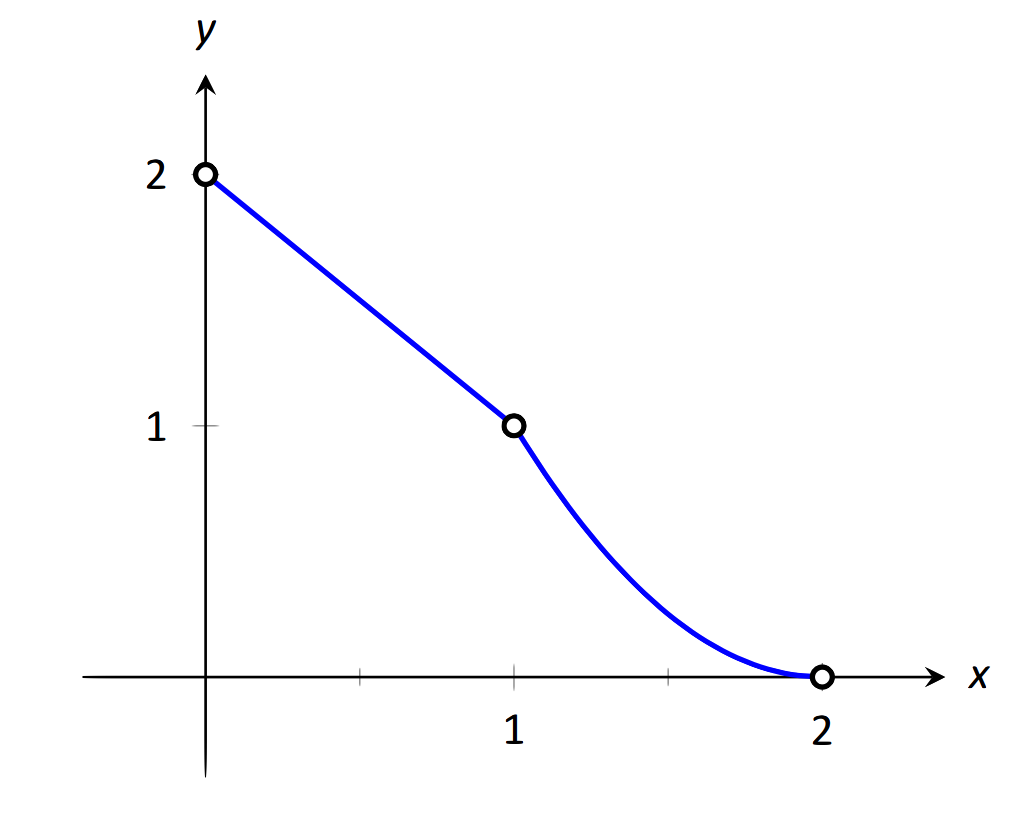
$\text{FIGURE 1.22}$: Una gráfica$f$ del Ejemplo 18.

Solución

Nuevamente evaluaremos cada uno utilizando tanto la definición$f$ de como su gráfica.

A medida que$x$ se acerca a 1 desde la izquierda, vemos que se$f(x)$ acerca a 1. Por lo tanto$ \lim\limits_{x\to 1^-} f(x)=1.$
A medida que$x$ se acerca a 1 desde la derecha, vemos que de nuevo$f(x)$ se acerca a 1. Por lo tanto$ \lim\limits_{x\to 1+} f(x)=1$.
El límite de$f$ como se$x$ acerca a 1 existe y es 1, ya que se$f$ acerca a 1 tanto desde la derecha como desde la izquierda. Por lo tanto$ \lim\limits_{x\to 1} f(x)=1$.
$f(1)$no está definido. Obsérvese que 1 no está en el dominio de$f$ como lo define el problema, que se indica en la gráfica por un círculo abierto cuando$x=1$.
Al igual que$x$ va a 0 desde la derecha,$f(x)$ se acerca a 2. Entonces$ \lim\limits_{x\to 0^+} f(x)=2$.
$f(0)$no se define como no$0$ está en el dominio de$f$.
Al igual que$x$ va a 2 desde la izquierda,$f(x)$ se acerca a 0. Entonces$ \lim\limits_{x\to 2^-} f(x)=0$.
$f(2)$no se define como 2 no está en el dominio de$f$.

Ejemplo 19: Evaluación de los límites de una función definida por partes

Dejar$f(x) = \left\{\begin{array}{cc} (x-1)^2 & 0\leq x\leq 2, x\neq 1\\ 1 & x=1\end{array},\right.$ como se muestra en la Figura 1.23. Evalúe lo siguiente.

$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$

$alt$
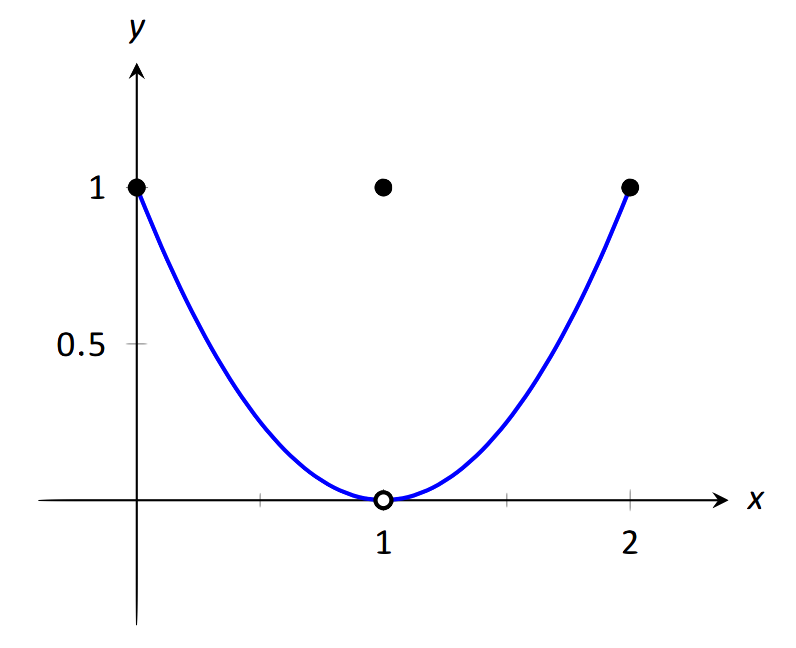
$\text{FIGURE 1.23}$: Graficando$f$ en el Ejemplo 19.

Es claro al mirar la gráfica que tanto los límites de la izquierda como de la derecha de$f$, como se$x$ acerca a 1, es 0. De esta manera también queda claro que el límite es 0; es decir,$ \lim\limits_{x\to 1} f(x) = 0$. También se afirma claramente que$f(1) = 1$.

Ejemplo 20: Evaluación de los límites de una función definida por partes

Dejar$f(x) = \left\{\begin{array}{cc} x^2 & 0\leq x\leq 1 \\ 2-x & 1<x\leq 2\end{array},\right.$ como se muestra en la Figura 1.24. Evalúe lo siguiente.

$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$

$alt$
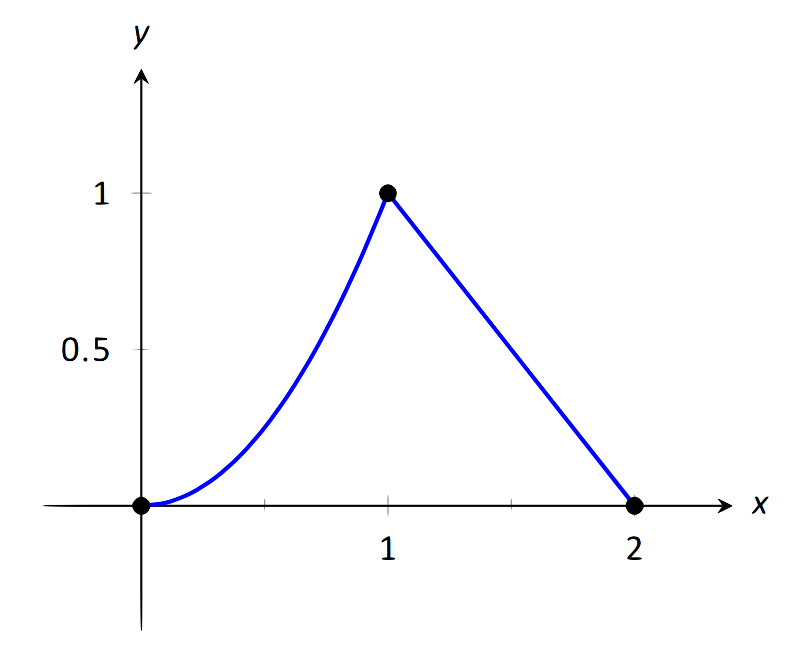
$\text{FIGURE 1.24}$: Graficando$f$ en el Ejemplo 20.

Solución

De la definición de la función y su gráfica queda claro que todos los siguientes son iguales:

\[\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) =\lim\limits_{x\to 1} f(x) =f(1) = 1.\]

En los Ejemplos 17 - 20 nos pidieron que encontráramos ambos$ \lim\limits_{x\to 1}f(x)$ y$f(1)$. Considera la siguiente tabla:

\[\begin{array}{ccc} & \lim\limits_{x\to 1}f(x) & f(1) \\ \hline \text{Example 17} & \text{does not exist} & 1 \\ \text{Example 18} & 1 & \text{not defined} \\ \text{Example 19} & 0 & 1 \\ \text{Example 20} & 1 & 1 \\ \end{array}\]

Sólo en el Ejemplo 20 existen y están de acuerdo tanto la función como el límite. Esto parece “agradable”; de hecho, parece “normal”. De hecho, se trata de una situación importante que exploramos en la siguiente sección, titulada “Continuidad”. En resumen, una función continua es aquella en la que cuando una función se acerca a un valor como$x\rightarrow c$ (es decir, cuándo$ \lim\limits_{x\to c} f(x) = L$), realmente alcanza ese valor en$c$. Tales funciones se comportan muy bien ya que son muy predecibles.

Colaboradores y Atribuciones

Template:ContribApexCalc

Search

Text Color

Text Size

Margin Size

Font Type