1.5: Continuidad

A medida que hemos estudiado los límites, hemos ganado la intuición de que los límites miden ``hacia dónde se dirige una función”. Es decir, si

$$\lim\limits_{x\to 1} f(x) = 3$$

entonces como$x$ está cerca de 1,$f(x)$ está cerca de 3. Hemos visto, sin embargo, que esto no es necesariamente un buen indicador de lo que$f(1)$ realmente es. Esto puede ser problemático; las funciones pueden tender a un valor pero alcanzar otro. Esta sección se centra en las funciones que no exhiben tal comportamiento.

Definición 3 Función continua

Let$f$ Ser una función definida en un intervalo abierto$I$ que contiene$c$.

1. $f$es continuo en$c$ si$\lim\limits_{x\to c}f(x) = f(c)$.
2. $f$es continuo encendido$I$ si$f$ es continuo en$c$ para todos los valores de$c$ in$I$. Si$f$ es continuo$(-\infty,\infty)$, decimos que$f$ es continuo en todas partes.

Una manera útil de establecer si una función$f$ es continua o no en$c$ es verificar las siguientes tres cosas:

1. $\lim\limits_{x\to c} f(x)$existe,
2. $f(c)$se define, y
3. $\lim\limits_{x\to c} f(x) = f(c)$.

Ejemplo 21: Encontrar intervalos de continuidad

$f$Sea definido como se muestra en la Figura 1.25. Dar el (los) intervalo (s) en el que$f$ es continuo.

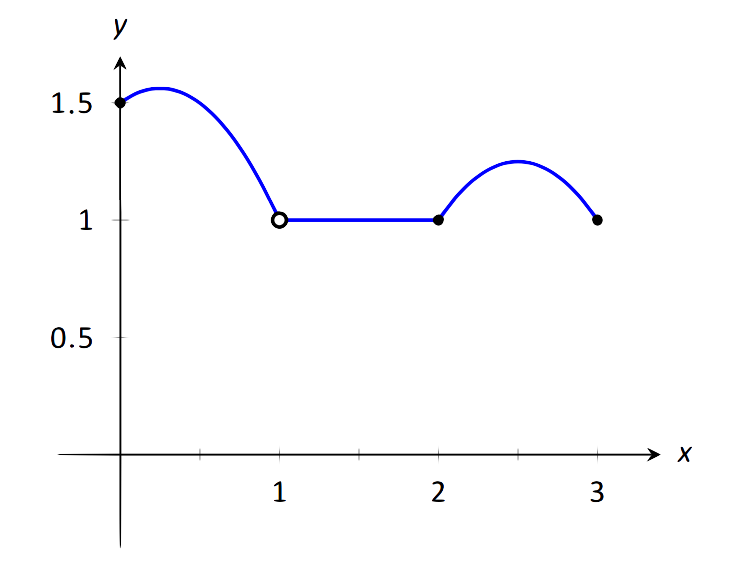
$\text{FIGURE 1.25}$: Una gráfica de$f$ en el Ejemplo 21.

Solución

Se procede examinando los tres criterios de continuidad.

1. Los límites$\lim\limits_{x\to c} f(x)$ existen para todos$c$ entre 0 y 3.
2. $f(c)$se define para todos$c$ entre 0 y 3, excepto para$c=1$. Sabemos de inmediato que$f$ no puede ser continuo en$x=1$.
3. El límite$\lim\limits_{x\to c} f(x) = f(c)$ para todos$c$ entre 0 y 3, excepto, por supuesto, para$c=1$.

Concluimos que$f$ es continuo en cada punto de$(0,3)$ excepto en$x=1$. Por lo tanto$f$ es continuo en$(0,1)\cup(1,3)$.

Ejemplo 22: Encontrar intervalos de continuidad

La función floor,$f(x) = \lfloor x \rfloor$, devuelve el entero más grande menor que la entrada$x$. (Por ejemplo,$f(\pi) = \lfloor \pi \rfloor = 3$.) El gráfico de$f$ la Figura 1.26 demuestra por qué esto a menudo se llama una “función de paso”.

Dar los intervalos en los que$f$ es continuo.

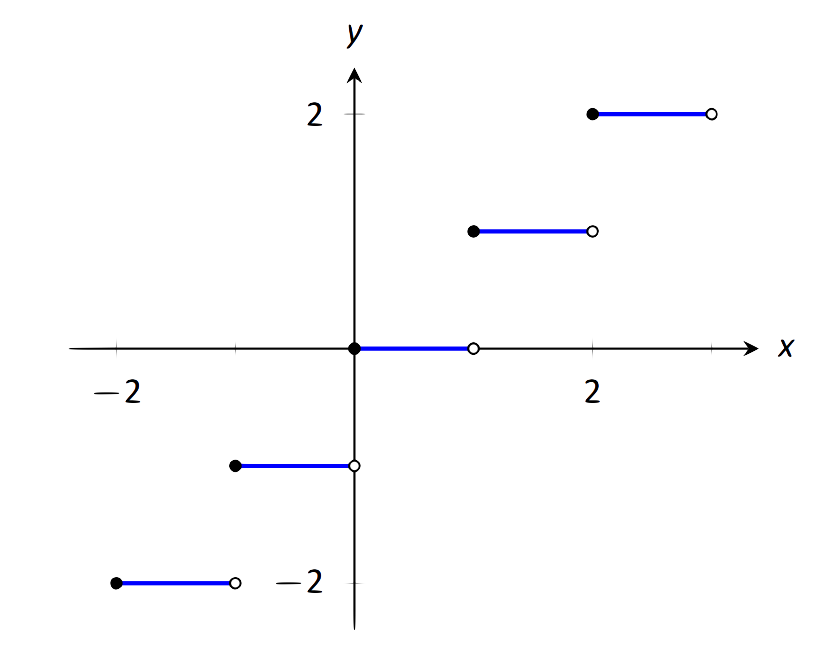
$\text{FIGURE 1.26}$: Un gráfico de la función step en el Ejemplo 22.

Solución

Se examinan los tres criterios de continuidad.

1. Los límites$\lim\limits_{x\to c} f(x)$ no existen en los saltos de un “paso” al siguiente, que ocurren en todos los valores enteros de$c$. Por lo tanto los límites existen para todos$c$ excepto cuando$c$ es un entero.
2. La función se define para todos los valores de$c$.
3. El límite$\lim\limits_{x\to c} f(x) = f(c)$ para todos los valores de$c$ donde exista el límite, ya que cada paso consiste en solo una línea.

Concluimos que$f$ es continuo en todas partes excepto en valores enteros de$c$. Entonces los intervalos en los que$f$ es continuo son $$\ldots, (-2,-1), (-1,0), (0,1), (1,2), \ldots.$$

Nuestra definición de continuidad en un intervalo especifica que el intervalo es un intervalo abierto. Podemos extender la definición de continuidad a intervalos cerrados considerando los límites unilaterales apropiados en los puntos finales.

Definición 4: Continuidad en Intervalos Cerrados

Dejar$f$ ser definido en el intervalo cerrado$[a,b]$ para algunos números reales$a,b$. $f$es continuo$[a,b]$ si:

1. $f$es continuo en$(a,b)$,
2. $\lim\limits_{x\to a^+} f(x) = f(a)$y
3. $\lim\limits_{x\to b^-} f(x) = f(b)$.

Podemos hacer los ajustes adecuados para hablar de continuidad en intervalos medio abiertos como$[a,b)$ o$(a,b]$ si es necesario.

Ejemplo 23: Determinación de intervalos en los que una función es continua

Para cada una de las siguientes funciones, dé el dominio de la función y el (los) intervalo (s) en el que es continua.

1. $f(x) = 1/x$
2. $f(x) = \sin x$
3. $f(x) = \sqrt{x}$
4. $f(x) = \sqrt{1-x^2}$
5. $f(x) = |x|$

Solución

Examinamos cada uno a su vez.

1. El dominio de$f(x) = 1/x$ es$(-\infty,0) \cup (0,\infty)$. Al tratarse de una función racional, aplicamos el Teorema 2 para reconocer que$f$ es continuo en todo su dominio.
2. El dominio de$f(x) = \sin x$ es todo números reales, o$(-\infty,\infty)$. Aplicando el Teorema 3 demuestra que$\sin x$ es continuo en todas partes.
3. El dominio de$f(x) = \sqrt{x}$ es$[0,\infty)$. Aplicando el Teorema 3 muestra que$f(x) = \sqrt{x}$ es continuo en su dominio de$[0,\infty)$.
4. El dominio de$f(x) = \sqrt{1-x^2}$ es$[-1,1]$. Aplicando los Teoremas 1 y 3 demuestra que$f$ es continuo en todo su dominio,$[-1,1]$.
5. El dominio de$f(x) = |x|$ es$(-\infty,\infty)$. Podemos definir la función de valor absoluto como$f(x) = \left\{\begin{array}{cc} -x & x<0 \\ x & x\geq 0\end{array}\right.$. Cada “pieza” de esta función definida por partes es continua en todo su dominio, dando que$f$ es continua en$(-\infty,0)$ y$[0,\infty)$. No podemos asumir que esto implica que$f$ es continuo$(-\infty,\infty)$; necesitamos comprobarlo$\lim\limits_{x\to 0}f(x) = f(0)$, como$x=0$ es el punto en el que$f$ transita de una ``pieza” de su definición a la otra. Es fácil verificar que efectivamente esto es cierto, de ahí que concluyamos que$f(x) = |x|$ es continuo en todas partes.

La continuidad está intrínsecamente ligada a las propiedades de los límites. Debido a esto, las propiedades de límites que se encuentran en los Teoremas 1 y 2 también se aplican a la continuidad. Además, ahora conociendo la definición de continuidad podemos re—leer el Teorema 3 como dando una lista de funciones que son continuas en sus dominios. El siguiente teorema establece cómo las funciones continuas se pueden combinar para formar otras funciones continuas, seguido de un teorema que enumera formalmente funciones que sabemos que son continuas en sus dominios.

Teorema 8: Propiedades de las Funciones Continuas

Dejar$f$ y$g$ ser funciones continuas en un intervalo$I$, dejar$c$ ser un número real y dejar$n$ ser un entero positivo. Las siguientes funciones son continuas$I$.

1. Sumas/Diferencias:$f\pm g$
2. Multiplos Constantes:$c\cdot f$
3. Productos:$f\cdot g$
4. Cocientes:$f/g$ (siempre y cuando$g\neq 0$ encendido$I$)
5. Poderes:$f\,^n$
6. Raíces:$\sqrt[n]{f}$ (si$n$ es par entonces$f\geq 0$ encendido$I$; si$n$ es impar, entonces verdadero para todos los valores de$f$ on$I$.)
7. Composiciones: Ajustar las definiciones de$f$ y$g$ a: Let$f$ be continuous on$I$, donde$I$ está el rango de$f$ on$J$, y let$g$ be continuous on$J$. Entonces$g\circ f$, es decir,$g(f(x))$, es continuo en$I$.

Teorema 9: Funciones continuas

Las siguientes funciones son continuas en sus dominios.

$\begin{align} &1.\, f(x) = \sin x \qquad \qquad \qquad &&2.\, f(x) = \cos x \\ &3.\,f(x) = \tan x &&4.\,f(x) = \cot x \\ &5.\,f(x) = \sec x &&6.\,f(x) = \csc x \\ &7.\,f(x) = \ln x &&8.\,f(x) = \sqrt[n]{x}, \\ &9.\,f(x) = a^x (a>0) &&\,\,\, \text{(where n is a positive integer)} \\ \end{align}$

Aplicamos estos teoremas en el siguiente Ejemplo.

Ejemplo 24: Determinación de intervalos en los que una función es continua

Indicar el (los) intervalo (s) en el que cada una de las siguientes funciones es continua.

$\begin{align}&1.\,\,f(x) = \sqrt{x-1} + \sqrt{5-x} \qquad \qquad \qquad &&3.\,\,f(x) = \tan x \\ &2.\,\,f(x) = x\sin x &&4.\,\, f(x) = \sqrt{\ln x} \\ \end{align}$

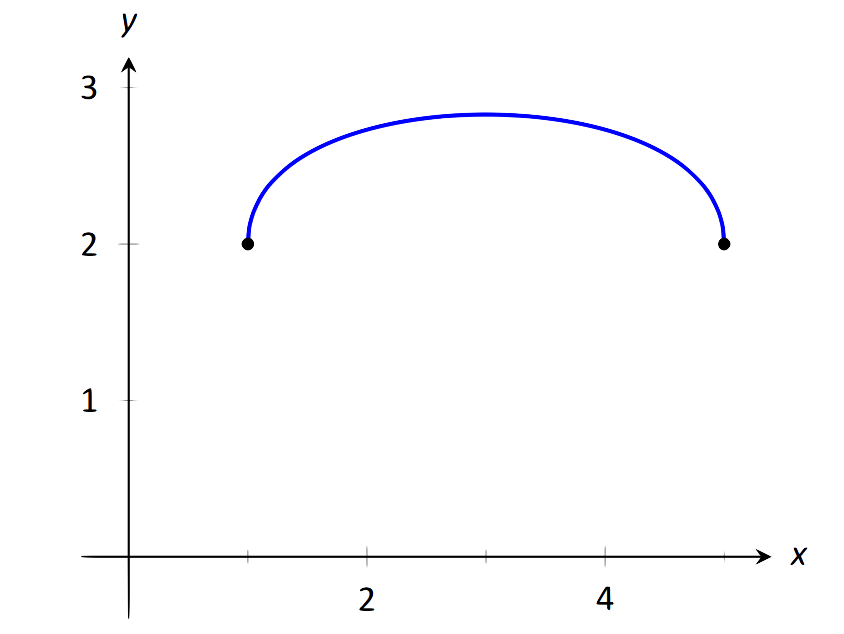
$\text{FIGURE 1.27}$: Un gráfico del$f$ Ejemplo 24 (a).

Solución

Examinamos cada uno a su vez, aplicando los Teoremas 8 y 9 según corresponda.

1. Los términos de raíz cuadrada son continuos en los intervalos$[1,\infty)$ y$(-\infty,5]$, respectivamente. Como$f$ es continuo solo donde cada término es continuo,$f$ es continuo en$[1,5]$, la intersección de estos dos intervalos. En la Figura 1.27$f$ se da una gráfica de.
   
2. Las funciones$y=x$ y$y=\sin x$ son cada una continua en todas partes, de ahí que su producto sea, también.
3. El teorema 9 afirma que$f(x) = \tan x$ es continuo “en su dominio”. Su dominio incluye todos los números reales excepto los múltiplos impares de$\pi/2$. Así$f(x) = \tan x$ es continuo en $$\ldots \left(-\frac{3\pi}{2},-\frac{\pi}2\right),\ \left(-\frac{\pi}2,\frac{\pi}2\right),\ \left(\frac{\pi}2,\frac{3\pi}2\right),\ldots,$$ o, equivalentemente, en$D = \{x\in \mathbb{R}\ |\ x\neq n\cdot \frac{\pi}2,\, \text{n is an odd integer} \}.$
4. El dominio de$y = \sqrt{x}$ es$[0,\infty)$. El rango de$y=\ln x$ es$(-\infty,\infty)$, pero si restringimos su dominio a$[1,\infty)$ su rango es$[0,\infty)$. Por lo que restringir$y = \ln x$ al dominio de$[1,\infty)$ restringe su salida es$[0,\infty)$, sobre la que$y = \sqrt{x}$ se define. Así el dominio de$f(x) = \sqrt{\ln x}$ es$[1,\infty)$.

Una forma común de pensar en una función continua es que “su gráfica se puede esbozar sin levantar el lápiz”. Es decir, su gráfica forma una curva “continua”, sin agujeros, roturas o saltos. Si bien más allá del alcance de este texto, esta pseudodefinición pasa por alto algunos de los puntos más finos de continuidad. Funciones muy extrañas son continuas que uno estaría muy presionado para realmente bosquejar a mano.

Esta noción intuitiva de continuidad nos ayuda a entender otro concepto importante de la siguiente manera. Supongamos que$f$ se define en$[1,2]$ y$f(1) = -10$ y$f(2) = 5$. Si$f$ es continuo$[1,2]$ (es decir, su gráfica se puede esbozar como una curva continua de$(1,-10)$ a$(2,5)$) entonces sabemos intuitivamente que en algún lugar de$[1,2]$$f$ debe ser igual a$-9$$-8$, y, y$-7,\ -6,\ \ldots,\ 0,\ 1/2,$ etc. En definitiva,$f$ toma en todos valores intermedios entre$-10$ y$5$. Puede tomar más valores; en realidad$f$ puede ser igual a 6 en algún momento, por ejemplo, pero se nos garantiza todos los valores entre$-10$ y 5.

Si bien esta noción parece intuitiva, no es trivial de probar y su importancia es profunda. Por lo tanto, el concepto se afirma en forma de teorema.

Teorema 10: Teorema del Valor Intermedio

Que$f$ sea una función continua sobre$[a,b]$ y, sin pérdida de generalidad, dejemos$f(a) < f(b)$. Entonces por cada valor$y$, donde$f(a) < y < f(b)$, hay un valor$c$ en$[a,b]$ tal que$f(c) = y$.

Una aplicación importante del Teorema del Valor Intermedio es el hallazgo raíz. Dada una función$f$, a menudo nos interesa encontrar valores de$x$ dónde$f(x) = 0$. Estas raíces pueden ser muy difíciles de encontrar exactamente. Se pueden encontrar buenas aproximaciones a través de sucesivas aplicaciones de este teorema. Supongamos que a través del cálculo directo nos encontramos con eso$f(a) <0 \( and \(f(b)>0$, dónde$a<b$. El Teorema del Valor Intermedio establece que hay un$c$ en$[a,b]$ tal que$f(c) = 0$. El teorema no nos da ninguna pista de dónde está ese valor en el intervalo$[a,b]$, solo que existe.

Existe una técnica que produce una buena aproximación de$c$. Dejar$d$ ser el punto medio del intervalo$[a,b]$ y considerar$f(d)$. Hay tres posibilidades:

1. $f(d) = 0$— tuvimos suerte y tropezamos con el valor real. Nos detenemos como encontramos una raíz.
2. $f(d) <0$Entonces sabemos que hay una raíz de$f$ en el intervalo$[d,b]$ —hemos reducido a la mitad el tamaño de nuestro intervalo, de ahí que estemos más cerca de una buena aproximación de la raíz.
3. $f(d) >0$Entonces sabemos que hay una raíz de$f$ en el intervalo$[a,d]$ —de nuevo, hemos reducido a la mitad el tamaño de nuestro intervalo, de ahí que estemos más cerca de una buena aproximación de la raíz.

La aplicación sucesiva de esta técnica se denomina Método de Bisección de búsqueda de raíces. Seguimos hasta que el intervalo sea suficientemente pequeño. Esto lo demostramos en el siguiente ejemplo.

Ejemplo 25: Uso del método de bisección

Aproximar la raíz de$f(x) = x-\cos x$, precisa a tres lugares después del decimal.

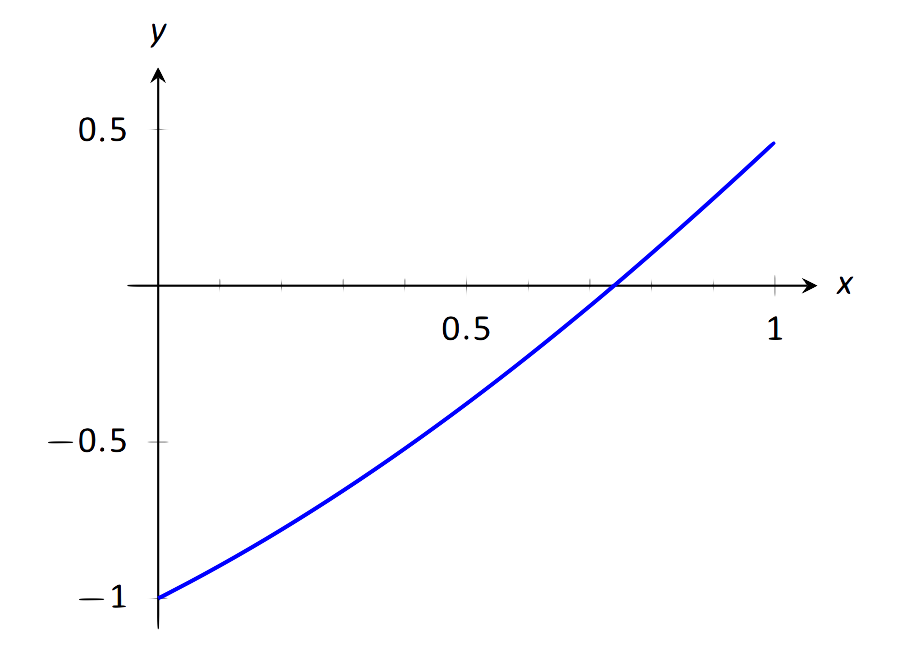
$\text{FIGURE 1.28}$: Graficando una raíz de$f(x) = x-\cos x$.

Solución

Considera la gráfica de$f(x) = x-\cos x$, que se muestra en la Figura 1.28. Es claro que la gráfica cruza el$x$ eje -eje en algún lugar cercano$x=0.8$. Para iniciar el Método de Bisección, elija un intervalo que contenga$0.8$. Nosotros elegimos$[0.7,0.9]$. Tenga en cuenta que todo lo que nos importa son signos de$f(x)$, no su valor real, así que esto es todo lo que mostramos.

1. Iteración 1:$f(0.7) < 0$,$f(0.9) > 0$, y$f(0.8) >0$. Así que reemplace$0.9$ con$0.8$ y repita.
2. Iteración 2:$f(0.7)<0$$f(0.8) > 0$,, y en el punto medio$0.75$,, tenemos$f(0.75) >0$. Así que reemplace$0.8$ con$0.75$ y repita. Tenga en cuenta que no necesitamos continuar verificando los puntos finales, solo el punto medio. Así ponemos el resto de las iteraciones en la Tabla 1.29.

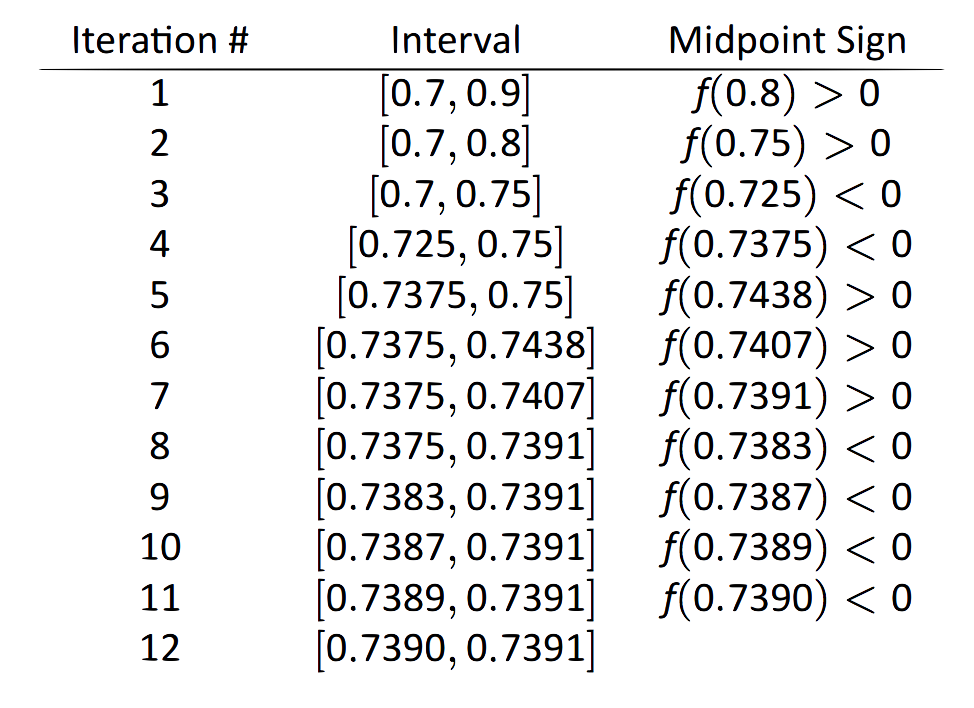
$\text{FIGURE 1.29}$: Iteraciones del método de bisección de búsqueda de raíces

Observe que en la$^\text{th}$ iteración 12 tenemos los endpoints del intervalo cada uno comenzando con$0.739$. Así, hemos reducido el cero a una precisión de los tres primeros lugares después del decimal. Usando una computadora, tenemos

$$f(0.7390) = -0.00014, \quad f(0.7391) = 0.000024.$$ Cualquiera de los extremos del intervalo da una buena aproximación de donde$f$ es 0. El Teorema del Valor Intermedio establece que el cero real aún se encuentra dentro de este intervalo. Si bien no conocemos su valor exacto, sabemos que empieza con$0.739$.

Este tipo de ejercicio rara vez se realiza a mano. Más bien, es sencillo programar una computadora para ejecutar dicho algoritmo y detenerse cuando los puntos finales difieren en una pequeña cantidad preestablecida. Uno de los autores sí escribió dicho programa y encontró que el cero de$f$, exacto a 10 lugares después del decimal, era 0.7390851332. Si bien tardó unos minutos en escribir el programa, tardó menos de una milésima de segundo para que el programa ejecutara las 35 iteraciones necesarias. En menos de 8 centésimas de segundo, el cero se calculó a 100 decimales (con menos de 200 iteraciones).

Es un asunto sencillo extender el Método de Bisección para resolver problemas similares a “Encontrar$x$, dónde”$f(x) = 0$. Por ejemplo, podemos encontrar$x$, dónde$f(x) = 1$. En realidad funciona muy bien para definir una nueva función$g$ donde$g(x) = f(x) - 1$. Después usa el Método de Bisección para resolver$g(x)=0$.

De igual manera, dadas dos funciones$f$ y$g$, podemos usar el Método de Bisección para resolver$f(x) = g(x)$. Una vez más, crear una nueva función$h$ donde$h(x) = f(x)-g(x)$ y resolver$h(x) = 0$.

En la Sección 4.1 se introducirá otro método de resolución de ecuaciones, llamado Método de Newton. En muchos casos, el Método de Newton es mucho más rápido. Se basa en matemáticas más avanzadas, sin embargo, así que esperaremos antes de introducirla.

Esta sección definió formalmente lo que significa ser una función continua. La “mayoría” de las funciones que tratamos son continuas, por lo que a menudo se siente extraño tener que definir formalmente este concepto. Independientemente, es importante, y forma la base del siguiente capítulo.

En la siguiente sección examinamos un aspecto más de los límites: los límites que involucran el infinito.

Colaboradores y Atribuciones

• Template:ContribApexCalc