1.6: Límites que involucran el infinito
- Page ID
- 111873
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la Definición 1 afirmamos que en la ecuación\( \lim\limits_{x\to c}f(x) = L\), ambos\(c\) y\(L\) eran números. En esta sección relajamos un poco esa definición al considerar situaciones en las que tiene sentido dejar\(c\) y/o\(L\) ser “infinito”.
Como ejemplo motivador, consideremos\(f(x) = 1/x^2\), como se muestra en la Figura 1.30. Observe cómo, a medida que\(x\) se acerca a 0,\(f(x)\) crece muy, muy grande. Parece apropiado, y descriptivo, afirmar que\[\lim\limits_{x\rightarrow 0} \frac1{x^2}=\infty.\] También tenga en cuenta que como\(x\) se pone muy grande,\(f(x)\) se pone muy, muy pequeño. Podríamos representar este concepto con notación como\[\lim\limits_{x\rightarrow \infty} \frac1{x^2}=0.\]
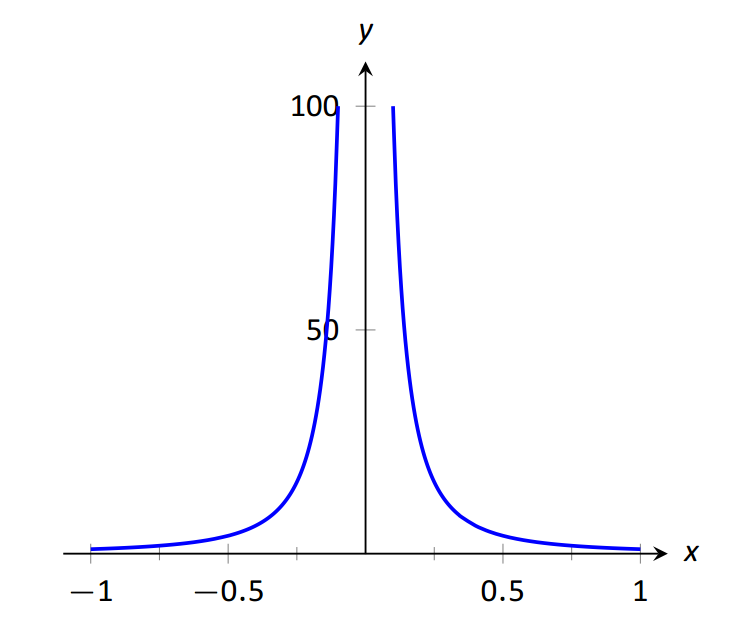
\(\text{FIGURE 1.30}\): Graficando\(f(x)=1/x^2\) para valores de\(x \text{ near }0\).
Exploramos ambos tipos de uso de\(\infty\) a su vez.
Definición 5: Límite de infinito
Decimos\( \lim\limits_{x\rightarrow c} f(x)=\infty\) si por cada\(M>0\) existe\(\delta>0\) tal que para todos\(x\neq c\), si\(|x-c|<\delta\), entonces\(f(x)\geq M\).
Esto es igual que la\(\epsilon\) —\(\delta\) definición de la Sección 1.2. En esa definición, dado cualquier valor (pequeño)\(\epsilon\), si dejamos\(x\) acercarnos lo suficiente a\(c\) (dentro de\(\delta\) unidades de\(c\)) entonces\(f(x)\) se garantiza que esté dentro\(\epsilon\) de\(f(c)\). Aquí, dado cualquier valor (grande)\(M\), si dejamos\(x\) acercarnos lo suficiente a\(c\) (dentro de\(\delta\) unidades de\(c\)), entonces\(f(x)\) será al menos tan grande como\(M\). En otras palabras, si nos acercamos lo suficiente a\(c\), entonces podemos hacer\(f(x)\) lo más grande que queramos. Podemos definir límites iguales a\(-\infty\) de manera similar.
Es importante señalar que al decir\( \lim\limits_{x\to c}f(x) = \infty\) estamos afirmando implícitamente que\ textit {el} límite de\(f(x)\), como\(x\) enfoques\(c\), no existe. Un límite solo existe cuando se\(f(x)\) acerca a un valor numérico real. Utilizamos el concepto de límites que se acercan al infinito porque es útil y descriptivo.
Ejemplo 26: Evaluar límites que involucran infinito
Encuentre\( \lim\limits_{x\rightarrow 1}\frac1{(x-1)^2}\) como se muestra en la Figura 1.31.
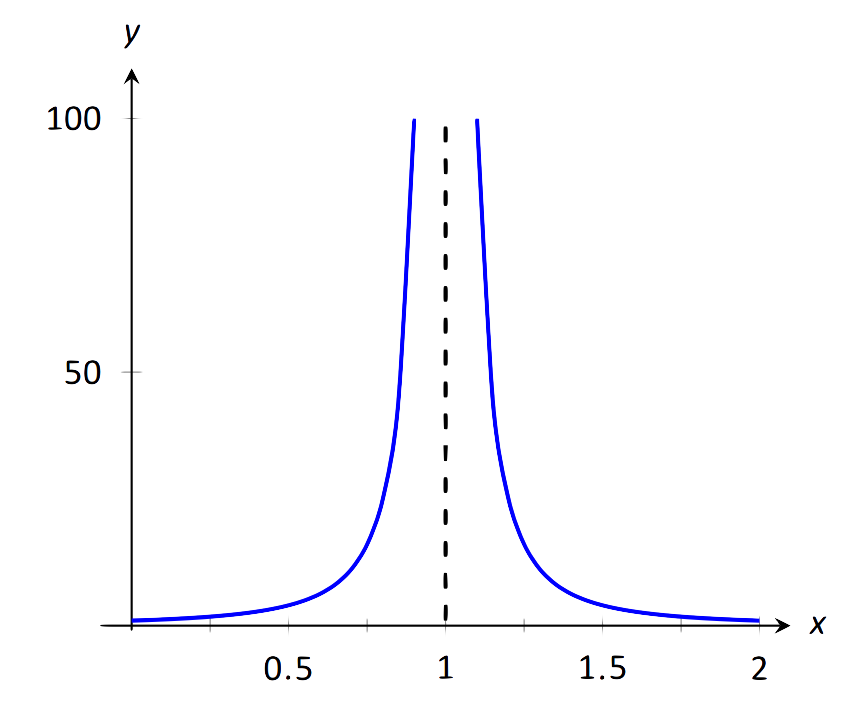
\(\text{FIGURE 1.31}\): Observando el límite infinito como\(x\to 1\) en el Ejemplo 26.
Solución
En el Ejemplo 4 de la Sección 1.1, al inspeccionar valores\(x\) cercanos al 1 concluimos que este límite no existe. Es decir, no puede igualar ningún número real. Pero el límite podría ser infinito. Y de hecho, vemos que la función sí parece estar creciendo cada vez más grande, como\(f(.99)=10^4\),\(f(.999)=10^6\),\(f(.9999)=10^8\). Algo similar sucede en el otro lado de 1. En general, dejar que se le dé un valor\(M\) “grande”. Vamos\(\delta=1/\sqrt{M}\). Si\(x\) está dentro\(\delta\) de 1, es decir, si\(|x-1|<1/\sqrt{M}\), entonces:
\[\begin{align*}|x-1| &< \frac{1}{\sqrt{M}} \\ (x-1)^2 &< \frac{1}{M}\\ \frac{1}{(x-1)^2} &> M,\end{align*}\]
que es lo que queríamos mostrar. Entonces podemos decir\(\lim\limits_{x\rightarrow 1}1/{(x-1)^2}=\infty\).
Ejemplo 27: Evaluar límites que involucran infinito
Encuentre\(\lim\limits_{x\rightarrow 0}\frac1x\), como se muestra en la Figura 1.32.
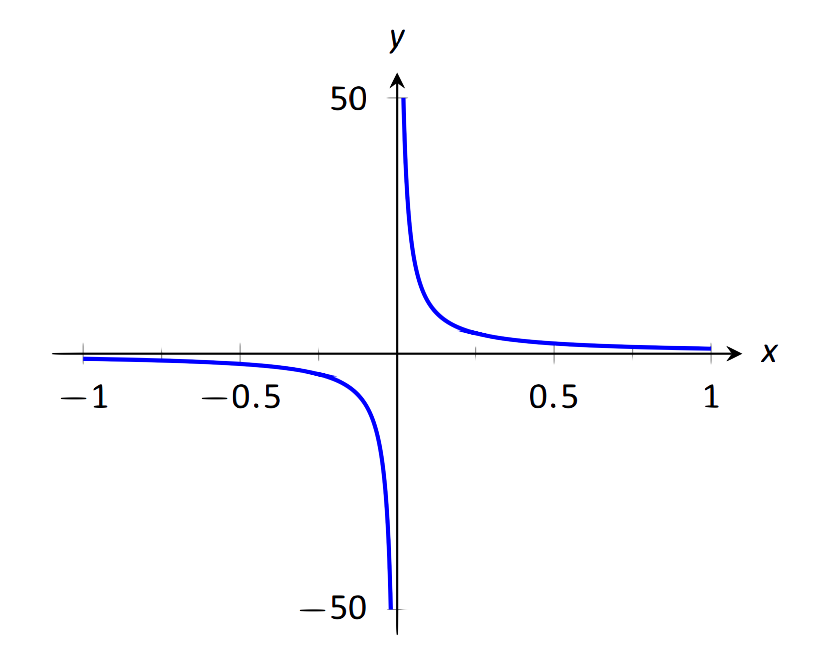
\(\text{FIGURE 1.32}\): Evaluando\(\lim\limits_{x\to 0}\frac{1}{x}\).
Solución
Es fácil ver que la función crece sin límite cerca de 0, pero lo hace de diferentes maneras en diferentes lados de 0. Dado que su comportamiento no es consistente, no podemos decir eso\( \lim\limits_{x\to 0}\frac{1}{x}=\infty\). Sin embargo, podemos hacer una declaración sobre los límites unilaterales. Podemos afirmar que\( \lim\limits_{x\rightarrow 0^+}\frac1x=\infty\) y\( \lim\limits_{x\rightarrow 0^-}\frac1x=-\infty\).
Asintotas verticales
Si el límite de\(f(x)\) as\(x\) se acerca\(c\) desde la izquierda o la derecha (o ambos) es\(\infty\) o\(-\infty\), decimos que la función tiene una asíntota vertical en\(c\).
Ejemplo 28: Encontrar asíntotas verticales
Encuentra las asíntotas verticales de\(f(x)=\dfrac{3x}{x^2-4}\).
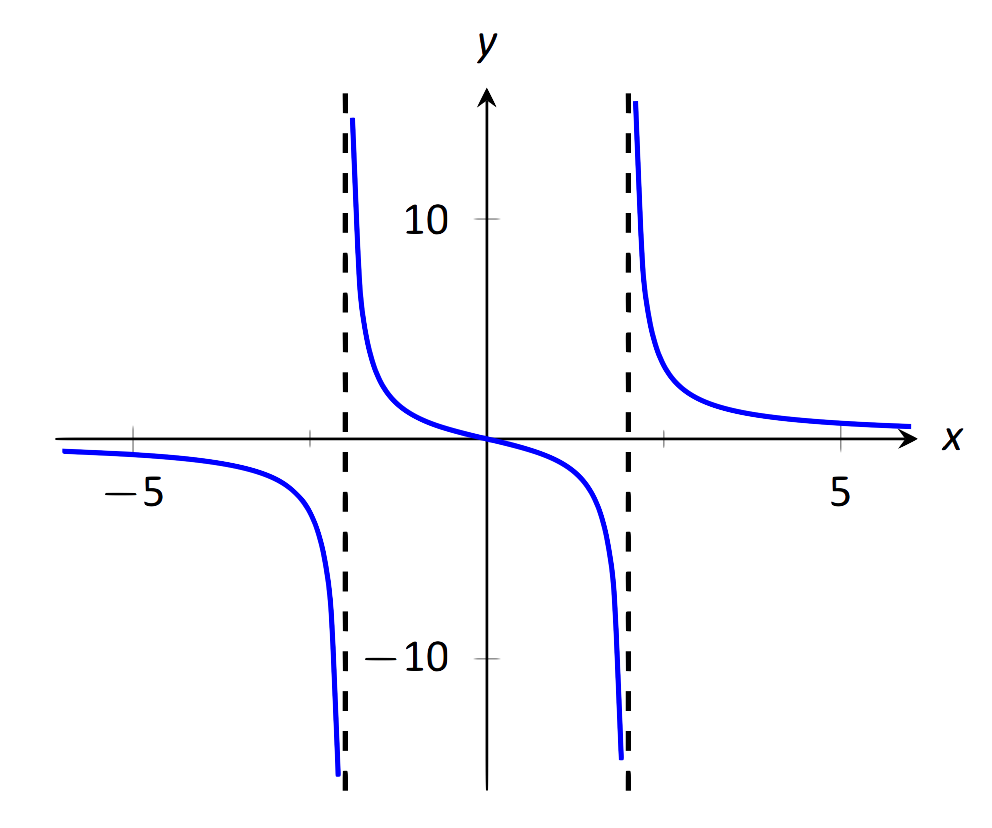
\(\text{FIGURE 1.33}\): Graficar\(f(x) = \frac{3x}{x^2-4}\).
Solución
Las asíntotas verticales ocurren donde la función crece sin límite; esto puede ocurrir en valores\(c\) donde el denominador es 0. Cuando\(x\) está cerca\(c\), el denominador es pequeño, lo que a su vez puede hacer que la función tome valores grandes. En el caso de la función dada, el denominador es 0 at\(x=\pm 2\). Sustituir en valores de\(x\) cercano a\(2\) y\(-2\) parece indicar que la función tiende hacia\(\infty\) o\(-\infty\) en esos puntos. Esto lo podemos confirmar gráficamente observando la Figura 1.33. Así las asíntotas verticales están en\(x=\pm2\).
Cuando una función racional tiene una asíntota vertical at\(x=c\), podemos concluir que el denominador es 0 at\(x=c\). No obstante, el hecho de que el denominador sea 0 en cierto punto no significa que ahí haya una asíntota vertical. Por ejemplo,\(f(x)=(x^2-1)/(x-1)\) no tiene una asíntota vertical en\(x=1\), como se muestra en la Figura 1.34. Mientras que el denominador sí se acerca pequeño\(x=1\), el numerador también se vuelve pequeño, coincidiendo con el denominador paso por paso. De hecho, factorizando el numerador, obtenemos\[f(x)=\frac{(x-1)(x+1)}{x-1}.\]
Cancelando el término común, lo conseguimos\(f(x)=x+1\) para\(x\not=1\). Entonces claramente no hay asíntota, más bien existe un agujero en la gráfica en\(x=1\).
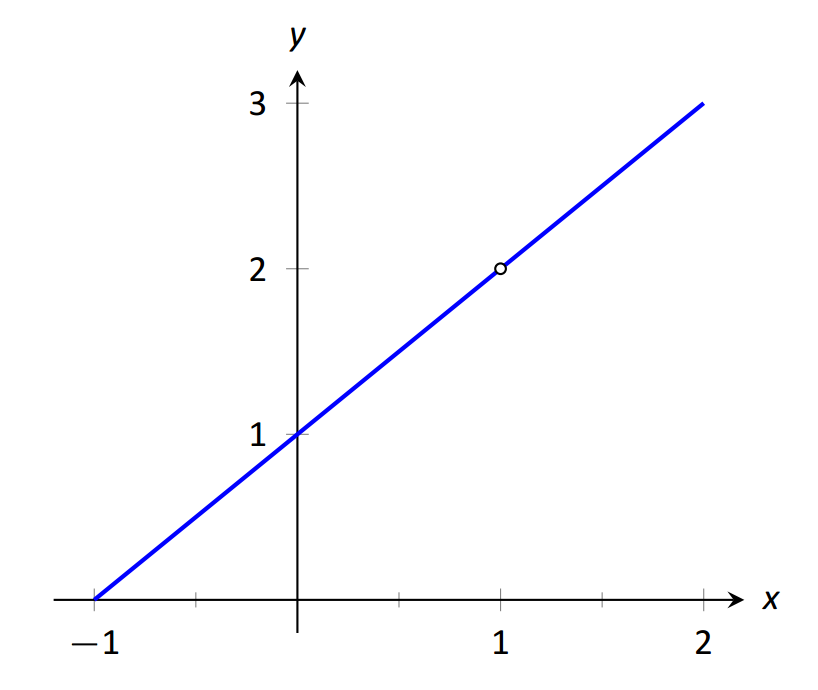
\(\text{FIGURE 1.34}\): Demostrando gráficamente que\(f(x)=\frac{x^2-1}{x-1}\) no tiene una asíntota en\(x=1\).
El ejemplo anterior puede parecer un poco ideado. Otro ejemplo que demuestra este importante concepto es\(f(x)= (\sin x)/x\). Hemos considerado esta función varias veces en los apartados anteriores. Encontramos que\( \lim\limits_{x\to0}\frac{\sin x}{x}=1\); es decir, no hay asíntota vertical. Ninguna simple cancelación algebraica hace que este hecho sea obvio; utilizamos el Teorema de Squeeze en la Sección 1.3 para demostrarlo.
Si el denominador es 0 en cierto punto pero el numerador no lo es, entonces normalmente habrá una asíntota vertical en ese punto. Por otra parte, si el numerador y el denominador son ambos cero en ese punto, entonces puede haber o no una asíntota vertical en ese punto. Este caso donde el numerador y el denominador son ambos cero nos devuelve a un tema importante.
Formularios indeterminados
Hemos visto cómo los límites
\[\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}\quad \text{and}\quad \lim\limits_{x\to1}\frac{x^2-1}{x-1}\]cada uno devuelve la forma indeterminada "\(0/0\)" cuando conectamos ciegamente\(x=0\) y\(x=1\), respectivamente. Sin embargo, no\(0/0\) es una expresión aritmética válida. No da ninguna indicación de que los límites respectivos sean 1 y 2.
Con un poco de astucia, uno puede llegar a\(0/0\) expresiones que tienen un límite de\(\infty\), 0, o cualquier otro número real. Es por ello que a esta expresión se le llama indeterminada.
Un concepto clave a entender es que tales límites realmente no regresan\(0/0\). Más bien, ten en cuenta que estamos tomando límites. Lo que realmente está sucediendo es que el numerador se está reduciendo a 0 mientras que el denominador también se está reduciendo a 0. Las tasas respectivas a las que hacen esto son muy importantes y determinan el valor real del límite.
Una forma indeterminada indica que se necesita hacer más trabajo para poder calcular el límite. Ese trabajo puede ser algebraico (como factorizar y cancelar) o puede requerir una herramienta como el Teorema de Squeeze. En una sección posterior aprenderemos una técnica llamada Regla de l'Hospital's que proporciona otra forma de manejar formas indeterminadas.
Algunas otras formas indeterminadas comunes son\(\infty-\infty\),\(\infty\cdot 0\)\(\infty/\infty\),\(0^0\),\(\infty^0\) y\(1^{\infty}\). Nuevamente, hay que tener en cuenta que estos son los resultados “ciegos” de evaluar un límite, y cada uno, en y por sí mismo, no tiene sentido. La expresión\(\infty-\infty\) no significa realmente “restar el infinito del infinito”. Más bien, significa “Una cantidad se resta de la otra, pero ambas están creciendo sin ataduras”. ¿Cuál es el resultado? Es posible obtener todos los valores entre\(-\infty\) y\(\infty\)
Tenga en cuenta que\(1/0\) y no\(\infty/0\) son formas indeterminadas, aunque tampoco son expresiones matemáticas exactamente válidas. En cada uno, la función está creciendo sin límite, lo que indica que el límite será\(\infty\)\(-\infty\), o simplemente no existirá si los límites izquierdo y derecho no coinciden.
Límites en el infinito y asíntotas horizontales
Al inicio de esta sección consideramos brevemente lo que sucede a\(f(x) = 1/x^2\) medida que\(x\) creció muy grande. Gráficamente, se refiere al comportamiento de la función a la “extrema derecha” de la gráfica. Hacemos esta noción más explícita en la siguiente definición.
Definición 6: Límites en el infinito y asíntota horizontal
- Decimos\(\lim\limits_{x\rightarrow\infty} f(x)=L\) si por cada\(\epsilon>0\) existe\(M>0\) tal que si\(x\geq M\), entonces\(|f(x)-L|<\epsilon\).
- Decimos\(\lim\limits_{x\rightarrow-\infty} f(x)=L\) si por cada\(\epsilon>0\) existe\(M<0\) tal que si\(x\leq M\), entonces\(|f(x)-L|<\epsilon\).
- Si\(\lim\limits_{x\rightarrow\infty} f(x)=L\) o\(\lim\limits_{x\rightarrow-\infty} f(x)=L\), decimos que\(y=L\) es una asíntota horizontal de\(f\).
También podemos definir límites como\(\lim\limits_{x\rightarrow\infty}f(x)=\infty\) por ejemplo combinando esta definición con la Definición 5.
Ejemplo 29: Aproximación de asíntotas horizontales
Aproximar la asíntota (s) horizontal (s) de\( f(x)=\frac{x^2}{x^2+4}\).
Solución
Aproximaremos las asíntotas horizontales aproximando los límites La\[\lim\limits_{x\to-\infty} \frac{x^2}{x^2+4}\quad \text{and}\quad \lim\limits_{x\to\infty} \frac{x^2}{x^2+4}.\] figura 1.35 (a) muestra un boceto de\(f\), y la parte (b) da valores de\(f(x)\) para valores de gran magnitud de\(x\). Parece razonable concluir de ambas fuentes que\(f\) tiene una asíntota horizontal en\(y=1\).
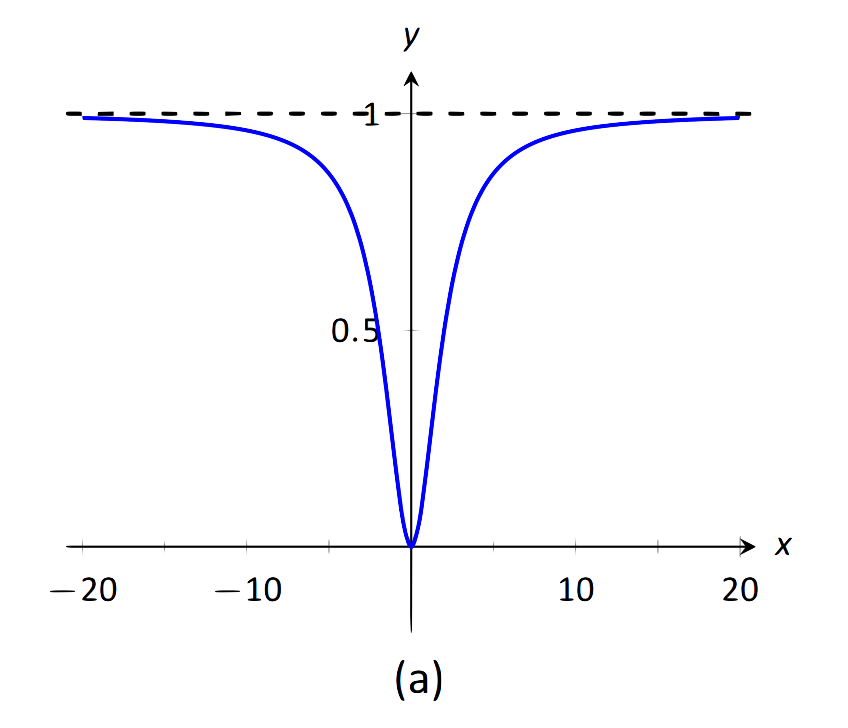
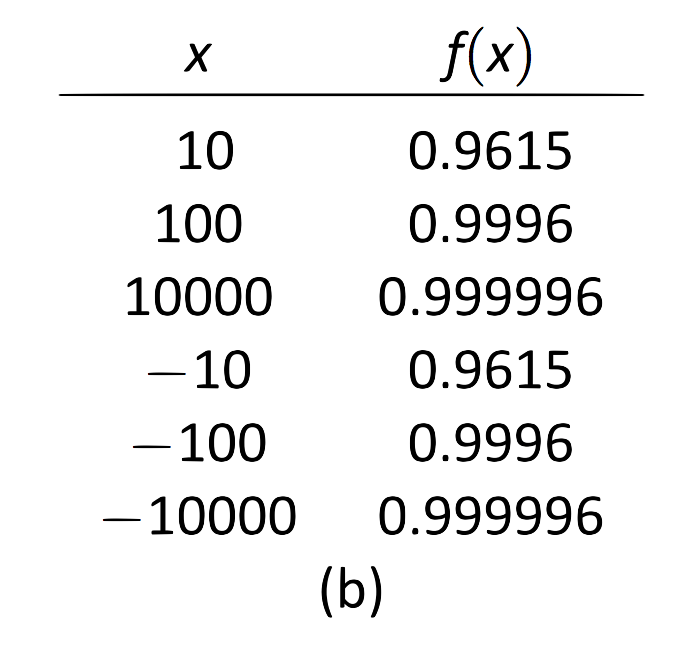
\(\text{FIGURE 1.35}\): Usando una gráfica y una tabla para aproximar una asíntota horizontal en el Ejemplo 29.
Posteriormente, mostraremos cómo determinarlo analíticamente.
Las asíntotas horizontales pueden tomar una variedad de formas. La figura 1.36 (a) muestra que\(f(x) = x/(x^2+1)\) tiene una asíntota horizontal de\(y=0\), donde 0 se aproxima tanto desde arriba como desde abajo.
La Figura 1.36 (b) muestra que\(f(x) =x/\sqrt{x^2+1}\) tiene dos asíntotas horizontales; una en\(y=1\) y la otra en\(y=-1\).
La Figura 1.36 (c) muestra que\(f(x) = (\sin x)/x\) tiene un comportamiento aún más interesante que en solo\(x=0\); a medida que\(x\) se acerca\(\pm\infty\),\(f(x)\) se acerca a 0, pero oscila a medida que lo hace.
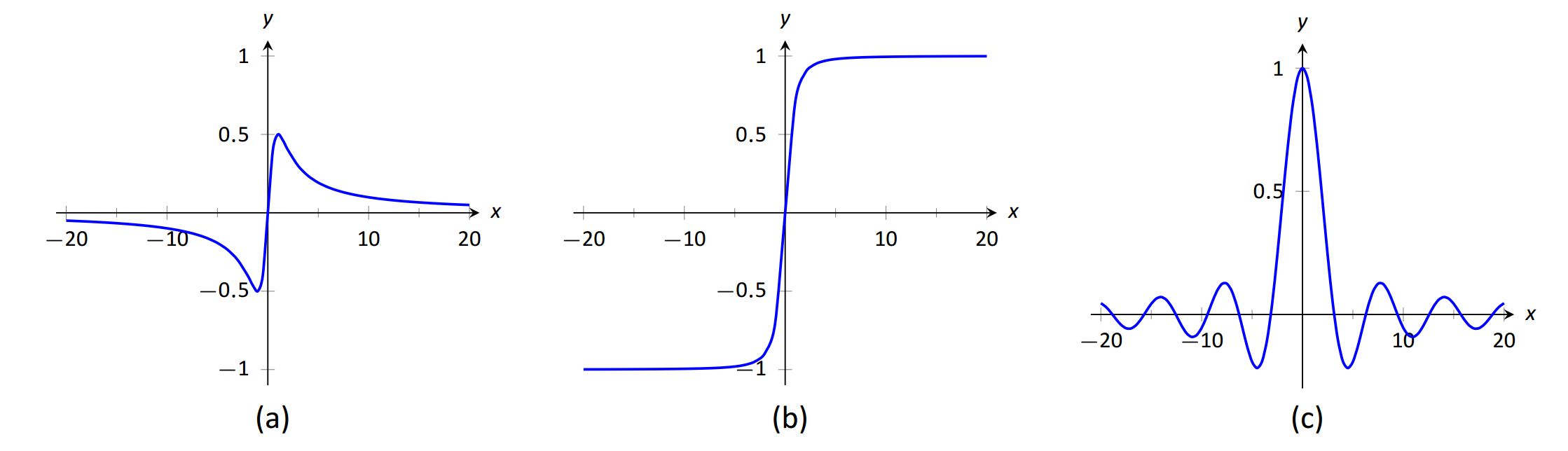
\(\text{FIGURE 1.36}\): Considerando diferentes tipos de asíntotas horizontales.
Podemos evaluar analíticamente límites en el infinito para funciones racionales una vez que entendemos\(\lim\limits_{x\rightarrow\infty} 1/x\). A medida que\(x\) se hace cada vez más grande, el\(1/x\) se hace cada vez más pequeño, acercándose a Podemos, de hecho, hacer\(1/x\) lo pequeño que queramos eligiendo un valor suficientemente grande de\(x\). Dado\(\epsilon\), podemos hacer\(1/x<\epsilon\) eligiendo\(x>1/\epsilon\). Así tenemos\(\lim\limits_{x\rightarrow\infty} 1/x=0\).
Ahora no es un gran salto concluir lo siguiente:
\[\lim\limits_{x\rightarrow\infty}\frac1{x^n}=0\quad \text{and}\quad \lim\limits_{x\rightarrow-\infty}\frac1{x^n}=0\]
Ahora supongamos que necesitamos calcular el siguiente límite:
\[\lim\limits_{x\rightarrow\infty}\frac{x^3+2x+1}{4x^3-2x^2+9}.\]
Una buena manera de abordar esto es dividir a través del numerador y denominador por\(x^3\) (de ahí dividiendo por 1), que es el mayor\(x\) poder de aparecer en la función. Haciendo esto, obtenemos
\[\begin{align*}\lim\limits_{x\rightarrow\infty}\frac{x^3+2x+1}{4x^3-2x^2+9} &=\lim\limits_{x\rightarrow\infty}\frac{1/x^3}{1/x^3}\cdot\frac{x^3+2x+1}{4x^3-2x^2+9}\\ &=\lim\limits_{x\rightarrow\infty}\frac{x^3/x^3+2x/x^3+1/x^3}{4x^3/x^3-2x^2/x^3+9/x^3}\\ &= \lim\limits_{x\rightarrow\infty}\frac{1+2/x^2+1/x^3}{4-2/x+9/x^3}.\end{align*}\]
Luego usando las reglas para los límites (que también mantienen para los límites en el infinito), así como el hecho sobre los límites de\(1/x^n\), vemos que el límite se convierte\[\frac{1+0+0}{4-0+0}=\frac14.\]
Este procedimiento funciona para cualquier función racional. De hecho, nos da el siguiente teorema.
Teorema 11: Límites de las Funciones Racionales al Infinito
Dejar\(f(x)\) ser una función racional de la siguiente forma:
\[f(x)=\frac{a_nx^n + a_{n-1}x^{n-1}+\dots + a_1x + a_0}{b_mx^m + b_{m-1}x^{m-1} + \dots + b_1x + b_0},\]
donde cualquiera de los coeficientes puede ser 0 excepto\(a_n\) y\(b_m\).
- Si\(n=m\), entonces\(\lim\limits_{x\rightarrow\infty} f(x) = \lim\limits_{x\rightarrow-\infty} f(x) = \frac{a_n}{b_m}\).
- Si\(n<m\), entonces\(\lim\limits_{x\rightarrow\infty} f(x) = \lim\limits_{x\rightarrow-\infty} f(x) = 0\).
- Si\(n>m\), entonces\(\lim\limits_{x\rightarrow\infty} f(x)\) y ambos\(\lim\limits_{x\rightarrow-\infty} f(x)\) son infinitos.
Podemos ver por qué esto es cierto. Si la mayor potencia de\(x\) es la misma tanto en el numerador como en el denominador (i.e.\(n=m\)), estaremos en una situación como la del ejemplo anterior, donde dividiremos por\(x^n\) y en el límite todos los términos se acercarán a 0 excepto por\(a_nx^n/x^n\) y\(b_mx^m/x^n\). Ya que\(n=m\), esto nos dejará con el límite\(a_n/b_m\). Si\(n<m\), entonces después de dividir por\(x^m\), todos los términos en el numerador se acercarán a 0 en el límite, dejándonos con\(0/b_m\) o 0. Si\(n>m\), e intentamos dividirnos por\(x^n\), terminamos con todos los términos en el denominador tendiendo hacia 0, mientras que el\(x^n\) término en el numerador no se acerca a 0. Esto es indicativo de algún tipo de límite infinito.
Intuitivamente, como\(x\) se vuelve muy grande, todos los términos en el numerador son pequeños en comparación con\(a_nx^n\), e igualmente todos los términos en el denominador son pequeños comparados con\(b_nx^m\). Si\(n=m\), mirando sólo estos dos términos importantes, tenemos\((a_nx^n)/(b_nx^m)\). Esto reduce a\(a_n/b_m\). Si\(n<m\), la función se comporta como\(a_n/(b_mx^{m-n})\), que tiende hacia 0. Si\(n>m\), la función se comporta como\(a_nx^{n-m}/b_m\), que tenderá a cualquiera\(\infty\) o\(-\infty\) dependiendo de los valores de\(n\)\(m\),\(a_n\),,\(b_m\) y si estás buscando\(\lim\limits_{x\rightarrow\infty} f(x)\) o\(\lim\limits_{x\rightarrow-\infty} f(x)\).
Con cuidado, podemos evaluar rápidamente los límites al infinito para una gran cantidad de funciones al considerar los mayores poderes de\(x\). Por ejemplo, considere nuevamente\(\lim\limits_{x\to\pm\infty}\frac{x}{\sqrt{x^2+1}},\) graficado en la Figura\ ref {fig:hzasy} (b). Cuando\(x\) es muy grande,\(x^2+1 \approx x^2\). Así\[\sqrt{x^2+1}\approx \sqrt{x^2} = |x|,\quad \text{and}\quad \frac{x}{\sqrt{x^2+1}} \approx \frac{x}{|x|}.\] Esta expresión es 1 cuando\(x\) es positiva y\(-1\) cuando\(x\) es negativa. De ahí que obtengamos asíntotas de\(y=1\) y\(y=-1\), respectivamente.
Ejemplo 30: Encontrar un límite de una función racional
Confirmar analíticamente que\(y=1\) es la asíntota horizontal de\( f(x) = \frac{x^2}{x^2+4}\), como se aproxima en el Ejemplo 29.
Solución
Antes de usar el Teorema 11, usemos la técnica de evaluar límites al infinito de funciones racionales que llevaron a ese teorema. El mayor poder de\(x\) in\(f\) es 2, así que divide el numerador y denominador de\(f\) por\(x^2\), luego toma límites.
\[\begin{align*}\lim\limits_{x\to\infty}\frac{x^2}{x^2+4} &= \lim\limits_{x\to\infty}\frac{x^2/x^2}{x^2/x^2+4/x^2}\\ &=\lim\limits_{x\to\infty}\frac{1}{1+4/x^2}\\ &=\frac{1}{1+0}\\ &= 1. \end{align*}\]
También podemos usar directamente el Teorema 11; en este caso\(n=m\) así el límite es la relación de los coeficientes principales del numerador y denominador, es decir, 1/1 = 1.
Ejemplo 31: Encontrar límites de funciones racionales
Utilice el Teorema 11 para evaluar cada uno de los siguientes límites.
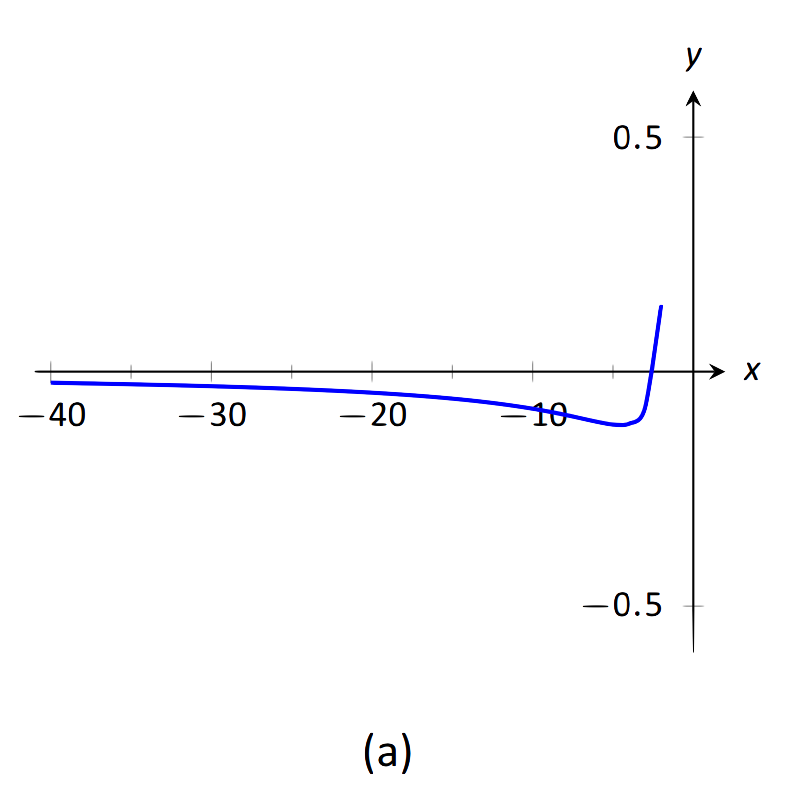
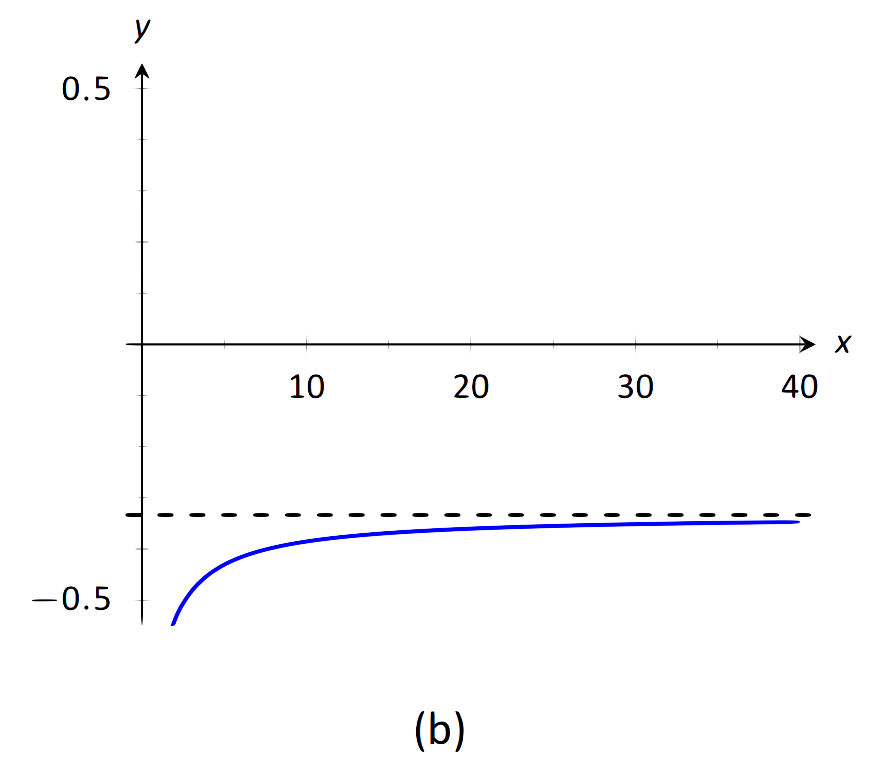
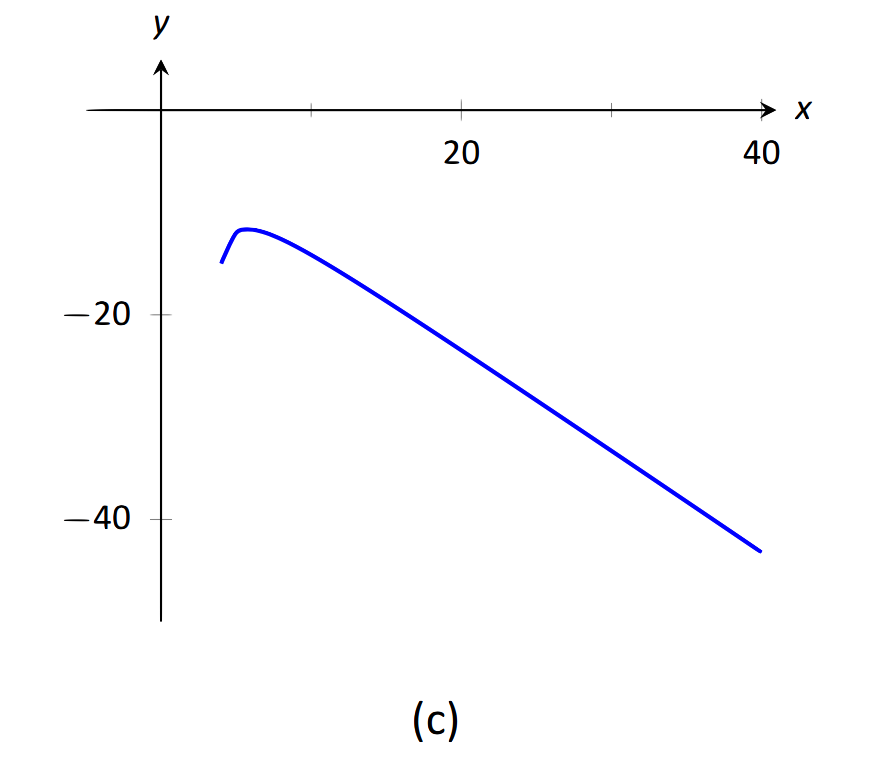
\(\begin{align}&1.\,\,\lim\limits_{x\rightarrow-\infty}\frac{x^2+2x-1}{x^3+1} \qquad\qquad &&3.\,\,\lim\limits_{x\rightarrow\infty}\frac{x^2-1}{3-x} \\ &2.\,\,\lim\limits_{x\rightarrow\infty}\frac{x^2+2x-1}{1-x-3x^2} && \\ \end{align}\)
\(\text{FIGURE 1.37}\): Visualizando las funciones en el Ejemplo 31.
Solución
- El poder más alto de\(x\) está en el denominador. Por lo tanto, el límite es 0; véase la Figura 1.37 (a).
- El poder más alto de\(x\) is\(x^2\), que ocurre tanto en el numerador como en el denominador. El límite es por lo tanto la relación de los coeficientes de\(x^2\), que es\(-1/3\). Ver Figura 1.37 (b).
- El mayor poder de\(x\) está en el numerador por lo que el límite será\(\infty\) o\(-\infty\). Para ver cual, considerar sólo los términos dominantes del numerador y denominador, que son\(x^2\) y\(-x\). La expresión en el límite se comportará como\(x^2/(-x) = -x\) para grandes valores de\(x\). Por lo tanto, el límite es\(-\infty\). Ver Figura 1.37 (c).
Resumen del Capítulo
En este capítulo nosotros:
- definió el límite,
- encontraron formas accesibles de aproximar sus valores numérica y gráficamente,
- desarrolló un método no tan fácil para probar el valor de un límite (\(\epsilon-\delta\)pruebas),
- explorado cuando no existen límites,
- continuidad definida y propiedades exploradas de funciones continuas, y
- consideró límites que implicaban el infinito.
¿Por qué? Las matemáticas son famosas por construir sobre sí mismas y el cálculo no demuestra ser la excepción. En el siguiente capítulo nos interesará “dividir por 0”. Es decir, vamos a querer dividir una cantidad por un número cada vez menor y ver a qué valor se acerca el cociente. En otras palabras, vamos a querer encontrar un límite. Estos límites nos permitirán, entre otras cosas, determinar exactamente qué tan rápido se mueve algo cuando solo se nos da información de posición.
Posteriormente, vamos a querer sumar una lista infinita de números. Lo haremos sumando primero una lista finita de números, luego tomaremos un límite a medida que el número de cosas que estamos sumando se acerca al infinito. Sorprendentemente, esta suma suele ser finita; es decir, podemos sumar una lista infinita de números y obtener, por ejemplo, 42.
Estos son solo dos ejemplos rápidos de por qué nos interesan los límites. A muchos estudiantes no les gusta este tema cuando se les presenta por primera vez, pero con el tiempo a menudo se forma una apreciación basada en el alcance de su aplicabilidad.


