3.3: Funciones crecientes y decrecientes
- Page ID
- 111783
Nuestro estudio de las funciones “agradables”\(f\) en este capítulo se ha centrado hasta ahora en puntos individuales: puntos donde\(f\) es máximo/mínimo, puntos donde\(f'(x) = 0\) o\(f'\) no existe, y puntos\(c\) donde\(f'(c)\) está la tasa promedio de cambio de\(f\) en algún intervalo.
En esta sección comenzamos a estudiar cómo se comportan las funciones entre puntos especiales; comenzamos a estudiar con más detalle la forma de sus gráficas.
Comenzamos con un concepto intuitivo. Dada la gráfica de la Figura\(\PageIndex{1}\), ¿dónde dirías que la función va en aumento? ¿Disminuyendo?
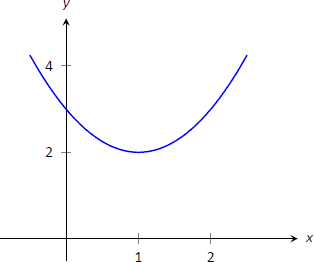
Figura\(\PageIndex{1}\): Gráfica de una función\(f\) utilizada para ilustrar los conceptos de aumento y disminución.
A pesar de que no hemos definido matemáticamente estos términos, uno probablemente respondió que\(f\) está aumentando cuando\(x>1\) y disminuyendo cuando\(x<1\). Aquí definimos formalmente estos términos.
Definición: Funciones crecientes y decrecientes
Let\(f\) Ser una función definida en un intervalo\(I\). \ index {función creciente}\ index {función decreciente}\ index {función creciente! estrictamente}\ index {función decreciente! estrictamente}
- \(f\)está aumentando en\(I\) si por cada\(a<b\) en\(I\),\(f(a) \leq f(b)\).
- \(f\)está disminuyendo en\(I\) si por cada\(a<b\) en\(I\),\(f(a) \geq f(b)\).
Una función es estrictamente creciente cuando\(a<b\) en\(I\) implica\(f(a) < f(b)\), con una definición similar sosteniendo por estrictamente decreciente.
Informalmente, una función está aumentando si como\(x\) se hace más grande (es decir, mirando de izquierda a derecha)\(f(x)\) se hace más grande.
Nuestro interés radica en encontrar intervalos\(f\) en cuyo dominio\(f\) esté aumentando o disminuyendo. Dicha información debería parecer útil. Por ejemplo, si\(f\) describe la velocidad de un objeto, es posible que queramos saber cuándo la velocidad estaba aumentando o disminuyendo (es decir, cuándo el objeto estaba acelerando vs. desacelerando). Si\(f\) se describe la población de una ciudad, deberíamos interesarnos cuando la población está creciendo o disminuyendo.
Para encontrar tales intervalos, nuevamente consideramos líneas secantes. Dejar\(f\) ser una función creciente, diferenciable en un intervalo abierto\(I\), como la que se muestra en la Figura\(\PageIndex{2}\), y dejar\(a<b\) ser dada en\(I\). Se dibuja la línea secante en la gráfica\(f\) de de\(x=a\) a\(x=b\); tiene una pendiente de\((f(b)-f(a))/(b-a)\). Pero tenga en cuenta:
\[\dfrac{f(b)-f(a)}{b-a} \Rightarrow \dfrac{\text{numerator }>0}{\text{denominator } >0} \Rightarrow \text{slope of the secent line} >0 \Rightarrow \text{Average rate of chjange of $f$ on $[a,b]$ is $>0$.} \]
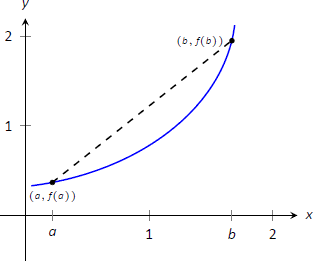
Figura\(\PageIndex{2}\): Examinando la línea secante de una función creciente.
Hemos mostrado matemáticamente lo que puede haber sido ya obvio: cuando\(f\) va en aumento, sus líneas secantes tendrán una pendiente positiva. Ahora recordemos el Teorema del Valor Medio garantiza que hay un número\(c\), donde\(a<c<b\), tal que
\[f'(c) = \frac{f(b)-f(a)}{b-a}>0.\]
Al considerar todas esas líneas secantes en\(I\), implicamos fuertemente que\(f'(x) \geq 0\) en\(I\). Se puede hacer una declaración similar para funciones decrecientes.
Nuestra lógica anterior puede resumirse como “Si\(f\) va en aumento, entonces probablemente\(f'\) sea positiva”. El teorema\(\PageIndex{1}\) a continuación le da la vuelta a esto al afirmar “Si\(f'\) es positivo, entonces\(f\) está aumentando”. Esto nos lleva a un método para encontrar cuándo las funciones están aumentando y disminuyendo.
Teorema\(\PageIndex{1}\): Test For Increasing/Decreasing Functions
Dejar\(f\) ser una función continua sobre\([a,b]\) y diferenciable en\((a,b)\).
- Si\(f'(c) > 0\) para todos\(c\) en\((a,b)\), entonces\(f\) va aumentando en\([a,b]\).
- Si\(f'(c) <0\) para todos\(c\) en\((a,b)\), entonces\(f\) está disminuyendo en\([a,b]\).
- Si\(f'(c) =0\) para todos\(c\) adentro\((a,b)\), entonces\(f\) es constante encendido\([a,b]\).
Nota: El teorema\(\PageIndex{1}\) también mantiene si\(f'(c) = 0\) para un número finito de valores de\(c\) in\(I\).
Dejar\(a\) y\(b\) estar en\(I\) donde\(f'(a)>0\) y\(f'(b)<0\). Del Teorema del Valor Intermedio se deduce que debe haber algún valor\(c\) entre\(a\) y\(b\) dónde\(f'(c) = 0\). Esto nos lleva al siguiente método para encontrar intervalos en los que una función está aumentando o disminuyendo.
Idea Clave 3: Encontrar Intervalos en los que\(f\) is Increasing or Decreasing
Dejar\(f\) ser una función diferenciable en un intervalo I. Para encontrar intervalos en los que\(f\) va en aumento y decreciente:
- Encuentra los valores críticos de\(f\). Es decir, encontrar todos\(c\) en\(I\) donde\(f'(c) = 0\) o no\(f'\) se define.
- Utilice los valores críticos para\(I\) dividirlos en subintervalos.
- Elija cualquier punto\(p\) en cada subintervalo y encuentre el signo de\(f'(p)\).
- Si\(f'(p)>0\), entonces\(f\) va aumentando en ese subintervalo.
- Si\(f'(p)<0\), entonces\(f\) está disminuyendo en ese subintervalo.
Demostramos el uso de este proceso en el siguiente ejemplo.
Ejemplo\(\PageIndex{1}\): Finding intervals of increasing/decreasing
Vamos\(f(x) = x^3+x^2-x+1\). Encuentra intervalos en los que\(f\) va aumentando o disminuyendo.
Solución
Usando la Idea Clave 3, primero encontramos los valores críticos de\(f\). Tenemos\(f'(x) = 3x^2+2x-1 = (3x-1)(x+1)\), así que\(f'(x) = 0\) cuándo\(x=-1\) y cuándo\(x=1/3\). \(f'\)nunca está indefinido.
Dado que no se especificó un intervalo para que consideremos, consideramos todo el dominio del\(f\) cual es\((-\infty,\infty)\). Así, dividimos toda la línea real en tres subintervalos basados en los dos valores críticos que acabamos de encontrar:\((-\infty,-1)\),\((-1,1/3)\) y\((1/3,\infty)\). Esto se muestra en la Figura\(\PageIndex{3}\).
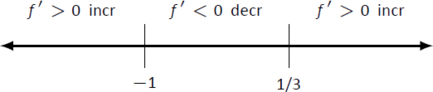
Figura\(\PageIndex{3}\): Línea numérica para\(f\) en Ejemplo\(\PageIndex{1}\)
Ahora elegimos un valor\(p\) en cada subintervalo y encontramos el signo de\(f'(p)\). Todo lo que nos importa es el signo, así que en realidad no tenemos que computar completamente\(f'(p)\); escoger valores “agradables” que lo hagan sencillo.
Subintervalo 1,\((-\infty,-1)\): Nosotros (arbitrariamente) escogemos\(p=-2\). Podemos calcular\(f'(-2)\) directamente:\(f'(-2) = 3(-2)^2+2(-2)-1=7>0\). Concluimos que\(f\) está aumentando en\((-\infty,-1)\).
Tenga en cuenta que podemos llegar a la misma conclusión sin cómputos. Por ejemplo, podríamos elegir\(p=-100\). El primer término en\(f'(-100)\), es decir,\(3(-100)^2\) es claramente positivo y muy grande. Los otros términos son pequeños en comparación, así que sabemos\(f'(-100)>0\). Todo lo que necesitamos es la señal.
Subintervalo 2,\((-1,1/3)\): Elegimos\(p=0\) ya que ese valor parece fácil de tratar. \(f'(0) = -1<0\). Concluimos que\(f\) está disminuyendo en\((-1,1/3)\).
Subintervalo 3,\((1/3,\infty)\): Elija un valor arbitrariamente grande para\(p>1/3\) y anote eso\(f'(p) =3p^2+2p-1 >0\). Concluimos que\(f\) está aumentando en\((1/3,\infty)\).
Podemos verificar nuestros cálculos considerando Figura\(\PageIndex{4}\), donde\(f\) se grafica. La gráfica también presenta\(f'\); anote cómo\(f'>0\) cuándo\(f\) está aumentando y\(f'<0\) cuándo\(f\) está disminuyendo.
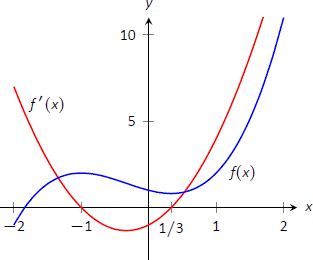
Figura\(\PageIndex{4}\): Una gráfica de\(f(x)\) en Ejemplo\(\PageIndex{1}\), que muestra dónde\(f\) está aumentando y disminuyendo.
Uno se justifica al preguntarse por qué se hace tanto trabajo cuando la gráfica parece dejar muy claros los intervalos. Damos tres razones por las que vale la pena el trabajo anterior.
En primer lugar, los puntos en\(f\) los que cambia de aumentar a disminuir no se conocen con precisión dada una gráfica. La gráfica nos muestra algo significativo que sucede cerca\(x=-1\) y\(x=0.3\), pero no podemos determinar exactamente de dónde a partir de la gráfica.
Se podría argumentar que solo encontrar valores críticos es importante; una vez que sabemos que los puntos significativos son\(x=-1\) y\(x=1/3\), el gráfico muestra los rasgos de aumento/disminución muy bien. Eso es cierto. Sin embargo, la técnica prescrita aquí ayuda a reforzar la relación entre aumentar/disminuir y el signo de\(f'\). Una vez obtenido el dominio de este concepto (y varios otros), se encuentra que o bien (a) solo se calculan los puntos críticos y la gráfica muestra todo lo demás que se desea, o (b) nunca se produce una gráfica, porque determinar el aumento/disminución usando\(f'\) es sencillo y la gráfica es innecesaria .
Entonces, nuestra segunda razón por la que vale la pena el trabajo anterior es esta: una vez que se adquiere el dominio de un tema, se tienen opciones para encontrar la información necesaria. Estamos trabajando para desarrollar el dominio.
Por último, nuestra tercera razón: muchos problemas que enfrentamos “en el mundo real” son muy complejos. Las soluciones son manejables solo mediante el uso de computadoras para hacer muchos cálculos por nosotros. Las computadoras no resuelven los problemas “por su cuenta”, sin embargo; necesitan ser enseñadas (es decir, programadas) para hacer las cosas correctas. Sería beneficioso darle una función a una computadora y que ésta devuelva valores máximos y mínimos, intervalos en los que la función está aumentando y disminuyendo, las ubicaciones de máximos relativos, etc. El trabajo que estamos haciendo aquí es fácilmente programable. Es difícil enseñar a una computadora a “mirar la gráfica y ver si va hacia arriba o hacia abajo”. Es fácil enseñar a una computadora a “determinar si un número es mayor o menor que 0”.
En la Sección 3.1 aprendimos la definición de máximos y mínimos relativos y encontramos que ocurren en puntos críticos. Ahora estamos aprendiendo que las funciones pueden cambiar de aumentar a disminuir (y viceversa) en puntos críticos. Esta nueva comprensión del aumento y la disminución crea un gran método para determinar si un punto crítico corresponde a un máximo, mínimo, o ninguno. Imagínese una función aumentando hasta un punto crítico en\(x=c\), después de lo cual disminuye. Un boceto rápido ayuda a confirmar que\(f(c)\) debe ser un máximo relativo. Se puede hacer una declaración similar para mínimos relativos. Formalizamos este concepto en un teorema.
Teorema\(\PageIndex{2}\): First Derivative Test
Dejar\(f\) ser diferenciable\(I\) y dejar\(c\) ser un número crítico en\(I\).
- Si el signo de\(f'\) cambia de positivo a negativo en\(c\), entonces\(f(c)\) es un máximo relativo de\(f\).
- Si el signo de\(f'\) cambia de negativo a positivo en\(c\), entonces\(f(c)\) es un mínimo relativo de\(f\).
- Si el signo de\(f'\) no cambia en\(c\), entonces no\(f(c)\) es un extrema relativo de\(f\).
Ejemplo\(\PageIndex{2}\): Using the First Derivative Test
Encuentre los intervalos en los que\(f\) está aumentando y disminuyendo, y use la Prueba de Primera Derivada para determinar los extremos relativos de\(f\), donde
\[f(x) = \frac{x^2+3}{x-1}.\]
Solución
Comenzamos por señalar el dominio de\(f\):\((-\infty,1)\cup(1,\infty)\). La Idea Clave 3 describe cómo encontrar intervalos donde\(f\) está aumentando y disminuyendo cuando el dominio de\(f\) es un intervalo. Dado que el dominio de\(f\) en este ejemplo es la unión de dos intervalos, aplicamos las técnicas de la Idea Clave 3 a ambos intervalos del dominio de\(f\).
Dado que no\(f\) se define en\(x=1\), la naturaleza aumento/decreciente de\(f\) podría cambiar a este valor. No consideramos formalmente que\(x=1\) sea un valor crítico de\(f\), pero lo incluiremos en nuestra lista de valores críticos que encontremos a continuación.
Usando la Regla del Cociente, encontramos
\[f'(x) = \frac{x^2-2x-3}{(x-1)^2}.\]
Necesitamos encontrar los valores críticos de\(f\); queremos saber cuándo\(f'(x)=0\) y cuándo no\(f'\) está definido. Eso último es sencillo: cuando el denominador de\(f'(x)\) es 0, no\(f'\) está definido. Eso ocurre cuando\(x=1\), que ya hemos reconocido como un valor importante.
Nota: Estrictamente hablando, no\(x=1\) es un valor crítico de\(f\) como no\(f\) se define en\(x=1\). Por lo tanto, realmente aplicamos Key Idea 3 a los intervalos\((-\infty,1)\) y\((1,\infty)\). Tomamos nota\(x=1\) en la recta numérica ya que reconocemos que el comportamiento de\(f\) puede cambiar ahí, ya que no se define ahí.
\(f'(x)=0\)cuando el numerador de\(f'(x)\) es 0. Eso ocurre cuando\(x^2-2x-3 = (x-3)(x+1) = 0\); es decir, cuando\(x=-1,3\).
Hemos encontrado que\(f\) tiene dos números críticos,\(x=-1,3\), y en\(x=1\) algo importante también podría suceder. Estos tres números dividen la línea numérica real en 4 subintervalos:
\[(-\infty,-1), \quad (-1, 1), \quad (1,3) \quad \text{and} \quad (3,\infty).\]
Elija un número\(p\) de cada subintervalo y pruebe el signo de\(f'\) at\(p\) para determinar si\(f\) está aumentando o disminuyendo en ese intervalo. Nuevamente, hacemos bien en evitar cálculos complicados; notar que el denominador de siempre\(f'\) es positivo para que podamos ignorarlo durante nuestro trabajo.
Intervalo 1,\((-\infty,-1)\): Elegir un número muy pequeño (es decir, un número negativo con una gran magnitud)\(p\) devuelve\(p^2-2p-3\) en el numerador de\(f'\); eso será positivo. De ahí\(f\) que esté aumentando en\((-\infty,-1)\).
Intervalo 2,\((-1,1)\): Elegir 0 parece simple:\(f'(0)=-3<0\). Concluimos que\(f\) está disminuyendo en\((-1,1)\).
Intervalo 3,\((1,3)\): Elegir 2 parece simple:\(f'(2) = -3<0\). Nuevamente,\(f\) está disminuyendo.
Intervalo 4,\((3,\infty)\): Elegir un número muy grande\(p\) de este subintervalo dará un numerador positivo y (por supuesto) un denominador positivo. Así\(f\) es aumentando en\((3,\infty)\).
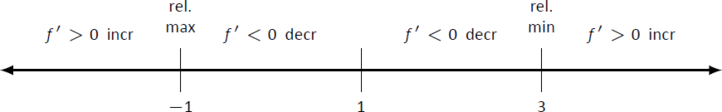
Figura\(\PageIndex{5}\): Línea numérica para\(f\) en Ejemplo\(\PageIndex{2}\)
En resumen,\(f\) va aumentando en el set\((-\infty,-1)\cup (3,\infty)\) y va disminuyendo en el set\((-1,1)\cup (1,3)\). Dado que en\(x=-1\), el signo de f'\ cambió de positivo a negativo, Teorema\(\PageIndex{2}\) afirma que\(f(-1)\) es un máximo relativo de\(f\). At\(x=3\), el signo de f'\ cambió de negativo a positivo, el significado\(f(3)\) es un mínimo relativo. At\(x=1\), no\(f\) está definido, por lo que no hay ningún extremo relativo at\(x=1\).
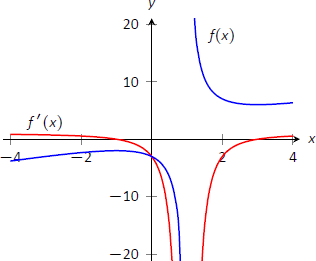
Figura\(\PageIndex{6}\): Una gráfica de\(f(x)\) en Ejemplo\(\PageIndex{2}\), que muestra dónde\(f\) está aumentando y disminuyendo.
Esto se resume en la recta numérica que se muestra en la Figura\(\PageIndex{3}\). Además, la Figura\(\PageIndex{4}\) muestra una gráfica de\(f\), confirmando nuestros cálculos. Esta cifra también muestra\(f'\), demostrando nuevamente que\(f\) está aumentando cuando\(f'>0\) y disminuyendo cuando\(f'<0\).
A menudo se ve tentado a pensar que las funciones siempre alternan “aumentar, disminuir, aumentar, disminuir\(\ldots\)”, alrededor de valores críticos. Nuestro ejemplo anterior demostró que no siempre es así. Si bien técnicamente no\(x=1\) era un valor crítico, era un valor importante que debíamos considerar. Encontramos que\(f\) fue decreciente en “ambos lados de\(x=1.\)”
Examinamos un ejemplo más.
Ejemplo\(\PageIndex{3}\): Using the First Derivative Test
Encuentra los intervalos en los que\(f(x) = x^{8/3}-4x^{2/3}\) va en aumento y decreciente e identifica los extremos relativos.
Solución
De nuevo empezamos con tomar derivados. Como sabemos que queremos resolver\(f'(x) = 0\), haremos algo de álgebra después de tomar derivados.
\[\begin{align} f(x) &= x^{\frac{8}{3}}-4x^{\frac{2}{3}} \\ f'(x) &= \dfrac{8}{3} x^{\frac{5}{3}} - \dfrac{8}{3}x^{-\frac{1}{3}} \\ &= \dfrac{8}{3}x^{-\frac{1}{3}} \left(x^{\frac{6}{3}}-1 \right)\\ &=\frac{8}{3}x^{-\frac{1}{3}}(x^2-1)\\ &=\frac{8}{3}x^{-\frac{1}{3}}(x-1)(x+1). \end{align}\]
Esta derivación de\(f'\) muestra que\(f'(x) = 0\) cuando\(x=\pm 1\) y no\(f'\) se define cuando\(x=0\). Así tenemos 3 valores críticos, dividiendo la recta numérica en 4 subintervalos como se muestra en la Figura\(\PageIndex{5}\).
Intervalo 1,\((\infty,-1)\): Elegimos\(p=-2\); podemos verificarlo fácilmente\(f'(-2)<0\). Entonces\(f\) está disminuyendo en\((-\infty,-1)\).
Intervalo 2,\((-1,0)\): Elegir\(p=-1/2\). Una vez más practicamos encontrar el signo de\(f'(p)\) sin computar un valor real. Tenemos\($f'(p) = (8/3)p^{-1/3}(p-1)(p+1)\); encuentra el signo de cada uno de los tres términos.
\[f'(p) = \frac 83 \cdot \underbrace{p^{-\frac13}}_{<0}\cdot \underbrace{(p-1)}_{<0}\underbrace{(p+1)}_{>0}.\]
Tenemos un “negativo\(\times\) negativo\(\times\) positivo” dando un número positivo;\(f\) está aumentando en\((-1,0)\).
Intervalo 3,\((0,1)\): Hacemos un análisis de signos similar al anterior, utilizando\(p\) in\((0,1)\).
\[f'(p) = \frac 83 \cdot \underbrace{p^{-\frac13}}_{>0}\cdot \underbrace{(p-1)}_{<0}\underbrace{(p+1)}_{>0}.\]
Tenemos 2 factores positivos y un factor negativo;\(f'(p)<0\) y así\(f\) es decreciente\((0,1)\).
Intervalo 4,\((1,\infty)\): Un trabajo similar al realizado para los otros tres intervalos muestra que\(f'(x)>0\) on\((1,\infty)\), por lo que\(f\) va aumentando en este intervalo.
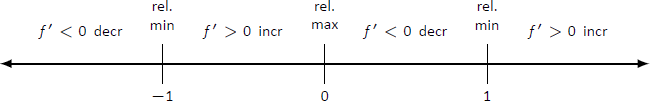
Figura\(\PageIndex{7}\): Línea numérica para\(f\) en Ejemplo\(\PageIndex{3}\)
Concluimos afirmando que\(f\) está aumentando\((-1,0) \cup (1,\infty)\) y disminuyendo en\((-\infty,-1) \cup (0,1)\). El signo de\(f'\) cambios de negativo a positivo alrededor\(x=-1\) y\(x=1\), es decir, por Teorema\(\PageIndex{2}\) que\(f(-1)\) y\(f(1)\) son mínimos relativos de\(f\). Como signo de\(f'\) cambios de positivo a negativo en\(x=0\), tenemos un máximo relativo en\(f(0)\). La figura\(\PageIndex{8}\) muestra una gráfica de\(f\), confirmando nuestro resultado. También graficamos\(f'\), resaltando una vez más que\(f\) está aumentando cuando\(f'>0\) y es decreciente cuando\(f'<0\).
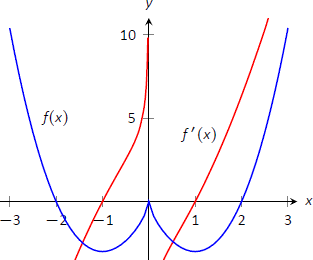
Figura\(\PageIndex{8}\): Una gráfica de\(f(x)\) en Ejemplo\(\PageIndex{3}\), que muestra dónde\(f\) está aumentando y disminuyendo.
Hemos visto cómo la primera derivada de una función ayuda a determinar cuándo la función va “arriba” o “abajo”. En la siguiente sección, veremos cómo la segunda derivada ayuda a determinar cómo se curva la gráfica de una función.


