7.6: Fuerzas Fluidas

En la lamentable situación de un automóvil que se mete en una masa de agua, la sabiduría convencional es que la presión del agua sobre las puertas rápidamente será tan grande que serán efectivamente inabribles. (Las técnicas de supervivencia sugieren abrir inmediatamente la puerta, rodar hacia abajo o romper la ventana, o esperar hasta que el agua llene el interior en cuyo punto se iguala la presión y la puerta se abrirá. Consulta el episodio #72 de Mythbusters para ver a Adam Savage probar estas opciones.) ¿Cómo puede ser esto cierto? ¿Cuánta fuerza se necesita para abrir la puerta de un auto sumergido? En esta sección encontraremos la respuesta a esta pregunta examinando las fuerzas ejercidas por los fluidos.

Comenzamos con la presión, la cual está relacionada con la fuerza por las siguientes ecuaciones:

\[\text{Pressure} = \frac{\text{Force}}{\text{Area}}\quad \Leftrightarrow \quad\text{Force} = \text{Pressure}\times\text{Area}.\]

En el contexto de los fluidos, tenemos la siguiente definición.

Definición 26: Presión de fluido

Dejar\(w\) ser el peso-densidad de un fluido. La presión\(p\) ejercida sobre un objeto a profundidad\(d\) en el fluido es\(p = w\cdot d\).

Utilizamos esta definición para encontrar la fuerza ejercida sobre una hoja horizontal considerando el área de la hoja.

Ejemplo\(\PageIndex{1}\): Computing fluid force

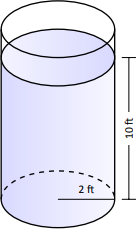
1. Un tanque de almacenamiento cilíndrico tiene un radio de 2 pies y contiene 10 pies de un fluido con una densidad de peso de 50 lb/ft\(^3\) (Figura\(\PageIndex{1}\).) ¿Cuál es la fuerza ejercida sobre la base del cilindro por el fluido?

Figura\(\PageIndex{1}\): Un tanque cilíndrico en el Ejemplo\(\PageIndex{1}\).

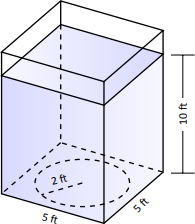
1. Un tanque rectangular cuya base es un cuadrado de 5 pies tiene una escotilla circular en la parte inferior con un radio de 2 pies. El tanque contiene 10 pies de un fluido con una densidad de peso de 50 lb/ft\(^3\). (Figura\(\PageIndex{2}\)). ¿Cuál es la fuerza ejercida sobre la escotilla por el fluido?

Figura\(\PageIndex{2}\): Un tanque rectangular en el Ejemplo\(\PageIndex{1}\).

Solución

1. Usando la Definición 26, calculamos que la presión ejercida sobre la base del cilindro es\(w\cdot d = 50 \text{ lb/ft}^3\times 10\text{ ft} = 500\) lb/ft\(^2\). El área de la base es\(\pi\cdot 2^2 = 4\pi\) ft\(^2\). Entonces la fuerza ejercida por el fluido es\[F = 500\times 4\pi = 6283\text{ lb}. \nonumber\] Tenga en cuenta que efectivamente acabamos de calcular el peso del fluido en el tanque.
2. Las dimensiones del tanque en este problema son irrelevantes. Todo lo que nos preocupa son las dimensiones de la escotilla y la profundidad del fluido. Dado que las dimensiones de la escotilla son las mismas que las de la base del tanque en la parte anterior de este ejemplo, como es la profundidad, vemos que la fuerza del fluido es la misma. Es decir,\(F = 6283\) lb.

Un concepto clave para entender aquí es que estamos midiendo efectivamente el peso de una columna de agua de 10 pies por encima de la escotilla. El tamaño del tanque que contiene el fluido no importa.

El ejemplo anterior demuestra que calcular la fuerza ejercida sobre una placa orientada horizontalmente es relativamente fácil de calcular. ¿Qué pasa con una placa orientada verticalmente? Por ejemplo, supongamos que tenemos un ojo de buey circular ubicado a un costado de un submarino. ¿Cómo calculamos la fuerza de fluido que se ejerce sobre él?

El Principio de Pascal establece que la presión ejercida por un fluido a una profundidad es igual en todas las direcciones. Por lo tanto, la presión sobre cualquier porción de una placa que esté a 1 pie por debajo de la superficie del agua es la misma sin importar cómo esté orientada la placa. (Así, un cubo hueco sumergido a gran profundidad no será simplemente “aplastado” desde arriba, sino que los lados también se arrugarán. El fluido ejercerá fuerza en todos los lados del cubo.)

Por lo tanto, considere una placa orientada verticalmente como se muestra en la Figura\(\PageIndex{3}\) sumergida en un fluido con peso-densidad\(w\). ¿Cuál es la fuerza total del fluido ejercida sobre esta placa? Encontramos esta fuerza aproximando primero la fuerza sobre pequeñas tiras horizontales.

Figura\(\PageIndex{3}\): Una placa delgada orientada verticalmente sumergida en un fluido con densidad ponderal w.

Deje que la parte superior de la placa esté a profundidad\(b\) y deje que la parte inferior esté a profundidad\(a\). (Por ahora asumimos que la superficie del fluido está a la profundidad 0, así que si el fondo de la placa está a 3 pies debajo de la superficie, tenemos\(a=-3\). Volveremos a esto más adelante.) Particionamos el intervalo\([a,b]\) en\(n\) subintervalos

\[ a = y_1 < y_2 < \cdots <y_{n+1} = b, \]

con el\(i\,^\text{th}\) subintervalo teniendo longitud\(\Delta y_i\). La fuerza\(F_i\) ejercida sobre la placa en el\(i\,^\text{th}\) subintervalo es\(F_i = \text{Pressure}\times \text{Area}.\)

La presión es profundidad\(\times w\). Aproximamos la profundidad de esta tira delgada eligiendo cualquier valor\(d_i\) en\([y_i,y_{i+1}]\); la profundidad es aproximadamente\(-d_i\). (Nuestra convención ha\(d_i\) sido un número negativo, por lo que\(-d_i\) es positivo.) Por conveniencia, dejamos\(d_i\) ser un punto final del subintervalo; dejamos\(d_i = y_i\).

El área de la tira delgada es aproximadamente de largo\(\times\) ancho. El ancho es\(\Delta y_i\). La longitud es una función de algún\(y\) -valor\(c_i\) en el\(i\,^\text{th}\) subintervalo. Nosotros declaramos que la longitud es\(\ell(c_i)\). Así

\ [\ begin {align*}
f_i &=\ texto {Presión}\ veces\ texto {Área}\\
&= -y_i\ cdot w\ veces\ ell (c_i)\ cdot\ Delta y_i.
\ end {align*}\]

Para aproximar la fuerza total, sumamos las fuerzas aproximadas en cada una de las tiras\(n\) delgadas:

\[F = \sum_{i=1}^n F_i \approx \sum_{i=1}^n -w\cdot y_i\cdot\ell(c_i)\cdot\Delta y_i.\]

Esto es, por supuesto, otro Riemann Sum. Podemos encontrar la fuerza exacta tomando un límite ya que las longitudes del subintervalo van a 0; evaluamos este límite con una integral definida.

idea clave 30: fuerza de fluido sobre una placa orientada verticalmente

Deje que una placa orientada verticalmente se sumerja en un fluido con densidad de peso\(w\) donde se encuentre la parte superior de la placa\(y=b\) y la parte inferior esté en\(y=a\). Dejar\(\ell(y)\) ser la longitud de la placa en\(y\).

1. Si\(y=0\) corresponde a la superficie del fluido, entonces la fuerza ejercida sobre la placa por el fluido es\[F=\int_a^b w\cdot(-y)\cdot\ell(y) dy.\]
2. En general, vamos a\(d(y)\) representar la distancia entre la superficie del fluido y la placa en\(y\). Entonces la fuerza ejercida sobre la placa por el fluido es

\[F=\int_a^b w\cdot d(y)\cdot\ell(y)\ dy.\]

Ejemplo\(\PageIndex{2}\): Finding fluid force

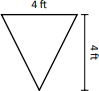
Considera una placa delgada en forma de triángulo isósceles como se muestra en la Figura\(\PageIndex{4}\) sumergida en agua con una densidad de peso de 62.4 lb/ft\(^3\). Si el fondo de la placa está a 10 pies por debajo de la superficie del agua, ¿cuál es la fuerza total de fluido ejercida sobre esta placa?

Figura\(\PageIndex{4}\): Una placa delgada en forma de triángulo isósceles en el Ejemplo 7.6.2.

Solución

Abordamos este problema de dos maneras diferentes para ilustrar las diferentes formas en que se puede implementar la Idea Clave 30. Primero dejaremos\(y=0\) representar la superficie del agua, luego consideraremos una convención alterna.

Figura\(\PageIndex{5}\): Dibujando la placa triangular en el Ejemplo 7.6.2 con la convención de que el nivel del agua está en y=0.

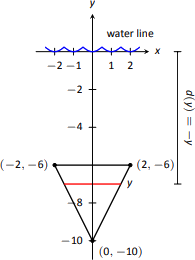
1. Dejamos\(y=0\) representar la superficie del agua; por lo tanto, el fondo de la placa está en\(y=-10\). Centramos el triángulo en el\(y\) eje -como se muestra en la Figura\(\PageIndex{5}\). La profundidad de la placa en\(y\) es la\(-y\) indicada por la Idea Clave. Consideramos ahora la longitud de la placa en\(y\).
   
   Necesitamos encontrar ecuaciones de los bordes izquierdo y derecho de la placa. El lado derecho es una línea que conecta los puntos\((0,-10)\) y\((2,-6)\): esa línea tiene ecuación\(x=1/2(y+10)\). (Encuentra la ecuación en el\(y=mx+b\) formato familiar y resuelve para\(x\).) De igual manera, el lado izquierdo se describe por la línea\(x=-1/2(y+10)\). La longitud total es la distancia entre estas dos líneas:\(\ell(y)=1/2(y+10) - (-1/2(y+10)) = y+10.\)
   
   La fuerza total del fluido es entonces\[\begin{align*}F &= \int_{-10}^{-6} 62.4(-y)(y+10) dy \\ &= 62.4\cdot \frac{176}{3} \approx 3660.8\text{ lb}.\end{align*}\]
2. A veces parece más fácil orientar la placa delgada más cerca del origen. Por ejemplo, considere la convención en la que se encuentra la parte inferior de la placa triangular\((0,0)\), como se muestra en la Figura\(\PageIndex{6}\). Las ecuaciones de los lados izquierdo y derecho son fáciles de encontrar. Son\(y=2x\) y\(y=-2x\), respectivamente, que reescribimos como\(x= 1/2y\) y\(x=-1/2y\). Así la función length es\(\ell(y) = 1/2y-(-1/2y) = y\).
   
   Como la superficie del agua está a 10 pies por encima de la base de la placa, tenemos que la superficie del agua está en\(y=10\). Así, la función de profundidad es la distancia entre\(y=10\) y\(y\);\(d(y) = 10-y\). Calculamos la fuerza total del fluido como:\[\begin{align*}F &=\int_0^4 62.4(10-y)(y)\ dy \\ &\approx 3660.8\text{ lb}.\end{align*}\]

Figura\(\PageIndex{6}\): Dibujando la placa triangular en el Ejemplo 7.6.2 con la convención de que la base del triángulo está en\((0,0)\).

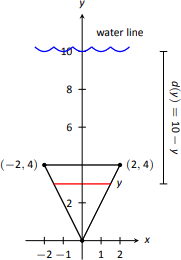
La respuesta correcta es, por supuesto, independiente de la colocación de la placa en el plano de coordenadas siempre y cuando seamos consistentes.

Ejemplo\(\PageIndex{3}\): Finding fluid force

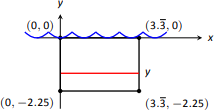
Encuentra la fuerza total de fluido en una puerta de automóvil sumergida hasta la parte inferior de su ventana en el agua, donde la puerta del automóvil es un rectángulo de 40" de largo y 27" de alto (basado en las dimensiones de un Fiat Grande Punto 2005).

Solución

La puerta del carro, como un rectángulo, se dibuja en la Figura\(\PageIndex{7}\). Su longitud es\(10/3\) ft y su altura es 2.25 ft. Adoptamos la convención de que la parte superior de la puerta está en la superficie del agua, ambas de las cuales están en\(y=0\). Usando la densidad de peso del agua de 62.4 lb/ft\(^3\), tenemos la fuerza total como

\ [\ begin {align*}
F &=\ int_ {-2.25} ^0 62.4 (-y) 10/3 dy\\
&=\ int_ {-2.25} ^0 -208y dy\\
&= -104y^2\ Big|_ {-2.25} ^0\\
&= 526.5\ text {lb.}
\ end {alinear*}\]

A la mayoría de los adultos les resultaría muy difícil aplicar más de 500 lb de fuerza a la puerta de un automóvil mientras están sentados dentro, lo que hace que la puerta sea efectivamente imposible de abrir. Esto es contrario a la intuición ya que la mayoría asume que la puerta sería relativamente fácil de abrir. Lo cierto es que no lo es, de ahí los consejos de supervivencia mencionados al inicio de esta sección.

Figura\(\PageIndex{7}\): Esbozo de una puerta de automóvil sumergida en el Ejemplo 7.6.2.

Ejemplo\(\PageIndex{4}\): Finding fluid force

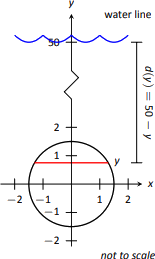
Se está construyendo una torre de observación submarina con ojos de buey circulares que permiten a los visitantes ver la vida submarina. Cada ojo de buey orientado verticalmente debe tener un diámetro de 3 pies cuyo centro se ubicará 50 pies bajo el agua. Encuentra la fuerza total del fluido ejercida sobre cada ojo de buey. Además, calcule la fuerza del fluido en un ojo de buey orientado horizontalmente que está por debajo de 50 pies de agua.

Figura\(\PageIndex{8}\): Medición de la fuerza del fluido en un ojo de buey subacuático en el Ejemplo 7.6.4.

Solución

Colocamos el centro del ojo de buey en el origen, es decir, la superficie del agua está en\(y=50\) y la función de profundidad será\(d(y)=50-y\); ver Figura\(\PageIndex{8}\).

La ecuación de un círculo con un radio de 1.5 es\(x^2+y^2=2.25\); resolviendo para\(x\) tenemos\(x=\pm \sqrt{2.25-y^2}\), donde la raíz cuadrada positiva corresponde al lado derecho del círculo y la raíz cuadrada negativa corresponde al lado izquierdo del círculo. Así la función de longitud a profundidad\(y\) es\(\ell(y) = 2\sqrt{2.25-y^2}\). Integrando en\([-1.5,1.5]\) contamos con:

\ [\ begin {alinear*}
F &= 62.4\ int_ {-1.5} ^ {1.5} 2 (50-y)\ sqrt {2.25-y^2} dy\\
&= 62.4\ int_ {-1.5} ^ {1.5}\ big (100\ sqrt {2.25-y^2} - 2y\ sqrt {2.25-y^2}\ big) dy\\
&= 6240\ int_ {-1.5} ^ {1.5}\ grande (\ sqrt {2.25-y^2}\ grande) dy - 62.4\ int_ {-1.5} ^ {1.5}\ grande (2y\ sqrt {2.25-y^2}\ grande ) dy. \\
\ final {alinear*}\]

La segunda integral anterior puede evaluarse mediante Sustitución. Déjalo\(u=2.25-y^2\) con\(du = -2y\,dy\). Los nuevos límites son:\(u(-1.5)=0\) y\(u(1.5)=0\); la nueva integral se integrará de\(u=0\) a\(u=0\), de ahí que la integral sea 0.

La primera integral anterior encuentra el área de medio círculo de radio 1.5, así la primera integral evalúa a\(6240\cdot\pi\cdot1.5^2/2 = 22,054\). Por lo tanto, la fuerza total del fluido en un ojo de buey orientado verticalmente es\(22,054\) lb.

Encontrar la fuerza en un ojo de buey orientado horizontalmente es más sencillo: $$F =\ text {Presión}\ times\ text {Área} = 62.4\ cdot50\ times\ pi\ cdot1.5^2 = 22,054\ text {lb} .$$ Que estas dos fuerzas sean iguales no es coincidencia; resulta que la fuerza de fluido aplicada a un círculo orientado verticalmente cuyo centro está en profundidad\(d\) es lo mismo que la fuerza aplicada a un círculo orientado horizontalmente en profundidad\(d\).

Terminamos este capítulo con un recordatorio de las verdaderas habilidades que se pretende desarrollar aquí. No estamos realmente preocupados por la capacidad de encontrar fuerzas fluidas o los volúmenes de sólidos de la revolución. El trabajo realizado por una fuerza variable es importante, aunque probablemente no lo sea medir el trabajo realizado al tirar de una cuerda por un acantilado.

Lo que realmente nos preocupa es la capacidad de resolver ciertos problemas aproximando primero la solución, luego refinando la aproximación, luego reconociendo si/cuándo este proceso de refinación da como resultado una integral definida a través de un límite. Conocer las fórmulas que se encuentran dentro de las cajas especiales dentro de este capítulo es beneficioso ya que ayuda a resolver los problemas que se encuentran en los ejercicios, y otras habilidades matemáticas se fortalecen aplicando adecuadamente estas fórmulas. Sin embargo, lo que es más importante, entender cómo se construyó cada una de estas fórmulas. Cada uno es el resultado de una suma de aproximaciones; cada suma era una suma de Riemann, lo que nos permitió tomar un límite y encontrar la respuesta exacta a través de una integral definida.

El siguiente capítulo aborda un tema completamente diferente: secuencias y series. En definitiva, una secuencia es una lista de números, donde una serie es la suma de una lista de números. Estas ideas aparentemente simples conducen a matemáticas muy poderosas.

Colaboradores y Atribuciones

• Template:ContribApexCalc