6.3: Volúmenes de revolución - Carcasas cilíndricas
- Page ID
- 116164
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calcular el volumen de un sólido de revolución utilizando el método de conchas cilíndricas.
- Comparar los diferentes métodos para calcular un volumen de revolución.
En esta sección, examinamos el método de las conchas cilíndricas, el método final para encontrar el volumen de un sólido de revolución. Podemos usar este método en los mismos tipos de sólidos que el método de disco o el método de arandela; sin embargo, con los métodos de disco y arandela, nos integramos a lo largo del eje de coordenadas paralelo al eje de revolución. Con el método de conchas cilíndricas, nos integramos a lo largo del eje de coordenadas perpendicular al eje de revolución. La capacidad de elegir qué variable de integración queremos utilizar puede ser una ventaja significativa con funciones más complicadas. Además, la geometría específica del sólido a veces hace que el método de usar carcasas cilíndricas sea más atractivo que usar el método de arandela. En la última parte de esta sección, revisamos todos los métodos para encontrar el volumen que hemos estudiado y establecemos algunas pautas para ayudarte a determinar qué método usar en una situación determinada.
El método de las conchas cilíndricas
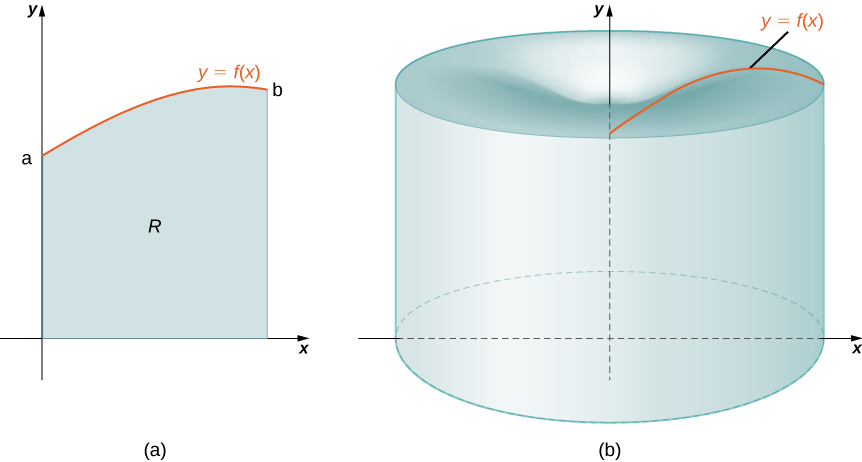
Nuevamente, estamos trabajando con un sólido de revolución. Como antes, definimos una región\(R\), delimitada arriba por la gráfica de una función\(y=f(x)\), abajo por el \(x\)eje -y a la izquierda y a la derecha por las líneas\(x=a\) y\(x=b\), respectivamente, como se muestra en la Figura\(\PageIndex{1a}\). Luego giramos esta región alrededor del\(y\) eje -como se muestra en la Figura\(\PageIndex{1b}\). Tenga en cuenta que esto es diferente a lo que hemos hecho antes. Anteriormente, las regiones definidas en términos de funciones de\(x\) giraban alrededor del \(x\)eje -o una línea paralela al mismo.
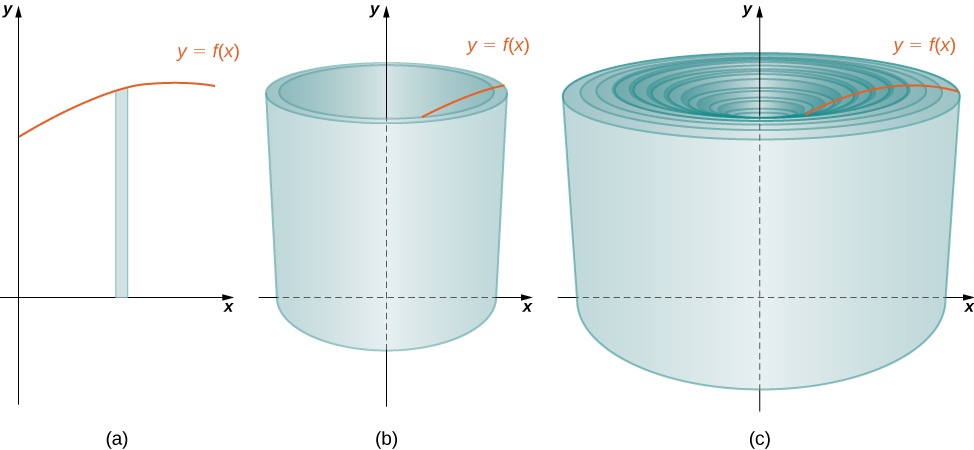
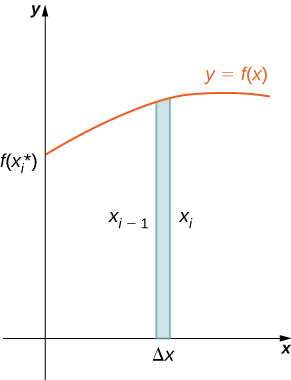
Como hemos hecho muchas veces antes, particionar el intervalo\([a,b]\) usando una partición regular,\(P={x_0,x_1,…,x_n}\) y, para\(i=1,2,…,n\), elegir un punto\(x^∗_i∈[x_{i−1},x_i]\). Luego, construya un rectángulo sobre el intervalo\([x_{i−1},x_i]\) de altura\(f(x^∗_i)\) y ancho\(Δx\). En la Figura se muestra un rectángulo representativo\(\PageIndex{2a}\). Cuando ese rectángulo gira alrededor del\(y\) eje -eje, en lugar de un disco o una arandela, obtenemos una cáscara cilíndrica, como se muestra en la Figura\(\PageIndex{2}\).
Para calcular el volumen de esta concha, considere Figura\(\PageIndex{3}\).
El caparazón es un cilindro, por lo que su volumen es el área de la sección transversal multiplicada por la altura del cilindro. Las secciones transversales son anillos (regiones en forma de anillo, esencialmente, círculos con un agujero en el centro), con radio exterior\(x_i\) y radio interior\(x_{i−1}\). Así, el área de la sección transversal es\(πx^2_i−πx^2_{i−1}\). La altura del cilindro es\(f(x^∗_i).\) Entonces el volumen de la carcasa es
\[ \begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_{i}−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}). \end{align*}\]
Tenga en cuenta que\(x_i−x_{i−1}=Δx,\) así tenemos
\[V_{shell}=2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)\,Δx. \nonumber \]
Además,\(\dfrac {x_i+x_{i−1}}{2}\) es tanto el punto medio del intervalo\([x_{i−1},x_i]\) como el radio promedio de la concha, y podemos aproximarlo por\(x^∗_i\). Entonces tenemos
\[V_{shell}≈2π\,f(x^∗_i)x^∗_i\,Δx. \nonumber \]
Otra forma de pensar en esto es pensar en hacer un corte vertical en el caparazón y luego abrirlo para formar una placa plana (Figura\(\PageIndex{4}\)).
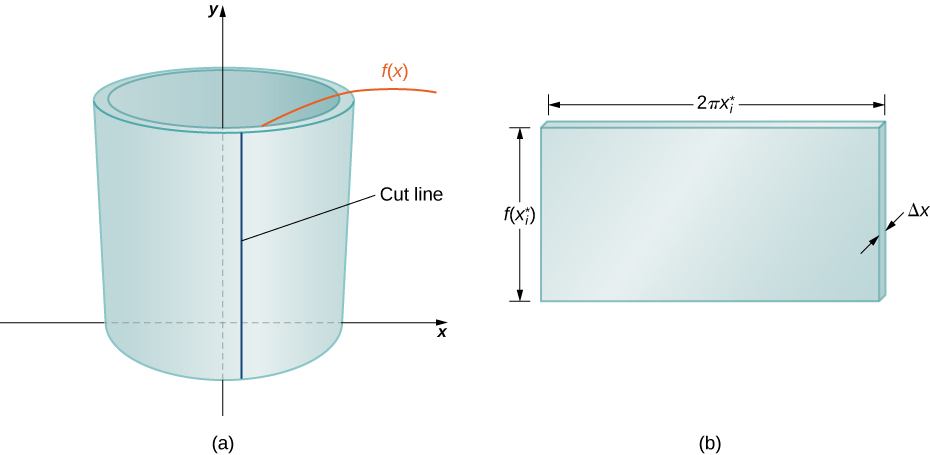
En realidad, el radio exterior de la carcasa es mayor que el radio interno, y por lo tanto el borde posterior de la placa sería ligeramente más largo que el borde frontal de la placa. Sin embargo, podemos aproximar el caparazón aplanado mediante una placa plana de altura\(f(x^∗_i)\)\(2πx^∗_i\), ancho y grosor\(Δx\) (Figura). El volumen de la concha, entonces, es aproximadamente el volumen de la placa plana. Multiplicando la altura, ancho y profundidad de la placa, obtenemos
\[V_{shell}≈f(x^∗_i)(2π\,x^∗_i)\,Δx, \nonumber \]
que es la misma fórmula que teníamos antes.
Para calcular el volumen de todo el sólido, luego agregamos los volúmenes de todas las conchas y obtenemos
\[V≈\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx). \nonumber \]
Aquí tenemos otra suma de Riemann, esta vez para la función\(2π\,x\,f(x).\) Tomando el límite como nos\(n→∞\) da
\[V=\lim_{n→∞}\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx)=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]
Esto lleva a la siguiente regla para el método de las conchas cilíndricas.
Dejar\(f(x)\) ser continuo y no negativo. Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)\), abajo por el \(x\)eje -, a la izquierda por la línea\(x=a\), y a la derecha por la línea\(x=b\). Entonces el volumen del sólido de revolución formado al girar\(R\) alrededor del\(y\) eje viene dado por
\[V=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]
Ahora consideremos un ejemplo.
Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)=1/x\) y abajo por el \(x\)eje -sobre el intervalo\([1,3]\). Encuentra el volumen del sólido de revolución formado al girar\(R\) alrededor del\(y\) eje.
Solución
Primero debemos graficar la región\(R\) y el sólido asociado de revolución, como se muestra en la Figura\(\PageIndex{5}\).
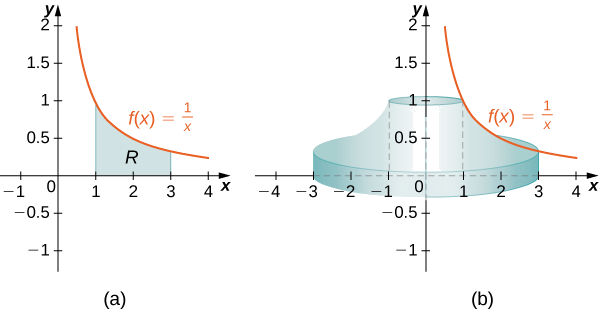
Figura\(\PageIndex{5}\) (c) Visualizando el sólido de revolución con CalcPlot3D.
Entonces el volumen del sólido viene dado por
\[ \begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^3_1\left(2π\,x\left(\dfrac {1}{x}\right)\right)\,dx \\ =\int ^3_12π\,dx\\ =2π\,x\bigg|^3_1=4π\,\text{units}^3. \end{align*}\]
Defina R como la región delimitada arriba por la gráfica de\(f(x)=x^2\) y por debajo por el\(x\) eje -sobre el intervalo\([1,2]\). Encuentra el volumen del sólido de revolución formado al girar\(R\) alrededor del\(y\) eje.
- Pista
-
Utilice el procedimiento de Ejemplo\(\PageIndex{1}\).
- Contestar
-
\(\dfrac{15π}{2} \, \text{units}^3 \)
Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)=2x−x^2\) y abajo por el\(x\) eje -sobre el intervalo\([0,2]\). Encuentra el volumen del sólido de revolución formado al girar\(R\) alrededor del \(y\)eje.
Solución
Primero grafica la región\(R\) y el sólido asociado de revolución, como se muestra en la Figura\(\PageIndex{6}\).
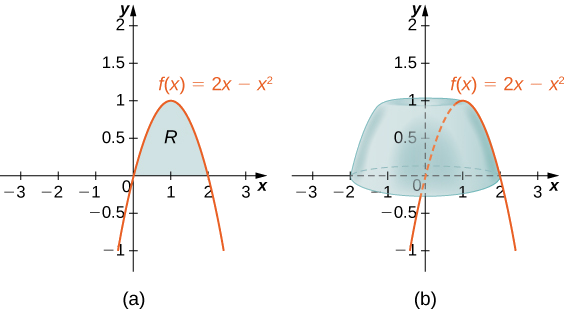
Entonces el volumen del sólido viene dado por
\[\begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^2_0(2π\,x(2x−x^2))\,dx \\ = 2π\int ^2_0(2x^2−x^3)\,dx \\ =2π \left. \left[\dfrac {2x^3}{3}−\dfrac {x^4}{4}\right]\right|^2_0 \\ =\dfrac {8π}{3}\,\text{units}^3 \end{align*}\]
Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)=3x−x^2\) y abajo por el\(x\) eje -sobre el intervalo\([0,2]\). Encuentra el volumen del sólido de revolución formado al girar\(R\) alrededor del\(y\) eje.
- Pista
-
Utilice el proceso de Ejemplo\(\PageIndex{2}\).
- Contestar
-
\(8π \, \text{units}^3 \)
Al igual que con el método de disco y el método de arandela, podemos utilizar el método de conchas cilíndricas con sólidos de revolución, girados alrededor del\(x\) eje -eje, cuando queremos integrar con respecto a\(y\). Aquí se da la regla análoga para este tipo de sólidos.
Dejar\(g(y)\) ser continuo y no negativo. Definir\(Q\) como la región delimitada a la derecha por la gráfica de\(g(y)\), a la izquierda por el\(y\) eje -eje, abajo por la línea\(y=c\), y arriba por la línea\(y=d\). Entonces, el volumen del sólido de revolución formado al girar\(Q\) alrededor del\(x\) eje viene dado por
\[V=\int ^d_c(2π\,y\,g(y))\,dy. \nonumber \]
Definir\(Q\) como la región delimitada a la derecha por la gráfica de\(g(y)=2\sqrt{y}\) y a la izquierda por el\(y\) eje -para\(y∈[0,4]\). Encuentra el volumen del sólido de revolución formado al girar\(Q\) alrededor del\(x\) eje.
Solución
Primero, necesitamos graficar la región\(Q\) y el sólido asociado de revolución, como se muestra en la Figura\(\PageIndex{7}\).
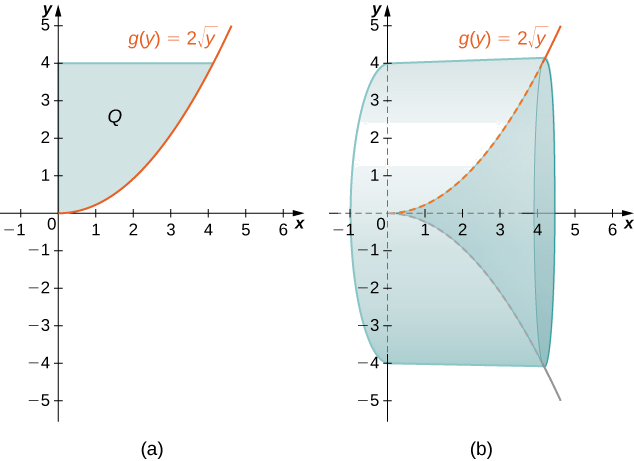
Etiquete la región sombreada\(Q\). Entonces el volumen del sólido viene dado por
\[ \begin{align*} V =\int ^d_c(2π\,y\,g(y))\,dy \\ =\int ^4_0(2π\,y(2\sqrt{y}))\,dy \\ =4π\int ^4_0y^{3/2}\,dy \\ =4π\left[\dfrac {2y^{5/2}}{5}\right]∣^4_0 \\ =\dfrac {256π}{5}\, \text{units}^3 \end{align*}\]
Definir\(Q\) como la región delimitada a la derecha por la gráfica de\(g(y)=3/y\) y a la izquierda por el\(y\) eje -para\(y∈[1,3]\). Encuentra el volumen del sólido de revolución formado al girar\(Q\) alrededor del\(x\) eje.
- Pista
-
Utilice el proceso de Ejemplo\(\PageIndex{3}\).
- Contestar
-
\(12π\)unidades 3
Para el siguiente ejemplo, observamos un sólido de revolución para el cual la gráfica de una función gira alrededor de una línea distinta de uno de los dos ejes de coordenadas. Para configurar esto, necesitamos revisar el desarrollo del método de conchas cilíndricas. Recordemos que encontramos el volumen de una de las conchas para ser dado por
\[\begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_i−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}).\end{align*}\]
Esto se basó en un proyectil con un radio exterior de\(x_i\) y un radio interno de\(x_{i−1}\). Sin embargo, si giramos la región alrededor de una línea que no sea el\(y\) eje -eje, tenemos un radio exterior e interior diferente. Supongamos, por ejemplo, que giramos la región alrededor de la línea\(x=−k,\) donde\(k\) hay alguna constante positiva. Entonces, el radio exterior del proyectil es\(x_i+k\) y el radio interior del proyectil es\(x_{i−1}+k\). Sustituyendo estos términos en la expresión para volumen, vemos que cuando una región plana se gira alrededor de la línea,\(x=−k,\) el volumen de un shell viene dado por
\[\begin{align*} V_{shell} =2π\,f(x^∗_i)(\dfrac {(x_i+k)+(x_{i−1}+k)}{2})((x_i+k)−(x_{i−1}+k)) \\[4pt] =2π\,f(x^∗_i)\left(\left(\dfrac {x_i+x_{i−2}}{2}\right)+k\right)Δx.\end{align*}\]
Como antes, notamos que\(\dfrac {x_i+x_{i−1}}{2}\) es el punto medio del intervalo\([x_{i−1},x_i]\) y se puede aproximar por\(x^∗_i\). Entonces, el volumen aproximado de la concha es
\[V_{shell}≈2π(x^∗_i+k)f(x^∗_i)Δx. \nonumber \]
El resto del desarrollo procede como antes, y vemos que
\[V=\int ^b_a(2π(x+k)f(x))dx. \nonumber \]
También podríamos rotar la región alrededor de otras líneas horizontales o verticales, como una línea vertical en el medio plano derecho. En cada caso, la fórmula de volumen debe ajustarse en consecuencia. Específicamente, el\(x\) término -en la integral debe ser reemplazado por una expresión que represente el radio de un caparazón. Para ver cómo funciona esto, considere el siguiente ejemplo.
Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)=x\) y abajo por el\(x\) eje -sobre el intervalo\([1,2]\). Encuentra el volumen del sólido de la revolución formado al girar\(R\) alrededor de la línea\(x=−1.\)
Solución
Primero, grafica la región\(R\) y el sólido asociado de revolución, como se muestra en la Figura\(\PageIndex{8}\).
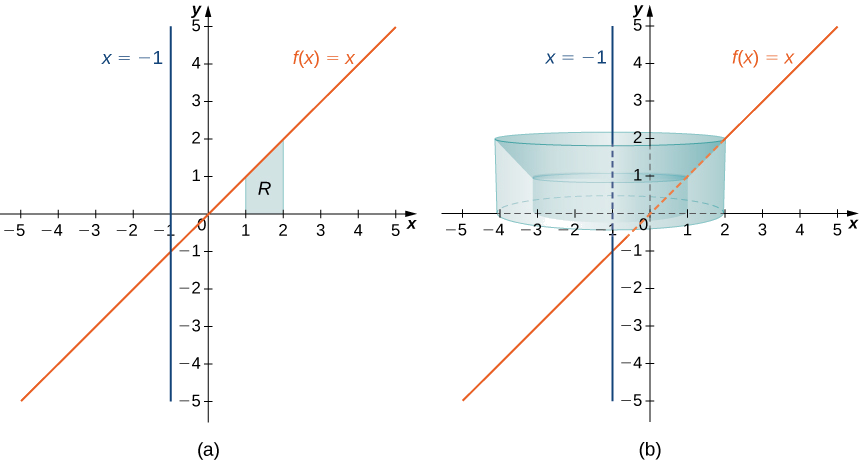
Tenga en cuenta que el radio de un proyectil viene dado por\(x+1\). Entonces el volumen del sólido viene dado por
\[\begin{align*} V =\int ^2_1 2π(x+1)f(x)\, dx \\ =\int ^2_1 2π(x+1)x \, dx=2π\int ^2_1 x^2+x \, dx \\ =2π \left[\dfrac{x^3}{3}+\dfrac{x^2}{2}\right]\bigg|^2_1 \\ =\dfrac{23π}{3} \, \text{units}^3 \end{align*}\]
Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)=x^2\) y abajo por el\(x\) eje -sobre el intervalo\([0,1]\). Encuentra el volumen del sólido de la revolución formado al girar\(R\) alrededor de la línea\(x=−2\).
- Pista
-
Utilice el proceso de Ejemplo\(\PageIndex{4}\).
- Contestar
-
\(\dfrac {11π}{6}\)unidades 3
Para nuestro último ejemplo en esta sección, veamos el volumen de un sólido de revolución para el que la región de la revolución está delimitada por las gráficas de dos funciones.
Definir\(R\) como la región delimitada arriba por la gráfica de la función\(f(x)=\sqrt{x}\) y abajo por la gráfica de la función\(g(x)=1/x\) sobre el intervalo\([1,4]\). Encuentra el volumen del sólido de revolución generado al girar\(R\) alrededor del\(y\) eje.
Solución
Primero, grafica la región\(R\) y el sólido asociado de revolución, como se muestra en la Figura\(\PageIndex{9}\).
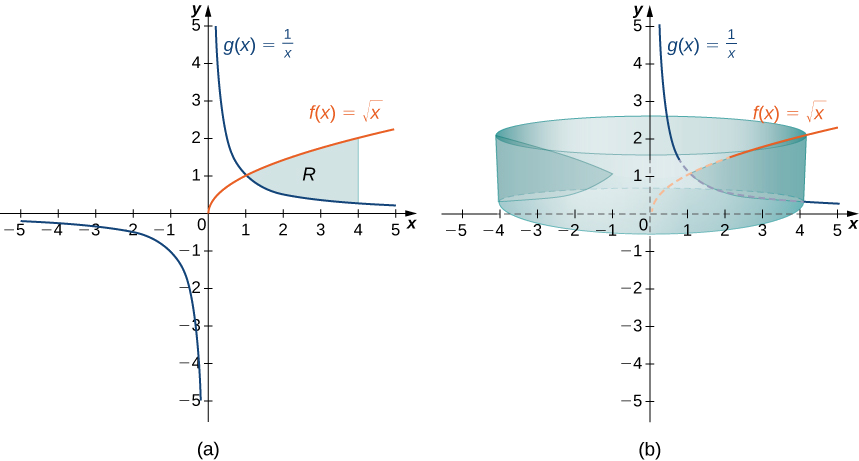
Tenga en cuenta que el eje de revolución es el\(y\) eje -eje, por lo que el radio de un caparazón viene dado simplemente por\(x\). No necesitamos hacer ningún ajuste al x-term de nuestro integrando. La altura de un caparazón, sin embargo, viene dada por\(f(x)−g(x)\), por lo que en este caso necesitamos ajustar el\(f(x)\) término del integrando. Entonces el volumen del sólido viene dado por
\[\begin{align*} V =\int ^4_1(2π\,x(f(x)−g(x)))\,dx \\[4pt] = \int ^4_1(2π\,x(\sqrt{x}−\dfrac {1}{x}))\,dx=2π\int ^4_1(x^{3/2}−1)dx \\[4pt] = 2π\left[\dfrac {2x^{5/2}}{5}−x\right]\bigg|^4_1=\dfrac {94π}{5} \, \text{units}^3. \end{align*}\]
Definir\(R\) como la región delimitada arriba por la gráfica de\(f(x)=x\) y abajo por la gráfica de\(g(x)=x^2\) sobre el intervalo\([0,1]\). Encuentra el volumen del sólido de revolución formado al girar\(R\) alrededor del\(y\) eje.
- Pista
-
Pista: Utilice el proceso de Ejemplo\(\PageIndex{5}\).
- Contestar
-
\(\dfrac {π}{6}\)unidades 3
¿Qué método debemos usar?
Hemos estudiado varios métodos para encontrar el volumen de un sólido de revolución, pero ¿cómo sabemos qué método usar? A menudo se reduce a una elección de qué integral es más fácil de evaluar. La figura\(\PageIndex{10}\) describe los diferentes enfoques para sólidos de revolución alrededor del\(x\) eje. Depende de usted desarrollar la tabla análoga para sólidos de revolución alrededor del\(y\) eje.
![Esta figura es una tabla comparando los diferentes métodos para encontrar volúmenes de sólidos de revolución. Las columnas de la tabla están etiquetadas como “comparación”, “método de disco”, “método de arandela” y “método shell”. Las filas están etiquetadas como “fórmula de volumen”, “sólido”, “intervalo a partición”, “rectángulos”, “región típica” y “rectángulo”. En la columna de método de disco, la fórmula se da como la integral definida de a a b de pi veces [f (x)] ^2. El sólido no tiene cavidad en el centro, la partición es [a, b], los rectángulos son verticales, y la región típica es una región sombreada por encima del eje x y por debajo de la curva de f (x). En la columna del método de lavado, la fórmula se da como la integral definida de a a b de pi veces [f (x)] ^2- [g (x)] ^2. El sólido tiene una cavidad en el centro, la partición es [a, b], los rectángulos son verticales, y la región típica es una región sombreada por encima de la curva de g (x) y por debajo de la curva de f (x). En la columna del método shell, la fórmula se da como la integral definida de c a d de 2pi por yg (y). El sólido está con o sin cavidad en el centro, la partición es [c, d] los rectángulos son horizontales, y la región típica es una región sombreada por encima del eje x y por debajo de la curva de g (y).](https://math.libretexts.org/@api/deki/files/2735/CNX_Calc_Figure_06_03_009.jpeg)
Echemos un vistazo a un par de problemas adicionales y decidamos cuál es el mejor enfoque a tomar para resolverlos.
Para cada uno de los siguientes problemas, seleccione el mejor método para encontrar el volumen de un sólido de revolución generado al girar la región dada alrededor del\(x\) eje -eje, y configurar la integral para encontrar el volumen (no evaluar la integral).
- La región delimitada por las gráficas de\(y=x, y=2−x,\) y el\(x\) eje.
- La región delimitada por las gráficas de\(y=4x−x^2\) y el\(x\) eje.
Solución
a.
Primero, esbozar la región y el sólido de la revolución como se muestra.
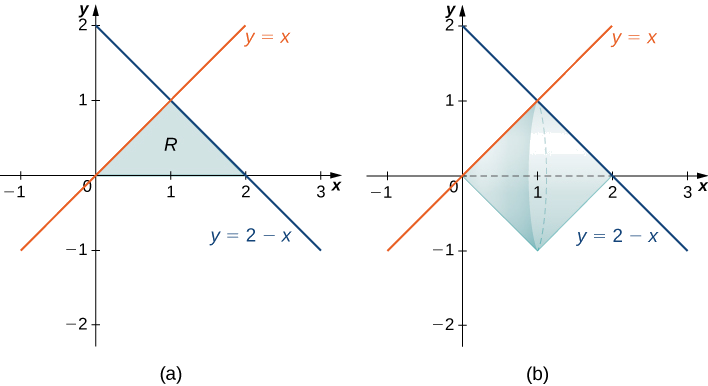
Mirando la región, si queremos integrarnos con respecto a\(x\), tendríamos que romper la integral en dos piezas, porque tenemos diferentes funciones delimitando la región sobre\([0,1]\) y\([1,2]\). En este caso, usando el método disk, tendríamos
\[V=\int ^1_0 π\,x^2\,dx+\int ^2_1 π(2−x)^2\,dx. \nonumber \]
Si en su lugar usáramos el método shell, usaríamos funciones de y para representar las curvas, produciendo
\[V=\int ^1_0 2π\,y[(2−y)−y] \,dy=\int ^1_0 2π\,y[2−2y]\,dy. \nonumber \]
Ninguna de estas integrales es particularmente onerosa, pero como el método shell requiere solo una integral, y el integrando requiere menos simplificación, probablemente deberíamos ir con el método shell en este caso.
b.
Primero, esbozar la región y el sólido de la revolución como se muestra.
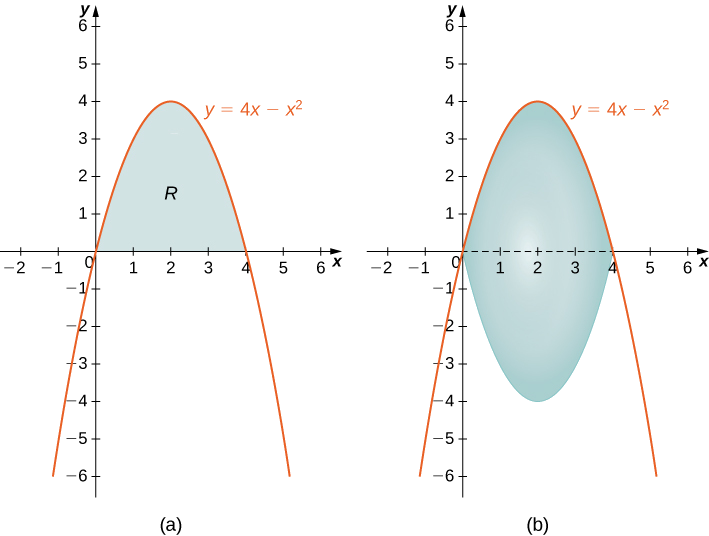
Mirando la región, sería problemático definir un rectángulo horizontal; la región está delimitada a izquierda y derecha por la misma función. Por lo tanto, podemos descartar el método de los proyectiles. El sólido no tiene cavidad en el medio, por lo que podemos usar el método de discos. Entonces
\[V=\int ^4_0π\left(4x−x^2\right)^2\,dx \nonumber \]
Seleccione el mejor método para encontrar el volumen de un sólido de revolución generado al girar la región dada alrededor del\(x\) eje, y configurar la integral para encontrar el volumen (no evaluar la integral): la región delimitada por las gráficas de\(y=2−x^2\) y\(y=x^2\).
- Pista
-
Dibuje la región y use Figura\(\PageIndex{12}\) para decidir qué integral es más fácil de evaluar.
- Contestar
-
Utilice el método de arandelas;\[V=\int ^1_{−1}π\left[\left(2−x^2\right)^2−\left(x^2\right)^2\right]\,dx \nonumber \]
Conceptos clave
- El método de conchas cilíndricas es otro método para usar una integral definida para calcular el volumen de un sólido de revolución. Este método a veces es preferible ya sea al método de discos o al método de arandelas porque integramos con respecto a la otra variable. En algunos casos, una integral es sustancialmente más complicada que la otra.
- La geometría de las funciones y la dificultad de la integración son los principales factores para decidir qué método de integración utilizar.
Ecuaciones Clave
- Método de conchas cilíndricas
\(\displaystyle V=\int ^b_a\left(2π\,x\,f(x)\right)\,dx\)
Glosario
- método de conchas cilíndricas
- un método para calcular el volumen de un sólido de revolución dividiendo el sólido en conchas cilíndricas anidadas; este método es diferente de los métodos de discos o arandelas en que integramos con respecto a la variable opuesta