9.1E: Ejercicios para la Sección 9.1

Última actualización
Guardar como PDF

Page ID: 116625

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

En los ejercicios 1 - 4, encuentra los primeros seis términos de cada secuencia, empezando por$ n=1$.

1)$a_n=1+(−1)^n$ para$ n≥1$

Contestar: $ a_n=0$si$ n$ es impar y$ a_n=2$ si$ n$ es par

2)$ a_n=n^2−1$ para$ n≥1$

3)$ a_1=1$ y$ a_n=a_{n−1}+n$ para$ n≥2$

Contestar: $ {a_n}={1,3,6,10,15,21,…}$

4)$ a_1=1, a_2=1$ y$ a_n+2=a_n+a_{n+1}$ para$ n≥1$

5) Encontrar una fórmula explícita para$ a_n$ dónde$ a_1=1$ y$ a_n=a_{n−1}+n$ para$ n≥2$.

Contestar: $ a_n=\dfrac{n(n+1)}{2}$

6) Encontrar una fórmula$ a_n$ para el$n^{\text{th}}$ término de la secuencia aritmética cuyo primer término es$ a_1=1$ tal que$ a_{n−1}−a_n=17$ para$ n≥1$.

7) Encontrar una fórmula$ a_n$ para el$n^{\text{th}}$ término de la secuencia aritmética cuyo primer término es$ a_1=−3$ tal que$ a_{n−1}−a_n=4$ para$ n≥1$.

Contestar: $ a_n=4n−7$

8) Encontrar una fórmula$ a_n$ para el$n^{\text{th}}$ término de la secuencia geométrica cuyo primer término es$ a_1=1$ tal que$ \dfrac{a_{n+1}}{a_n}=10$ para$ n≥1$.

9) Encontrar una fórmula$ a_n$ para el$n^{\text{th}}$ término de la secuencia geométrica cuyo primer término es$ a_1=3$ tal que$ \dfrac{a_{n+1}}{a_n}=1/10$ para$ n≥1$.

Contestar: $ a_n=3.10^{1−n}=30.10^{−n}$

10) Encuentra una fórmula explícita para el$n^{\text{th}}$ término de la secuencia cuyos primeros términos son varios$ {0,3,8,15,24,35,48,63,80,99,…}.$ (Pista: Primero agrega uno a cada término.)

11) Encontrar una fórmula explícita para el$n^{\text{th}}$ término de la secuencia satisfactoria$ a_1=0$ y$ a_n=2a_{n−1}+1$ para$ n≥2$.

Contestar: $ a_n=2^n−1$

En los ejercicios 12 y 13, encuentra una fórmula para el término general$ a_n$ de cada una de las siguientes secuencias.

12)$ {1,0,−1,0,1,0,−1,0,…}$ (Pista: Encuentra dónde$\sin x$ toma estos valores)

13)$ {1,−1/3,1/5,−1/7,…}$

Contestar: $ a_n=\dfrac{(−1)^{n−1}}{2n−1}$

En los ejercicios 14-18, encuentra una función$ f(n)$ que identifique el$n^{\text{th}}$ término$ a_n$ de las siguientes secuencias definidas recursivamente, como$ a_n=f(n)$.

14)$ a_1=1$ y$ a_{n+1}=−a_n$ para$ n≥1$

15)$ a_1=2$ y$ a_{n+1}=2a_n$ para$ n≥1$

Contestar: $ f(n)=2^n$

16)$ a_1=1$ y$ a_{n+1}=(n+1)a_n$ para$ n≥1$

17)$ a_1=2$ y$ a_{n+1}=(n+1)a_n/2$ para$ n≥1$

Contestar: $f(n)=\dfrac{n!}{2^{n-2}}$

18)$ a_1=1$ y$ a_{n+1}=a_n/2^n$ para$ n≥1$

En los ejercicios 19 - 22, trazar los primeros$ N$ términos de la secuencia dada. Indique si la evidencia gráfica sugiere que la secuencia converge o diverge.

19) [T]$ a_1=1, a_2=2$, y para$ n≥2, a_n=\frac{1}{2}(a_{n−1}+a_{n−2})$;$ N=30$

Contestar

Los términos oscilan arriba$ 5/3$ y abajo y parecen converger a$ 5/3$.

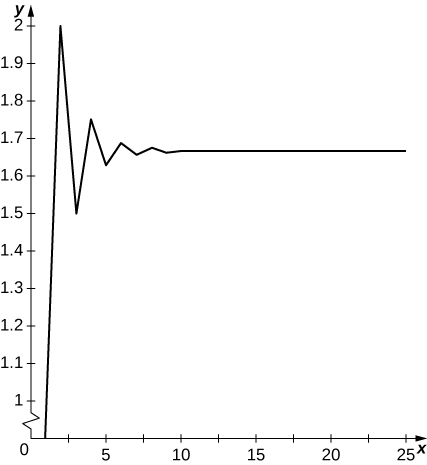
20) [T]$ a_1=1, a_2=2, a_3=3$ y para$ n≥4, a_n=\frac{1}{3}(a_{n−1}+a_{n−2}+a_{n−3}), N=30$

21) [T]$ a_1=1, a_2=2$, y para$ n≥3, a_n=\sqrt{a_{n−1}a_{n−2}}; N=30$

Contestar

Los términos oscilan arriba$ y≈1.57..$ y abajo y parecen converger a un límite.

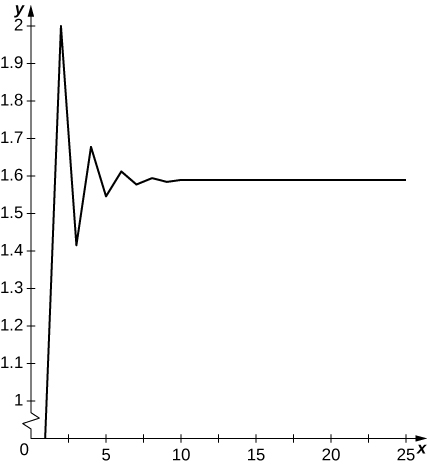
22) [T]$ a_1=1, a_2=2, a_3=3$, y para$ n≥4, a_n=\sqrt{a_{n−1}a_{n−2}a_{n−3}}; N=30$

En los ejercicios 23 a 16, supongamos eso$\displaystyle \lim_{n→∞}a_n=1, $$\displaystyle \lim_{n→∞}b_n=−1$, y$ 0<−b_n<a_n$ para todos$ n$.

Utilizando esta información, evaluar cada uno de los siguientes límites, declarar que el límite no existe, o declarar que no hay suficiente información para determinar si el límite existe.

23)$\displaystyle \lim_{n→∞}3a_n−4b_n$

Contestar: $\displaystyle \lim_{n→∞}3a_n−4b_n \quad = \quad 7$

24)$\displaystyle \lim_{n→∞}\frac{1}{2}b_n−\frac{1}{2}a_n$

25)$\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n}$

Contestar: $\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n} \quad = \quad 0$

26)$\displaystyle \lim_{n→∞}\frac{a_n−b_n}{a_n+b_n}$

En los ejercicios 27 - 30, encuentra el límite de cada una de las siguientes secuencias, utilizando la regla de L'Hôpital cuando corresponda.

27)$ \dfrac{n^2}{2^n}$

Contestar: $\displaystyle \lim_{n→∞} \dfrac{n^2}{2^n} \quad = \quad 0$

28)$ \dfrac{(n−1)^2}{(n+1)^2}$

29)$ \dfrac{\sqrt{n}}{\sqrt{n+1}}$

Contestar: $\displaystyle \lim_{n→∞} \dfrac{\sqrt{n}}{\sqrt{n+1}} \quad = \quad 1 $

30)$ n^{1/n}$ (Pista:$ n^{1/n}=e^{\frac{1}{n}\ln n})$

En los ejercicios 31 - 37, indique si cada secuencia está delimitada y si eventualmente es monótona, creciente o decreciente.

31)$ n/2^n, n≥2$

Contestar: acotado, decreciente para$ n≥1$

32)$ \ln\left(1+\dfrac{1}{n}\right)$

33)$ \sin n$

Contestar: acotado, no monótona

34)$ \cos(n^2)$

35)$ n^{1/n}, \quad n≥3$

Contestar: acotado, decreciente

36)$ n^{−1/n}, \quad n≥3$

37)$ \tan n$

Contestar: no monótona, no acotada

En los ejercicios 38 - 39, determinar si la secuencia dada tiene un límite. Si lo hace, encuentra el límite.

38)$ a_1=\sqrt{2}, a_2=\sqrt{2\sqrt{2}}. a_3=\sqrt{2\sqrt{2\sqrt{2}}}$ etc.

39)$ a_1=3, a_n=\sqrt{2a_{n−1}}, n=2,3,….$

Contestar: $ a_n$es decreciente y delimitado por debajo por$2$. El límite a debe$ a=\sqrt{2a}$ satisfacerlo$ a=2$, independientemente del valor inicial.

Usa el Teorema de Squeeze para encontrar el límite de cada secuencia en los ejercicios 40 - 43.

40)$ n\sin(1/n)$

41)$ \dfrac{\cos(1/n)−1}{1/n}$

Contestar: $0$

42)$ a_n=\dfrac{n!}{n^n}$

43)$ a_n=\sin n \sin(1/n)$

Contestar: $ 0$desde$|\sin x|≤|x|$ y$ |\sin x|≤1$ así$ −\dfrac{1}{n}≤a_n≤\dfrac{1}{n})$.

Para las secuencias en los ejercicios 44 y 45, graficar los primeros$ 25$ términos de la secuencia y establecer si la evidencia gráfica sugiere que la secuencia converge o diverge.

44) [T]$ a_n=\sin n$

45) [T]$ a_n=\cos n$

Contestar

La gráfica oscila y sugiere que no hay límite.

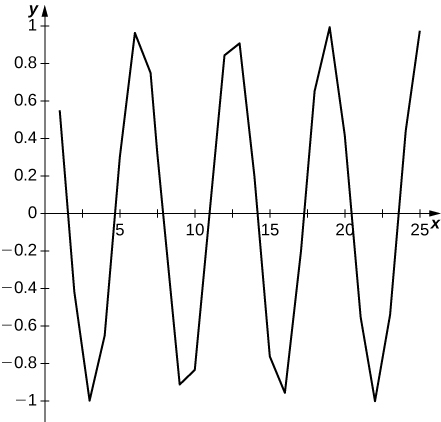
En los ejercicios 46 - 52, determinar el límite de la secuencia o mostrar que la secuencia diverge. Si converge, encuentra su límite.

46)$ a_n=\tan^{−1}(n^2)$

47)$ a_n=(2n)^{1/n}−n^{1/n}$

Contestar: $ n^{1/n}→1$y$ 2^{1/n}→1,$ así$ a_n→0$

48)$ a_n=\dfrac{\ln(n^2)}{\ln(2n)}$

49)$ a_n=\left(1−\frac{2}{n}\right)^n$

Contestar: Ya que$ (1+1/n)^n→e$, uno tiene$ (1−2/n)^n≈(1+k)^{−2k}→e^{−2}$ como$ k→∞.$

50)$ a_n=\ln\left(\dfrac{n+2}{n^2−3}\right)$

51)$ a_n=\dfrac{2^n+3^n}{4^n}$

Contestar: $ 2^n+3^n≤2⋅3^n$y$ 3^n/4^n→0$ como$ n→∞$, a fin$ a_n→0$ de$ n→∞.$

52)$ a_n=\dfrac{(1000)^n}{n!}$

53)$ a_n=\dfrac{(n!)^2}{(2n)!}$

Contestar: $ \dfrac{a_{n+1}}{a_n}=n!/(n+1)(n+2)⋯(2n) =\dfrac{1⋅2⋅3⋯n}{(n+1)(n+2)⋯(2n)}<1/2^n$. En particular,$ a_{n+1}/a_n≤1/2$, así$ a_n→0$ como$ n→∞$.

El método de Newton busca aproximar una solución$ f(x)=0$ que comience con una aproximación inicial$ x_0$ y defina sucesivamente una secuencia$ x_{n+1}=x_n−\dfrac{f(x_n)}{f′(x_n)}$. Para la elección dada de$ f$ y$ x_0$, escriba la fórmula para$ x_{n+1}$. Si la secuencia parece converger, dé una fórmula exacta para la solución$ x$, luego identifique el límite$ x$ exacto a cuatro decimales y el más pequeño$ n$ tal que$ x_n$ concuerde con$ x$ hasta cuatro decimales.

54) [T]$ f(x)=x^2−2,\quad x_0=1$

55) [T]$ f(x)=(x−1)^2−2,\quad x_0=2$

Contestar: \ (x_ {n+1} =x_n− ((x_n−1) ^2−2) /2 (x_n−1);\;
x=1+\ sqrt {2},\; x≈2.4142,\; n=5\)

56) [T]$ f(x)=e^x−2, \quad x_0=1$

57) [T]$ f(x)=\ln x−1,\quad x_0=2$

Contestar: \ (x_ {n+1} =x_n−x_n (\ ln (x_n) −1);\;
x=e,\; x≈2.7183,\; n=5\)

58) [T] Supongamos que comienza con un litro de vinagre y elimina repetidamente$0.1$ L, reemplaza con agua, mezcla y repite.

a. Encontrar una fórmula para la concentración después de$ n$ los pasos.

b. ¿Después de cuántos pasos contiene la mezcla menos que$ 10\%$ vinagre?

59) [T] Un lago contiene inicialmente$ 2000$ peces. Supongamos que ante la ausencia de depredadores u otras causas de remoción, la población de peces aumenta$ 6\%$ cada mes. Sin embargo, teniendo en cuenta todas las causas, los$ 150$ peces se pierden cada mes.

a. Explique por qué la población de peces después de$ n$ meses es modelada por$ P_n=1.06P_{n−1}−150$ con$ P_0=2000$.

b. ¿Cuántos peces habrá en el estanque después de un año?

Contestar: a. Sin pérdidas, la población obedecería$ P_n=1.06P_{n−1}$. La resta de$ 150$ cuentas por pérdidas de peces.
b. Después de$ 12$ meses, tenemos$ P_{12}≈1494.$

60) [T] Una cuenta bancaria gana$ 5\%$ intereses compuestos mensualmente. Supongamos que inicialmente$ $1000$ se deposita en la cuenta, pero que$ $10$ se retira cada mes.

a. Demostrar que el monto en la cuenta después de$ n$ meses es$ A_n=(1+.05/12)A_{n−1}−10; \; A_0=1000.$

b. ¿Cuánto dinero habrá en la cuenta tras$ 1$ año?

c. ¿La cantidad aumenta o disminuye?

d. Supongamos que en vez de$ $10$, se retira una cantidad fija de$ d$ dólares cada mes. Encuentra un valor de$ d$ tal manera que el monto en la cuenta después de cada mes permanezca$ $1000$.

e. ¿Qué sucede si$ d$ es mayor que esta cantidad?

61) [T] Un estudiante obtiene un préstamo universitario de$ $10,000$ a una tasa porcentual anual de$ 6\%,$ mensual compuesto.

a. si el estudiante realiza pagos$ $100$ mensuales, ¿cuánto debe el estudiante después de$ 12$ meses?

b. ¿Después de cuántos meses se pagará el préstamo?

Contestar: a. El estudiante debe$ $9383$ después de$ 12$ meses.
b. El préstamo se pagará en su totalidad después de$ 139$ meses o once años y medio.

62) [T] Considerar una serie que combine crecimiento geométrico y disminución aritmética. Vamos$ a_1=1$. Fijar$ a>1$ y$ 0<b<a$. Establecer$ a_{n+1}=a.a_n−b.$ Encontrar una fórmula para$ a_{n+1}$ en términos de$ a_n, a$, y$ b$ y una relación entre$ a$ y$ b$ tal que$ a_n$ converja.

63) [T] La representación binaria$ x=0.b_1b_2b_3...$ de un número$ x$ entre$ 0$ y se$ 1$ puede definir de la siguiente manera. Deja$ b_1=0$ si$ x<1/2$ y$ b_1=1$ si$ 1/2≤x<1.$ Let$ x_1=2x−b_1$. Que$ b_2=0$ si$ x_1<1/2$ y$ b_2=1$ si$ 1/2≤x<1$. Dejar$ x_2=2x_1−b_2$ y en general,$ x_n=2x_{n−1}−b_n$ y$ b_{n−}1=0$ si$ x_n<1/2$ y$ b_{n−1}=1$ si$ 1/2≤x_n<1$. Encuentra la expansión binaria de$ 1/3$.

Contestar: $ b_1=0, x_1=2/3, b_2=1, x_2=4/3−1=1/3,$por lo que el patrón se repite, y$ 1/3=0.010101….$

64) [T] Encontrar una aproximación para$ π$, establecer$ a_0=\sqrt{2+1}, a_1=\sqrt{2+a_0}$, y, en general,$ a_{n+1}=\sqrt{2+a_n}$. Por último, establecer$ p_n=3.2^n\sqrt{2−a_n}$. Encuentra los primeros diez términos de$ p_n$ y compara los valores con$ π$.

Para los dos ejercicios siguientes, asuma que tienes acceso a un programa informático o fuente de Internet que puede generar una lista de ceros y unos de cualquier longitud deseada. Los generadores de números pseudo-aleatorios (PRNG) juegan un papel importante en la simulación del ruido aleatorio en sistemas físicos al crear secuencias de ceros y unos que aparecen como el resultado de voltear una moneda repetidamente. Uno de los tipos más simples de PRNG define recursivamente una secuencia de$ N$ números enteros de aspecto aleatorio$ a_1,a_2,…,a_N$ fijando dos enteros especiales$ (K$$ M$ y dejando$ a_{n+1}$ ser el resto después de$ K.a_n$ dividirlos en$ M$, luego crea una secuencia de bits de ceros y unos cuya $n^{\text{th}}$término$ b_n$ es igual a uno si$ a_n$ es impar e igual a cero si$ a_n$ es par. Si los bits$ b_n$ son pseudo-aleatorios, entonces el comportamiento de su promedio$ (b_1+b_2+⋯+b_N)/N$ debería ser similar al comportamiento de los promedios de bits realmente generados aleatoriamente.

65) [T] Comenzando con$ K=16,807$ y$ M=2,147,483,647$, usando diez valores iniciales diferentes de$ a_1$, computar secuencias de bits$ b_n$ hasta$ n=1000,$ y comparar sus promedios con diez secuencias generadas por un generador de bits aleatorios.

Contestar: Para los valores iniciales$ a_1=1, a_2=2,…, a_1=10,$ los promedios de bits correspondientes calculados por el método indicado son$ 0.5220, 0.5000, 0.4960, 0.4870, 0.4860, 0.4680, 0.5130, 0.5210, 0.5040,$ y$ 0.4840$. Aquí un ejemplo de diez promedios correspondientes de cadenas de$ 1000$ bits generados por un generador de números aleatorios: No$ 0.4880, 0.4870, 0.5150, 0.5490, 0.5130, 0.5180, 0.4860, 0.5030, 0.5050, 0.4980.$ hay patrón real en ninguno de los tipos de promedio. Los promedios generados por números aleatorios oscilan entre$ 0.4860$ y$ 0.5490$, un rango de$ 0.0630$, mientras que los promedios de bits de PRNG calculados oscilan entre$ 0.4680$ y$ 0.5220$, un rango de$ 0.0540.$

66) [T] Encuentra los primeros$ 1000$ dígitos de$ π$ usar ya sea un programa de computadora o un recurso de Internet. Crea una secuencia de bits$ b_n$ dejando$ b_n=1$ si el$n^{\text{th}}$ dígito de$ π$ es impar y$ b_n=0$ si el$n^{\text{th}}$ dígito de$ π$ es par. Calcule el valor promedio de$ b_n$ y el valor promedio de$ d_n=|b_{n+1}−b_n|, n=1,...,999.$ ¿La secuencia$ b_n$ parece aleatoria? ¿Las diferencias entre elementos sucesivos de$ b_n$ aparecen aleatorias?