11.3: Coordenadas polares
- Page ID
- 116192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Localizar puntos en un plano usando coordenadas polares.
- Convertir puntos entre coordenadas rectangulares y polares.
- Esbozar curvas polares a partir de ecuaciones dadas.
- Convertir ecuaciones entre coordenadas rectangulares y polares.
- Identificar simetría en curvas polares y ecuaciones.
El sistema de coordenadas rectangulares (o plano cartesiano) proporciona un medio para mapear puntos a pares ordenados y pares ordenados a puntos. Esto se denomina mapeo uno a uno desde puntos en el plano a pares ordenados. El sistema de coordenadas polares proporciona un método alternativo para mapear puntos a pares ordenados. En esta sección vemos que en algunas circunstancias, las coordenadas polares pueden ser más útiles que las coordenadas rectangulares.
Definición de coordenadas polares
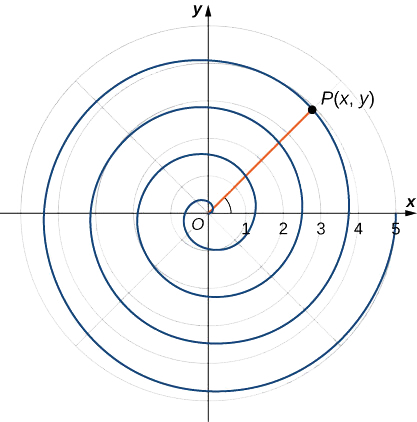
Para encontrar las coordenadas de un punto en el sistema de coordenadas polares, considere Figura\(\PageIndex{1}\). El punto\(P\) tiene coordenadas cartesianas\((x,y)\). El segmento de línea que conecta el origen con el punto\(P\) mide la distancia desde el origen hasta\(P\) y tiene longitud\(r\). El ángulo entre el eje x positivo y el segmento de línea tiene medida\(θ\). Esta observación sugiere una correspondencia natural entre el par de coordenadas\((x,y)\) y los valores\(r\) y\(θ\). Esta correspondencia es la base del sistema de coordenadas polares. Tenga en cuenta que cada punto en el plano cartesiano tiene dos valores (de ahí el término par ordenado) asociados a él. En el sistema de coordenadas polares, cada punto también tiene dos valores asociados a él:\(r\) y\(θ\).
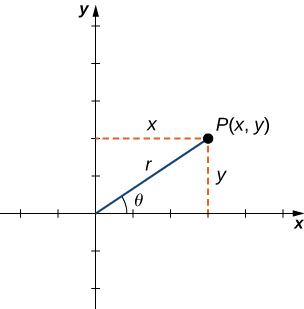
Usando trigonometría de triángulo rectángulo, las siguientes ecuaciones son ciertas para el punto\(P\):
\[\cos θ=\dfrac{x}{r}\text{ so }x=r\cos θ \nonumber \]
\[\sin θ=\dfrac{y}{r}\text{ so }y=r\sin θ. \nonumber \]
Además,
\[r^2=x^2+y^2 \nonumber \]
y
\[\tan θ=\dfrac{y}{x}. \nonumber \]
Por lo tanto, cada punto\((x,y)\) en el sistema de coordenadas cartesianas se puede representar como un par ordenado\((r,θ)\) en el sistema de coordenadas polares. La primera coordenada se llama coordenada radial y la segunda coordenada se llama coordenada angular. Cada punto del plano se puede representar en esta forma.
Tenga en cuenta que la ecuación\(\tan θ=y/x\) tiene un número infinito de soluciones para cualquier par ordenado\((x,y)\). Sin embargo, si restringimos las soluciones a valores entre\(0\) y\(2π\) entonces podemos asignar una solución única al cuadrante en el que\((x,y)\) se encuentra el punto original. Entonces el valor correspondiente de\(r\) es positivo, entonces\(r^2=x^2+y^2\).
Dado un punto\(P\) en el plano con coordenadas cartesianas\((x,y)\) y coordenadas polares\((r,θ)\), las siguientes fórmulas de conversión son verdaderas:
\[\begin{align} x &=r\cos θ \label{eq1} \\[4pt] y &=r\sin θ \label{eq2}\end{align} \]
y
\[\begin{align} r^2 &= x^2+y^2 \label{eq3}\\[4pt] \tan θ &=\dfrac{y}{x} \label{eq4}\end{align}. \]
Estas fórmulas se pueden utilizar para convertir de coordenadas rectangulares a polares o de polares a rectangulares. Observe que la Ecuación\ ref {eq3} es el teorema de Pitágoras. (Figura\(\PageIndex{1}\)).
Convierte cada uno de los siguientes puntos en coordenadas polares.
- \((1,1)\)
- \((−3,4)\)
- \((0,3)\)
- \((5\sqrt{3},−5)\)
Convierte cada uno de los siguientes puntos en coordenadas rectangulares.
- \((3,π/3)\)
- \((2,3π/2)\)
- \((6,−5π/6)\)
Solución
a. Uso\(x=1\) y\(y=1\) en la Ecuación\ ref {eq3}:
\[\begin{align*} r^2 &=x^2+y^2 \\[4pt] &=1^2+1^2 \\ r &=\sqrt{2} \end{align*} \nonumber \]
y vía Ecuación\ ref {eq4}
\[\begin{align*} \tan θ &= \dfrac{y}{x} = \dfrac{1}{1}=1 \\[4pt] θ &=\dfrac{π}{4}. \end{align*}\]
Por lo tanto, este punto se puede representar como\((\sqrt{2},\dfrac{π}{4})\) en coordenadas polares.
b. Uso\(x=−3\) y\(y=4\) en la Ecuación\ ref {eq3}:
\[\begin{align*} r^2 &= x^2+y^2=(−3)^2+(4)^2 \\[4pt] r&=5 \end{align*}\]
y vía Ecuación\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=−\dfrac{4}{3}\)
\(θ=\arctan(-\dfrac{4}{3})+π≈2.21.\)
Por lo tanto, este punto se puede representar como\((5,2.21)\) en coordenadas polares.
c. Uso\(x=0\) y\(y=3\) en Ecuación\ ref {eq3}:
\(r^2=x^2+y^2=(3)^2+(0)^2=9+0\)\(r=3\)
y vía Ecuación\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{3}{0}\).
La aplicación directa de la segunda ecuación conduce a la división por cero. Graficar el punto\((0,3)\) en el sistema de coordenadas rectangulares revela que el punto se encuentra en el eje y positivo. El ángulo entre el eje x positivo y el eje y positivo es\(\dfrac{π}{2}\). Por lo tanto, este punto se puede representar como\((3,\dfrac{π}{2})\) en coordenadas polares.
d. Uso\(x=5\sqrt{3}\) y\(y=−5\) en la Ecuación\ ref {eq3}:
\(r^2=x^2+y^2=(5\sqrt{3})^2+(−5)^2=75+25\)
\(r=10\)
y vía Ecuación\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{−5}{5\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\)
\(θ=−\dfrac{π}{6}\).
Por lo tanto, este punto se puede representar como\((10,−\dfrac{π}{6})\) en coordenadas polares.
e. Uso\(r=3\) y\(θ=\dfrac{π}{3}\) en la Ecuación\ ref {eq1}:
\(x=r\cos θ=3\cos(\dfrac{π}{3})=3(\dfrac{1}{2})=\dfrac{3}{2}\)
y
\(y=r\sin θ=3\sin(\dfrac{π}{3})=3(\dfrac{\sqrt{3}}{2})=\dfrac{3\sqrt{3}}{2}\).
Por lo tanto, este punto se puede representar como\((\dfrac{3}{2},\dfrac{3\sqrt{3}}{2})\) en coordenadas rectangulares.
f. Uso\(r=2\) y\(θ=\dfrac{3π}{2}\) en la Ecuación\ ref {eq1}:
\(x=r\cos θ=2\cos(\dfrac{3π}{2})=2(0)=0\)
y
\(y=r\sin θ=2\sin(\dfrac{3π}{2})=2(−1)=−2.\)
Por lo tanto, este punto se puede representar como\((0,−2)\) en coordenadas rectangulares.
g. Uso\(r=6\) y\(θ=−\dfrac{5π}{6}\) en la Ecuación\ ref {eq1}:
\(x=r\cos θ=6\cos(−\dfrac{5π}{6})=6(−\dfrac{\sqrt{3}}{2})=−3\sqrt{3}\)
y
\(y=r\sin θ=6\sin(−\dfrac{5π}{6})=6(−\dfrac{1}{2})=−3\).
Por lo tanto, este punto se puede representar como\((−3\sqrt{3},−3)\) en coordenadas rectangulares.
Convertir\((−8,−8)\) en coordenadas polares y\((4,\dfrac{2π}{3})\) en coordenadas rectangulares.
- Pista
-
Usa la Ecuación\ ref {eq3} y la Ecuación\ ref {eq1}. Asegúrese de revisar el cuadrante al calcular\(θ\).
- Responder
-
\((8\sqrt{2},\dfrac{5π}{4})\)y\((−2,2\sqrt{3})\)
La representación polar de un punto no es única. Por ejemplo, las coordenadas polares\((2,\dfrac{π}{3})\) y\((2,\dfrac{7π}{3})\) ambas representan el punto\((1,\sqrt{3})\) en el sistema rectangular. Además, el valor de r puede ser negativo. Por lo tanto, el punto con coordenadas polares\((−2,\dfrac{4π}{3})\) también representa el punto\((1,\sqrt{3})\) en el sistema rectangular, como podemos ver usando la Ecuación\ ref {eq1}:
\[x=r\cos θ=−2\cos(\dfrac{4π}{3})=−2(−\dfrac{1}{2})=1 \nonumber \]
y
\[y=r\sin θ=−2\sin(\dfrac{4π}{3})=−2(−\dfrac{\sqrt{3}}{2})=\sqrt{3}. \nonumber \]
Cada punto del plano tiene un número infinito de representaciones en coordenadas polares. Sin embargo, cada punto del plano tiene una sola representación en el sistema de coordenadas rectangulares.
Obsérvese que la representación polar de un punto en el plano también tiene una interpretación visual. En particular,\(r\) es la distancia dirigida que el punto se encuentra desde el origen, y\(θ\) mide el ángulo que el segmento de línea desde el origen hasta el punto hace con el\(x\) eje positivo. Los ángulos positivos se miden en sentido contrario a las agujas del reloj y los ángulos negativos se miden en sentido horario. El sistema de coordenadas polares aparece en la Figura\(\PageIndex{2}\).
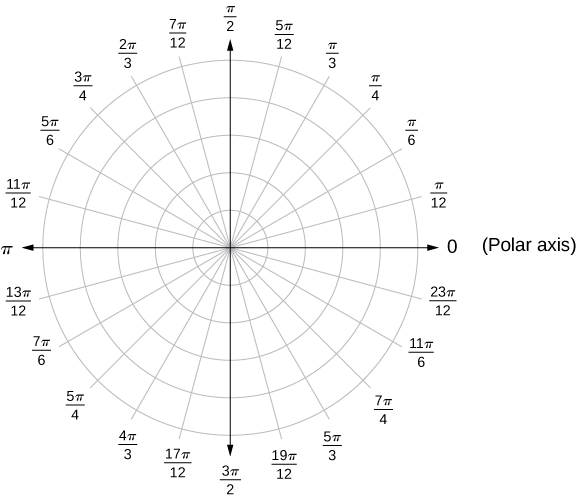
El segmento de línea que comienza desde el centro de la gráfica que va hacia la derecha (llamado eje x positivo en el sistema cartesiano) es el eje polar. El punto central es el polo, u origen, del sistema de coordenadas, y corresponde a\(r=0\). El círculo más interno que se muestra en la Figura\(\PageIndex{2}\) contiene todos los puntos a una distancia de 1 unidad del polo, y está representado por la ecuación\(r=1\). Entonces\(r=2\) está el conjunto de puntos a 2 unidades del poste, y así sucesivamente. Los segmentos de línea que emanan del polo corresponden a ángulos fijos. Para trazar un punto en el sistema de coordenadas polares, comience con el ángulo. Si el ángulo es positivo, entonces mida el ángulo desde el eje polar en sentido contrario a las agujas del reloj. Si es negativo, entonces mídalo en sentido horario. Si el valor de r es positivo, mueva esa distancia a lo largo del rayo terminal del ángulo. Si es negativo, muévase a lo largo del rayo que está opuesto al rayo terminal del ángulo dado.
Trazar cada uno de los siguientes puntos en el plano polar.
- \((2,\dfrac{π}{4})\)
- \((−3,\dfrac{2π}{3})\)
- \((4,\dfrac{5π}{4})\)
Solución
Los tres puntos se trazan en la Figura\(\PageIndex{3}\).

Trama\((4,\dfrac{5π}{3})\) y\((−3,−\dfrac{7π}{2})\) en el plano polar.
- Pista
-
Comience con\(θ\), luego use\(r\).
- Responder
-

Curvas polares
Ahora que sabemos trazar puntos en el sistema de coordenadas polares, podemos discutir cómo trazar curvas. En el sistema de coordenadas rectangulares, podemos graficar una función\(y=f(x)\) y crear una curva en el plano cartesiano. De manera similar, podemos graficar una curva que es generada por una función\(r=f(θ)\).
La idea general detrás de graficar una función en coordenadas polares es la misma que graficar una función en coordenadas rectangulares. Comience con una lista de valores para la variable independiente (\(θ\)en este caso) y calcule los valores correspondientes de la variable dependiente\(r\). Este proceso genera una lista de pares ordenados, los cuales pueden ser trazados en el sistema de coordenadas polares. Por último, conecta los puntos, y aprovecha cualquier patrón que pueda aparecer. La función puede ser periódica, por ejemplo, lo que indica que solo se necesita un número limitado de valores para la variable independiente.
- Crea una tabla con dos columnas. La primera columna es para\(θ\), y la segunda columna es para\(r\).
- Crear una lista de valores para\(θ\).
- Calcular los\(r\) valores correspondientes para cada uno\(θ\).
- Trazar cada par ordenado\((r,θ)\) en los ejes de coordenadas.
- Conecta los puntos y busca un patrón.
Grafica la curva definida por la función\(r=4\sin θ\). Identificar la curva y reescribir la ecuación en coordenadas rectangulares.
Solución
Debido a que la función es un múltiplo de una función sinusoidal, es periódica con punto\(2π\), así que usa valores para\(θ\) entre\(0\) y\(2π\). El resultado de los pasos 1—3 aparece en la siguiente tabla. En la figura se\(\PageIndex{4}\) muestra la gráfica basada en esta tabla.
| \(θ\) | \(r=4\sin θ\) | \(θ\) | \(r=4\sin θ\) |
|---|---|---|---|
| \ (θ\)” style="vertical-align:middle; ">0 | \ (r=4\ sin θ\)” style="vertical-align:middle; ">0 | \ (θ\)” style="vertical-align:middle; ">\(π\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">0 |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{π}{6}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">2 | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{7π}{6}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(-2\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{π}{4}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(2\sqrt{2}≈2.8\) | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{5π}{4}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(−2\sqrt{2}≈−2.8\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{π}{3}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(2\sqrt{3}≈3.4\) | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{4π}{3}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(−2\sqrt{3}≈−3.4\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{π}{2}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">4 | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{3π}{2}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(-4\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{2π}{3}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(2\sqrt{3}≈3.4\) | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{5π}{3}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(−2\sqrt{3}≈−3.4\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{3π}{4}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(2\sqrt{2}≈2.8\) | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{7π}{4}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">\(−2\sqrt{2}≈−2.8\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{5π}{6}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">2 | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{11π}{6}\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">−2 |
| \ (θ\)” style="vertical-align:middle; "> | \ (r=4\ sin θ\)” style="vertical-align:middle; "> | \ (θ\)” style="vertical-align:middle; ">\(2π\) | \ (r=4\ sin θ\)” style="vertical-align:middle; ">0 |
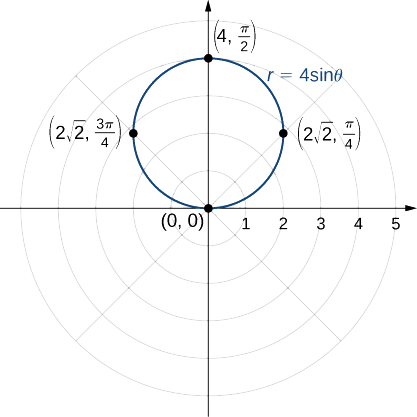
Esta es la gráfica de un círculo. La ecuación se\(r=4\sin θ\) puede convertir en coordenadas rectangulares multiplicando primero ambos lados por\(r\). Esto da la ecuación\(r^2=4r\sin θ.\) Siguiente utilizar los hechos que\(r^2=x^2+y^2\) y\(y=r\sin θ\). Esto da\(x^2+y^2=4y\). Para poner esta ecuación en forma estándar, resta\(4y\) de ambos lados de la ecuación y completa el cuadrado:
\[\begin{align*} x^2+y^2−4y &= 0 \\[4pt] x^2+(y^2−4y) &= 0 \\[4pt] x^2+(y^2−4y+4) &= 0+4 \\[4pt] x^2+(y−2)^2&=4 \end{align*}\]
Esta es la ecuación de un círculo con radio 2 y centro\((0,2)\) en el sistema de coordenadas rectangulares.
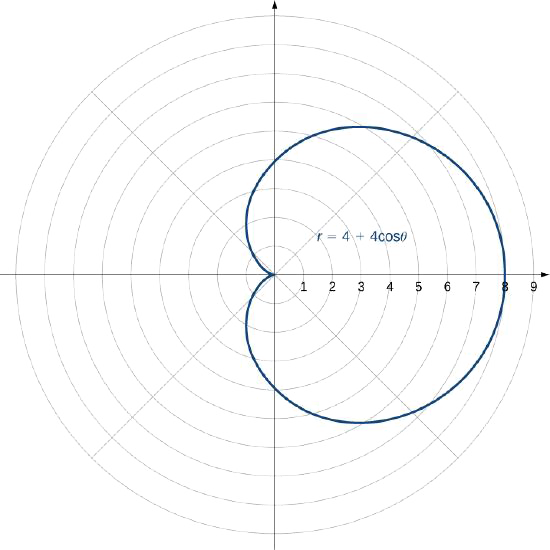
Crear una gráfica de la curva definida por la función\(r=4+4\cos θ\).
- Pista
-
Siga la estrategia de resolución de problemas para crear una gráfica en coordenadas polares.
- Responder
-
El nombre de esta forma es cardioide, que estudiaremos más adelante en esta sección.
La gráfica en Ejemplo\(\PageIndex{3}\) era la de un círculo. La ecuación del círculo se puede transformar en coordenadas rectangulares usando las fórmulas de transformación de coordenadas en la Ecuación\ ref {eq1}. Ejemplo\(\PageIndex{4}\) da algunos ejemplos más de funciones para transformar de coordenadas polares a rectangulares.
Reescribe cada una de las siguientes ecuaciones en coordenadas rectangulares e identifica la gráfica.
- \(θ=\dfrac{π}{3}\)
- \(r=3\)
- \(r=6\cos θ−8\sin θ\)
Solución:
a. Toma la tangente de ambos lados. Esto da\(\tan θ=\tan(π/3)=\sqrt{3}\) .Ya que\(\tan θ=y/x\) podemos sustituir el lado izquierdo de esta ecuación por\(y/x\). Esto da\(y/x=\sqrt{3}\), que se puede reescribir como\(y=x\sqrt{3}\). Esta es la ecuación de una línea recta que pasa por el origen con pendiente\(\sqrt{3}\). En general, cualquier ecuación polar de la forma\(θ=K\) representa una línea recta a través del polo con pendiente igual a\(\tan K\).
b. Primero, cuadrar ambos lados de la ecuación. Esto da\(r^2=9.\) Siguiente reemplazar\(r^2\) con\(x^2+y^2\). Esto da la ecuación\(x^2+y^2=9\), que es la ecuación de un círculo centrado en el origen con radio 3. En general, cualquier ecuación polar de la forma\(r=k\) donde k es una constante positiva representa un círculo de radio k centrado en el origen. (Nota: al cuadrar ambos lados de una ecuación es posible introducir nuevos puntos involuntariamente. Esto siempre se debe tomar en consideración. No obstante, en este caso no introducimos nuevos puntos. Por ejemplo,\((−3,\dfrac{π}{3})\) es el mismo punto que\((3,\dfrac{4π}{3})\).)
c. Multiplicar ambos lados de la ecuación por\(r\). Esto lleva a\(r^2=6r\cos θ−8r\sin θ\). Siguiente usa las fórmulas
\(r^2=x^2+y^2,x=r\cos θ,y=r\sin θ.\)
Esto da
\(r^2=6(r\cos θ)−8(r\sin θ)\)
\(x^2+y^2=6x−8y.\)
Para poner esta ecuación en forma estándar, primero mueve las variables del lado derecho de la ecuación al lado izquierdo, luego completa el cuadrado.
\(x^2+y^2=6x−8y\)
\(x^2−6x+y^2+8y=0\)
\((x^2−6x)+(y^2+8y)=0\)
\((x^2−6x+9)+(y^2+8y+16)=9+16\)
\((x−3)^2+(y+4)^2=25.\)
Esta es la ecuación de un círculo con centro en\((3,−4)\) y radio 5. Observe que el círculo pasa por el origen ya que el centro está a 5 unidades de distancia.
Reescribir la ecuación\(r=\sec θ\tan θ\) en coordenadas rectangulares e identificar su gráfica.
- Pista
-
Convierte a seno y coseno, luego multiplica ambos lados por coseno.
- Responder
-
\(y=x^2\), que es la ecuación de una parábola que se abre hacia arriba.
Ahora hemos visto varios ejemplos de gráficos de dibujo de curvas definidas por ecuaciones polares. Un resumen de algunas curvas comunes se da en las tablas siguientes. En cada ecuación, a y b son constantes arbitrarias.
Un cardioide es un caso especial de un limaçon (pronunciado “lee-mah-son”), en el que\(a=b\) o\(a=−b\). La rosa es una curva muy interesante. Observe que la gráfica de\(r=3\sin 2θ\) tiene cuatro pétalos. Sin embargo, la gráfica de\(r=3\sin 3θ\) tiene tres pétalos como se muestra.
Si el coeficiente de\(θ\) es par, la gráfica tiene el doble de pétalos que el coeficiente. Si el coeficiente de\(θ\) es impar, entonces el número de pétalos es igual al coeficiente. Se le anima a explorar por qué sucede esto. Incluso surgen gráficas más interesantes cuando el coeficiente de no\(θ\) es un entero. Por ejemplo, si es racional, entonces la curva se cierra; es decir, finalmente termina donde comenzó (Figura\(\PageIndex{8a}\)). Sin embargo, si el coeficiente es irracional, entonces la curva nunca se cierra (Figura\(\PageIndex{8b}\)). Si bien puede parecer que la curva está cerrada, un examen más detenido revela que los pétalos justo por encima del eje x positivo son ligeramente más gruesos. Esto se debe a que el pétalo no coincide del todo con el punto de partida.
Dado que la curva definida por la gráfica de\(r=3\sin(πθ)\) nunca se cierra, la curva representada en la Figura\(\PageIndex{8b}\) es sólo una representación parcial. De hecho, este es un ejemplo de una curva de llenado de espacio. Una curva de relleno de espacio es aquella que de hecho ocupa un subconjunto bidimensional del plano real. En este caso la curva ocupa el círculo de radio 3 centrado en el origen.
Recordemos el nautilo de cámara introducido en el preludio capitular. Esta criatura muestra una espiral cuando se corta la mitad del caparazón exterior. Es posible describir una espiral usando coordenadas rectangulares. La figura\(\PageIndex{9}\) muestra una espiral en coordenadas rectangulares. ¿Cómo podemos describir matemáticamente esta curva?
Solución
A medida que el punto P se desplaza alrededor de la espiral en sentido contrario a las agujas del reloj, su distancia d desde el origen aumenta. Supongamos que la distancia d es un múltiplo constante k del ángulo\(θ\) que el segmento de línea OP hace con el eje x positivo. Por lo tanto\(d(P,O)=kθ\), dónde\(O\) está el origen. Ahora usa la fórmula de distancia y algo de trigonometría:
\(d(P,O)=kθ\)
\(\sqrt{(x−0)^2+(y−0)^2}=k\arctan(\dfrac{y}{x})\)
\(\sqrt{x^2+y^2}=k\arctan(\dfrac{y}{x})\)
\(\arctan(\dfrac{y}{x})=\dfrac{\sqrt{x^2+y^2}}{k}\)
\(y=x\tan(\dfrac{\sqrt{x^2+y^2}}{k})\).
Aunque esta ecuación describe la espiral, no es posible resolverla directamente para x ni para y, sin embargo, si usamos coordenadas polares, la ecuación se vuelve mucho más simple. En particular,\(d(P,O)=r\), y\(θ\) es la segunda coordenada. Por lo tanto, la ecuación para la espiral se convierte\(r=kθ\). Tenga en cuenta que cuando también\(θ=0\) tenemos\(r=0\), entonces la espiral emana del origen. Podemos eliminar esta restricción añadiendo una constante a la ecuación. Entonces la ecuación para la espiral se convierte\(r=a+kθ\) para constantes arbitrarias\(a\) y\(k\). Esto se conoce como una espiral de Arquímedes, después del matemático griego Arquímedes.
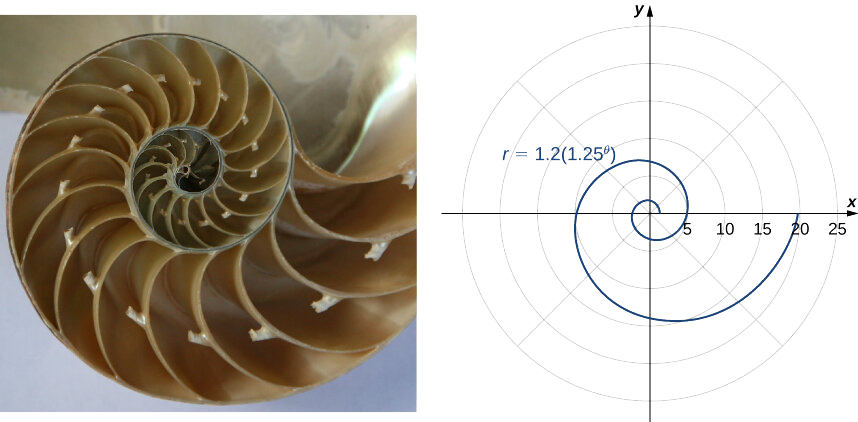
Otro tipo de espiral es la espiral logarítmica, descrita por la función\(r=a⋅b^θ\). Una gráfica de la función\(r=1.2(1.25^θ)\) se da en la Figura\(\PageIndex{10}\). Esta espiral describe la forma de concha del nautilus con cámaras.
Supongamos que se describe una curva en el sistema de coordenadas polares a través de la función\(r=f(θ)\). Ya que tenemos fórmulas de conversión de coordenadas polares a rectangulares dadas por
\[x=r\cos θ \nonumber \]
\[y=r\sin θ \nonumber \],
es posible reescribir estas fórmulas usando la función
\[x=f(θ)\cos θ \nonumber \]
\[y=f(θ)\sin θ. \nonumber \]
Este paso da una parametrización de la curva en coordenadas rectangulares utilizando\(θ\) como parámetro. Por ejemplo, la fórmula espiral\(r=a+bθ\) de Figura se convierte en
\[x=(a+bθ)\cos θ \nonumber \]
\[y=(a+bθ)\sin θ. \nonumber \]
Dejar\(θ\) variar de\(−∞\) a\(∞\) genera toda la espiral.
Simetría en coordenadas polares
Al estudiar la simetría de funciones en coordenadas rectangulares (es decir, en la forma\(y=f(x)\)), se habla de simetría con respecto al eje y y simetría con respecto al origen. En particular, si\(f(−x)=f(x)\) para todos\(x\) en el dominio de\(f\), entonces\(f\) es una función par y su gráfica es simétrica con respecto al eje y. Si\(f(−x)=−f(x)\) para todo x en el dominio de\(f\), entonces f es una función impar y su gráfica es simétrica con respecto al origen. Al determinar qué tipos de simetría exhibe una gráfica, podemos aprender más sobre la forma y apariencia de la gráfica. La simetría también puede revelar otras propiedades de la función que genera la gráfica. La simetría en curvas polares funciona de manera similar.
Considera una curva generada por la función\(r=f(θ)\) en coordenadas polares.
- La curva es simétrica alrededor del eje polar si por cada punto\((r,θ)\) de la gráfica, el punto también\((r,−θ)\) está en la gráfica. De igual manera, la ecuación\(r=f(θ)\) no cambia al reemplazarla\(θ\) con\(−θ\).
- La curva es simétrica alrededor del polo si por cada punto\((r,θ)\) de la gráfica, el punto también\((r,π+θ)\) está en la gráfica. Del mismo modo, la ecuación\(r=f(θ)\) no cambia cuando se reemplaza\(r\) con\(−r\), o\(θ\) con\(π+θ.\)
- La curva es simétrica respecto a la línea vertical\(θ=\dfrac{π}{2}\) si por cada punto\((r,θ)\) de la gráfica, el punto también\((r,π−θ)\) está en la gráfica. De igual manera, la ecuación\(r=f(θ)\) no cambia cuando\(θ\) es reemplazada por\(π−θ\).
En la siguiente tabla se muestran ejemplos de cada tipo de simetría.
Encuentra la simetría de la rosa definida por la ecuación\(r=3\sin(2θ)\) y crea una gráfica.
Solución
Supongamos que el punto\((r,θ)\) está en la gráfica de\(r=3\sin(2θ).\)
i. Para probar la simetría alrededor del eje polar, primero intente reemplazarlo\(θ\) con\(−θ\). Esto da\(r=3\sin(2(−θ))=−3\sin(2θ)\). Dado que esto cambia la ecuación original, esta prueba no se satisface. Sin embargo, volviendo a la ecuación original y reemplazando\(r\) con\(−r\) y\(θ\) con\(π−θ\) rendimientos
\[ \begin{align*} −r&=3\sin(2(π−θ)) \\[4pt] −r &=3\sin(2π−2θ) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3\sin2θ. \end{align*}\]
Multiplicando ambos lados de esta ecuación por\(−1\) da\(r=3\sin 2θ\), que es la ecuación original. Esto demuestra que la gráfica es simétrica con respecto al eje polar.
ii. Para probar la simetría con respecto al polo, primero reemplace\(r\) con\(−r\), que rinde\(−r=3\sin(2θ)\). Multiplicando ambos lados por\(−1\) da\(r=−3\sin(2θ)\), lo que no concuerda con la ecuación original. Por lo tanto, la ecuación no pasa la prueba para esta simetría. Sin embargo, volviendo a la ecuación original y reemplazando\(θ\) con\(θ+π\) da
\[ \begin{align*} r&=3\sin(2(θ+π)) \\[4pt] &=3\sin(2θ+2π) \\[4pt] &=3(\sin 2θ \cos 2π + \cos 2θ \sin 2π) \\[4pt] &=3\sin 2θ. \end{align*}\]
Dado que esto concuerda con la ecuación original, la gráfica es simétrica alrededor del polo.
iii. Para probar la simetría con respecto a la línea vertical\(θ=\dfrac{π}{2}\), primero reemplace ambos\(r\) con\(−r\) y\(θ\) con\(−θ\).
\[ \begin{align*} −r &=3\sin(2(−θ)) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3 \sin 2θ. \end{align*}\]
Multiplicando ambos lados de esta ecuación por\(−1\) da\(r=3\sin 2θ\), que es la ecuación original. Por lo tanto, la gráfica es simétrica respecto a la línea vertical\(θ=\dfrac{π}{2}\).
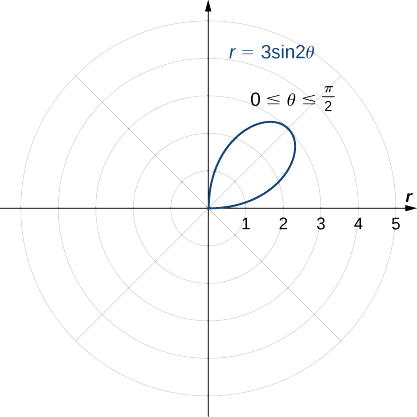
Esta gráfica tiene simetría con respecto al eje polar, el origen y la línea vertical que atraviesa el polo. Para graficar la función, tabular valores de\(θ\) entre\(0\) y\(π/2\) y luego reflejar la gráfica resultante.
| 0 | 0 |
| \(\dfrac{π}{6}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{4}\) | 3 |
| \(\dfrac{π}{3}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{2}\) | 0 |
Esto da un pétalo de la rosa, como se muestra en la siguiente gráfica.
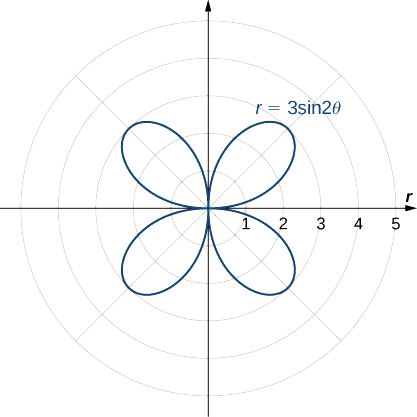
Reflejar esta imagen en los otros tres cuadrantes da la gráfica completa como se muestra.
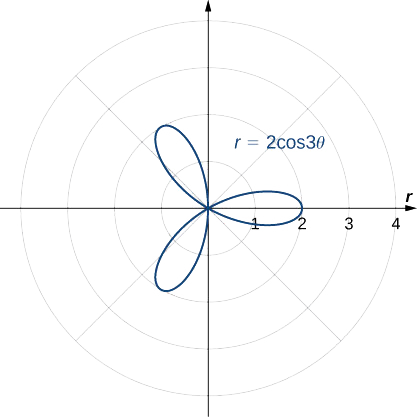
Determinar la simetría de la gráfica determinada por la ecuación\(r=2\cos(3θ)\) y crear una gráfica.
- Pista
-
Nota de uso.
- Responder
-
Simétrico con respecto al eje polar.
Conceptos clave
- El sistema de coordenadas polares proporciona una forma alternativa de ubicar puntos en el plano.
- Convertir puntos entre coordenadas rectangulares y polares usando las fórmulas
\[x=r\cos θ \text{ and } y=r\sin θ \nonumber \]
y
\[r=\sqrt{x^2+y^2} \text{ and} \tan θ=\dfrac{y}{x}. \nonumber \]
- Para esbozar una curva polar a partir de una función polar dada, haga una tabla de valores y aproveche las propiedades periódicas.
- Utilice las fórmulas de conversión para convertir ecuaciones entre coordenadas rectangulares y polares.
- Identificar simetría en curvas polares, que pueden ocurrir a través del polo, el eje horizontal o el eje vertical.
Glosario
- coordenada angular
- \(θ\)el ángulo formado por un segmento de línea que conecta el origen a un punto en el sistema de coordenadas polares con el eje radial positivo (x), medido en sentido antihorario
- cardioide
- una curva plana trazada por un punto en el perímetro de un círculo que está rodando alrededor de un círculo fijo del mismo radio; la ecuación de un cardioide es\(r=a(1+\sin θ)\) o\(r=a(1+\cos θ)\)
- limaçon
- la gráfica de la ecuación\(r=a+b\sin θ\) o\(r=a+b\cos θ.\) Si\(a=b\) entonces la gráfica es un cardioide
- eje polar
- el eje horizontal en el sistema de coordenadas polares correspondiente a\(r≥0\)
- sistema de coordenadas polares
- un sistema para localizar puntos en el plano. Las coordenadas son\(r\), la coordenada radial, y\(θ\), la coordenada angular
- ecuación polar
- una ecuación o función que relaciona la coordenada radial con la coordenada angular en el sistema de coordenadas polares
- polo
- el punto central del sistema de coordenadas polares, equivalente al origen de un sistema cartesiano
- coordenada radial
- \(r\)la coordenada en el sistema de coordenadas polares que mide la distancia desde un punto en el plano hasta el polo
- rosa
- gráfico de la ecuación polar\(r=a\cos 2θ\) o\(r=a\sin 2θ\) para una constante positiva\(a\)
- curva de llenado de espacio
- una curva que ocupa completamente un subconjunto bidimensional del plano real


