12.7E: Ejercicios para la Sección 12.7

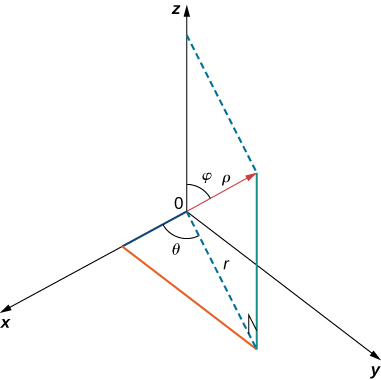
Utilice la siguiente figura como ayuda para identificar la relación entre los sistemas de coordenadas rectangulares, cilíndricos y esféricos.

Para los ejercicios 1 - 4, se dan las coordenadas cilíndricas\( (r,θ,z)\) de un punto. Encuentra las coordenadas rectangulares\( (x,y,z)\) del punto.

1)\( \left(4,\frac{π}{6},3\right)\)

Responder

\( (2\sqrt{3},2,3)\)

2)\( \left(3,\frac{π}{3},5\right)\)

3)\( \left(4,\frac{7π}{6},3\right)\)

Responder

\( (−2\sqrt{3},−2,3)\)

4)\( (2,π,−4)\)

Para los ejercicios 5 - 8, se dan\( (x,y,z)\) las coordenadas rectangulares de un punto. Encuentra las coordenadas cilíndricas\( (r,θ,z)\) del punto.

5)\( (1,\sqrt{3},2)\)

Responder

\( \left(2,\frac{π}{3},2\right)\)

6)\( (1,1,5)\)

7)\( (3,−3,7)\)

Responder

\( \left(3\sqrt{2},−\frac{π}{4},7\right)\)

8)\( (−2\sqrt{2},2\sqrt{2},4)\)

Para los ejercicios 9 - 16, se da la ecuación de una superficie en coordenadas cilíndricas. Encuentra la ecuación de la superficie en coordenadas rectangulares. Identificar y graficar la superficie.

9) [T]\( r=4\)

Responder

Un cilindro de ecuación\( x^2+y^2=16,\) con su centro en el origen y las reglas paralelas al\(z\) eje,

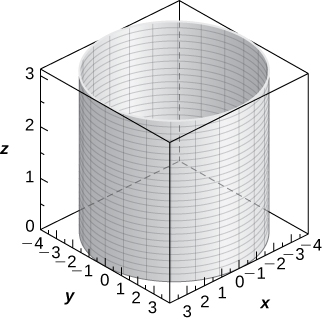
10) [T]\( z=r^2\cos^2θ\)

11) [T]\( r^2\cos(2θ)+z^2+1=0\)

Responder

Hiperboloide de dos hojas de ecuación\( −x^2+y^2−z^2=1,\) con el\(y\) eje -eje como eje de simetría,

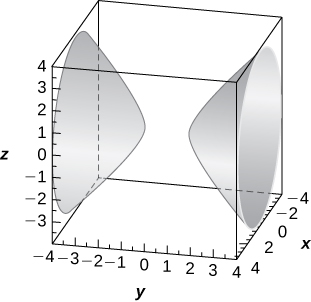
12) [T]\( r=3\sin θ\)

13) [T]\( r=2\cos θ\)

Responder

Cilindro de ecuación\( x^2−2x+y^2=0,\) con un centro en\( (1,0,0)\) y radio\( 1\), con reglas paralelas al\(z\) eje -,

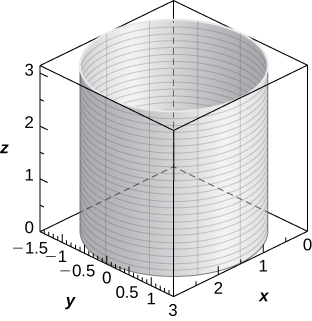
14) [T]\( r^2+z^2=5\)

15) [T]\( r=2\sec θ\)

Responder

Plano de ecuación\( x=2,\)

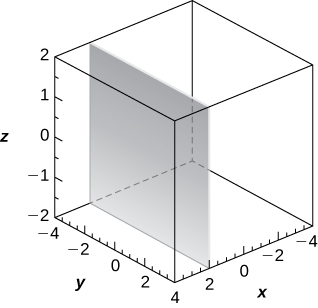
16) [T]\( r=3\csc θ\)

Para los ejercicios 17 - 22, se da la ecuación de una superficie en coordenadas rectangulares. Encuentra la ecuación de la superficie en coordenadas cilíndricas.

17)\( z=3\)

Responder

\( z=3\)

18)\( x=6\)

19)\( x^2+y^2+z^2=9\)

Responder

\( r^2+z^2=9\)

20)\( y=2x^2\)

21)\( x^2+y^2−16x=0\)

Responder

\( r=16\cos θ,\quad r=0\)

22)\( x^2+y^2−3\sqrt{x^2+y^2}+2=0\)

Para los ejercicios 23 - 26, se dan las coordenadas esféricas\( (ρ,θ,φ)\) de un punto. Encuentra las coordenadas rectangulares\( (x,y,z)\) del punto.

23)\( (3,0,π)\)

Responder

\( (0,0,−3)\)

24)\( \left(1,\frac{π}{6},\frac{π}{6}\right)\)

25)\( \left(12,−\frac{π}{4},\frac{π}{4}\right)\)

Responder

\( (6,−6,\sqrt{2})\)

26)\( \left(3,\frac{π}{4},\frac{π}{6}\right)\)

Para los ejercicios 27 - 30, se dan\( (x,y,z)\) las coordenadas rectangulares de un punto. Encuentra las coordenadas esféricas\( (ρ,θ,φ)\) del punto. Exprese la medida de los ángulos en grados redondeados al entero más cercano.

27)\( (4,0,0)\)

Responder

\( (4,0,90°)\)

28)\( (−1,2,1)\)

29)\( (0,3,0)\)

Responder

\( (3,90°,90°)\)

30)\( (−2,2\sqrt{3},4)\)

Para los ejercicios 31 - 36, se da la ecuación de una superficie en coordenadas esféricas. Encuentra la ecuación de la superficie en coordenadas rectangulares. Identificar y graficar la superficie.

31) [T]\( ρ=3\)

Responder

Esfera de ecuación\( x^2+y^2+z^2=9\) centrada en el origen con radio\( 3\),

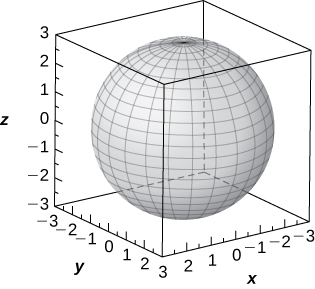
32) [T]\( φ=\frac{π}{3}\)

33) [T]\( ρ=2\cos φ\)

Responder

Esfera de ecuación\( x^2+y^2+(z−1)^2=1\) centrada en\( (0,0,1)\) con radio\( 1\),

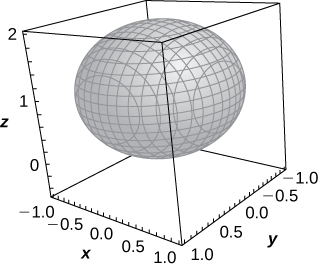
34) [T]\( ρ=4\csc φ\)

35) [T]\( φ=\frac{π}{2}\)

Responder

El\(xy\) -plano de la ecuación\( z=0,\)

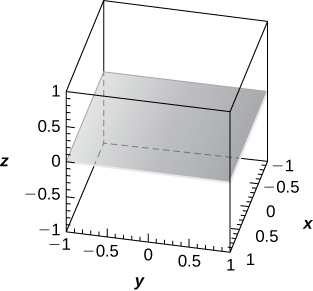
36) [T]\( ρ=6\csc φ\sec θ\)

Para los ejercicios 37 - 40, se da la ecuación de una superficie en coordenadas rectangulares. Encuentra la ecuación de la superficie en coordenadas esféricas. Identificar la superficie.

37)\( x^2+y^2−3z^2=0, \quad z≠0\)

Responder

\( φ=\frac{π}{3}\)o cono\( φ=\frac{2π}{3};\) elíptico

38)\( x^2+y^2+z^2−4z=0\)

39)\( z=6\)

Responder

\( ρ\cos φ=6;\)Avión en\( z=6\)

40)\( x^2+y^2=9\)

Para los ejercicios 41 - 44, se dan las coordenadas cilíndricas de un punto. Encuentra sus coordenadas esféricas asociadas, con la medida del ángulo φ en radianes redondeada a cuatro decimales.

41) [T]\( \left(1,\frac{π}{4},3\right)\)

Responder

\( \left(\sqrt{10},\frac{π}{4},0.3218\right)\)

42) [T]\( (5,π,12)\)

43)\( \left(3,\frac{π}{2},3\right)\)

Responder

\( (3\sqrt{2},\frac{π}{2},\frac{π}{4})\)

44)\( \left(3,−\frac{π}{6},3\right)\)

Para los ejercicios 45 - 48, se dan las coordenadas esféricas de un punto. Encuentra sus coordenadas cilíndricas asociadas.

45)\( \left(2,−\frac{π}{4},\frac{π}{2}\right)\)

Responder

\( \left(2,−\frac{π}{4},0\right)\)

46)\( \left(4,\frac{π}{4},\frac{π}{6}\right)\)

47)\( \left(8,\frac{π}{3},\frac{π}{2}\right)\)

Responder

\( \left(8,\frac{π}{3},0\right)\)

48)\( \left(9,−\frac{π}{6},\frac{π}{3}\right)\)

Para los ejercicios 49 - 52, encuentre el sistema de coordenadas más adecuado para describir los sólidos.

49) El sólido situado en el primer octante con un vértice en el origen y encerrado por un cubo de longitud de borde\( a\), donde\( a>0\)

Responder

Sistema cartesiano,\( \big\{(x,y,z)\,|\,0≤x≤a,\;0≤y≤a,\;0≤z≤a\big\}\)

50) Una concha esférica determinada por la región entre dos esferas concéntricas centradas en el origen, de radios de\( a\) y\( b\), respectivamente, donde\( b>a>0\)

51) Una esfera interior sólida\( x^2+y^2+z^2=9\) y un cilindro exterior\( \left(x−\frac{3}{2}\right)^2+y^2=\frac{9}{4}\)

Responder

Sistema cilíndrico,\( \big\{(r,θ,z)\,|\,r^2+z^2≤9,\;r≥3\cos θ,\;0≤θ≤2π\big\}\)

52) Una cáscara cilíndrica de altura\( 10\) determinada por la región entre dos cilindros con el mismo centro, reglas paralelas, y radios de\( 2\) y\( 5\), respectivamente

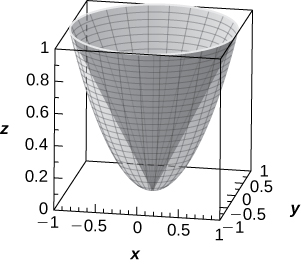
53) [T] Utilice un CAS o CalcPlot3D para graficar en coordenadas cilíndricas la región entre paraboloide elíptico\( z=x^2+y^2\) y cono\( x^2+y^2−z^2=0.\)

Responder

La región es descrita por el conjunto de puntos\( \big\{(r,θ,z)\,|\,0≤r≤1,\;0≤θ≤2π,\;r^2≤z≤r\big\}.\)

54) [T] Utilice un CAS o CalcPlot3D para graficar en coordenadas esféricas la “región del cono de helado” situada por encima del plano XY entre la esfera\( x^2+y^2+z^2=4\) y el cono elíptico\( x^2+y^2−z^2=0.\)

55) Washington, DC, se encuentra en\( 39°\) N y\( 77°\) W (ver la siguiente figura). Supongamos que el radio de la Tierra es\( 4000\) mi. Expresar la ubicación de Washington, DC, en coordenadas esféricas.

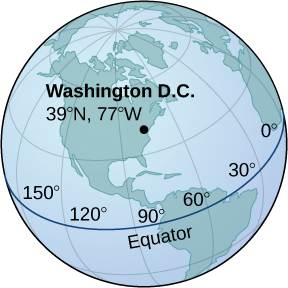
Responder

\( (4000,−77°,51°)\)

56) San Francisco se encuentra en\( 37.78°N\) y\( 122.42°W.\) Asume que el radio de la Tierra es\( 4000\) mi. Expresa la ubicación de San Francisco en coordenadas esféricas.

57) Encuentra la latitud y longitud de Río de Janeiro si sus coordenadas esféricas son\( (4000,−43.17°,102.91°).\)

Responder

\( 43.17°W, 22.91°S\)

58) Encuentra la latitud y longitud de Berlín si sus coordenadas esféricas son\( (4000,13.38°,37.48°).\)

59) [T] Considerar el toro de la ecuación\( \big(x^2+y^2+z^2+R^2−r^2\big)^2=4R^2(x^2+y^2),\) donde\( R≥r>0.\)

a. Escribir la ecuación del toro en coordenadas esféricas.

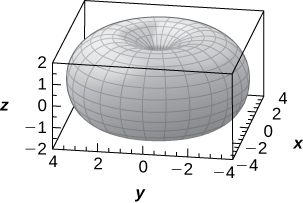
b. Si\( R=r,\) la superficie se llama toro de cuerno. Mostrar que la ecuación de un toro de cuerno en coordenadas esféricas es\( ρ=2R\sin φ.\)

c. Utilice un CAS o CalcPlot3D para graficar el toro de la bocina\( R=r=2\) en coordenadas esféricas.

Responder

a.\(ρ=0, \quad ρ+R^2−r^2−2R\sin φ=0\)

c.

60) [T] La “esfera con baches” con una ecuación en coordenadas esféricas es\( ρ=a+b\cos(mθ)\sin(nφ)\), con\( θ∈[0,2π]\) y\( φ∈[0,π]\), donde\( a\) y\( b\) son números positivos y\( m\) y\( n\) son enteros positivos, puede ser utilizada en matemáticas aplicadas para modelar el crecimiento tumoral.

a. mostrar que la “esfera con baches” está contenida dentro de una esfera de ecuación\( ρ=a+b.\) Encuentra los valores de\( θ\) y\( φ\) en la que se cruzan las dos superficies.

b. Usar un CAS o CalcPlot3D para graficar la superficie para\( a=14, b=2, m=4,\) y\( n=6\) junto con la esfera\( ρ=a+b.\)

c. Encuentra la ecuación de la curva de intersección de la superficie en b. con el cono\( φ=\frac{π}{12}\). Grafique la curva de intersección en el plano de intersección.

Colaboradores

Template:ContribOpenStaxCalc

Enlaces a CalcPlot3D agregados por Paul Seeburger (Monroe Community College).