12.8: Capítulo 12 Ejercicios de revisión
- Page ID
- 116132
Para los ejercicios 1 - 4, determinar si la afirmación es verdadera o falsa. Justificar la respuesta con una prueba o un contraejemplo.
1) Para vectores\(\vecs a\)\(\vecs b\) y y cualquier escalar dado\( c, \, c(\vecs a⋅\vecs b)=(c\vecs a)⋅\vecs b.\)
- Responder
- Cierto; Ver prueba en la Sección 11.3
2) Para vectores\(\vecs a\)\(\vecs b\) y y cualquier escalar dado\( c, \, c(\vecs a×\vecs b)=(c\vecs a)×\vecs b\).
3) La ecuación simétrica para la línea de intersección entre dos planos\( x+y+z=2\) y\( x+2y−4z=5\) viene dada por\( −\frac{x−1}{6}=\frac{y−1}{5}=z.\)
- Responder
- False, convirtiendo las ecuaciones simétricas anteriores a las ecuaciones paramétricas de la línea, obtenemos:
\(x = 1 - 6t\)
\(y = 1 + 5t\)
\(z = t\)
Si esta línea se encuentra en cada plano, deberíamos obtener una identidad (como 5 = 5) cuando sustituir cada expresión de\(t\) en la ecuación de cada plano.
Sustituyendo en la ecuación del primer plano, obtenemos:\( (1-6t) + (1+5t) + t = 2\,\checkmark\)
Así sabemos que esta línea sí se encuentra en el primer plano.
Pero cuando sustituimos en la ecuación del segundo plano, obtenemos:\( (1 - 6t) + 2(1 + 5t) - 4(t) = 1 - 6t + 2 + 10t - 4t = 3 \neq 5\)
Como no obtenemos una identidad, sabemos que esta línea no está en el segundo plano y por lo tanto no puede ser la línea de intersección del dos planos.
4) Si\(\vecs a⋅\vecs b=0,\) entonces\(\vecs a\) es perpendicular a\(\vecs b\).
- Responder
- False, ya que\(\vecs a\) o también\(\vecs b\) podría ser el vector cero.
Para los ejercicios 5 y 6, usa los vectores dados para encontrar las cantidades.
5)\(\vecs a=9\hat{\mathbf{i}}−2\hat{\mathbf{j}},\quad \vecs b=−3\hat{\mathbf{i}}+\hat{\mathbf{k}}\)
a.\( 3\vecs a+\vecs b\)
b.\( \|\vecs a\|\)
c.\(\vecs a×\|\vecs b×\vecs a\|\)
d.\( \|\vecs b×\vecs a\|\)
- Responder
- a.\( ⟨24,−6, 1⟩\)
b.\( \sqrt{85}\)
c. No se puede cruzar un vector con un escalar
d.\( 11\)
6)\(\vecs a=2\hat{\mathbf{i}}+\hat{\mathbf{j}}−9\hat{\mathbf{k}},\quad \vecs b=−\hat{\mathbf{i}}+2\hat{\mathbf{k}},\quad \vecs c=4\hat{\mathbf{i}}−2\hat{\mathbf{j}}+\hat{\mathbf{k}}\)
a.\( 2\vecs a−\vecs b\)
b.\( \|\vecs b×\vecs c\|\)
c.\( \vecs b×\left(\vecs b×\vecs c\right)\)
d.\( \vecs c×\|\vecs b×\vecs a\|\)
e.\( \text{Proj}_\vecs{a}\vecs b\)
7) Encontrar los valores de\(a\) tal que los vectores\( ⟨2,4,a⟩\) y\( ⟨0,−1,a⟩\) son ortogonales.
- Responder
- \( a=±2\)
Para los ejercicios 8 y 9, encuentra los vectores unitarios.
8) Encuentra el vector unitario que tiene la misma dirección que el vector\(\vecs v\) que comienza en\( (0,−3)\) y termina en\( (4,10).\)
9) Encuentra el vector unitario que tiene la misma dirección que el vector\(\vecs v\) que comienza en\( (1,4,10)\) y termina en\( (3,0,4).\)
- Responder
- \( ⟨\frac{1}{\sqrt{14}},−\frac{2}{\sqrt{14}},−\frac{3}{\sqrt{14}}⟩ = ⟨\frac{\sqrt{14}}{14},−\frac{\sqrt{14}}{7},−\frac{3\sqrt{14}}{14}⟩ \)
Para los ejercicios 10 y 11, encuentra el área o volumen de las formas dadas.
10) El paralelogramo abarcado por vectores\(\vecs a=⟨1,13⟩\) y\(\vecs b=⟨3,21⟩\)
11) El paralelepípedo formado por\(\vecs a=⟨1,4,1⟩\) y\(\vecs b=⟨3,6,2⟩,\) y\(\vecs c=⟨−2,1,−5⟩\)
- Responder
- \( 27\)unidades\(^2\)
Para los ejercicios 12 y 13, encuentra las ecuaciones paramétricas y la ecuación vectorial de la línea con las propiedades dadas.
12) La línea que pasa por el punto\( (2,−3,7)\) que es paralelo al vector\( ⟨1,3,−2⟩\)
13) La línea que pasa por puntos\( (1,3,5)\) y\( (−2,6,−3)\)
- Responder
- \( x=1−3t,y=3+3t,z=5−8t,\quad \vecs r(t)=(1−3t)\hat{\mathbf{i}}+3(1+t)\hat{\mathbf{j}}+(5−8t)\hat{\mathbf{k}}\)
Para los ejercicios 14 y 15, encuentra la ecuación del plano con las propiedades dadas.
14) El plano que pasa por el punto\( (4,7,−1)\) y tiene vector normal\(\vecs n=⟨3,4,2⟩\)
15) El plano que pasa por puntos\( (0,1,5),(2,−1,6),\) y\( (3,2,5).\)
- Responder
- \( −x+3y+8z=43\)
Para los ejercicios 16 y 17, encuentra las trazas para las superficies en planos\( x=k,y=k\), y\( z=k.\) luego, describe y dibuja las superficies.
16)\( 9x^2+4y^2−16y+36z^2=20\)
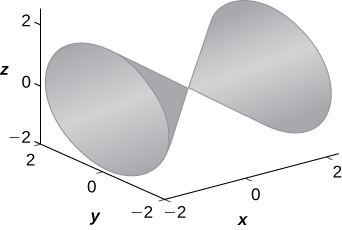
17)\( x^2=y^2+z^2\)
- Responder
- \( x=k\)trace:\( k^2=y^2+z^2\) es un círculo,\( y=k\) trace:\( x^2−z^2=k^2\) es una hipérbola (o un par de líneas si\( k=0), z=k\) trace:\( x^2−y^2=k^2\) es una hipérbola (o un par de líneas si\( k=0\)). La superficie es un cono.
Para los ejercicios 18 y 19, escriba la ecuación dada en coordenadas cilíndricas y coordenadas esféricas.
18)\( x^2+y^2+z^2=144\)
19)\( z=x^2+y^2−1\)
- Responder
- Cilíndrica:\( z=r^2−1,\) esférica\( \cos φ=ρ\sin^2 φ−\frac{1}{ρ}\)
Para los ejercicios 20 y 21, convierta las ecuaciones dadas de coordenadas cilíndricas o esféricas a coordenadas rectangulares. Identificar la superficie dada.
20)\( ρ^2(\sin^2(φ)−\cos^2(φ))=1\)
21)\( r^2−2r\cos(θ)+z^2=1\)
- Responder
- \( x^2−2x+y^2+z^2=1\), esfera
Para los ejercicios 22 y 23, considera un bote pequeño que cruza un río.
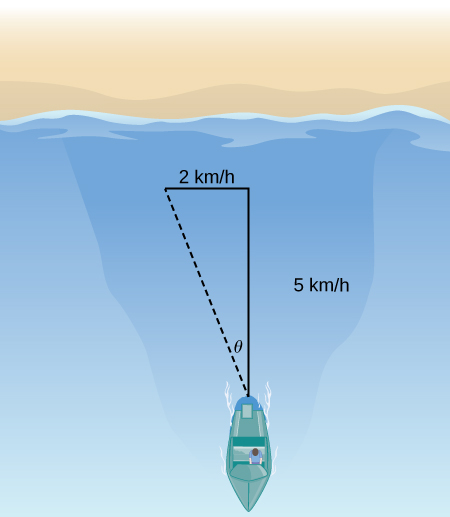
22) Si la velocidad de la embarcación es\( 5\) km/h hacia el norte en aguas tranquilas y el agua tiene una corriente de\( 2\) km/h con respecto al oeste (ver la siguiente figura), ¿cuál es la velocidad de la embarcación relativa a la orilla? ¿Cuál es el ángulo por el\( θ\) que está viajando realmente el barco?
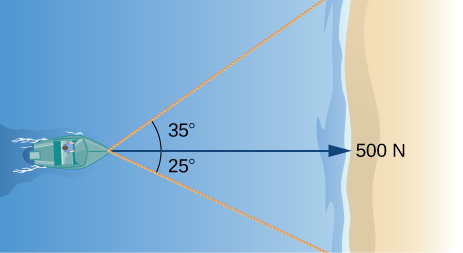
23) Cuando la embarcación llega a la orilla, se lanzan dos cuerdas a la gente para ayudar a tirar del bote a tierra. Una cuerda está en un ángulo de\( 25°\) y la otra está en\( 35°\). Si la embarcación debe ser jalada recta y con una fuerza de\( 500\) N, encuentre la magnitud de la fuerza para cada cuerda (ver la siguiente figura).
- Responder
- 331 N y 244 N
24) Un avión vuela en dirección a 52° este de norte con una velocidad de 450 mph. Un viento fuerte tiene un rumbo 33° al este del norte con una velocidad de 50 mph. ¿Cuál es la velocidad de avance resultante y el rumbo del avión?
25) Calcular el trabajo realizado moviendo una partícula de posición\( (1,2,0)\) a\( (8,4,5)\) lo largo de una línea recta con una fuerza\(\vecs F=2\hat{\mathbf{i}}+3\hat{\mathbf{j}}−\hat{\mathbf{k}}.\)
- Responder
- \( 15\)J
En los problemas 26 y 27, considere su intento fallido de quitar la llanta de su automóvil usando una llave para aflojar los tornillos. Suponga que la llave es de\( 0.3\) m de largo y puede aplicar una fuerza de 200-N.
26) Debido a que tu llanta está desplana, solo puedes aplicar tu fuerza en\( 60°\) ángulo. ¿Cuál es el par en el centro del perno? Supongamos que esta fuerza no es suficiente para aflojar el perno.
27) Alguien te presta un gato de llantas y ahora puedes aplicar una fuerza de 200-N en\( 80°\) ángulo. ¿Su par resultante va a ser más o menos? ¿Cuál es el nuevo par resultante en el centro del perno? Supongamos que esta fuerza no es suficiente para aflojar el perno.
- Responder
- Más,\( 59.09\) J