14.6: Derivadas direccionales y el gradiente

Objetivos de aprendizaje

• Determinar la derivada direccional en una dirección dada para una función de dos variables.
• Determinar el vector de gradiente de una función de valor real dada.
• Explicar la importancia del vector de gradiente con respecto a la dirección de cambio a lo largo de una superficie.
• Usa el degradado para encontrar la tangente a una curva de nivel de una función dada.
• Calcular derivadas direccionales y gradientes en tres dimensiones.

Una función\(z=f(x,y)\) tiene dos derivadas parciales:\(∂z/∂x\) y\(∂z/∂y\). Estas derivadas corresponden a cada una de las variables independientes y pueden interpretarse como tasas de cambio instantáneas (es decir, como pendientes de una línea tangente). Por ejemplo,\(∂z/∂x\) representa la pendiente de una línea tangente que pasa por un punto dado en la superficie definida\(z=f(x,y),\) asumiendo que la línea tangente es paralela al \(x\)eje -eje. Del mismo modo,\(∂z/∂y\) representa la pendiente de la línea tangente paralela al \(y\)eje -eje. Ahora consideramos la posibilidad de una línea tangente paralela a ninguno de los ejes.

Derivados direccionales

Comenzamos con la gráfica de una superficie definida por la ecuación\(z=f(x,y)\). Dado un punto\((a,b)\) en el dominio de\(f\), elegimos una dirección para viajar desde ese punto. Medimos la dirección usando un ángulo\(θ\), que se mide en sentido antihorario en el\(xy\) plano, comenzando en cero desde el\(x\) eje positivo (Figura\(\PageIndex{1}\)). La distancia que recorremos es\(h\) y la dirección que viajamos viene dada por el vector unitario\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}.\) Por lo tanto, la\(z\) coordenada -del segundo punto en la gráfica viene dada por\(z=f(a+h\cos θ,b+h\sin θ).\)

Figura\(\PageIndex{1}\): Encontrar la derivada direccional en un punto de la gráfica de\(z=f(x,y)\). La pendiente de la flecha azul en la gráfica indica el valor de la derivada direccional en ese punto.

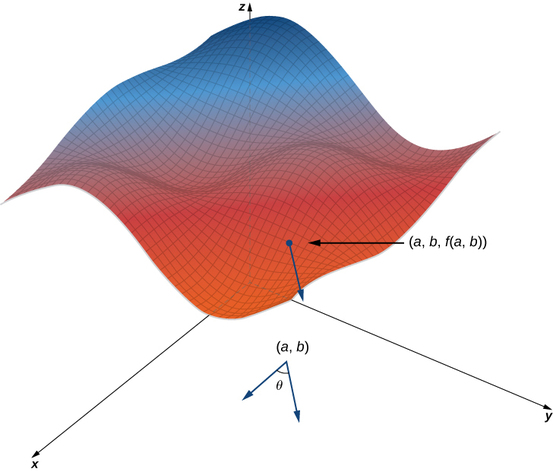
Podemos calcular la pendiente de la línea secante dividiendo la diferencia en\(z\) -valores por la longitud del segmento de línea que conecta los dos puntos en el dominio. La longitud del segmento de línea es\(h\). Por lo tanto, la pendiente de la línea secante es

\[m_{sec}=\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \]

Para encontrar la pendiente de la línea tangente en la misma dirección, tomamos el límite a medida que se\(h\) acerca a cero.

Definición: Derivados direccionales

Supongamos que\(z=f(x,y)\) es una función de dos variables con un dominio de\(D\). Dejar\((a,b)∈D\) y definir\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\). Entonces la derivada direccional de\(f\) en la dirección de\(\vecs u\) viene dada por

\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h \cos θ,b+h\sin θ)−f(a,b)}{h} \label{DD} \]

siempre que exista el límite.

La ecuación\ ref {DD} proporciona una definición formal de la derivada direccional que se puede usar en muchos casos para calcular una derivada direccional.

Tenga en cuenta que dado que el punto\((a, b)\) se elige aleatoriamente\(D\) del dominio de la función\(f\), podemos usar esta definición para encontrar la derivada direccional en función de\(x\) y\(y\).

Es decir,

\[D_{\vecs u}f(x,y)=\lim_{h→0}\dfrac{f(x+h \cos θ,y+h\sin θ)−f(x,y)}{h} \label{DDxy} \]

Ejemplo\(\PageIndex{1}\): Finding a Directional Derivative from the Definition

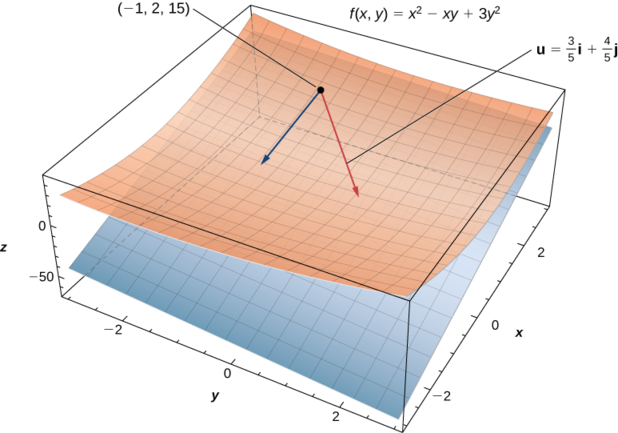
Vamos\(θ=\arccos(3/5).\) Encuentra la derivada direccional\(D_{\vecs u}f(x,y)\) de\(f(x,y)=x^2−xy+3y^2\) en la dirección de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\).

Después determinar\(D_{\vecs u}f(−1,2)\).

Solución

En primer lugar, ya que\(\cos θ=3/5\) y\(θ\) es agudo, esto implica

\[\sin θ=\sqrt{1−\left(\dfrac{3}{5}\right)^2}=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}. \nonumber \]

Usando primero\(f(x,y)=x^2−xy+3y^2,\) calculamos\(f(x+h\cos θ,y+h\sin θ)\):

\ [\ begin {alinear*} f (x+h\ cos θ, y+h\ sin θ) &= (x+h\ cos θ) ^2− (x+h\ cos θ) (y+h\ sin θ) +3 (y+h\ sin θ) ^2\\
&=x^2+2xh\ cos θ+h^2\ cos^2 θ−xy−xh\ sin θ−yh\ cos θ−h^2\ sin θ\ cos θ+3y^2+6yh\ sin θ+3h^2\ sen ^2 θ\
&=x^2+2xh (\ frac {3} {5}) +\ frac {9h^2} {25} −xy−\ frac {4xh} {5} −\ frac {3yh} {5} −\ frac {12h ^2} {25} +3y^2+6yh (\ frac {4} {5}) +3h^2 (\ frac {16} {25})\\
&=x^2−xy+3y^2+\ frac {2xh} {5} +\ frac {9h^2} {5} +\ frac {21yh} {5}. \ end {alinear*}\]

Sustituimos esta expresión en Ecuación\ ref {DD} con\(a = x\) y\(b = y\):

\ [\ begin {alinear*} D_ {\ vecs u} f (x, y) &=\ lim_ {h→0}\ frac {f (x+h\ cos θ, y+h\ sin θ) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ frac {(x^2−xy+3y^2+\ frac {2xh} {5} +\ frac {9h^2} {5} +\ frac {21yh} {5}) − (x^2−xy+3y^2)} {h}\\
&=\ lim_ {h→0}\ frac {\ frac {2xh} {5} +\ frac {9h^2} {5} +\ frac {21h} yh} {5}} {h}\\
& ; =\ lim_ {h→0}\ frac {2x} {5} +\ frac {9h} {5} +\ frac {21y} {5}\\
&=\ frac {2x+21y} {5}. \ end {alinear*}\]

Para calcular\(D_{\vecs u}f(−1,2),\) sustituimos\(x=−1\) y\(y=2\) en esta respuesta (Figura\(\PageIndex{2}\)):

\[ D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8. \nonumber \]

Figura\(\PageIndex{2}\): Encontrar la derivada direccional en una dirección dada\(\vecs u\) en un punto dado en una superficie. El plano es tangente a la superficie en el punto dado\((−1,2,15).\)

En el siguiente teorema se esboza un enfoque más fácil para calcular derivadas direccionales que involucran derivadas parciales.

Derivada direccional de una función de dos variables

Dejar\(z=f(x,y)\) ser una función de dos variables\(x\) y\(y\), y asumir que\(f_x\) y\(f_y\) existir. Entonces la derivada direccional de\(f\) en la dirección de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\) viene dada por

\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \label{DD2v} \]

Prueba

Aplicando la definición de una derivada direccional indicada anteriormente en la Ecuación\ ref {DD}, se\(f\) puede escribir la derivada direccional de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\) en la dirección de\((x_0, y_0)\) en un punto en el dominio de\(f\)

\[D_{\vecs u}f((x_0, y_0))=\lim_{t→0}\dfrac{f(x_0+t \cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]

Dejar\(x=x_0+t\cos θ\)\(y=y_0+t\sin θ,\) y definir\(g(t)=f(x,y)\). Ya que\(f_x\) y\(f_y\) ambos existen, podemos usar la regla de cadena para funciones de dos variables para calcular\(g′(t)\):

\[g′(t)=\dfrac{∂f}{∂x}\dfrac{dx}{dt}+\dfrac{∂f}{∂y}\dfrac{dy}{dt}=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]

Si\(t=0,\) entonces\(x=x_0\) y\(y=y_0,\) así

\[g′(0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ \nonumber \]

Por la definición de\(g′(t),\) ello también es cierto que

\[g′(0)=\lim_{t→0}\dfrac{g(t)−g(0)}{t}=\lim_{t→0}\dfrac{f(x_0+t\cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]

Por lo tanto,\(D_{\vecs u}f(x_0,y_0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ\).

Dado que el punto\( (x_0,y_0) \) es un punto arbitrario del dominio de\(f\), este resultado se sostiene para todos los puntos en el dominio de\(f\) para los que\(f_y\) existen\(f_x\) y parciales.

Por lo tanto,\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]

□

Ejemplo\(\PageIndex{2}\): Finding a Directional Derivative: Alternative Method

Vamos\(θ=\arccos (3/5).\) Encuentra la derivada direccional\(D_{\vecs u}f(x,y)\) de\(f(x,y)=x^2−xy+3y^2\) en la dirección de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\).

Después determinar\(D_{\vecs u}f(−1,2)\).

Solución

Primero, debemos calcular las derivadas parciales de\(f\):

\[\begin{align*}f_x(x,y) &=2x−y \\ f_y(x,y) &=−x+6y, \end{align*}\]

Luego usamos la ecuación\ ref {dd2v} con\(θ=\arccos (3/5)\):

\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y)\ cos θ+f_y (x, y)\ sin θ\
& =( 2x−y)\ dfrac {3} {5} + (−x+6y)\ dfrac {4} {5}\\
&=\ dfrac {6x} {5} −\ dfrac {3y} {5} −\ dfrac {4x} {5} +\ dfrac {24y} {5}\\
&=\ dfrac {2x+21y} {5}. \ end {alinear*}\]

Para calcular\(D_{\vecs u}f(−1,2),\) let\(x=−1\) y\(y=2\):

\[D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8.\nonumber \]

Esta es la misma respuesta obtenida en Ejemplo\(\PageIndex{1}\).

Ejercicio\(\PageIndex{1}\):

Encuentra la derivada direccional\(D_{\vecs u}f(x,y)\) de\(f(x,y)=3x^2y−4xy^3+3y^2−4x\) en la dirección de\(\vecs u=(\cos \dfrac{π}{3})\,\hat{\mathbf i}+(\sin \dfrac{π}{3})\,\hat{\mathbf j}\) usar la ecuación\ ref {dd2v}.

¿Qué es\(D_{\vecs u} f(3,4)\)?

Pista

Calcular las derivadas parciales y determinar el valor de\(θ\).

Contestar

\(D_{\vecs u}f(x,y)=\dfrac{(6xy−4y^3−4)(1)}{2}+\dfrac{(3x^2−12xy^2+6y)\sqrt{3}}{2}\)

\(D_{\vecs u}f(3,4)=\dfrac{72−256−4}{2}+\dfrac{(27−576+24)\sqrt{3}}{2}=−94−\dfrac{525\sqrt{3}}{2}\)

Si el vector que se da para la dirección de la derivada no es un vector unitario, entonces solo es necesario dividirlo por la norma del vector. Por ejemplo, si quisiéramos encontrar la derivada direccional de la función en Ejemplo\(\PageIndex{2}\) en la dirección del vector\(⟨−5,12⟩\), primero dividiríamos por su magnitud para obtener\(\vecs u\). Esto nos da\(\vecs u=⟨−\frac{5}{13},\frac{12}{13}⟩\).

Entonces

\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y)\ cos θ+f_y (x, y)\ sin θ\
&=−\ dfrac {5} {13} (2x−y) +\ dfrac {12} {13} (−x+6y)\\
&=−\ dfrac {22} {13} x+\ dfrac {17} {13} y\ final {alinear*}\]

Gradiente

El lado derecho de la Ecuación\ ref {dd2v} es igual a\(f_x(x,y)\cos θ+f_y(x,y)\sin θ\), que se puede escribir como el producto de punto de dos vectores. Definir el primer vector como\(\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\) y el segundo vector como\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\). Entonces el lado derecho de la ecuación se puede escribir como el producto de puntos de estos dos vectores:

\[D_{\vecs u}f(x,y)=\vecs ∇f(x,y)⋅\vecs u. \label{gradDirDer} \]

El primer vector en Ecuación\ ref {gradDirder} tiene un nombre especial: el gradiente de la función\(f\). El símbolo\(∇\) se llama nabla y el vector\(\vecs ∇f\) se lee “del”\(f\).

Definición: El gradiente

Que\(z=f(x,y)\) sea una función de\(x\) y\(y\) tal que\(f_x\) y\(f_y\) exista. El vector\(\vecs ∇f(x,y)\) se llama el gradiente de\(f\) y se define como

\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}. \label{grad} \]

El vector también\(\vecs ∇f(x,y)\) se escribe como “grad\(f\).”

Ejemplo\(\PageIndex{3}\): Finding Gradients

Encuentra el gradiente\(\vecs ∇f(x,y)\) de cada una de las siguientes funciones:

1. \(f(x,y)=x^2−xy+3y^2\)
2. \(f(x,y)=\sin 3 x \cos 3y\)

Solución

Para ambas partes a. y b., primero calculamos las derivadas parciales\(f_x\) y\(f_y\), luego, usamos la Ecuación\ ref {grad}.

a.\( f_x(x,y)=2x−y\) y\(f_y(x,y)=−x+6y\), entonces

\[\begin{align*} \vecs ∇f(x,y) &=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\\ &=(2x−y)\,\hat{\mathbf i}+(−x+6y)\,\hat{\mathbf j}.\end{align*}\]

b.\( f_x(x,y)=3\cos 3x \cos 3y\) y\(f_y(x,y)=−3\sin 3x \sin 3y\), entonces

\ [\ begin {align*}\ vecs f (x, y) &=f_x (x, y)\,\ hat {\ mathbf i} +f_y (x, y)\,\ hat {\ mathbf j}\\
& =( 3\ cos 3x\ cos 3y)\,\ hat {\ mathbf i} − (3\ sin 3x\ sin 3y)\,\ hat {\ mathbf j}. \ end {alinear*}\]

Ejercicio\(\PageIndex{2}\)

Encuentra el gradiente\(\vecs ∇f(x,y)\) de\(f(x,y)=\dfrac{x^2−3y^2}{2x+y}\).

Pista

Calcula las derivadas parciales, luego usa la Ecuación\ ref {grad}.

Contestar

\(\vecs ∇f(x,y)=\dfrac{2x^2+2xy+6y^2}{(2x+y)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2}{(2x+y)^2}\,\hat{\mathbf j}\)

El gradiente tiene algunas propiedades importantes. Ya hemos visto una fórmula que usa el gradiente: la fórmula para la derivada direccional. Recordemos de The Dot Product que si el ángulo entre dos vectores\(\vecs a\) y\(\vecs b\) es\(φ\), entonces\(\vecs a⋅\vecs b=‖\vecs a‖‖\vecs b‖\cos φ.\) Por lo tanto, si el ángulo entre\(\vecs ∇f(x_0,y_0)\) y\(\vecs u=(cosθ)\,\hat{\mathbf i}+(sinθ)\,\hat{\mathbf j}\) es\(φ\), tenemos

\[D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=\|\vecs ∇f(x_0,y_0)\|‖\vecs u‖\cos φ=\|\vecs ∇f(x_0,y_0)\|\cos φ. \nonumber \]

El\(‖\vecs u‖\) desaparece porque\(\vecs u\) es un vector unitario. Por lo tanto, la derivada direccional es igual a la magnitud del gradiente evaluado a\((x_0,y_0)\) multiplicado por\(\cos φ\). Recordemos que\(\cos φ\) va desde\(−1\) hasta\(1\).

Si\(φ=0,\) entonces\(\cos φ=1\) y\(\vecs ∇f(x_0,y_0)\) y\(\vecs u\) ambos apuntan en la misma dirección.

Si\(φ=π\), entonces\(\cos φ=−1\) y\(\vecs ∇f(x_0,y_0)\) y\(\vecs u\) apuntar en direcciones opuestas.

En el primer caso,\(D_{\vecs u}f(x_0,y_0)\) se maximiza el valor de; en el segundo caso,\(D_{\vecs u}f(x_0,y_0)\) se minimiza el valor de.

También podemos ver que si\(\vecs ∇f(x_0,y_0)=\vecs 0\), entonces

\[ D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=0 \nonumber \]

para cualquier vector\(\vecs u\). Estos tres casos se describen en el siguiente teorema.

Propiedades del Degradado

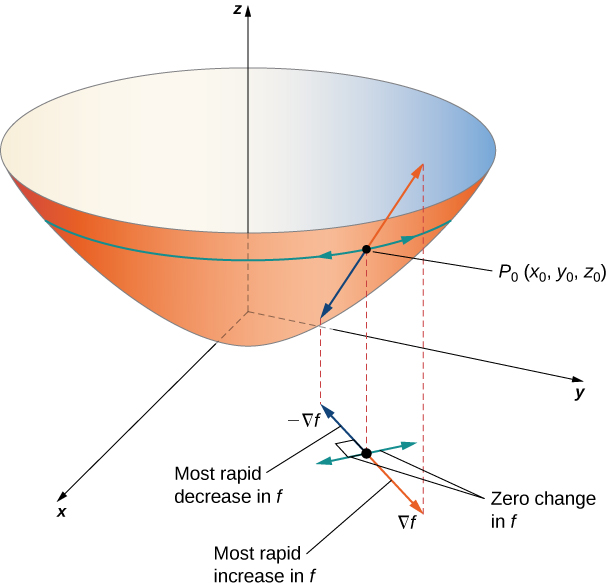
Supongamos que la función\(z=f(x,y)\) es diferenciable en\((x_0,y_0)\) (Figura\(\PageIndex{3}\)).

1. Si\(\vecs ∇f(x_0,y_0)=\vecs 0\), entonces\(D_{\vecs u}f(x_0,y_0)=0\) para cualquier vector de unidad\(\vecs u\).
2. Si\(\vecs ∇f(x_0,y_0)≠ \vecs 0\), entonces\(D_{\vecs u}f(x_0,y_0)\) se maximiza cuando\(\vecs u\) apunta en la misma dirección que\(\vecs ∇f(x_0,y_0)\). El valor máximo de\(D_{\vecs u}f(x_0,y_0)\) es\(\|\vecs ∇f(x_0,y_0)\|\).
3. Si\(\vecs ∇f(x_0,y_0)≠\vecs 0\), entonces\(D_{\vecs u}f(x_0,y_0)\) se minimiza cuando\(\vecs u\) apunta en la dirección opuesta a\(\vecs ∇f(x_0,y_0)\). El valor mínimo de\(D_{\vecs u}f(x_0,y_0)\) es\(−\|\vecs ∇f(x_0,y_0)\|\).

Figura\(\PageIndex{3}\): El gradiente indica los valores máximo y mínimo de la derivada direccional en un punto.

Ejemplo\(\PageIndex{4}\): Finding a Maximum Directional Derivative

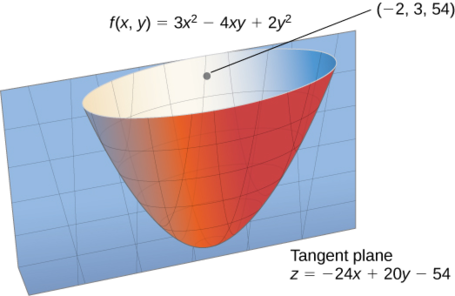
Encuentra la dirección para la cual la derivada direccional de\(f(x,y)=3x^2−4xy+2y^2\) at\((−2,3)\) es máxima. ¿Cuál es el valor máximo?

Solución

El valor máximo de la derivada direccional ocurre cuando\(\vecs ∇f\) y el punto de vector unitario en la misma dirección. Por lo tanto, comenzamos calculando\(\vecs ∇f(x,y\)):

\[f_x(x,y)=6x−4y \; \text{and}\; f_y(x,y)=−4x+4y \nonumber \]

entonces

\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}=(6x−4y)\,\hat{\mathbf i}+(−4x+4y)\,\hat{\mathbf j}. \nonumber \]

A continuación, evaluamos el gradiente en\((−2,3)\):

\[\vecs ∇f(−2,3)=(6(−2)−4(3))\,\hat{\mathbf i}+(−4(−2)+4(3))\,\hat{\mathbf j}=−24\,\hat{\mathbf i}+20\,\hat{\mathbf j}. \nonumber \]

Necesitamos encontrar un vector unitario que apunte en la misma dirección\(\vecs ∇f(−2,3),\) así el siguiente paso es dividir\(\vecs ∇f(−2,3)\) por su magnitud, que es\(\sqrt{(−24)^2+(20)^2}=\sqrt{976}=4\sqrt{61}\). Por lo tanto,

\[\dfrac{\vecs ∇f(−2,3)}{\|\vecs ∇f(−2,3)\|}=\dfrac{−24}{4\sqrt{61}}i+\dfrac{20}{4\sqrt{61}}j=−\dfrac{6\sqrt{61}}{61}\,\hat{\mathbf i}+\dfrac{5\sqrt{61}}{61}\,\hat{\mathbf j}. \nonumber \]

Este es el vector unitario que apunta en la misma dirección que\(\vecs ∇f(−2,3).\) Para encontrar el ángulo correspondiente a este vector unitario, resolvemos las ecuaciones

\[\cos θ=\dfrac{−6\sqrt{61}}{61}\; \text{and}\; \sin θ=\dfrac{5\sqrt{61}}{61} \nonumber \]

para\(θ\). Dado que el coseno es negativo y el seno es positivo, el ángulo debe estar en el segundo cuadrante. Por lo tanto,\(θ=π−\arcsin((5\sqrt{61})/61)≈2.45\) rad.

El valor máximo de la derivada direccional at\((−2,3)\) es\(\|\vecs ∇f(−2,3)\|=4\sqrt{61}\) (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): El valor máximo de la derivada direccional at\((−2,3)\) está en la dirección del gradiente.

Ejercicio\(\PageIndex{3}\)

Encuentra la dirección para la cual la derivada direccional de\(g(x,y)=4x−xy+2y^2\) at\((−2,3)\) es máxima. ¿Cuál es el valor máximo?

Pista

Evaluar el gradiente de\(g\) en punto\((−2,3)\).

Contestar

El gradiente de\(g\) at\((−2,3)\) es\(\vecs ∇g(−2,3)=\,\hat{\mathbf i}+14\,\hat{\mathbf j}\). El vector unitario que apunta en la misma dirección que\(\vecs ∇g(−2,3)\) es

\[\dfrac{\vecs ∇g(−2,3)}{\|\vecs ∇g(−2,3)\|}=\dfrac{1}{\sqrt{197}}\,\hat{\mathbf i}+\dfrac{14}{\sqrt{197}}\,\hat{\mathbf j}=\dfrac{\sqrt{197}}{197}\,\hat{\mathbf i}+\dfrac{14\sqrt{197}}{197}\,\hat{\mathbf j},\nonumber \]

lo que da un ángulo de\(θ=\arcsin ((14\sqrt{197})/197)≈1.499\) rad.

El valor máximo de la derivada direccional es\(\|\vecs ∇g(−2,3)\|=\sqrt{197}\).

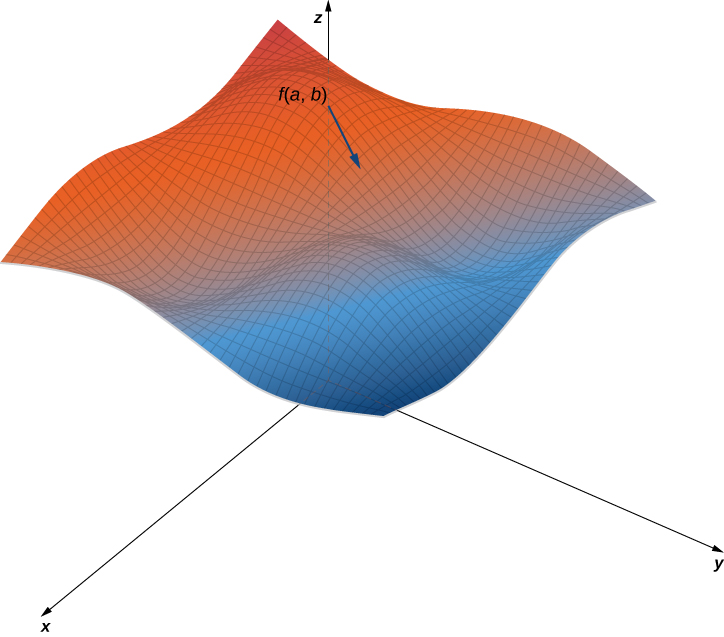
La figura\(\PageIndex{5}\) muestra una porción de la gráfica de la función\(f(x,y)=3+\sin x \sin y\). Dado un punto\((a,b)\) en el dominio de\(f\), el valor máximo de la derivada direccional en ese punto viene dado por\(\|\vecs ∇f(a,b)\|\). Esto equivaldría a la tasa de mayor ascenso si la superficie representara un mapa topográfico. Si fuéramos en sentido contrario, sería la tasa de mayor descenso.

Figura\(\PageIndex{5}\): Una superficie típica en\(\mathbb R^3\). Dado un punto en la superficie, la derivada direccional se puede calcular usando el gradiente.

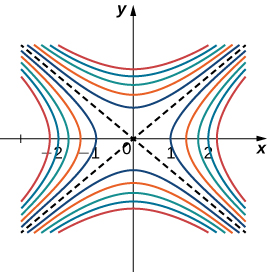
Cuando se utiliza un mapa topográfico, la pendiente más pronunciada siempre está en la dirección donde las curvas de nivel están más próximas entre sí (Figura\(\PageIndex{6}\)). Esto es análogo al mapa de contorno de una función, asumiendo que las curvas de nivel se obtienen para valores igualmente espaciados en todo el rango de esa función.

Figura\(\PageIndex{6}\): Mapa de contorno para la función\(f(x,y)=x^2−y^2\) usando valores de nivel entre\(−5\) y\(5\).

Gradientes y curvas de nivel

Recordemos que si una curva es definida paramétricamente por el par de funciones\((x(t),y(t)),\) entonces el vector\(x′(t)\,\hat{\mathbf i}+y′(t)\,\hat{\mathbf j}\) es tangente a la curva para cada valor de\(t\) en el dominio. Ahora supongamos que\(z=f(x,y)\) es una función diferenciable de\(x\) y\(y\), y\((x_0,y_0)\) está en su dominio. Supongamos además eso\(x_0=x(t_0)\) y\(y_0=y(t_0)\) por algún valor de\(t\), y consideremos la curva de nivel\(f(x,y)=k\). Definir\(g(t)=f(x(t),y(t))\) y calcular\(g′(t)\) en la curva de nivel. Por la cadena Regla,

\[g′(t)=f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t). \nonumber \]

Pero\(g′(t)=0\) porque\(g(t)=k\) para todos\(t\). Por lo tanto, por una parte,

\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=0; \nonumber \]

por otra parte,

\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩. \nonumber \]

Por lo tanto,

\[\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩=0. \nonumber \]

Así, el producto punto de estos vectores es igual a cero, lo que implica que son ortogonales. Sin embargo, el segundo vector es tangente a la curva de nivel, lo que implica que el gradiente debe ser normal a la curva de nivel, lo que da lugar al siguiente teorema.

El gradiente es normal a la curva de nivel

Supongamos que la función\(z=f(x,y)\) tiene derivadas parciales continuas de primer orden en un disco abierto centrado en un punto\((x_0,y_0)\). Si\(\vecs ∇f(x_0,y_0)≠0\), entonces\(\vecs ∇f(x_0,y_0)\) es normal a la curva de nivel de\(f\) at\((x_0,y_0).\)

Podemos utilizar este teorema para encontrar vectores tangentes y normales para nivelar curvas de una función.

Ejemplo\(\PageIndex{5}\): Finding Tangents to Level Curves

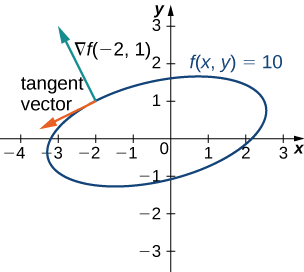
Para la función\(f(x,y)=2x^2−3xy+8y^2+2x−4y+4,\) encontrar un vector tangente a la curva de nivel en el punto\((−2,1)\). Grafica la curva de nivel correspondiente\(f(x,y)=18\) y dibuja\(\vecs ∇f(−2,1)\) y un vector tangente.

Solución

Primero, debemos calcular\(\vecs ∇f(x,y):\)

\[f_x(x,y)=4x−3y+2 \;\text{and}\; f_y=−3x+16y−4 \;\text{so}\; \vecs ∇f(x,y)=(4x−3y+2)\,\hat{\mathbf i}+(−3x+16y−4)\,\hat{\mathbf j}.\nonumber \]

A continuación, evaluamos\(\vecs ∇f(x,y)\) en\((−2,1):\)

\[\vecs ∇f(−2,1)=(4(−2)−3(1)+2)\,\hat{\mathbf i}+(−3(−2)+16(1)−4)\,\hat{\mathbf j}=−9\,\hat{\mathbf i}+18\,\hat{\mathbf j}.\nonumber \]

Este vector es ortogonal a la curva en el punto\((−2,1)\). Podemos obtener un vector tangente invirtiendo los componentes y multiplicando cualquiera de ellos por\(−1\). Así, por ejemplo,\(−18\,\hat{\mathbf i}−9\,\hat{\mathbf j}\) es un vector tangente (Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\): Vectores tangentes y normales\(2x^2−3xy+8y^2+2x−4y+4=18\) a punto\((−2,1)\).

Ejercicio\(\PageIndex{4}\)

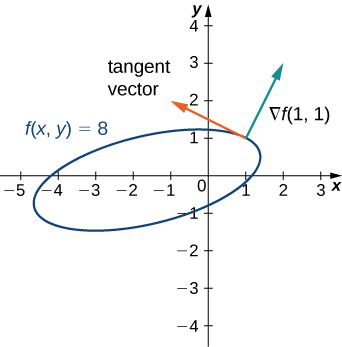
Para la función\(f(x,y)=x^2−2xy+5y^2+3x−2y+3\), encuentra la tangente a la curva de nivel en el punto\((1,1)\). Dibuja la gráfica de la curva de nivel correspondiente\(f(x,y)=8\) y dibuja\(\vecs ∇f(1,1)\) y un vector tangente.

Pista

Calcular el gradiente en el punto\((1,1)\).

Contestar

\(\vecs ∇f(x,y)=(2x−2y+3)\,\hat{\mathbf i}+(−2x+10y−2)\,\hat{\mathbf j}\)

\(\vecs ∇f(1,1)=3\,\hat{\mathbf i}+6\,\hat{\mathbf j}\)

Vector tangente:\(6\,\hat{\mathbf i}−3\,\hat{\mathbf j}\) o\(−6\,\hat{\mathbf i}+3\,\hat{\mathbf j}\)

Gradientes tridimensionales y derivados direccionales

La definición de un gradiente puede extenderse a funciones de más de dos variables.

Definición: Gradientes en 3D

Dejar\(w=f(x, y, z)\) ser una función de tres variables tales que\(f_x, \, f_y\),fx,fy,andfzfx,fy,andfz" role="presentation" tabindex="0"> y\(f_z\) existir. El vector\(\vecs ∇f(x,y,z)\) se llama el gradiente deff" role="presentation" tabindex="0">\(f\) y se define como

\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}.\label{grad3d} \]

\(\vecs ∇f(x,y,z)\)también se puede escribir como grad\(f(x,y,z).\)

Calcular el gradiente de una función en tres variables es muy similar a calcular el gradiente de una función en dos variables. Primero, calculamos las derivadas parciales\(f_x, \, f_y,\) y\(f_z\), y luego usamos la Ecuación\ ref {grad3d}.

Ejemplo\(\PageIndex{6}\): Finding Gradients in Three Dimensions

Encuentra el gradiente\(\vecs ∇f(x,y,z)\) de cada una de las siguientes funciones:

1. \(f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz\)
2. \(f(x,y,z)=e^{−2z}\sin 2x \cos 2y\)

Solución

Para ambas partes a. y b., primero calculamos las derivadas parciales\(f_x,f_y,\) y\(f_z\), luego, usamos la Ecuación\ ref {grad3d}.

a.\(f_x(x,y,z)=10x−2y+3z\),\(f_y(x,y,z)=−2x+2y−4z\), y\( f_z(x,y,z)=3x−4y+2z\), entonces

\ [\ begin {align*}\ vecs f (x, y, z) &=f_x (x, y, z)\,\ hat {\ mathbf i} +f_y (x, y, z)\,\ hat {\ mathbf j} +f_z (x, y, z)\,\ hat {\ mathbf k}\\
& =( 10x−2y+3z)\,\ hat {\ mathbf i} + (−2x+2y−4z)\,\ hat {\ mathbf j} + (3x-4y+2z)\,\ hat {\ mathbf k}. \ end {alinear*}\]

b.\(f_x(x,y,z) =2e^{−2z}\cos 2x \cos 2y\),\( f_y(x,y,z)=−2e^{−2z} \sin 2x \sin 2y\), y\(f_z(x,y,z)=−2e^{−2z}\sin 2x \cos 2y\), entonces

\[\begin{align*} \vecs ∇f(x,y,z) &=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k} \\ &=(2e^{−2z}\cos 2x \cos 2y)\,\hat{\mathbf i}+(−2e^{−2z} \sin 2x \sin 2y)\,\hat{\mathbf j}+(−2e^{−2z}\sin 2x \cos 2y)\,\hat{\mathbf k} \\ &=2e^{−2z}(\cos 2x \cos 2y \,\hat{\mathbf i}−\sin 2x \sin 2y\,\hat{\mathbf j}−\sin 2x \cos 2y\,\hat{\mathbf k}). \end{align*}\]

Ejercicio\(\PageIndex{5}\):

Encuentra el gradiente\(\vecs ∇f(x,y,z)\) de\(f(x,y,z)=\dfrac{x^2−3y^2+z^2}{2x+y−4z.}\)

Contestar

\[\vecs ∇f(x,y,z)=\dfrac{2x^2+2xy+6y^2−8xz−2z^2}{(2x+y−4z)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2−24yz+z^2}{(2x+y−4z)^2}\,\hat{\mathbf j}+\dfrac{4x^2−12y^2−4z^2+4xz+2yz}{(2x+y−4z)^2}\,\hat{\mathbf k}\nonumber \]

La derivada direccional también puede generalizarse a funciones de tres variables. Para determinar una dirección en tres dimensiones, se necesita un vector con tres componentes. Este vector es un vector unitario, y los componentes del vector unitario se denominan cosenos direccionales. Dado un vector unitario tridimensional\(\vecs u\) en forma estándar (es decir, el punto inicial está en el origen), este vector forma tres ángulos diferentes con los ejes positivos\(x\)\(y\) -, - y\(z\) -ejes. Llamemos a estos ángulos\(α,β,\) y\(γ\). Entonces los cosenos direccionales están dados por\(\cos α,\cos β,\) y\(\cos γ\). Estos son los componentes del vector unitario\(\vecs u\); dado que\(\vecs u\) es un vector unitario, es cierto que\(\cos^2 α+\cos^2 β+\cos^2 γ=1.\)

Definición: Derivada direccional de una función de tres variables

Supongamos que\(w=f(x,y,z)\) es una función de tres variables con un dominio de\(D\). Dejar\((x_0,y_0,z_0)∈D\) y dejar\(\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}\) ser un vector de unidad. Entonces, la derivada direccional de\(f\) en la dirección de\(u\) viene dada por

\[D_{\vecs u}f(x_0,y_0,z_0)=\lim_{t→0}\dfrac{f(x_0+t \cos α,y_0+t\cos β,z_0+t\cos γ)−f(x_0,y_0,z_0)}{t} \nonumber \]

siempre que exista el límite.

Podemos calcular la derivada direccional de una función de tres variables usando el gradiente, conduciendo a una fórmula que es análoga a la ecuación\ ref {dd2v}.

Derivada direccional de una función de tres variables

Dejar\(f(x,y,z)\) ser una función diferenciable de tres variables y dejar\(\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}\) ser un vector unitario. Entonces, la derivada direccional de\(f\) en la dirección de\(\vecs u\) viene dada por

\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_z(x,y,z)\cos γ. \label{DDv3} \]

Los tres ángulos\(α,β,\) y\(γ\) determinan el vector unitario\(\vecs u\). En la práctica, podemos usar un vector arbitrario (no unitario), luego dividirlo por su magnitud para obtener un vector unitario en la dirección deseada.

Ejemplo\(\PageIndex{7}\): Finding a Directional Derivative in Three Dimensions

Calcular\(D_{\vecs v}f(1,−2,3)\) en la dirección de\(\vecs v=−\,\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}\) para la función

\[ f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz. \nonumber \]

Solución:

Primero, encontramos la magnitud de\(v\):

\[‖\vecs v‖=\sqrt{(−1)^2+(2)^2+(2)^2}=\sqrt{9}=3. \nonumber \]

Por lo tanto,\(\dfrac{\vecs v}{‖\vecs v‖}=\dfrac{−\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}}{3}=−\dfrac{1}{3}\,\hat{\mathbf i}+\dfrac{2}{3}\,\hat{\mathbf j}+\dfrac{2}{3}\,\hat{\mathbf k}\) es un vector unitario en la dirección de\(\vecs v\), así\(\cos α=−\dfrac{1}{3},\cos β=\dfrac{2}{3},\) y\(\cos γ=\dfrac{2}{3}\). A continuación, calculamos las derivadas parciales de\(f\):

\ [\ begin {alinear*} f_x (x, y, z) &=10x−2y+3z\\
f_y (x, y, z) &=−2x+2y−4z\\
f_z (x, y, z) &=−4y+2z+3x,\ end {align*}\ nonumber\]

luego sustituirlos en Ecuación\ ref {ddV3}:

\ [\ begin {align*} D_ {\ vecs v} f (x, y, z) &=f_x (x, y, z)\ cos α+f_y (x, y, z)\ cos β+f_z (x, y, z)\ cos γ\\
& =( 10x−2y+3z) (−\ dfrac {1} {3}) + (−2x+2y−4z) (\ dfrac {2} {3}) + (−4y+2z+3x) (\ dfrac {2} {3})\\
&=−\ dfrac {10x} {3} +\ dfrac {2y} {3} −\ dfrac {3z} {3} −\ dfrac {4x} 3} +\ dfrac {4y} {3} −\ dfrac {8z} {3} −\ dfrac { 8y} {3} +\ dfrac {4z} {3} +\ dfrac {6x} {3}\\
&=−\ dfrac {8x} {3} −\ dfrac {2y} {3} −\ dfrac {7z} {3}. \ end {alinear*}\]

Por último, para encontrar\(D_{\vecs v}f(1,−2,3),\) sustituimos\(x=1,\, y=−2\), y\(z=3:\)

\ [\ begin {align*} D_ {\ vecs v} f (1, −2,3) &=−\ dfrac {8 (1)} {3} −\ dfrac {2 (−2)} {3}} {3} −\ dfrac {7 (3)} {3}\
&=−\ dfrac {8} {3} +\ dfrac {4} {3} −\ dfrac {21} {3}\\
&=−\ dfrac {25} {3}. \ end {alinear*}\]

Ejercicio\(\PageIndex{6}\):

Calcular\(D_{\vecs v}f(x,y,z)\) y\(D_{\vecs v}f(0,−2,5)\) en la dirección de\(\vecs v=−3\,\hat{\mathbf i}+12\,\hat{\mathbf j}−4\,\hat{\mathbf k}\) para la función

\[f(x,y,z)=3x^2+xy−2y^2+4yz−z^2+2xz.\nonumber \]

Pista

Primero, divida\(\vecs v\) por su magnitud, calcule las derivadas parciales de\(f\), luego use la Ecuación\ ref {ddV3}.

Contestar

\(D_{\vecs v}f(x,y,z)=−\dfrac{3}{13}(6x+y+2z)+\dfrac{12}{13}(x−4y+4z)−\dfrac{4}{13}(2x+4y−2z)\)

\(D_{\vecs v}f(0,−2,5)=\dfrac{384}{13}\)

Resumen

• Una derivada direccional representa una tasa de cambio de una función en cualquier dirección dada.
• El gradiente se puede utilizar en una fórmula para calcular la derivada direccional.
• El gradiente indica la dirección de mayor cambio de una función de más de una variable.

Ecuaciones Clave

• derivado direccional (dos dimensiones)\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \] o\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ\nonumber \]
• gradiente (dos dimensiones)\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\nonumber \]
• gradiente (tres dimensiones)\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}\nonumber \]
• derivado direccional (tres dimensiones)\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_x(x,y,z)\cos γ\nonumber \]

Glosario

Derivada direccional

la derivada de una función en la dirección de un vector unitario dado

gradiente

el gradiente de la función\(f(x,y)\) se define como\(\vecs ∇f(x,y)=(∂f/∂x)\,\hat{\mathbf i}+(∂f/∂y)\,\hat{\mathbf j},\) que puede generalizarse a una función de cualquier número de variables independientes