14.7E: Ejercicios para la Sección 14.7

Última actualización
Guardar como PDF

Page ID: 116222

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Encontrar puntos críticos

En los ejercicios 1 - 5, encuentra todos los puntos críticos.

1)$ f(x,y)=1+x^2+y^2$

Responder: $ (0,0)$

2)$ f(x, y) = 1 - (x -2)^2 + (y+3)^2$

3)$ f(x,y)=(3x−2)^2+(y−4)^2$

Responder: $ \left(\frac{2}{3},4\right)$

4)$ f(x,y)=x^4+y^4−16xy$

Responder: $ (0,0), \quad (-2,-2), \quad (2,2)$

5)$ f(x,y)=15x^3−3xy+15y^3$

Responder: $ (0,0), \quad \left(\frac{1}{15},\frac{1}{15}\right)$

Encontrar Extrema y la Segunda Prueba de Partiales

En los ejercicios 6 - 9, encuentra los puntos críticos de la función y prueba para puntos extremos o sillín usando técnicas algebraicas (completando el cuadrado) o examinando la forma de la ecuación. En la medida de lo posible, verifica tus resultados usando la Segunda Prueba de Parciales.

6)$ f(x,y)=-\sqrt{x^2+y^2}$

Responder: Crit. pts.:$ (0, 0) $
Extrema:$ f$ tiene un máximo relativo de$0$ at$ (0, 0)$.
Para justificar esto, considere el hecho de que la función raíz cuadrada no puede dar un valor negativo, por lo que esta función no puede devolver un valor positivo. Ya que su valor está$0$ en el punto crítico$ (0, 0)$, sabemos que debe ser el valor máximo absoluto de la función.

7)$ f(x,y)=−x^2−5y^2+8x−10y−13$

Responder: Crit. pts.:$ (4, -1) $
Extrema:$ f$ tiene un máximo relativo de$8$ at$ (4,−1)$.
Para justificar esto, completamos el cuadrado en esta función, teniendo cuidado de factorizar el coeficiente de los términos cuadrados antes de completar el cuadrado.
\[\begin{align*} f(x, y) &= −x^2−5y^2+8x−10y−13 \\ &= −(x^2-8x\quad\quad)−5(y^2+2y\quad\quad)−13 \\ &= −(x^2-8x+16)−5(y^2+2y+1)−13+16+5 \\ &= -(x-4)^2 -5(y+1)^2+8\end{align*}\]
Obsérvese que esta función polinómica cuadrática toma la forma$ z = -(x^2 + y^2)$, por lo que podemos ver que tendrá un máximo relativo (y, de hecho, absoluto) en su vértice (el punto crítico$ (4, -1) $). También podemos argumentar que como estamos restando términos cuadrados de 8, no podemos obtener un valor de función mayor a 8, y como sí obtenemos un valor de 8 en el punto crítico$ (4, -1) $, sabemos que será el valor máximo absoluto de esta función.

8)$ f(x,y)=x^2+y^2+2x−6y+6$

9)$ f(x,y)=\sqrt{x^2+y^2}+1$

Responder: Crit. Pts.:$ (0, 0) $
Extrema:$ f$ tiene un mínimo relativo de$1$ at$ (0,0)$.
Para justificar esto, considere el hecho de que la función raíz cuadrada no puede dar un valor negativo, por lo que esta función no puede devolver un valor menor que$1$. Ya que su valor está$1$ en el punto crítico$ (0, 0)$, sabemos que$1$ debe ser el valor mínimo absoluto de la función.

En los ejercicios 10 - 34, identificar cualquier punto crítico y utilizar la Segunda Prueba de Patiales para determinar el comportamiento de la función en cada punto crítico, ya sea que exista un punto máximo, mínimo, de silla de montar, o ninguno de estos. Si falla la Segunda Prueba de Parciales, determina el comportamiento de la función en ese punto usando otro método y justifica tu respuesta con claridad.

10)$ f(x,y)=−x^3+4xy−2y^2+1$

11)$ f(x,y)=x^2y^2$

Responder: Crit. pts.: Todos los puntos en las líneas$ x = 0 $ y$ y = 0$ son puntos críticos de esta función.
Exrema: La Segunda Prueba Parcial falla.
Dado que$ x^2y^2>0$ para todos$ x$ y$ y$ diferente de cero, y$ x^2y^2=0$ cuando cualquiera$ x$ o$ y$ es igual a cero (o ambos), entonces el mínimo absoluto de$0$ ocurre en todos los puntos en los ejes$x$ - o$y$ -ejes, es decir, para todos los puntos en el líneas$ x = 0 $ y$ y = 0$.

12)$ f(x,y)=x^2−6x+y^2+4y−8$

13)$ f(x,y)=2xy+3x+4y$

Responder: Crit. pts.:$ \left(−2,−\frac{3}{2}\right) $
Exrema:$f$ tiene una punta de sillín en$ \left(−2,−\frac{3}{2},−6\right) $.

14)$ f(x,y)=8xy(x+y)+7$

15)$ f(x,y)=x^2+4xy+y^2$

Responder: Crit. pts.:$ (0,0) $
Exrema:$f$ tiene una punta de sillín en$ (0,0,0)$.

16)$ f(x,y)=x^3+y^3−300x−75y−3$

17)$ f(x,y)=9−x^4y^4$

Contestar: Crit. pts.: Todos los puntos en las líneas$ x = 0 $ y$ y = 0$ son puntos críticos de esta función.
Extrema: La Segunda Prueba Parcial falla.
Dado que el término$ -x^4y^4<0$ para todos$ x$ y$ y$ diferente de cero, y$ -x^4y^4=0$ cuando cualquiera$ x$ o$ y$ es igual a cero (o ambos), entonces esta función no puede alcanzar un valor mayor que en$9$ cualquier lugar, sino que está$9$ en los puntos críticos. Así$f$ tiene un máximo$9$ absoluto de en todos los puntos en los$x$ -o$y$ -ejes, es decir, para todos los puntos en las líneas$ x = 0 $ y$ y = 0$.

18)$ f(x,y)=x^2+10xy+y^2$

Contestar: Crit. pts.:$ (0,0) $
Extrema:$f$ tiene una punta de sillín en$ (0,0,0)$.

19)$f(x,y) = x^4 + y^2 + 2xy + 3$

Contestar: Crit. pts.:$ (0,0), \quad \left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right), \quad \left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right) $
Extrema:$f$ tiene una punta de sillín en$ (0, 0, 3) $,
$f$ tiene un mínimo local de$ 2.75$ en el punto$ \left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right) $.
$f$tiene un mínimo local de$ 2.75$ en el punto$ \left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right) $.

20)$ f(x,y)=7x^2y+9xy^2$

21)$ f(x,y)=3x^2−2xy+y^2−8y$

Contestar: Crit. pts.:$ (2,6) $
Extrema:$f$ tiene un mínimo relativo de$ -24$ ubicado en$ (2,6)$.

22)$ f(x,y)=3x^2+2xy+y^2$

23)$ f(x,y)=y^2+xy+3y+2x+3$

Contestar: Crit. pts.:$ (1,−2) $
Extrema:$f$ tiene una punta de sillín en$ (1,−2,1)$.

24)$ f(x,y)=x^2+xy+y^2−3x$

25)$ f(x,y)=x^2+2y^2−x^2y$

Contestar: Crit. pts.:$ (0,0), \quad (-2,1), \quad (2,1)$
Extrema:$f$ tiene un mínimo relativo de$0$ at$ (0,0) $ y puntos de sillín en$ (2,1,2)$ y$ (−2,1,2)$.

26)$ f(x,y)=x^2+y−e^y$

27)$ f(x,y)=e^{−(x^2+y^2+2x)}$

Contestar: Crit. pts.:$ (-1,0) $
Extrema:$f$ tiene un máximo relativo de$ e $ ubicado en$ (-1,0)$.
Ver este problema ilustrado en CalcPlot3D.

28)$ f(x,y)=x^2+xy+y^2−x−y+1$

29)$f(x,y) = x^2y(9 - x + y)$

Contestar: Crit. pts.:$ \left(\frac{9}{2},-\frac{9}{4}\right), \quad (9,0)$, y todos los puntos de la línea$x = 0$
Extrema:$f$ tiene un punto de sillín en$ (9,0,0)$ y un mínimo relativo de$-102.515625$ at$ \left(\frac{9}{2},-\frac{9}{4}\right)$.
En los puntos críticos de la línea$x = 0$, no$f$ tiene ni extremos relativos ni puntos de sillín, pero sí representan una especie de depresión en la superficie.

30)$ f(x,y)=−x^2−5y^2+10x−30y−62$

31)$ f(x,y)=120x+120y−xy−x^2−y^2$

Contestar: Crit. pts.:$ (40,40) $
Extrema:$f$ tiene un máximo relativo de$ 4800 $ ubicado en$ (40,40)$.

32)$ f(x,y)=2x^2+2xy+y^2+2x−3$

33)$ f(x,y)=x^2+x−3xy+y^3−5$

Contestar: Crit. pts.:$ \left(\frac{1}{4},\frac{1}{2}\right)$ y$(1, 1) $
Extrema:$f$ tiene un punto de sillín en$ \left(\frac{1}{4},\frac{1}{2}, -\frac{79}{16}\right)$ y un mínimo relativo de$ -5 $ at$ (1,1)$.

34)$ f(x,y)=2xye^{−x^2−y^2}$

En los ejercicios 35 - 37, determinar los valores extremos y los puntos de sillín. Utilice un CAS para graficar la función.

35) [T]$ f(x,y)=ye^x−e^y$

Contestar

Un punto de sillín se encuentra en$ (0,0,-1).$

36) [T]$ f(x,y)=x\sin(y)$

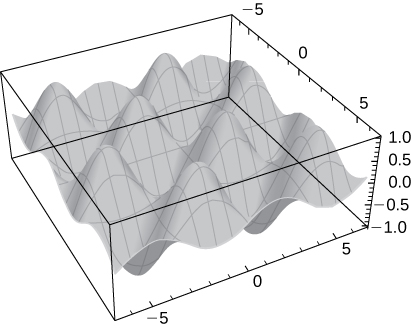
37) [T]$ f(x,y)=\sin(x)\sin(y),\quad x∈(0,2π),\quad y∈(0,2π)$

Contestar

Hay un punto de silla de montar en los máximos$ (π,π),$ locales en$ \left(\frac{π}{2},\frac{π}{2}\right)$ y$ \left(\frac{3π}{2},\frac{3π}{2}\right)$, y mínimos locales en$ \left(\frac{π}{2},\frac{3π}{2}\right)$ y$ \left(\frac{3π}{2},\frac{π}{2}\right)$.

$Gráfica superficial de la función f (x, y) = sin (x) sin (y)$

En los ejercicios 38 - 41, encuentra los extremos absolutos de la función dada en el conjunto cerrado y acotado indicado$R$.

38)$f(x,y)=xy−x−3y$ donde$R$ está la región triangular con vértices$(0,0), \, (0,4),$ y$(5,0)$.

39) Encuentra los valores máximos y mínimos absolutos de$f(x,y)=x^2+y^2−2y+1$ en la región$R=\big\{(x,y) \, | \, x^2+y^2≤4\big\}.$

Contestar: $(0,1,0)$es el mínimo absoluto y$(0,−2,9)$ es el máximo absoluto.

40)$f(x,y)=x^3−3xy−y^3$ en$R=\big\{(x,y) \, | \, −2≤x≤2,\;−2≤y≤2\big\}$

41)$f(x,y)=\dfrac{−2y}{x^2+y^2+1}$ en$R=\big\{(x,y) \, | \, x^2+y^2≤4\big\}$

Contestar: Hay un mínimo absoluto en$(0,1,−1)$ y un máximo absoluto en$(0,−1,1)$.

42) Encuentra tres números positivos cuya suma sea$27$, de tal manera que la suma de sus cuadrados sea lo más pequeña posible.

43) Encuentra los puntos en la superficie$x^2−yz=5$ que están más cerca del origen.

Contestar: $\left(\sqrt{5},0,0\right), \; \left(−\sqrt{5},0,0\right)$

44) Encuentra el volumen máximo de una caja rectangular con tres caras en los planos de coordenadas y un vértice en el primer octante de la línea$x+y+z=1$.

45) La suma de la longitud y la circunferencia (perímetro de una sección transversal) de un paquete transportado por un servicio de entrega no puede exceder$108$ en. Encuentra las dimensiones del paquete rectangular de mayor volumen que se puede enviar.

Contestar: $18$$36$por$18$ en.

46) Una caja de cartón sin tapa se debe hacer con un volumen de$4$ ft ³. Encuentra las dimensiones de la caja que requiere la menor cantidad de cartón.

47) Encuentra el punto en la superficie$f(x,y)=x^2+y^2+10$ más cercano al plano$x+2y−z=0.$ Identificar el punto en el plano.

Contestar: $\left(\frac{47}{24},\frac{47}{12},\frac{235}{24}\right)$

48) Encuentra el punto en el plano$2x−y+2z=16$ que está más cerca del origen.

49) Una empresa fabrica dos tipos de calzado deportivo: zapatillas para correr y zapatillas cruzadas. El ingreso total por$x$ unidades de zapatillas para correr y$y$ unidades de cross-trainers viene dado por$R(x,y)=−5x^2−8y^2−2xy+42x+102y,$ dónde$x$ y$y$ están en miles de unidades. Encuentra los valores de$x$ y$y$ para maximizar los ingresos totales.

Contestar: $x=3$y$y=6$

50) Una naviera maneja cajas rectangulares siempre que la suma de la longitud, anchura y altura de la caja no exceda$96$ en. Encuentra las dimensiones de la caja que cumple con esta condición y tiene el mayor volumen.

51) Encuentra el volumen máximo de una lata de soda cilíndrica de tal manera que la suma de su altura y circunferencia sea$120$ cm.

Contestar: $V=\dfrac{64,000}{π}≈20,372\text{ cm}^3$

Colaboradores

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) creó los problemas 19 y 29, y agregó cifras dinámicas para los problemas 27 y 35.