1.7: Coordenadas curvilíneas
- Page ID
- 111258
Las coordenadas cartesianas de un punto\((x, y, z)\) se determinan siguiendo trayectorias rectas que parten del origen: primero a lo largo del\(x\) eje -y luego paralelas al\(y\) eje -y luego paralelas al\(z\) eje -como en la Figura 1.7.1. En los sistemas de coordenadas curvilíneas, estos caminos pueden ser curvos. Los dos tipos de coordenadas curvilíneas que consideraremos son coordenadas cilíndricas y esféricas. En lugar de hacer referencia a un punto en términos de lados de un paralelepípedo rectangular, como ocurre con las coordenadas cartesianas, pensaremos que el punto está acostado sobre un cilindro o esfera. Las coordenadas cilíndricas se utilizan a menudo cuando hay simetría alrededor del\(z\) eje; las coordenadas esféricas son útiles cuando hay simetría sobre el origen.
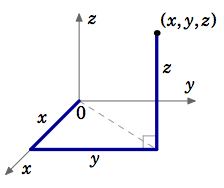
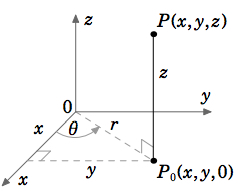
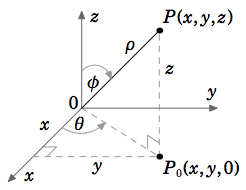
Dejar\(P = (x, y, z)\) ser un punto en las coordenadas cartesianas en\(\mathbb{R}^ 3\), y dejar\(P_0 = (x, y,0)\) ser la proyección de\(P\) sobre el\(x y\) plano. Tratando\((x, y)\) como un punto en\(\mathbb{R}^2\), dejar\((r,θ)\) ser sus coordenadas polares (ver Figura 1.7.2). Dejar\(ρ\) ser la longitud del segmento de línea desde el origen hasta\(P\), y dejar que\(φ\) sea el ángulo entre ese segmento de línea y el\(z\) eje positivo (ver Figura 1.7.3). \(φ\)se llama el ángulo cenital. Luego las coordenadas cilíndricas\((r,θ, z)\) y las coordenadas esféricas\((ρ,θ,φ)\) de\(P(x, y, z)\) se definen de la siguiente manera:
Coordenadas cilíndricas (r, θ, z)
\[\nonumber \begin{split} x &= r \cos θ \qquad r &= \sqrt{ x^ 2 + y^ 2} \\[4pt] \nonumber y &= r \sin θ \qquad θ &= \tan^{−1} \left ( \dfrac{ y}{ x}\right ) \\[4pt] \nonumber z &= z \qquad \qquad z &= z \\[4pt] \end{split}\]
donde\(0 ≤ θ ≤ π \text{ if }y ≥ 0 \text{ and }π < θ < 2π \text{ if }y < 0\)
Coordenadas esféricas (ρ, θ, φ)
\[\nonumber \begin{split} x &= ρ \sin φ \cos θ \qquad &ρ = \sqrt{ x^ 2 + y^ 2 + z^ 2} \\[4pt] \nonumber y &= ρ \sin φ \sin θ \qquad \qquad &θ = \tan^{−1}\left ( \dfrac{ y}{ x} \right ) \\[4pt] \nonumber z &= ρ \cos φ \qquad \qquad &φ = \cos^{−1} \left ( \dfrac{ z}{ x^ 2+y^ 2+z^ 2} \right ) \\[4pt] \end{split}\]
donde\(0 ≤ θ ≤ π \text{ if }y ≥ 0 \text{ and }π < θ < 2π \text{ if }y < 0\)
Ambos\(θ\) y\(φ\) se miden en radianes. Tenga en cuenta que\(r ≥ 0, \, 0 ≤ θ < 2π,\, ρ ≥ 0 \text{ and }0 ≤ φ ≤ π\). Además, no\(θ\) está definido cuando\((x, y) = (0,0)\), y\(φ\) es indefinido cuando\((x, y, z) = (0,0,0)\).
Ejemplo 1.31
Convertir el punto\((−2,−2,1)\) de coordenadas cartesianas a (a) coordenadas cilíndricas y (b) esféricas.
Solución
(a)\(r = \sqrt{ (−2)^2 +(−2)^2} = 2\sqrt{ 2},\, θ = \tan^{−1} \left ( \dfrac{−2}{ −2} \right ) = \tan^{−1} (1) = \dfrac{5π}{ 4} ,\text{ since }y = −2 < 0\)
\(∴ (r,θ, z) =\left ( 2 \sqrt{ 2}, \dfrac{5π}{ 4} ,1 \right ) \)
b)\(ρ = \sqrt{ (−2)^2 +(−2)^2 +1^ 2} = \sqrt{ 9} = 3,\, φ = \cos^{−1} \left ( \dfrac{1}{ 3} \right ) ≈ 1.23 \text{ radians}\).
\(∴ (ρ,θ,φ) = \left ( 3, \dfrac{5π}{ 4} ,1.23 \right ) \)
Para coordenadas cilíndricas\((r,θ, z)\), y constantes\(r_0 , θ_0 \text{ and }z_0\), vemos en la Figura 1.7.4 que la superficie\(r = r_0\) es un cilindro de radio\(r_0\) centrado a lo largo del\(z\) eje -eje, la superficie\(θ = θ_0\) es un medio plano que emana\(z\) del eje -y la superficie\(z = z_0\) es un plano paralelo al\(x y\) plano.
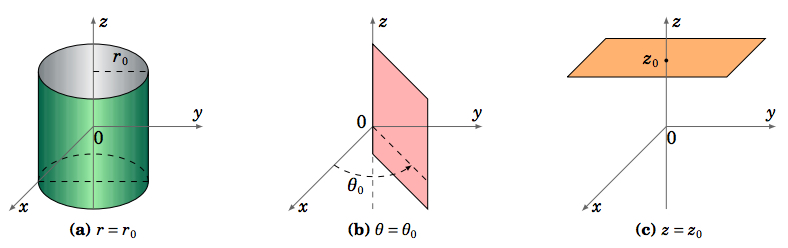
Para coordenadas esféricas\((ρ,θ,φ)\), y constantes\(ρ_0 , θ_0 \text{ and }φ_0\), vemos en la Figura 1.7.5 que la superficie\(ρ = ρ_0\) es una esfera de radio\(ρ_0\) centrada en el origen, la superficie\(θ = θ_0\) es un semiplano que emana del\(z\) eje -y la superficie\(φ = φ_0\) es un cono circular cuyo vértice está en el origen.
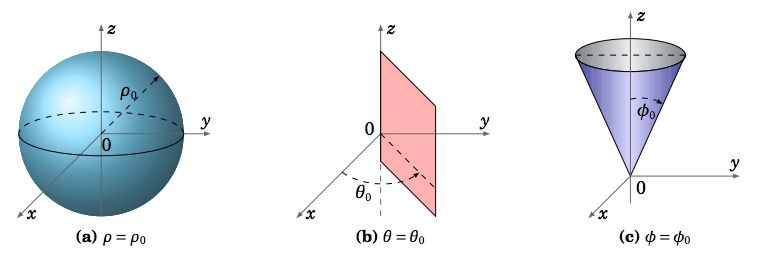
Las figuras 1.7.4 (a) y 1.7.5 (a) muestran cómo estos sistemas de coordenadas obtuvieron sus nombres.
En ocasiones la ecuación de una superficie en coordenadas cartesianas se puede transformar en una ecuación más simple en algún otro sistema de coordenadas, como en el siguiente ejemplo.
Ejemplo 1.32
Escribe la ecuación del cilindro\(x^ 2 + y^ 2 = 4\) en coordenadas cilíndricas.
Desde\(r = \sqrt{ x^ 2 + y^ 2}\) entonces la ecuación en coordenadas cilíndricas es\(r = 2\).
El uso de coordenadas esféricas para escribir la ecuación de una esfera no necesariamente simplifica la ecuación, si la esfera no está centrada en el origen.
Ejemplo 1.33
Escribe la ecuación\((x−2)^2 +(y−1)^2 + z^ 2 = 9\) en coordenadas esféricas.
Solución
Multiplicar la ecuación da
\[\begin{align}\nonumber x^ 2 + y^ 2 + z^ 2 −4x−2y+5 &= 9 , \text{ so we get} \\[4pt] \nonumber ρ^ 2 −4ρ \sin φ \cos θ −2ρ \sin φ \sin θ −4 &= 0 , \text{ or} \\[4pt] \nonumber ρ^ 2 −2\sin φ(2\cos θ −\sin θ )ρ −4 &= 0 \\[4pt] \end{align}\]
después de combinar términos. Tenga en cuenta que esto en realidad hace que sea más difícil averiguar cuál es la superficie, a diferencia de la ecuación cartesiana donde podría identificar inmediatamente la superficie como una esfera de radio 3 centrada en\((2,1,0)\).
Ejemplo 1.34
Describir la superficie dada por\(θ = z\) en coordenadas cilíndricas.
Solución
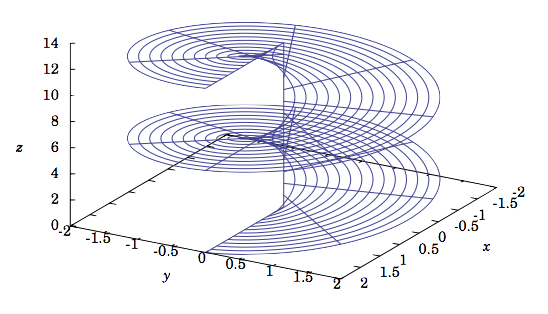
Esta superficie se llama helicoide. A medida que aumenta la\(z\) coordenada (vertical), también lo hace el ángulo\(θ\), mientras que el radio no\(r\) tiene restricciones. Entonces esto barre un (¡descartado!) superficie con forma de escalera de caracol, donde la espiral tiene un radio infinito. La Figura 1.7.6 muestra una sección de esta superficie restringida a\(0 ≤ z ≤ 4π \text{ and }0 ≤ r ≤ 2\).
