1.8: Funciones con valores vectoriales
( \newcommand{\kernel}{\mathrm{null}\,}\)
Ahora que estamos familiarizados con los vectores y sus operaciones, podemos comenzar a discutir funciones cuyos valores son vectores.
Definición 1.10
Una función con valor vectorial de una variable real es una regla que asocia un vectorf(t) con un número realt, dondet está en algún subconjuntoD deR1 (llamado dominio def). Escribimos f:D→R3 para denotar que f es un mapeo deD enR3.
Por ejemplo,f(t)=ti+t2j+t3k es una función vectorizada enR3, definida para todos los números realest. Escribiríamos f:R→R3. Alt=1 valor de la función se encuentra el vector i + j + k, que en coordenadas cartesianas tiene el punto terminal(1,1,1).
Una función de valor vectorial de una variable real se puede escribir en forma de componente como
f(t)=f1(t)i+f2(t)j+f3(t)k
o en la forma
f(t)=(f1(t),f2(t),f3(t))
para algunas funciones de valor realf1(t),f2(t),f3(t), llamadas funciones componentes de f. La primera forma se usa a menudo cuando se enfatiza quef(t) es un vector, y la segunda forma es útil cuando se consideran solo los puntos terminales de los vectores. Al identificar vectores con sus puntos terminales, se puede escribir una curva en el espacio como una función de valor vectorial.
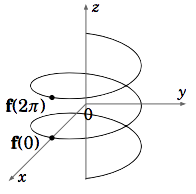
Ejemplo 1.35
Definir f:R→R3 porf(t)=(cost,sint,t). Esta es la ecuación de una hélice (ver Figura 1.8.1). A medida quet aumenta el valor de, los puntos terminales def(t) trazan una curva en espiral hacia arriba. Para cada unot, lasx− and y− coordenadas def(t) are x=cost and y=sint, entonces
x2+y2=cos2t+sin2t=1
Así, la curva se encuentra en la superficie del cilindro circular derechox2+y2=1.
Puede ayudar pensar en las funciones vectoriales de una variable real enR3 como una generalización de las funciones paramétricas en lasR2 que aprendió en el cálculo de una sola variable. Gran parte de la teoría de las funciones de valor real de una sola variable real se puede aplicar a las funciones vectoriales de una variable real. Dado que cada una de las tres funciones componentes son de valor real, a veces será el caso de que los resultados del cálculo de una sola variable simplemente se puedan aplicar a cada una de las funciones componentes para producir un resultado similar para la función de valor vectorial. No obstante, hay momentos en que tales generalizaciones no se mantienen (ver Ejercicio 13). El concepto de límite, sin embargo, se puede extender de forma natural a las funciones de valor vectorial, como en la siguiente definición.
Definición 1.11
Dejarf(t) ser una función con valor vectorial, dejara ser un número real y dejar que c sea un vector. Entonces decimos que el límite def(t) como set acercaa es igual a c, escrito comolimt→af(t)=c, silimt→a‖f(t)−c‖=0. Sif(t)=(f1(t),f2(t),f3(t)), entonces
limt→af(t)=(limt→af1(t),limt→af2(t),limt→af3(t))
siempre que existan los tres límites del lado derecho.
La definición anterior muestra que la continuidad y la derivada de funciones vectoriales también pueden definirse en términos de sus funciones componentes.
Definición 1.12
Dejarf(t)=(f1(t),f2(t),f3(t)) ser una función vectorizada, y dejara ser un número real en su dominio. Entoncesf(t) es continuo ena silimt→af(t)=f(a). Equivalentemente,f(t) es continuo ena si y solo sif1(t),f2(t), and f3(t) son continuos ena.
La derivada def(t) ata, denotada porf′(a) odfdt(a), es el límite
f′(a)=limh→0f(a+h)−f(a)h
si ese límite existe. Equivalentementef′(a)=(f1′(a),f2′(a),f3′(a)),, si existen los derivados componentes. Decimos quef(t) es diferenciable ena sif′(a) existe.
Recordemos que la derivada de una función de valor real de una sola variable es un número real, que representa la pendiente de la línea tangente a la gráfica de la función en un punto. Del mismo modo, la derivada de una función de valor vectorial es un vector tangente a la curva en el espacio que representa la función, y se encuentra en la línea tangente a la curva (ver Figura 1.8.2).
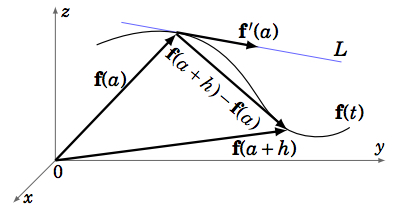
Ejemplo 1.36
Vamosf(t)=(cost,sint,t). Entoncesf′(t)=(−sint,cost,1) for all t. La línea tangenteL a la curva enf(2π)=(1,0,2π) is L=f(2π)+sf′(2π)=(1,0,2π)+s(0,1,1), o en forma paramétrica:x=1,y=s,z=2π+s for −∞<s<∞.
Una función escalar es una función de valor real. Obsérvese que siu(t) es una función escalar yf(t) es una función de valor vectorial, entonces su producto, definido por (uf)(t)=u(t)f(t)para todost, es una función valorada por vector (ya que el producto de un escalar con un vector es un vector).
Las propiedades básicas de las derivadas de funciones vectoriales se resumen en el siguiente teorema.
Teorema 1.20
Dejarf(t) and g(t) ser funciones vectorizadas diferenciables, dejaru(t) ser una función escalar diferenciable, dejark ser un escalar, y dejar que c sea un vector constante. Entonces
- ddt(c)=0
- ddt(kf)=kdfdt
- ddt(f+g)=dfdt+dgdt
- ddt(f−g)=dfdt−dgdt
- ddt(uf)=dudtf+udfdt
- ddt(f·g)=dfdt·g+f·dgdt
- ddt(f×g)=dfdt×g+f×dgdt
Prueba
Las pruebas de las partes (a) - (e) siguen fácilmente diferenciando las funciones de los componentes y usando las reglas para derivadas del cálculo de una sola variable. Demostraremos la parte (f), y dejaremos el comprobante de la parte (g) como ejercicio para el lector.
(f) Escribirf(t)=(f1(t),f2(t),f3(t)) and g(t)=(g1(t),g2(t),g3(t)), donde todas las funciones componentesf1(t),f2(t),f3(t),g1(t),g2(t),g3(t) son funciones diferenciables de valor real. Entonces
\[\nonumber \begin{align}\dfrac{d}{dt} (\textbf{f}(t)· \textbf{g}(t))&=\dfrac{d}{ dt} (f_1(t) g_1(t)+ f_2(t) g_2(t)+ f_3(t) g_3(t)) \\[4pt] \nonumber &= \dfrac{d}{ dt} (f_1(t) g_1(t))+ \dfrac{d}{ dt} (f_2(t) g_2(t))+ \dfrac{d}{ dt} (f_3(t) g_3(t)) \\[4pt] \nonumber &=\dfrac{d f_1}{ dt} (t) g_1(t)+ f_1(t)\dfrac{ d g_1}{ dt} (t)+ \dfrac{d f_2}{ dt} (t) g_2(t)+ f_2(t) \dfrac{d g_2}{ dt} (t)+ \dfrac{d f_3}{ dt} (t) g_3(t)+ f_3(t) \dfrac{d g_3}{ dt} (t) \\[4pt] \nonumber &=\left ( \dfrac{d f_1}{ dt} (t),\dfrac{d f_2}{ dt} (t), \dfrac{d f_3}{ dt} (t) \right ) · (g_1(t), g_2(t), g_3(t)) \\[4pt] \nonumber &\quad +(f_1(t), f_2(t), f_3(t))· \left ( \dfrac{d g_1}{ dt} (t), \dfrac{d g_2}{ dt} (t), \dfrac{d g_3}{ dt} (t)\right ) \\[4pt] \nonumber &=\dfrac{d\textbf{f}}{ dt} (t)· \textbf{g}(t) + \textbf{f}(t)· \dfrac{d\textbf{g}}{ dt} (t) \text{ for all }t.\tag{QED} \\boldsymbol{4pt] \end{align}}
◻
Ejemplo 1.37
Supongamos quef(t) es diferenciable. Encuentra la derivada de‖f(t)‖.
Dado que‖f(t)‖ es una función de valor real det, entonces por la Regla de Cadena para funciones de valor real, lo sabemosddt‖f(t)‖2=2‖f(t)‖ddt‖f(t)‖.
Pero‖f(t)‖2=f(t)·f(t), entoncesddt‖f(t)‖2=ddt(f(t)·f(t)). Por lo tanto, tenemos
2‖f(t)‖ddt‖f(t)‖=ddt(f(t)·f(t))=f′(t)·f(t)+f(t)·f′(t) by Theorem 1.20(f), so=2f′(t)·f(t), so if ‖f(t)‖≠0 thenddt‖f(t)‖=f′(t)·f(t)‖f(t)‖
Sabemos que‖f(t)‖ es constante si y sólo siddt‖f(t)‖=0 por todost. También,f(t)⊥f′(t) if and only if f′(t)·f(t)=0. Así, el ejemplo anterior muestra este importante hecho:
Si‖f(t)‖≠0, then ‖f(t)‖ is constant if and only if f(t)⊥f′(t) for all t.
Esto significa que si una curva se encuentra completamente sobre una esfera (o círculo) centrada en el origen, entonces el vector tangente siempref′(t) es perpendicular al vector de posiciónf(t).
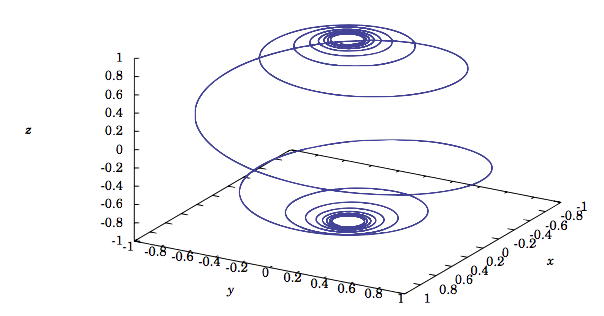
Ejemplo 1.38
La espiral esféricaf(t)=(cost√1+a2t2,sint√1+a2t2,−at√1+a2t2), paraa≠0.
La Figura 1.8.3 muestra la gráfica de la curva cuandoa=0.2. En los ejercicios, se le pedirá al lector que demuestre que esta curva se encuentra en la esferax2+y2+z2=1 y que verifique directamente esof′(t)·f(t)=0 for all t.
Al igual que en el cálculo de una sola variable, las derivadas de orden superior de las funciones con valores vectoriales se obtienen diferenciando repetidamente la (primera) derivada de la función:
\[\nonumber \textbf{f} ′′(t) = \dfrac{d}{ dt} \textbf{f} ′ (t) ,\qquad \textbf{f} ′′′(t) = \dfrac{d}{ dt} \textbf{f} ′′(t) , ... , \dfrac{d^ n \textbf{f}}{ dt^n} = \dfrac{d}{ dt} \left ( \dfrac{d^{n−1}\textbf{f}}{ dt^{n−1}} \right ) \text{ (for n=2,3,4,...)}\]
Podemos usar funciones vectoriales para representar cantidades físicas, como velocidad, aceleración, fuerza, impulso, etc. Por ejemplo, dejar que la variable realt represente el tiempo transcurrido desde algún tiempo inicial (t=0), y supongamos que un objeto de masa constantem está sujeto a alguna fuerza para que se mueva en el espacio, con su posición (x,y,z) en el tiempot una función det. Es decir,x=x(t),y=y(t),z=z(t) para algunas funciones de valor realx(t),y(t),z(t). Llamer(t)=(x(t),y(t),z(t)) al vector de posición del objeto. Podemos definir varias cantidades físicas asociadas al objeto de la siguiente manera:
position:r(t)=(x(t),y(t),z(t))velocity:v(t)=˙r(t)=r′(t)=drdt=(x′(t),y′(t),z′(t))acceleration:a(t)=˙v(t)=v′(t)=dvdt=¨r(t)=r′′(t)=d2rdt2=(x′′(t),y′′(t),z′′(t))momentum:p(t)=mv(t)force:F(t)=˙p(t)=p′(t)=dpdt (Newton’s Second Law of Motion)
La magnitud‖v(t)‖ del vector de velocidad se llama velocidad del objeto. Tenga en cuenta que dado que la masam es una constante, la ecuación de fuerza se vuelve familiarF(t)=ma(t).
Ejemplo 1.39
Dejarr(t)=(5cost,3sint,4sint) ser el vector de posición de un objeto a la vezt≥0. Encuentra sus vectores (a) de velocidad y (b) de aceleración.
Solución
- v(t)=˙r(t)=(−5sint,3cost,4cost)
- a(t)=˙v(t)=(−5cost,−3sint,−4sint)
Tenga en cuenta que‖r(t)‖=√25cos2t+25sin2t=5 para todost, así que por Ejemplo 1.37 sabemos esor(t)·˙r(t)=0 for all t (que podemos verificar desde la parte (a)). De hecho,‖v(t)‖=5 para todost también. Y no sólo ser(t) encuentra sobre la esfera de radio 5 centrada en el origen, sino que quizás no tan obvio es que se encuentra completamente dentro de un círculo de radio 5 centrado en el origen. También, tenga en cuenta quea(t)=−r(t). Resulta (ver Ejercicio 16) que cada vez que un objeto se mueve en un círculo con velocidad constante, el vector de aceleración apuntará en la dirección opuesta al vector de posición (es decir, hacia el centro del círculo).
Recordemos de la Sección 1.5 que sir1,r2 son vectores de posición a puntos distintos, entoncesr1+t(r2−r1) representa una línea a través de esos dos puntos, ya quet varía sobre todos los números reales. Esa suma vectorial se puede escribir como(1−t)r1+tr2. Entonces la funciónl(t)=(1−t)r1+tr2 es una línea a través de los puntos terminales der1 and r2, y cuandot se restringe al intervalo[0,1] es el segmento de línea entre los puntos, conl(0)=r1 and l(1)=r2.
En general, una función de la formaf(t)=(a1t+b1,a2t+b2,a3t+b3) representa una línea enR3. Una función de la formaf(t)=(a1t2+b1t+c1,a2t2+b2t+c2,a3t2+b3t+c3) representa una parábola (posiblemente degenerada) enR3.
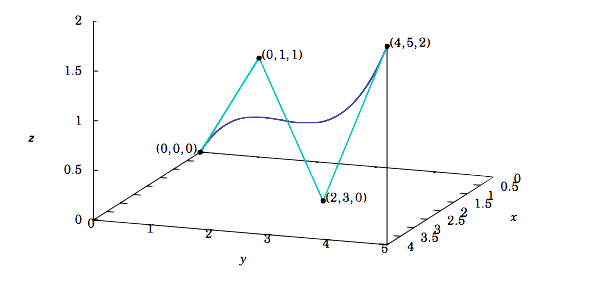
Ejemplo 1.40: Curvas Bézier
Las curvas Bézier se utilizan en Diseño Asistido por Computadora (CAD) para aproximar la forma de un camino poligonal en el espacio (llamado polígono Bézier o polígono de control). Por ejemplo, dados tres puntos (o vectores de posición)b0,b1,b2 in R3, definir
b10(t)=(1−t)b0+tb1b11(t)=(1−t)b1+tb2b20(t)=(1−t)b10(t)+tb11(t)=(1−t)2b0+2t(1−t)b1+t2b2
para todos los realest. Porquet en el intervalo[0,1], vemos queb10(t) es el segmento de línea entreb0 and b1, yb11(t) es el segmento de línea entreb1 and b2. La funciónb20(t) es la curva Bézier para los puntosb0,b1,b2. Observe de la última fórmula que la curva es una parábola que pasa porb0 (cuándot=0) yb2 (cuándot=1).
Como ejemplo, vamosb0=(0,0,0),b1=(1,2,3), and b2=(4,5,2). Entonces la fórmula explícita para la curva Bézier esb20(t)=(2t+2t2,4t+t2,6t−4t2), como se muestra en la Figura 1.8.4, donde están los segmentos de líneab10(t) and b11(t), y la curva esb20(t).
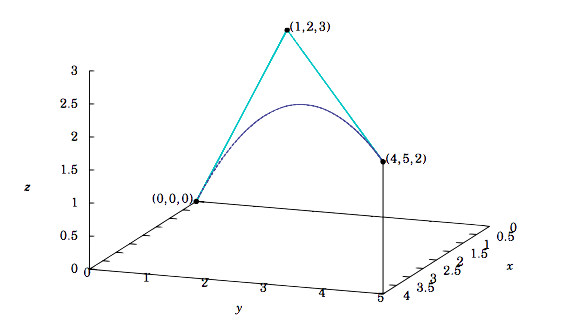
En general, la trayectoria poligonal determinada por puntosn≥3 no colineales en seR3 puede utilizar para definir la curva Bézier recursivamente mediante un proceso llamado interpolación lineal repetida. Esta curva será una función de valor vectorial cuyos componentes son polinomios de gradon−1, y su fórmula viene dada por el algoritmo de Casteljau. En los ejercicios, se le dará al lector el algoritmo para el caso de losn=4 puntos y se le pedirá que escriba la fórmula explícita para la curva Bézier para los cuatro puntos mostrados en la Figura 1.8.5.