2.3: Plano tangente a una superficie
- Page ID
- 111361
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
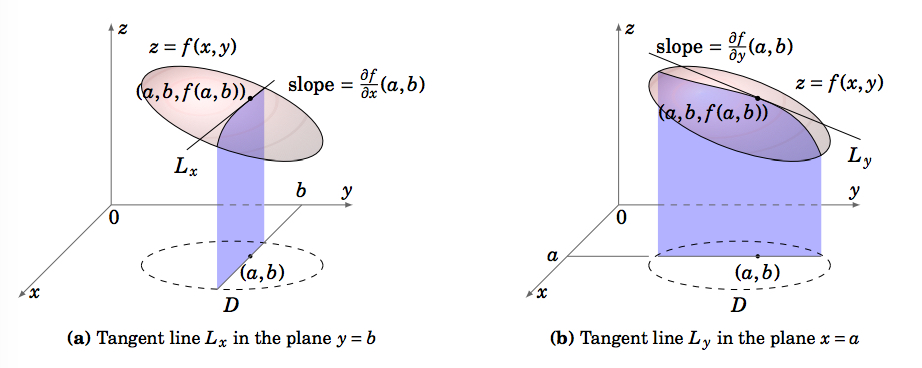
En el apartado anterior mencionamos que las derivadas parciales\(\dfrac{∂f}{∂x}\) y\(\dfrac{∂f}{∂y}\) pueden ser pensadas como la tasa de cambio de una función\(z = f (x, y)\) en las\(y\) direcciones positiva\(x\) y positiva, respectivamente. Recordemos que la derivada\(\dfrac{dy}{dx}\) de una función\(y = f (x)\) tiene un significado geométrico, es decir, como la pendiente de la línea tangente a la gráfica de\(f\) en el punto\((x, f (x))\) en\(\mathbb{R}^2\). Hay un significado geométrico similar a las derivadas parciales\(\dfrac{∂f}{∂x}\) y\(\dfrac{∂f}{∂y}\) de una función\(z = f (x, y)\): dado un punto\((a,b)\) en el dominio\(D\) de\(f (x, y)\), la traza de la superficie descrita por\(z = f (x, y)\) en el plano\(y = b\) es una curva\(\mathbb{R}^ 3\) a través del punto \((a,b, f (a,b))\), y la pendiente de la línea tangente\(L_x\) a esa curva en ese punto es\(\dfrac{∂f}{∂x} (a,b)\). De igual manera,\(\dfrac{∂f}{∂y} (a,b)\) es la pendiente de la línea tangente\(L_y\) a la traza de la superficie\(z = f (x, y)\) en el plano\(x = a\) (ver Figura 2.3.1).
Dado que la derivada\(\dfrac{dy}{dx}\) de una función\(y = f (x)\) se usa para encontrar la línea tangente a la gráfica de\(f\) (que es una curva en\(\mathbb{R}^2\)), podría esperarse que las derivadas parciales se puedan usar para definir un plano tangente a la gráfica de una superficie\(z = f (x, y)\). Esto efectivamente resulta ser el caso. Primero, necesitamos una definición de plano tangente. La idea intuitiva es que un plano tangente “solo toca” una superficie en un punto. La definición formal imita la noción intuitiva de una línea tangente a una curva.
Definición 2.4: Planos tangentes
Dejar\(z = f (x, y)\) ser la ecuación de una superficie\(S\) en\(\mathbb{R}^ 3\), y dejar\(P = (a,b, c)\) ser un punto sobre\(S\). Dejar\(T\) ser un plano que contiene el punto\(P\), y dejar\(Q = (x, y, z)\) representar un punto genérico en la superficie\(S\). Si el ángulo (agudo) entre el vector\(\vec{PQ}\) y el plano\(T\) se acerca a cero a medida que el punto\(Q\) se acerca\(P\) a lo largo de la superficie\(S\), entonces llamamos\(T\) al plano tangente a\(S\) at\(P\).
Obsérvese que dado que dos líneas en\(\mathbb{R}^ 3\) determinan un plano, entonces las dos líneas tangentes a la superficie\(z = f (x, y)\) en las\(y\) direcciones\(x\) y descritas en la Figura 2.3.1 están contenidas en el plano tangente en ese punto, si el plano tangente existe en ese punto. La existencia de esas dos líneas tangentes no garantiza por sí misma la existencia del plano tangente. Es posible que si tomamos la traza de la superficie en el plano\(x − y = 0\) (lo que hace un ángulo de 45◦ con el\(x\) eje positivo), la curva resultante en ese plano pueda tener una línea tangente que no está en el plano determinado por las otras dos líneas tangentes, o puede que no tenga una línea tangente en absoluto en ese punto. Por suerte, resulta que si\(\dfrac{∂f}{∂x}\) y\(\dfrac{∂f}{∂y}\) existen en una región alrededor de un punto\((a,b)\) y son continuos en\((a,b)\) entonces el plano tangente a la superficie\(z = f (x, y)\) existirá en el punto\((a,b, f (a,b))\). En este texto, esas condiciones siempre se mantendrán.
Supongamos que queremos una ecuación del plano tangente\(T\) a la superficie\(z = f (x, y)\) en un punto\((a,b, f (a,b))\). Dejar\(L_x\) y\(L_y\) ser las líneas tangentes a las trazas de la superficie en los planos\(y = b\) y\(x = a\), respectivamente (como en la Figura 2.3.2), y supongamos que las condiciones\(T\) para existir sí se mantienen. Entonces la ecuación para\(T\) es
\[A(x− a)+B(y− b)+C(z − f (a,b)) = 0 \label{Eq2.4}\]
donde\(n = (A,B,C)\) es un vector normal al plano\(T\). Ya que\(T\) contiene las líneas\(L_x\) y\(L_y\), entonces todo lo que necesitamos son vectores\(v_x\) y\(v_y\) que son paralelos a\(L_x \text{and } L_y\), respectivamente, y luego vamos\(n = v_x × v_y\).

Dado que la pendiente de\(L_x\) es\(\dfrac{∂f}{∂x} (a,b)\), entonces el vector\(v_x = (1,0, \dfrac{∂f}{∂x} (a,b))\) es paralelo a\(L_x\) (ya que\(v_x\) se encuentra en el\(xz\) plano -y se encuentra en una línea con pendiente\(\dfrac{\dfrac{∂f}{∂x}(a,b)}{1} = \dfrac{∂f}{∂x} (a,b)\). Ver Figura 2.3.3). Del mismo modo, el vector\(v_y = (0,1, \dfrac{∂f}{∂y} (a,b))\) es paralelo a\(L_y\). De ahí que el vector
\[\textbf{n} = \mathbf{v_x} × \mathbf{v_y} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\[4pt] 1 & 0 & \dfrac{∂f}{∂x}(a,b) \\[4pt] 0 & 1 & \dfrac{∂f}{∂y} (a,b) \end{vmatrix} =-\dfrac{∂f}{∂x}(a,b)\textbf{i}-\dfrac{∂f}{∂y}(a,b)\textbf{j}+\textbf{k} \nonumber \]
es normal a la planta\(T\). Así la ecuación de\(T\) es
\[-\dfrac{∂f}{∂x}(a,b)(x-a)-\dfrac{∂f}{∂y}(a,b)(y-b)+z-f(a,b)=0 \label{Eq2.5}\]
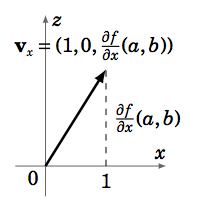
Multiplicando ambos lados por −1, tenemos el siguiente resultado:
La ecuación del plano tangente a la superficie\(z = f (x, y)\) en el punto\((a,b, f (a,b))\) es
\[\dfrac{∂f}{∂x}(a,b)(x-a)+\dfrac{∂f}{∂y}(a,b)(y-b)-z+f(a,b)=0 \label{Eq2.6}\]
Ejemplo 2.13
Encuentra la ecuación del plano tangente a la superficie\(z = x^2 + y^2\) en el punto (1,2,5).
Solución
Para la función\(f (x, y) = x^2 + y^2\), tenemos\(\dfrac{∂f}{∂x} = 2x\) y\(\dfrac{∂f}{∂y} = 2y\), así la ecuación del plano tangente en el punto\((1,2,5)\) es
\[\nonumber 2(1)(x−1)+2(2)(y−2)− z +5 = 0 \text{ , or }\]
\[\nonumber 2x+4y− z −5 = 0\]
De manera similar, se puede demostrar que si una superficie se define implícitamente por una ecuación de la forma\(F(x, y, z) = 0\), entonces el plano tangente a la superficie en un punto\((a,b, c)\) viene dado por la ecuación
\[\dfrac{∂F}{∂x}(a,b, c)(x− a)+ \dfrac{∂F}{∂y}(a,b, c)(y− b)+ \dfrac{∂F}{∂z}(a,b, c)(z − c) = 0 \label{Eq2.7}\]
Tenga en cuenta que la Ecuación\ ref {Eq2.6} es el caso especial de la Ecuación\ ref {Eq2.7} donde\(F(x, y, z) = f (x, y)− z\).
Ejemplo 2.14
Encuentra la ecuación del plano tangente a la superficie\(x^2 + y^2 + z^2 = 9\) en el punto (2,2, −1).
Para la función\(F(x, y, z) = x^2 + y^2 + z^2 −9\), tenemos\(\dfrac{∂F}{∂x} = 2x\),\(\dfrac{∂F}{∂y} = 2y\), y\(\dfrac{∂F}{∂z} = 2z\), así la ecuación del plano tangente en (2,2, −1) es
\[\nonumber 2(2)(x−2)+2(2)(y−2)+2(−1)(z +1) = 0 \text{, or}\]
\[\nonumber 2x+2y− z −9 = 0\]


