2.5: Maxima y Minima
- Page ID
- 111341
El gradiente se puede utilizar para encontrar puntos extremos de funciones de valor real de varias variables, es decir, puntos donde la función tiene un máximo local o mínimo local. Consideraremos solo funciones de dos variables; las funciones de tres o más variables requieren métodos que utilicen álgebra lineal.
Definición 2.7
Dejar\(f (x, y)\) ser una función de valor real, y dejar\((a,b)\) ser un punto en el dominio de\(f\). Decimos que\(f\) tiene un máximo local en\((a,b)\) si\(f (x, y) \le f (a,b)\) para todos\((x, y)\) dentro de algún disco de radio positivo centrado en\((a,b)\), es decir hay algunos suficientemente pequeños\(r > 0\) tales que\(f (x, y) \le f (a,b)\text{ for all }(x, y)\) para los cuales\((x− a)^2 +(y− b)^2 < r^2\).
De igual manera, decimos que\(f\) tiene un mínimo local en el\((a,b)\text{ if }f (x, y) \gt f (a,b)\text{ for all }(x, y)\) interior de algún disco de radio positivo centrado en\((a,b)\).
Si\(f (x, y) \le f (a,b)\text{ for all }(x, y)\) en el dominio de\(f\), entonces\(f\) tiene un máximo global en\((a,b)\). Si\(f (x, y) \ge f (a,b)\text{ for all }(x, y)\text{ in the domain of }f \text{, then }f\) tiene un mínimo global en\((a,b)\).
Supongamos que\((a,b)\) es un punto máximo local para\(f (x, y)\), y que las derivadas parciales de primer orden\(f\) existen en\((a,b)\). Sabemos que\(f (a,b)\) es el mayor valor de\(f (x, y)\text{ as }(x, y)\) va en todas las direcciones desde el punto\((a,b)\), en algún disco suficientemente pequeño centrado en\((a,b)\). En particular,\(f (a,b)\) es el mayor valor de\(f\) en la\(x\) dirección (alrededor del punto\((a,b)\)), es decir, la función de una sola variable\(g(x) = f (x,b)\) tiene un máximo local en\(x = a\). Entonces eso lo sabemos\(g ′ (a) = 0\). Ya que\(g ′ (x) = \dfrac{∂f}{∂x} (x,b)\text{, then }\dfrac{∂f}{∂x} (a,b) = 0\). De igual manera,\(f (a,b)\) es el mayor valor de\(f\) cerca\((a,b)\) en la\(y\) dirección y así\(\dfrac{∂f}{∂y} (a,b) = 0\). Tenemos así el siguiente teorema:
Teorema 2.5
Dejar\(f (x, y)\) ser una función de valor real tal que ambos\(\dfrac{∂f}{∂x} (a,b)\) y\(\dfrac{∂f}{∂y} (a,b)\) existir. Entonces una condición necesaria\(f (x, y)\) para tener un máximo o mínimo local en\((a,b)\) es esa\(\nabla f (a,b) = \textbf{0}\).
Nota: El teorema 2.5 se puede extender para aplicarlo a funciones de tres o más variables.
Un punto\((a,b)\) donde\(\nabla f (a,b) = \textbf{0}\) se denomina punto crítico para la función\(f (x, y)\). Entonces dada una función\(f (x, y)\), para encontrar los puntos críticos de\(f\) usted tiene que resolver las ecuaciones\(\dfrac{∂f}{∂x} (x, y) = 0\text{ and }\dfrac{∂f}{∂y} (x, y) = 0\) simultáneamente para\((x, y)\). Similar al caso de una sola variable, la condición necesaria que no siempre\(\nabla f (a,b) = \textbf{0}\) es suficiente para garantizar que un punto crítico sea un máximo o mínimo local.
Ejemplo 2.18
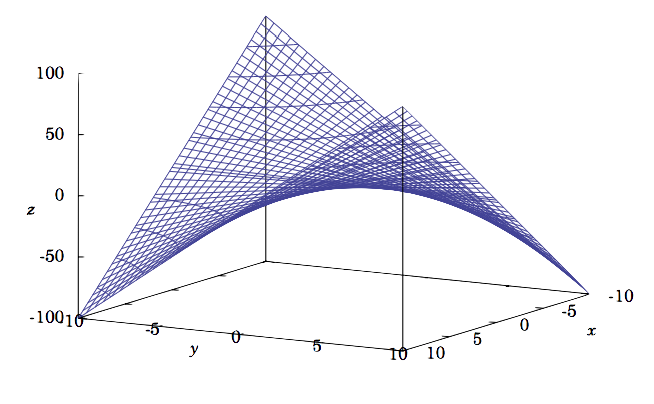
La función\(f (x, y) = x y\) tiene un punto crítico en\((0,0)\):\(\dfrac{∂f}{∂x} = y = 0 \Rightarrow y = 0\), y\(\dfrac{∂f}{∂y} = x = 0 \Rightarrow x = 0\), así\((0,0)\) es el único punto crítico. Pero claramente\(f\) no tiene un máximo o mínimo local en\((0,0)\) ya que cualquier disco alrededor\((0,0)\) contiene puntos\((x, y)\) donde los valores de\(x\) y\(y\) tienen el mismo signo (así que eso\(f (x, y) = x y \gt 0 = f (0,0))\) y diferentes signos (así que eso\(f (x, y) = x y < 0 = f (0,0))\). De hecho, a lo largo del camino\(y = x\) en\(\mathbb{R}^2\)\(f (x, y) = x^2\),, que tiene un mínimo local en\((0,0)\), mientras que a lo largo del camino\(y = −x\) tenemos\(f (x, y) = −x^2\), que tiene un máximo local en\((0,0)\). Así\((0,0)\) es un ejemplo de un punto de silla de montar, es decir, es un máximo local en una dirección y un mínimo local en otra dirección. El gráfico de\(f (x, y)\) se muestra en la Figura 2.5.1, que es un paraboloide hiperbólico.
El siguiente teorema da condiciones suficientes para que un punto crítico sea un máximo o mínimo local de una función suave (es decir, una función cuyas derivadas parciales de todos los órdenes existen y son continuas), lo que no probaremos aquí.
Teorema 2.6
Dejar\(f (x, y)\) ser una función fluida de valor real, con un punto crítico en\((a,b)\) (es decir\(\nabla f (a,b) = 0\)). Definir
\[\nonumber D = \dfrac{∂^2 f}{∂x^2} (a,b) \dfrac{∂^2 f}{∂y^2}(a,b)− \left (\dfrac{∂^2 f}{∂y∂x} (a,b)\right )^2\]
Entonces
- si\(D > 0 \text{ and }\dfrac{∂^2 f}{∂x^2} (a,b) > 0\), entonces\(f\) tiene un mínimo local en\((a,b)\)
- si\(D > 0 \text{ and }\dfrac{∂^2 f}{∂x^2} (a,b) < 0\), entonces\(f\) tiene un máximo local en\((a,b)\)
- si no\(D < 0 \text{, then }f\) tiene un mínimo local ni un máximo local en\((a,b)\)
- si\(D = 0\), entonces la prueba falla
Si la condición (c) se mantiene, entonces\((a,b)\) es un punto de sillín. Tenga en cuenta que la suposición de que\(f (x, y)\) es suave significa que
\[ D = \begin{vmatrix} \dfrac{∂^2 f}{∂x^2} (a,b) & \dfrac{∂^2 f}{∂y∂x} (a,b) \\[4pt] \dfrac{∂^2 f}{∂x∂y} (a,b) & \dfrac{∂^2 f}{∂y^2} (a,b) \\[4pt] \end{vmatrix}\]
ya que\(\dfrac{∂^2 f}{∂y∂x} = \dfrac{∂^2 f}{∂x∂y}\). También, si\(D > 0\) entonces\(\dfrac{∂^2 f}{∂x^2} (a,b) \dfrac{∂^2 f}{∂y^2} (a,b) = D + \left ( \dfrac{∂^2 f}{∂y∂x} (a,b)\right )^2 > 0\), y así\(\dfrac{∂^2 f}{∂x^2} (a,b)\text{ and }\dfrac{∂^2 f}{∂y^2} (a,b)\) tienen el mismo signo. Esto significa que en las partes (a) y (b) del teorema se puede sustituir\(\dfrac{∂^2 f}{∂x^2} (a,b)\) por\(\dfrac{∂^2 f}{∂y^2} (a,b)\) si se desea.
Ejemplo 2.19
Encuentra todos los máximos y mínimos locales de\(f (x, y) = x^2 + x y+ y^2 −3x\).
Solución
Primero encuentra los puntos críticos, es decir, dónde\(\nabla f = \textbf{0}\). Desde
\[\nonumber \dfrac{∂f}{∂x} = 2x+ y−3 \text{ and }\dfrac{∂f}{∂y} = x+2y\]
entonces los puntos críticos\((x, y)\) son las soluciones comunes de las ecuaciones
\[\nonumber \begin{align} 2x+ y−3 &= 0 \\[4pt] \nonumber x +2y &= 0 \end{align}\]
que tiene la solución única\((x, y) = (2,−1)\). Entonces (2, −1) es el único punto crítico.
Para usar el Teorema 2.6, necesitamos las derivadas parciales de segundo orden:
\[\nonumber \dfrac{∂^2 f}{∂x^2} = 2 ,\quad \dfrac{∂^2 f}{∂y^2} = 2 ,\quad \dfrac{∂^2 f}{∂y∂x} = 1\]
y así
\[\nonumber D = \dfrac{∂^2 f}{∂x^2} (2,−1) \dfrac{∂^2 f}{∂y^2} (2,−1)− \left ( \dfrac{∂^2 f}{∂y∂x} (2,−1)\right )^2 = (2)(2)−1^2 = 3 > 0\]
y\(\dfrac{∂^2 f}{∂x^2} (2,−1) = 2 > 0\). Así, (2, −1) es un mínimo local.
Ejemplo 2.20
Encuentra todos los máximos y mínimos locales de\(f (x, y) = x y− x^3 − y^2\).
Solución
Primero encuentra los puntos críticos, es decir, dónde\(\nabla f = \textbf{0}\). Desde
\[\nonumber \dfrac{∂f}{∂x} = y−3x^2 \text{ and }\dfrac{∂f}{∂y} = x−2y\]
entonces los puntos críticos\((x, y)\) son las soluciones comunes de las ecuaciones
\[\nonumber \begin{align} y−3x^2 &= 0 \\[4pt] \nonumber x−2y &= 0 \end{align}\]
La primera ecuación rinde\(y = 3x^2\), sustituyendo eso en los rendimientos de la segunda ecuación\(x−6x^2 = 0\), que tiene las soluciones\(x = 0 \text{ and }x = \dfrac{1}{6}\). Entonces\(x = 0 \Rightarrow y = 3(0) = 0 \text{ and }x = \dfrac{1}{6} \Rightarrow y = 3 \left (\dfrac{1}{6} \right )^2 = \dfrac{1}{12}\). Entonces los puntos críticos son\((x, y) = (0,0)\) y\((x, y) = \left ( \dfrac{1}{6} , \dfrac{1}{12} \right )\).
Para usar el Teorema 2.6, necesitamos las derivadas parciales de segundo orden:
\[\nonumber \dfrac{∂^2 f}{∂x^2} = −6x ,\quad \dfrac{∂^2 f}{∂y^2} = −2 ,\quad \dfrac{∂^2 f}{∂y∂x} = 1\]
Entonces
\[\nonumber D = \dfrac{∂^2 f}{∂x^2} (0,0) \dfrac{∂^2 f}{∂y^2} (0,0)− \left (\dfrac{∂^2 f}{∂y∂x} (0,0)\right )^2 = (−6(0))(−2)−1^2 = −1 < 0\]
y así\((0,0)\) es una punta de silla de montar. También,
\[\nonumber D = \dfrac{∂^2 f}{∂x^2} \left ( \dfrac{1}{6} ,\dfrac{1}{12 } \right ) \dfrac{∂^2 f}{∂y^2} \left (\dfrac{1}{6} , \dfrac{1}{12}\right ) − \left (\dfrac{∂^2 f}{∂y∂x} \left ( \dfrac{1}{6} , \dfrac{1}{12}\right ) \right)^2 = (−6 \left (\dfrac{1}{6}\right )) (−2)−1^2 = 1 > 0\]
y\(\dfrac{∂^2 f}{∂x^2}\left (\dfrac{1}{6} , \dfrac{1}{12} \right ) = −1 < 0\). Así,\(\left (\dfrac{1}{6} , \dfrac{1}{12}\right )\) es un máximo local.
Ejemplo 2.21
Encuentra todos los máximos y mínimos locales de\(f (x, y) = (x−2)^4 +(x−2y)^2\).
Primero encuentra los puntos críticos, es decir, dónde\(\nabla f = \textbf{0}\). Desde
\[\nonumber \dfrac{∂f}{∂x} = 4(x−2)^3 +2(x−2y) \text{ and }\dfrac{∂f}{∂y} = −4(x−2y)\]
entonces los puntos críticos\((x, y)\) son las soluciones comunes de las ecuaciones
\[\nonumber \begin{align} 4(x−2)^3 +2(x−2y) &= 0 \\[4pt] \nonumber −4(x−2y) &= 0 \end{align}\]
La segunda ecuación rinde\(x = 2y\), sustituyendo eso en los rendimientos de la primera ecuación\(4(2y−2)^3 = 0\), que tiene la solución\(y = 1\), y así\(x = 2(1) = 2\). Así,\((2,1)\) es el único punto crítico.
Para usar el Teorema 2.6, necesitamos las derivadas parciales de segundo orden:
\[\nonumber \dfrac{∂^2 f}{∂x^2} = 12(x−2)^2 +2,\quad \dfrac{∂^2 f}{∂y^2} = 8 ,\quad \dfrac{∂^2 f}{∂y∂x} = −4\]
Entonces
\[\nonumber D = \dfrac{∂^2 f}{∂x^2} (2,1) \dfrac{∂^2 f}{∂y^2} (2,1)− \left (\dfrac{∂^2 f}{∂y∂x} (2,1)\right )^2 = (2)(8)−(−4)^2 = 0\]
y así la prueba falla. ¿Qué se puede hacer ante esta situación? En ocasiones es posible examinar la función para ver directamente la naturaleza de un punto crítico. En nuestro caso, vemos eso\(f (x, y) \ge 0\) para todos\((x, y)\), ya que\(f (x, y)\) es la suma de las potencias cuarta y segunda de los números y por lo tanto debe ser no negativa. Pero también vemos eso\(f (2,1) = 0\). Así\(f (x, y) \ge 0 = f (2,1)\) para todos\((x, y)\), y por lo tanto\((2,1)\) es de hecho un mínimo global para\(f\).
Ejemplo 2.22
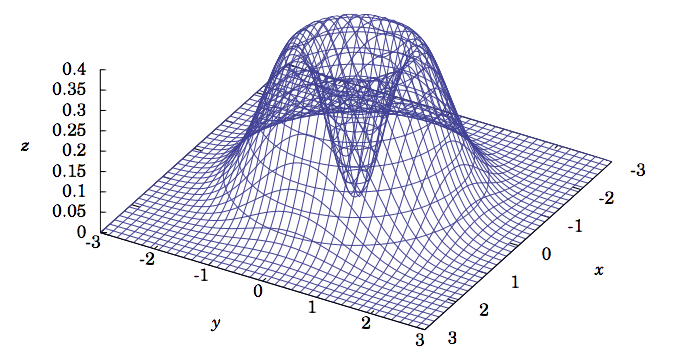
Encuentra todos los máximos y mínimos locales de\(f (x, y) = (x^2 + y^2 )e^{−(x^2+y^2)}\).
Solución
Primero encuentra los puntos críticos, es decir, dónde\(\nabla f = 0\). Desde
\[\nonumber \begin{align} \dfrac{∂f}{∂x} &= 2x(1−(x^2 + y^2 ))e^{−(x^2+y^2)} \\[4pt] \nonumber \dfrac{∂f}{∂y} &= 2y(1−(x^2 + y^2))e^{−(x^2+y^2)} \end{align}\]
entonces los puntos críticos son\((0,0)\) y todos los puntos\((x, y)\) en el círculo unitario\(x^2 + y^2 = 1\).
Para usar el Teorema 2.6, necesitamos las derivadas parciales de segundo orden:
\[\nonumber \begin{align} \dfrac{∂^2 f}{∂x^2} &= 2[1−(x^2 + y^2 )−2x^2 −2x^2 (1−(x^2 + y^2))]e^{−(x^2+y^2)} \\[4pt] \nonumber \dfrac{∂^2 f}{∂y^2} &= 2[1−(x^2 + y^2 )−2y^2 −2y^2 (1−(x^2 + y^2))]e^{−(x^2+y^2)} \\[4pt] \nonumber \dfrac{∂^2 f}{∂y∂x} &= −4x y[2−(x^2 + y^2 )]e^{−(x^2+y^2)} \end{align}\]
En\((0,0)\), tenemos\(D = 4 > 0\) y\(\dfrac{∂^2 f}{∂x^2} (0,0) = 2 > 0\), así\((0,0)\) es un mínimo local. Sin embargo, para los puntos\((x, y)\) en el círculo unitario\(x^2 + y^2 = 1\), tenemos
\[\nonumber D = (−4x^2 e^{−1} )(−4y^2 e^{−1} )−(−4x ye^{−1} )^2 = 0\]
y así la prueba falla. Si miramos la gráfica de\(f (x, y)\), como se muestra en la Figura 2.5.2, parece que podríamos tener un máximo local para\((x, y)\) en el círculo unitario\(x^2 + y^2 = 1\). Si cambiamos a usar coordenadas polares en\((r,\theta )\) lugar de\((x, y)\) in\(\mathbb{R}^2\)\(r^2 = x^2+y^2\), donde, entonces vemos que podemos escribir\(f (x, y)\)\(r\) solo en función\(g(r)\) de la variable:\(g(r) = r^2 e^{−r^2}\). Entonces\(g ′ (r) = 2r(1 − r^2 )e^{−r^2}\), por lo que tiene un punto crítico en\(r = 1\), y podemos comprobarlo\(g′′(1) = −4e^{−1} < 0\), por lo que la Prueba de Segunda Derivada del cálculo de una sola variable dice que\(r = 1\) es un máximo local. Pero\(r = 1\) corresponde al círculo unitario\(x^2 + y^2 = 1\). Así, los puntos\((x, y)\) en el círculo unitario\(x^2 + y^2 = 1\) son puntos máximos locales para\(f\).
