6.3: Extrema y Modelos

Última actualización
Guardar como PDF

Page ID: 110823

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En la última sección, se utilizó el comportamiento final y ceros para bosquejar la gráfica de un polinomio dado. También mencionamos que se necesita un semestre de cálculo para aprender una técnica analítica utilizada para calcular los “puntos de inflexión” del polinomio. Dicho esto, seguiremos persiguiendo las coordenadas de los “puntos de inflexión” en esta sección, pero usaremos la calculadora gráfica para asistirnos en esta búsqueda; y luego usaremos esta técnica con algunas aplicaciones.

Extrema

Antes de comenzar, primero nos gustaría diferenciar entre los extremos locales y los extremos absolutos. Esto se logra mejor por medio de un ejemplo. Considere, si se quiere, las gráficas de tres funciones polinómicas en la Figura 1.

En la primera figura, Figura$\PageIndex{1a}$, el punto A es el punto más bajo “absoluto” de la gráfica. Por lo tanto, el valor y del punto A es un valor mínimo absoluto de la función.

En la segunda figura, Figura$\PageIndex{1b}$, no hay un punto más alto “absoluto” en la gráfica (la gráfica sube al infinito positivo), ni hay un punto más bajo “absoluto” en la gráfica (la gráfica baja al infinito negativo). Por lo tanto, esta función no tiene ni un mínimo absoluto ni un máximo absoluto.

Sin embargo, el punto B de la Figura$\PageIndex{1b}$ es el punto más alto en su vecindad inmediata. Si vaga demasiado hacia la derecha, hay puntos en la gráfica más altos que el punto B, pero localmente el punto B es el punto más alto. Por lo tanto, el valor y del punto B se denomina valor máximo local de la función.

De igual manera, el punto C de la Figura$\PageIndex{1b}$ es el punto más bajo en su vecindad inmediata. Si vagas demasiado hacia la izquierda, hay puntos en la gráfica más bajos que el punto C, pero, en su vecindad, el punto C es el punto más bajo. Por lo tanto, el valor y del punto C se denomina mínimo local de la función.

Figura$\PageIndex{1}$: Diferenciar entre extremos locales y absolutos.

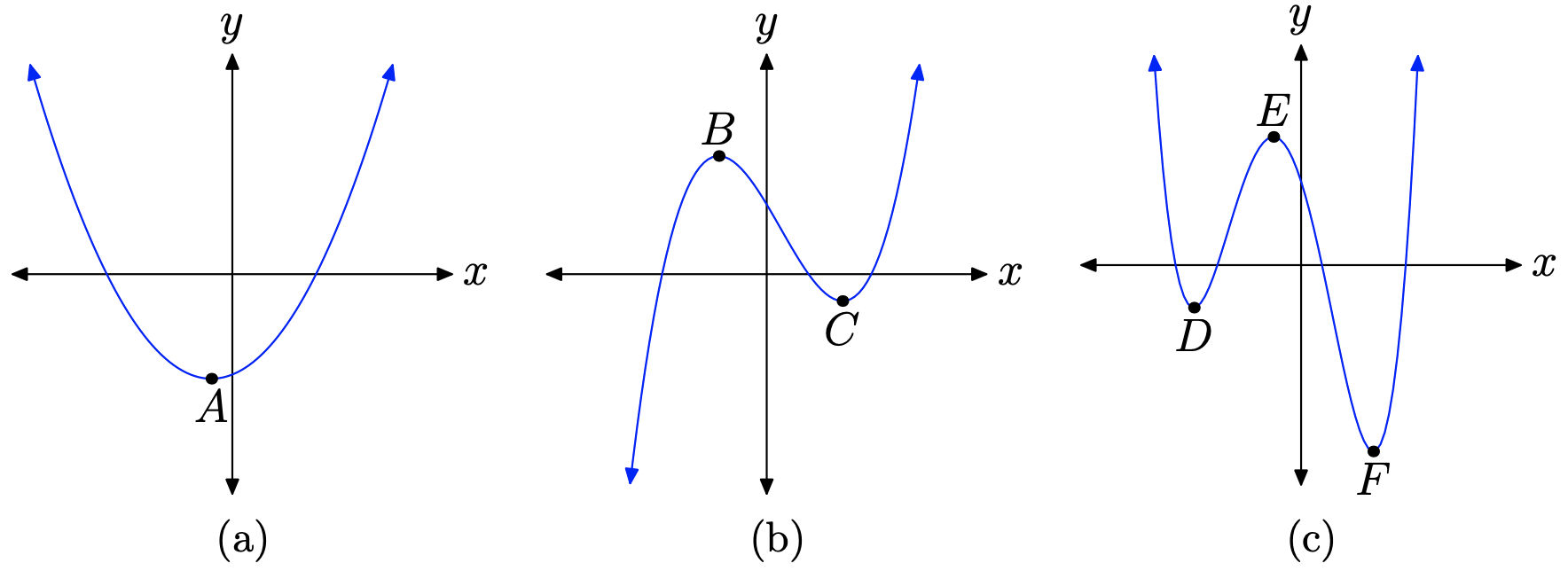
Por último, eche un vistazo a la gráfica de la Figura$\PageIndex{1c}$. El punto F es el punto más bajo “absoluto” de la gráfica, por lo que el valor y del punto F es un mínimo absoluto de la función. Por otro lado, no hay punto más alto en la gráfica de la Figura$\PageIndex{1}$ (c), ya que cada extremo de la gráfica escapa al infinito positivo. De ahí que la función no tenga un máximo absoluto.

Localmente, el punto D en la Figura$\PageIndex{1}$ (c) es el punto más bajo, por lo que el valor y del punto D es un mínimo local de la función. De igual manera, en su vecindad inmediata, el punto E es el punto más alto, por lo que el valor y del punto E es un máximo local.

Presentamos ahora las definiciones formales.

Definición: Máximo Absoluto

Supongamos que$c$ está en el dominio de una función$f$ y$f(c) \geq f(x)$ para todos$x$ en el dominio de$f$. Entonces decimos que$f(c)$ es un máximo absoluto de la función$f$. Del mismo modo, si$f(c) \leq f(x)$ para todos$x$ en el dominio de$f$, entonces$f(c)$ es un mínimo absoluto de la función$f$.

La definición de extremo local es menos restrictiva.

Definición: Máximo local

Que c esté en el dominio de$f$. Si$f(c) \geq f(x)$ para todos$x$ en un barrio que contiene c, entonces decimos que f (c) es un máximo local de la función f. por otro lado, si$f(c) \leq f(x)$ para todos$x$ en un barrio que contiene$c$, entonces decimos que f (c) es un mínimo local de la función f.

Cuando los matemáticos dicen “un barrio que contiene”$c$, suelen significar un pequeño intervalo abierto$(a, b)$ que contiene$c$.

Exploremos el uso de la calculadora gráfica para encontrar extremos.

Ejemplo$\PageIndex{1}$

Considerar la función polinómica definida por la ecuación

\[p(x)=2(x-6)(x+2)(x+4). \nonumber\]

Utilice la calculadora gráfica para ayudar a encontrar y clasificar todos los extremos de esta función.

Solución

Primero, ¿cuánto de la gráfica puedes dibujar sin el uso de una calculadora? Los factores lineales de$p(x)$ son x − 6, x + 2 y x + 4, por lo que los ceros son 6, −2 y −4, respectivamente. Entonces ahora sabemos donde la gráfica de p (x) cruza el eje x.

Para determinar el comportamiento final de$p(x)$, necesitamos determinar el término principal. No es necesario expandir completamente el polinomio con la propiedad distributiva.3 Un poco de pensamiento rápidamente revela que si hiciéramos precisamente eso, el término principal en este caso sería$2x^{3}$. En consecuencia, a medida que barremos nuestros ojos de izquierda a derecha, el comportamiento final del polinomio debe coincidir con el de su término principal$2x^{3}$, elevándose desde el infinito negativo, moviéndose a través de sus intercepciones x, luego elevándose al infinito positivo. La única opción es una gráfica similar a la de la Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: La gráfica de$p(x) = 2(x− 6)(x + 2)(x + 4)$ subidas desde el infinito negativo, se mueve a través de sus intercepciones x, luego continúa elevándose hasta el infinito positivo.

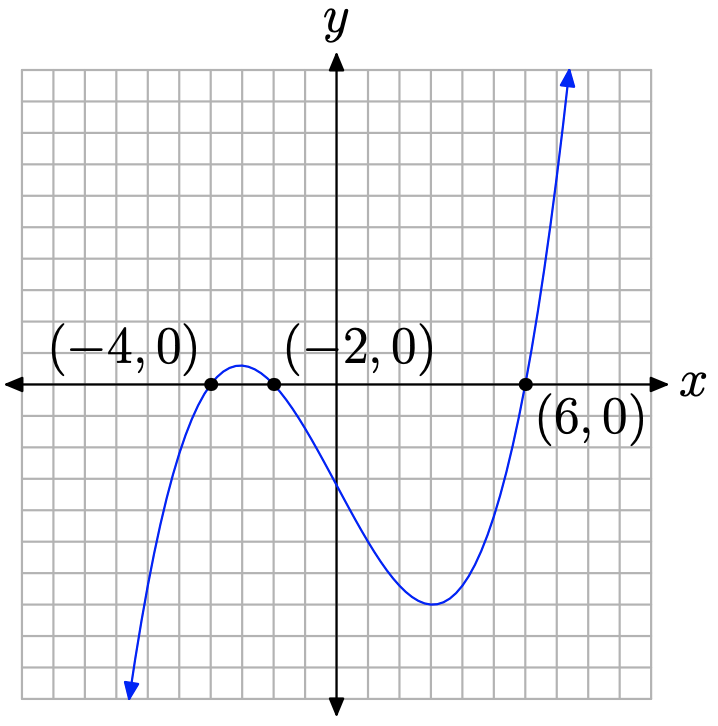
Tenga en cuenta que la gráfica alcanza un máximo local en algún lugar cercano a x = −3 y un mínimo local en aproximadamente x = 3. Podemos encontrar mejores aproximaciones de los extremos locales utilizando las utilidades máximas y mínimas en el menú CALC de la calculadora gráfica.

Primero, graficar la gráfica del polinomio p (x) = 2 (x − 6) (x + 2) (x + 4), como se muestra en la Figura$\PageIndex{3}$ (a), utilizando los parámetros de ventana mostrados en la Figura$\PageIndex{3}$ (b).
Abra el menú CALCULAR presionando 2do CALC. Esto revela un menú de opciones como se muestra en la Figura$\PageIndex{3}$ (c). Para iniciar la utilidad para ayudar a encontrar el máximo local cerca de x = −3 (ver Figura$\PageIndex{2}$), presione 4:maximum en el menú.
La utilidad responde pidiendo un “Left Bound”. Utilice las teclas de flecha para mover el cursor ligeramente a la izquierda del máximo local cerca de x = −3, como se muestra en la Figura$\PageIndex{3}$ (d), luego presione la tecla ENTRAR.

Figura$\PageIndex{3}$. Usando la calculadora gráfica para determinar el máximo local.

La utilidad responde pidiendo un “Encuadernado a la derecha”. Use las teclas de flecha para mover el cursor ligeramente a la derecha del máximo local cerca de x = −3, como se muestra en la Figura$\PageIndex{4}$ (e), luego presione la tecla ENTRAR.
La utilidad responde pidiendo un “Guess”. Mueve el cursor para que quede entre el “Izquierdo Bound” y “Right Bound” hecho anteriormente, como se muestra en la Figura$\PageIndex{4}$ (f), luego presione la tecla ENTRAR. En cualquier lugar entre el límite izquierdo y el borde derecho (las marcas de nota en la parte superior de la pantalla en la Figura$\PageIndex{4}$ (f)) servirán.

Figura$\PageIndex{4}$. Usando la calculadora gráfica para determinar el máximo local (continuación).

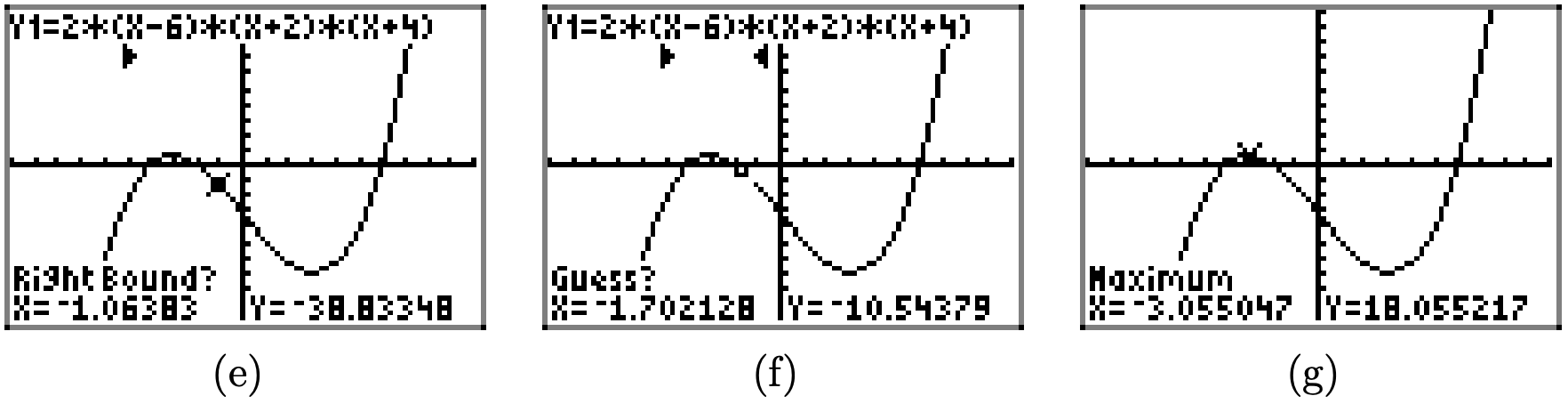
La calculadora responde colocando el cursor en el punto donde se produce el máximo local e informa sus coordenadas en la parte inferior de la pantalla, como se muestra en la Figura$\PageIndex{4}$ (g).

Las coordenadas del punto donde se produce el máximo local son aproximadamente\[(-3.055047,18.055217)\]

Decimos que la función alcanza un valor máximo local de 18.055217 y ese máximo ocurre en$x \approx-3.055047$.

De manera similar, se puede utilizar la utilidad mínima en el menú CALC para encontrar el mínimo local que ocurre cerca de x = 3, como se muestra en la Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$. Utilice la utilidad mínima para encontrar el mínimo local.

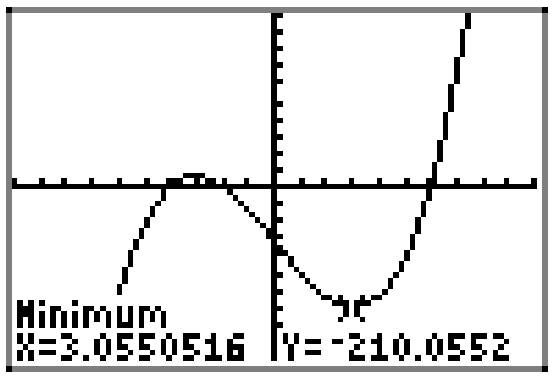
Las coordenadas del punto donde se produce el mínimo local son aproximadamente\[(3.0550516,-210.0552)\]

Decimos que la función alcanza un valor mínimo local de −210.0552 y ese mínimo ocurre en$x \approx 3.0550516$.

Aplicaciones

En esta sección veremos algunas aplicaciones que son modeladas por polinomios.

Ejemplo$\PageIndex{2}$

Una pieza cuadrada de cartón mide 24 pulgadas por lado. John corta cuatro cuadrados más pequeños de cada esquina del cartón, arrojando el material a un lado. Luego dobla los lados del cartón restante para formar una caja abierta sin tapa. Encuentra las dimensiones de los cuadrados cortados de cada esquina de la pieza de cartón original para que John maximice el volumen resultante de la caja.

Solución

Dejar x representar la longitud del lado del corte cuadrado de cada esquina del cuadrado mayor (ver Figura$\PageIndex{6}$ (a)). Debido a que cada lado del cuadrado original mide 24 pulgadas, y estamos cortando dos longitudes de x pulgadas de cada extremo, el largo y ancho resultantes de la caja es de 24 − 2x pulgadas (ver Figura$\PageIndex{6}$ (a) y/o (b)). Cuando tiramos las esquinas cuadradas, luego plegamos los lados, obtenemos una caja con las dimensiones que se muestran en la Figura$\PageIndex{6}$ (b).

Figura$\PageIndex{6}$: Material y caja resultante.

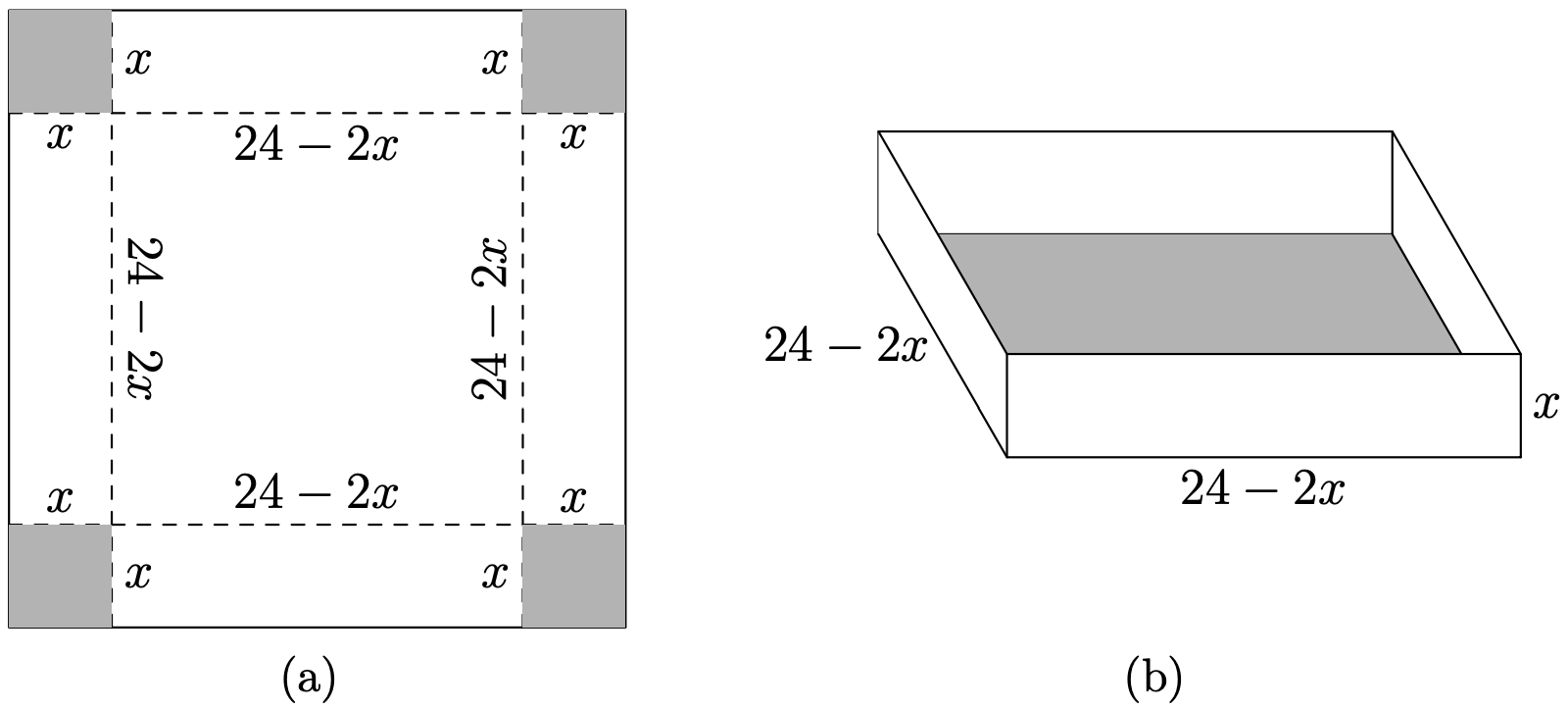
Debido a que el volumen de una caja se calcula tomando el producto del largo y ancho de la base, multiplicado por la altura de la caja, el volumen de la caja viene dado por la fórmula

\[V=x(24-2 x)(24-2 x) \nonumber\]

Podemos simplificar un poco la ecuación (6). Tome un factor de 2 de cada factor de 24−2x, como en

\[V=x(2)(12-x)(2)(12-x) \nonumber\]

luego combinar factores para escribir

\[V=4 x(12-x)^{2} \nonumber\]

Vemos eso$x$ y$12 − x$ son factores lineales de$V$. De ahí que los ceros de V sean 0 y 12, respectivamente. Debido a que 12−x se usa como factor dos veces, 2 es una “raíz doble”, por lo que la gráfica debe ser tangente al eje x en$x = 2$.

Si tuviéramos que expandir completamente la Ecuación (7), obtendríamos un polinomio con término principal$4x^{3}$. Por lo tanto, el comportamiento final de nuestro polinomio de volumen debe coincidir con el comportamiento final de su término principal, elevándose desde el infinito negativo, moviéndose a través de ceros, luego subiendo al infinito positivo. No obstante, debido a que tenemos una “doble raíz” en x = 2, esperamos que la gráfica “bese” el eje horizontal en este cero en lugar de pasar por este cero.

Así, la única forma posible que puede asumir el polinomio volumétrico es la que se muestra en la Figura$\PageIndex{7}$.

Figura$\PageIndex{7}$: El volumen de la caja en función de la longitud del borde de los cuadrados eliminados.

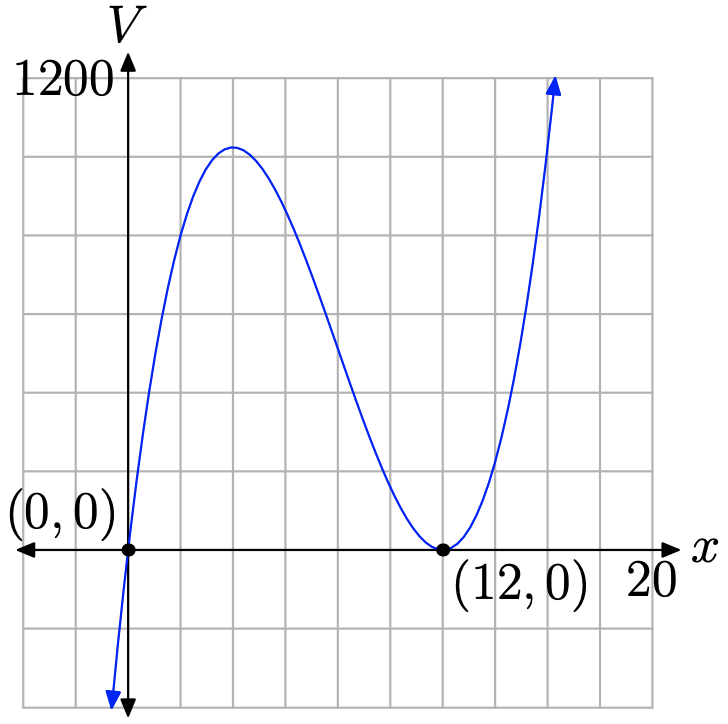
El dominio del polinomio definido por la ecuación (7) es el conjunto de todos los números reales, o, en notación de intervalos,$(-\infty, \infty)$. En Figura$\PageIndex{7}$, si proyectas todos los puntos de la gráfica sobre el eje x, todo el eje x estaría sombreado, indicando además que el dominio de la función de volumen son todos números reales.

Sin embargo, este dominio matemático$(-\infty, \infty)$ ignora el hecho de que x representa la longitud del corte cuadrado de cada esquina del cuadrado original de cartón (ver Figura$\PageIndex{6}$ (a)). No se puede cortar un cuadrado que tenga un lado de longitud negativa. Tras una inspección adicional, el cuadrado más grande que podría cortarse de cada esquina tendría un borde de 12 pulgadas. Recuerda, tienes que cortar cuatro cuadrados, uno de cada esquina, y el borde de la pieza cuadrada original de cartón mide apenas 24 pulgadas. Así, el problema constriñe x al intervalo [0, 12]. Este dominio se llama el dominio empírico, o, si se quiere, el dominio práctico.

Definición: Dominio empírico

El dominio empírico de una función es un subconjunto del dominio matemático, restringido para satisfacer las restricciones del modelo.

Así, solo una porción de la gráfica de la Figura tiene$\PageIndex{7}$ sentido para esta aplicación, la parte que se dibuja sobre el dominio empírico [0, 12], como se muestra en la Figura$\PageIndex{8}$.

Figura$\PageIndex{8}$: Esbozo de la función de volumen sobre el dominio empírico [0, 12].

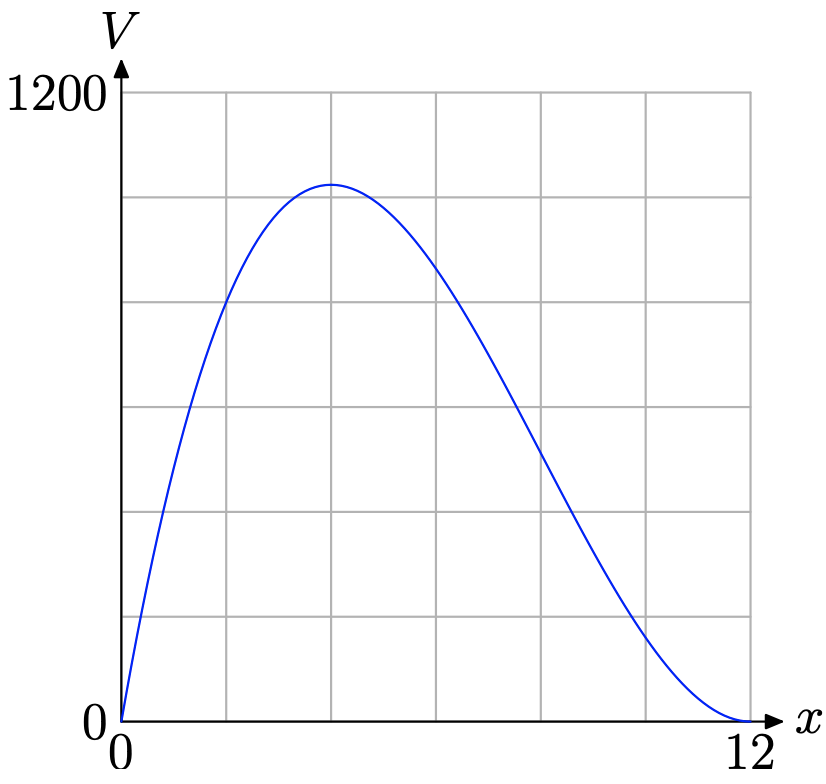
Recuerda, el objetivo original era encontrar el valor de x que maximizara el volumen de la caja. Un rápido vistazo a la gráfica de la Figura$\PageIndex{8}$ muestra que hay un máximo absoluto (al menos en el dominio empírico [0, 12]) cerca de x = 4. Para obtener una mejor aproximación, utilice la utilidad máxima en el menú CALC de su calculadora, como hicimos nosotros para obtener la aproximación que se muestra en la Figura$\PageIndex{9}$ (b).

Figura$\PageIndex{9}$. Encontrar la longitud del borde que maximiza el volumen de la caja.

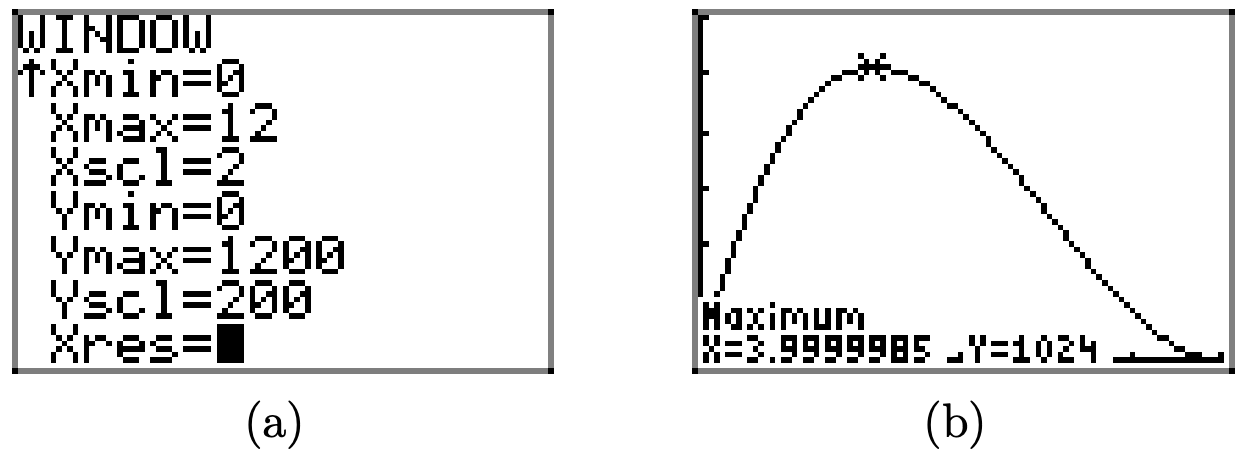
En efecto, parecería que se alcanza un volumen máximo de 1024 pulgadas cúbicas ($V=1024 \mathrm{in}^{3}$) en$x \approx 3.9999985$. Probablemente sea seguro decir que el volumen máximo ocurre si se cortan cuadrados que tienen lados de longitud de 4 pulgadas de las esquinas de la pieza de cartón original. El 3.9999985 probablemente contiene un poco de error debido al error de redondeo en la calculadora. En efecto, es muy probable que algunos lectores obtengan exactamente x = 4 cuando utilicen la utilidad máxima, dependiendo de los límites y la suposición inicial utilizada, así que no se preocupe si la aproximación de su calculadora difiere ligeramente de la nuestra.

Veamos otro ejemplo.

Ejemplo$\PageIndex{3}$

Encuentra las dimensiones del rectángulo de mayor área que tiene su base en el eje x y sus otros dos vértices por encima del eje x y acostado en la gráfica de la parábola$y=4-x^{2}$.

Solución

La gráfica de$y=4-x^{2}$ es una parábola que se abre hacia abajo y se desplaza hacia arriba 4 unidades. El lado derecho de esta ecuación factores

\[y=(2+x)(2-x) \nonumber\]

así que los ceros de esta función son −2 y 2. Debido a que el rectángulo tiene su base en el eje x y sus otros vértices están en la parábola que se encuentra por encima del eje x, solo necesitamos bosquejar la parábola en el dominio [−2, 2] (ver Figura$\PageIndex{10}$).

Figura$\PageIndex{10}$: Rectángulo inscrito bajo una parábola.

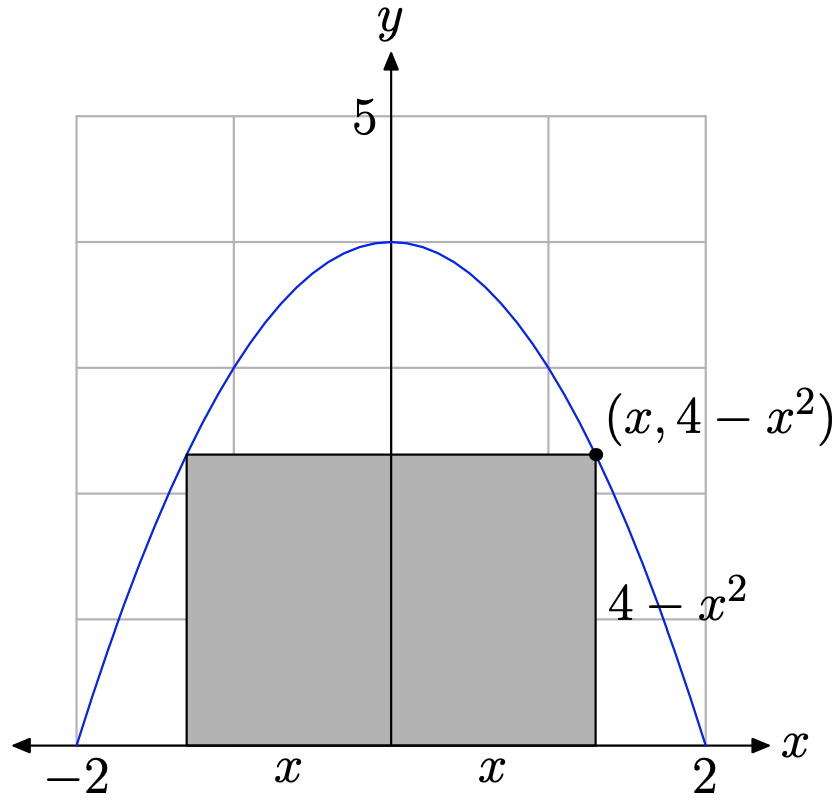
Debido a la simetría, podemos restringir x al dominio empírico [0, 2]. En Figura$\PageIndex{10}$, tenga en cuenta que hemos seleccionado un valor de x de [0, 2], luego trazamos el punto que tiene este valor x en la parábola. Por supuesto, el valor y de este punto lo es$y=4-x^{2}$. Así, la altura del rectángulo es$4-x^{2}$ y la base (o ancho) del rectángulo es dos veces x, o 2x. El área del rectángulo viene dada por

\[A=\text { width } \cdot \text { height }\]

De ahí que el área A en función de x viene dada por el polinomio

\[A=2 x\left(4-x^{2}\right)\]

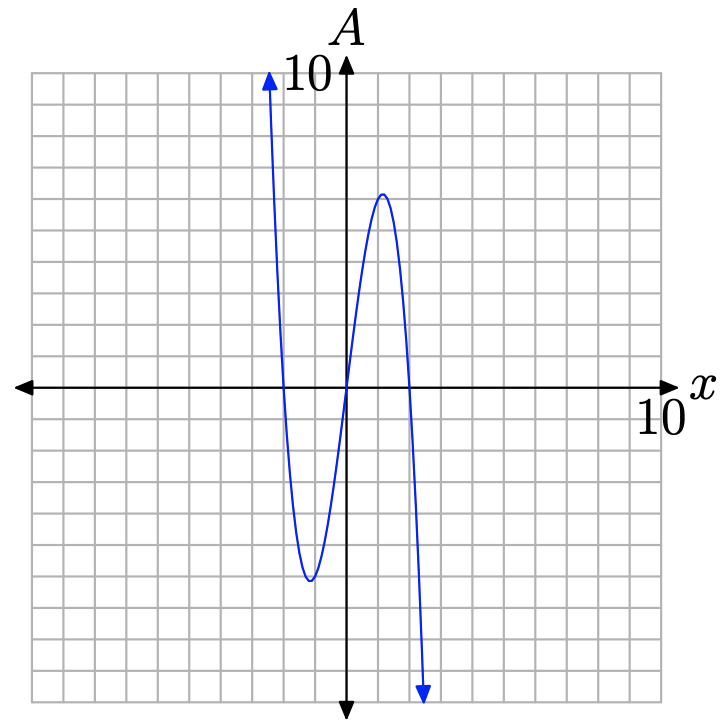
Obsérvese que la ecuación (10) es un polinomio de tercer grado que tiene término principal$-2 x^{3}$. Así, la gráfica del polinomio, al barrer los ojos de izquierda a derecha, debe caer desde el infinito positivo, moverse a través de sus intercepciones x, luego continuar cayendo al infinito negativo.

Podemos facturar la ecuación (10) para obtener

\[A=2 x(2+x)(2-x)\]

Por lo tanto, los ceros del polinomio son 0, −2 y 2, respectivamente. Así, el polinomio debe tener una forma similar a la que se muestra en la Figura$\PageIndex{11}$. Tenga en cuenta que la gráfica tiene intercepciones x en (−2, 0), (0, 0) y (2, 0).

Debido a la naturaleza práctica de este problema, necesitamos restringir x al dominio empírico [0, 2], como se discutió anteriormente (ver Figura$\PageIndex{10}$. La gráfica de A = 2x (2 + x) (2 − x), restringida al dominio [0, 2], se muestra en la Figura$\PageIndex{12}$.

Figura$\PageIndex{12}$. El gráfico del polinomio A = 2x (2 + x) (2 − x) restringido al dominio empírico [0, 2].

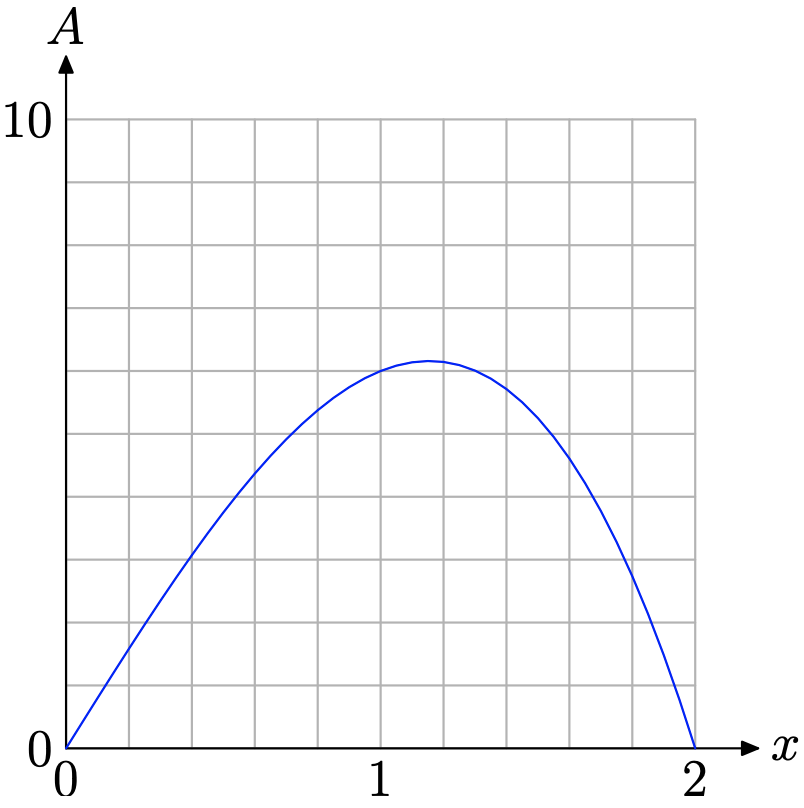
Parece (ver Figura$\PageIndex{12}$) que A alcanza un máximo absoluto (al menos en el dominio empírico [0, 2]) cercano$x \approx 1.2$. Para obtener una mejor aproximación, utilice la utilidad máxima en el menú CALC de la calculadora gráfica, como hicimos para obtener la aproximación que se muestra en la Figura$\PageIndex{13}$ (b).

Figura$\PageIndex{13}$. Utilice la utilidad máxima para obtener una aproximación del valor máximo de A.

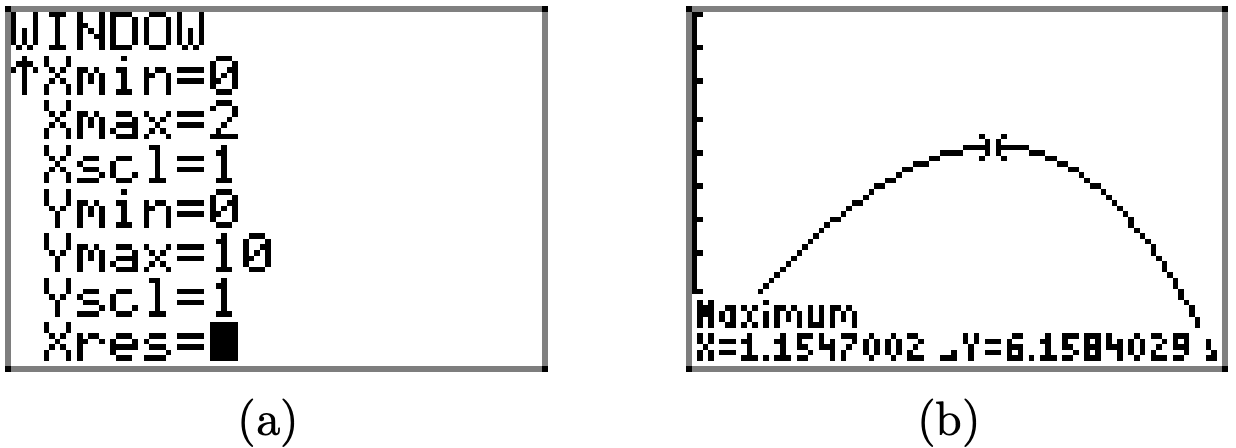
El resultado en la Figura$\PageIndex{13}$ (b) muestra que logramos un rectángulo de área máxima$A \approx 6.1584029$ si así lo elegimos$x \approx 1.1547002$. Recuerde, sus respuestas pueden diferir ligeramente según los límites izquierdo y derecho que seleccione, su suposición, y también debido al error de redondeo inherente en todas las calculadoras.

Ejercicio

En los Ejercicios 1 - 8, realizar cada una de las siguientes tareas para el polinomio dado.

Sin la ayuda de una calculadora, utilizar una técnica algebraica para identificar los ceros del polinomio dado. Facturar si es necesario.
En papel cuadriculado, configurar un sistema de coordenadas. Etiquete cada eje, pero escale solo el eje x. Usa los ceros y el comportamiento final para dibujar un “gráfico aproximado” del polinomio dado con la ayuda de una calculadora.
Clasificar cada extremo local como mínimo relativo o máximo relativo.Nota: No es necesario encontrar las coordenadas de los extremos relativos. En efecto, esto sería difícil con- fuera una calculadora. Todo lo que se requiere es que etiquetes cada extremo como un máximo o mínimo relativo

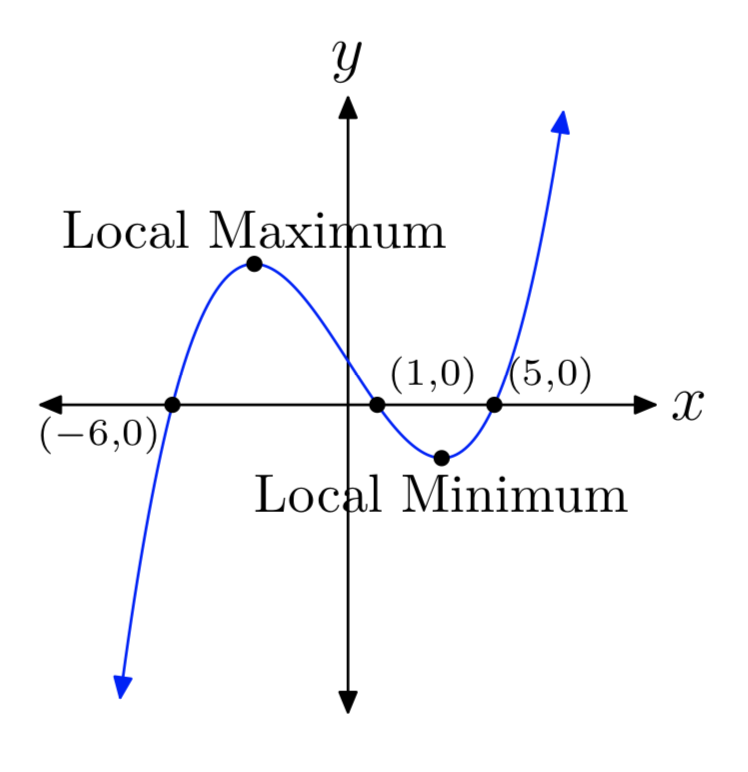
Ejercicio$\PageIndex{1}$

p (x) = (x+6) (x−1) (x−5)

Contestar: $Screen Shot 2019-09-02 at 9.01.27 AM.png$

Ejercicio$\PageIndex{2}$

p (x) = (x+2) (x−4) (x−7)

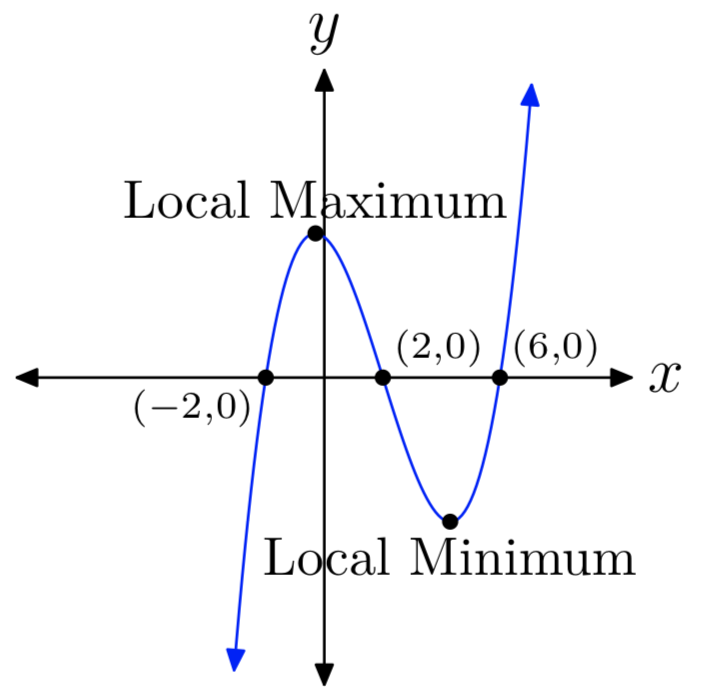
Ejercicio$\PageIndex{3}$

$p(x) = x^3−6x^2−4x+24$

Contestar: $Screen Shot 2019-09-02 at 9.02.10 AM.png$

Ejercicio$\PageIndex{4}$

$p(x) = x^3+x^2−36x−36$

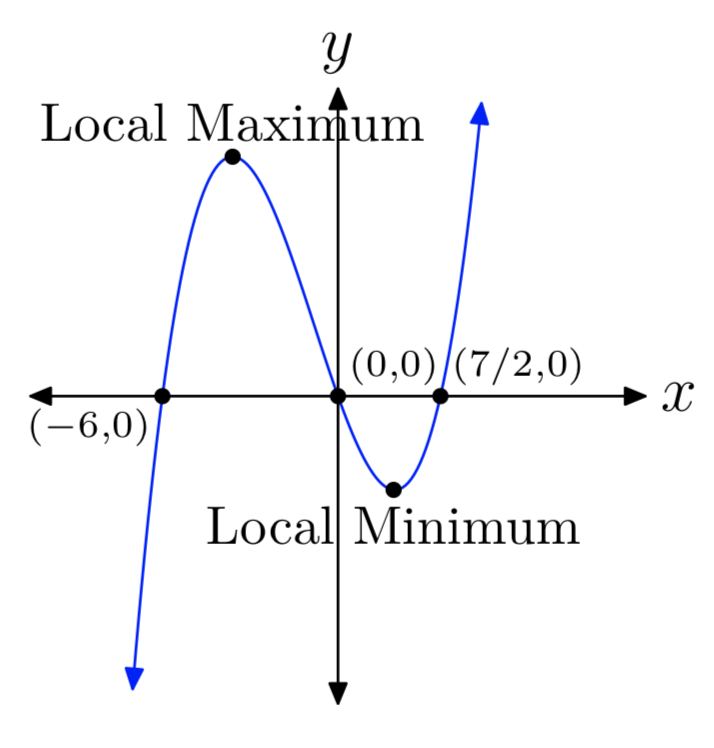
Ejercicio$\PageIndex{5}$

$p(x) = 2x^3+5x^2−42x$

Contestar: $Screen Shot 2019-09-02 at 9.02.45 AM.png$

Ejercicio$\PageIndex{6}$

$p(x) = 2x^3−3x^2−44x$

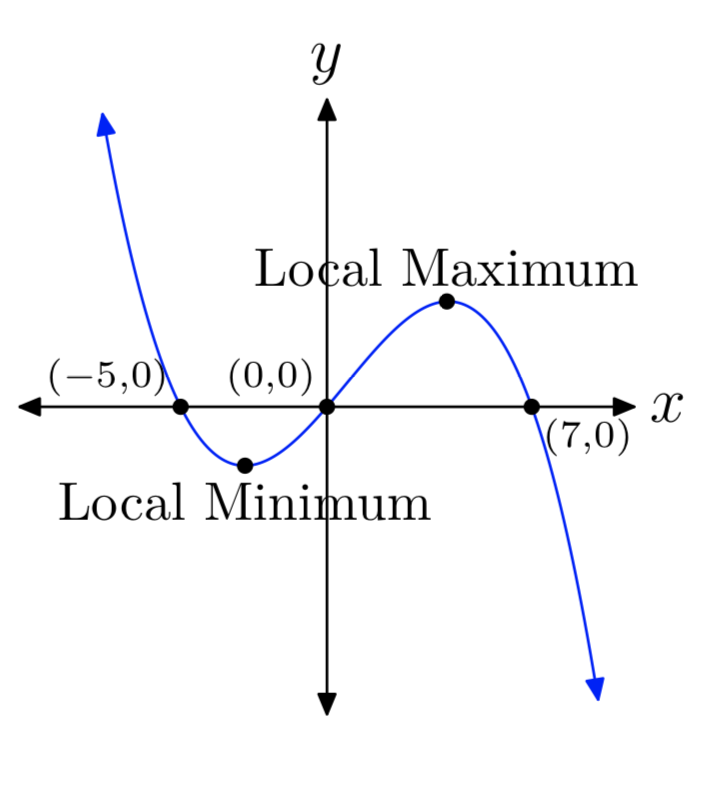
Ejercicio$\PageIndex{7}$

$p(x) = −2x^3+4x^2+70x$

Contestar: $Screen Shot 2019-09-02 at 9.03.27 AM.png$

Ejercicio$\PageIndex{8}$

$p(x) = −6x^3−21x^2+90x$

En los Ejercicios 9 - 16, realizar cada una de las siguientes tareas para el polinomio dado.

Utilice una calculadora gráfica para dibujar la gráfica del polinomio. Ajusta la ventana de visualización para que los extremos o “puntos de inflexión” del polinomio sean visibles en la ventana de visualización. Copia la imagen resultante en tu casa- papel de trabajo. Etiquete y escale cada eje con xmin, xmax, ymin e ymax.
Utiliza la utilidad máxima y/ o mínima en el menú CALC de tu calculadora para encontrar las coordenadas de los extremos. Etiquete cada extremo en su copia de tarea con sus coordenadas y indique si el extremo es un máximo relativo o absoluto o mini- mamá.

Ejercicio$\PageIndex{9}$

$p(x) = x^3−8x^2−5x+84$

Contestar

Max relativo: (−0.2960664, 84.753138)

Mín relativo: (5.6293978, −19.27166)

Las respuestas pueden diferir ligeramente debido a un error de redondación.

$Screen Shot 2019-09-02 at 9.05.38 AM.png$

Ejercicio$\PageIndex{10}$

$p(x) = x^3+3x^2−33x−35$

Ejercicio$\PageIndex{11}$

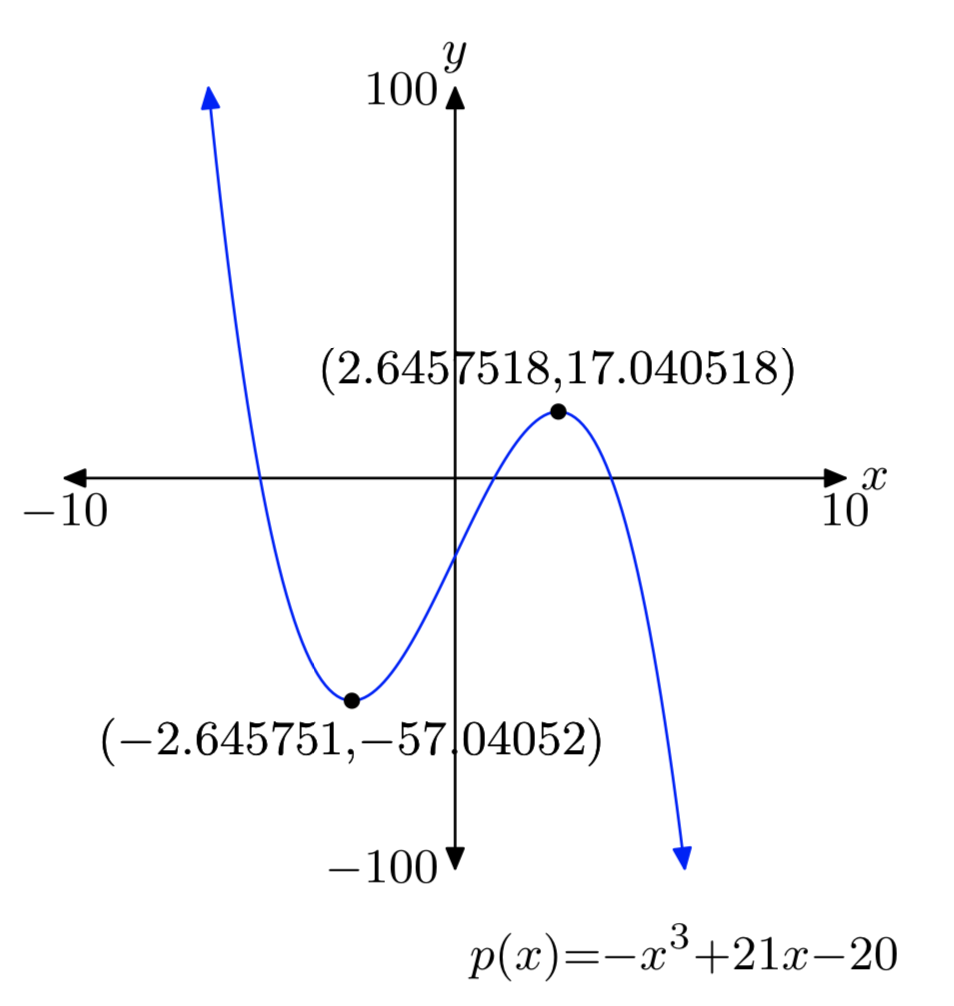
$p(x) = −x^3+21x−20$

Contestar

Mín relativo: (− 2. 645751, − 57. 04052)

Max relativo: (2. 6457518, 17. 040518)

Las respuestas pueden diferir ligeramente debido a un error de redondación.

$Screen Shot 2019-09-02 at 9.06.51 AM.png$

Ejercicio$\PageIndex{12}$

$p(x) = −x^3+5x^2+12x−36$

Ejercicio$\PageIndex{13}$

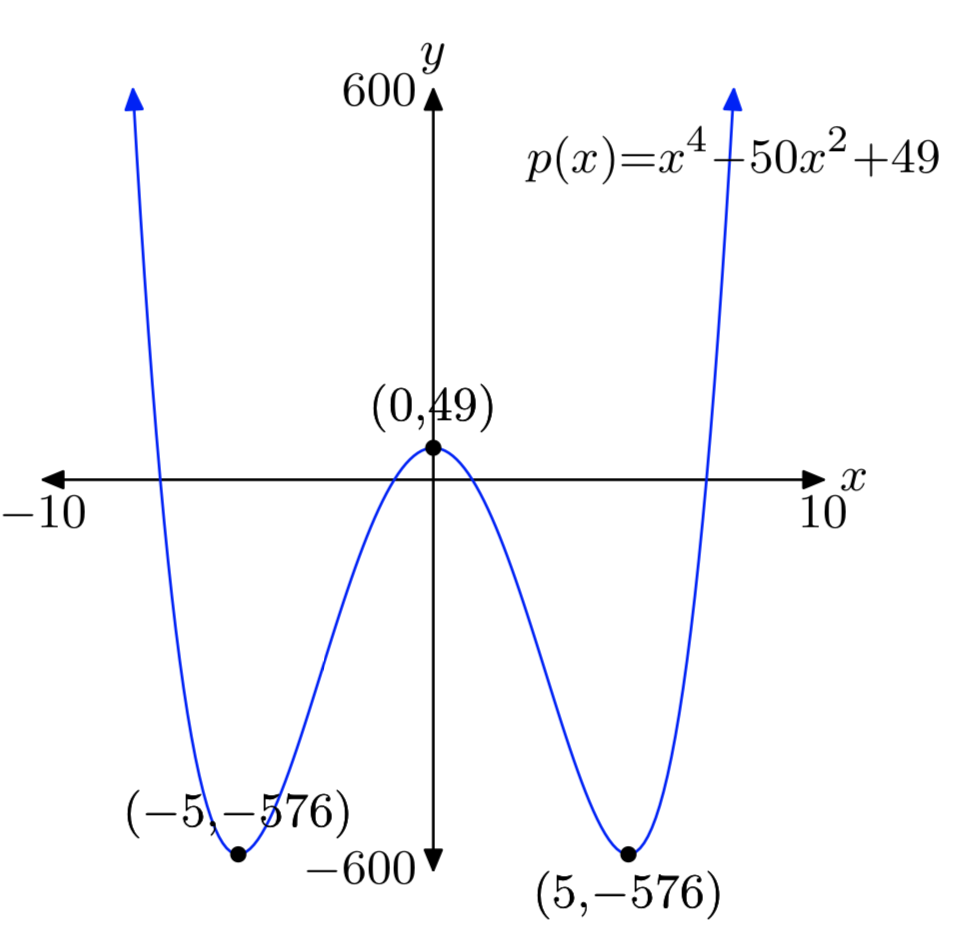
$p(x) = x^4−50x^2+49$

Contestar

Mín absoluto: (−5, −576)

Relativo máx: (0, 49)

Mín absoluto: (5, −576)

Las respuestas pueden diferir ligeramente debido a un error de redondación.

$Screen Shot 2019-09-02 at 9.08.17 AM.png$

Ejercicio$\PageIndex{14}$

$p(x) = x^4−29x^2+100$

Ejercicio$\PageIndex{15}$

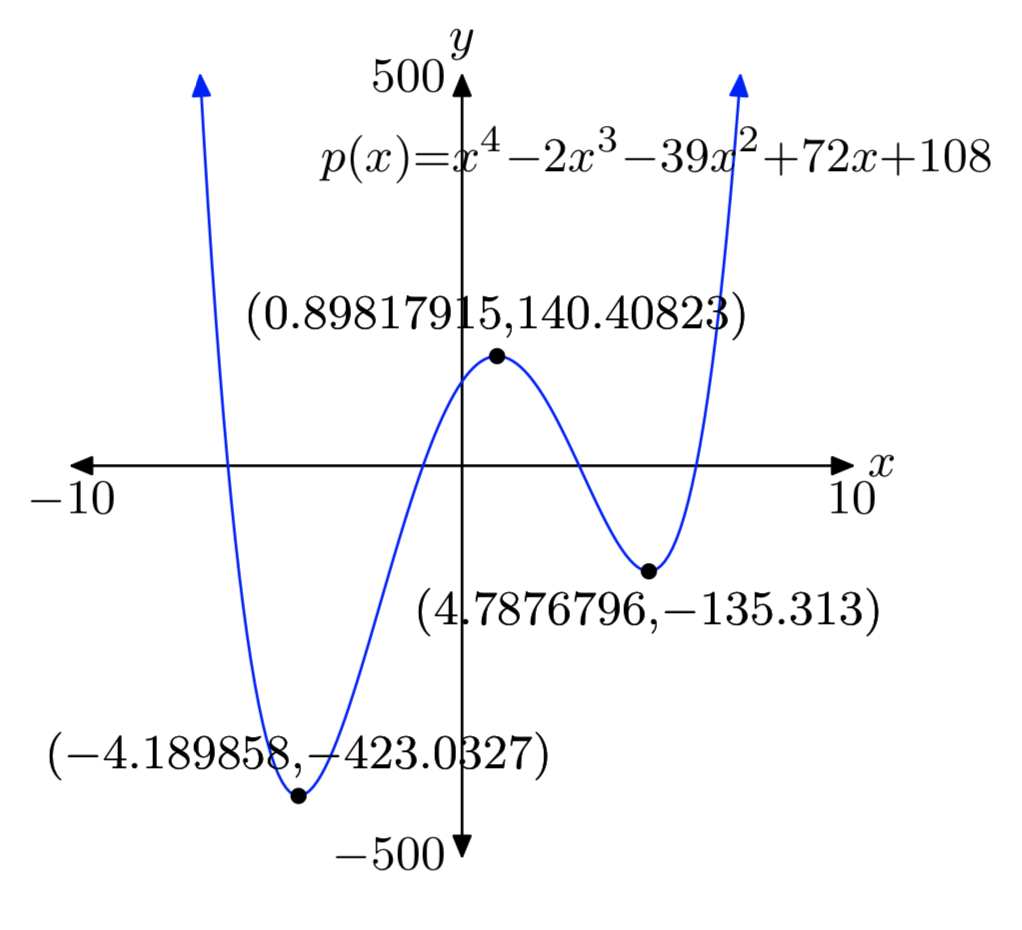
$p(x) = x^4−2x^3−39x^2+72x+108$

Contestar

Mín absoluto: (−4.189858, −423.0327)

Max relativo: (0.89817915, 140.40823)

Mín relativo: (4.7876796, −135.313)

Las respuestas pueden diferir ligeramente debido a un error de redondación.

$Screen Shot 2019-09-02 at 9.09.20 AM.png$

Ejercicio$\PageIndex{16}$

$p(x) = x^4−3x^3−31x^2+63x+90$

Ejercicio$\PageIndex{17}$

Una pieza cuadrada de cartón mide 12 pulgadas por lado. Cherie corta cuatro cuadrados más pequeños de cada esquina del cuadrado de cartón, arrojando el material a un lado. Luego dobla los lados del cartón restante para formar una caja abierta sin tapa. Encuentra las dimensiones de los cuadrados cortados de cada esquina de la pieza de cartón original para que Cherie maximice el volumen de la caja resultante. Realice cada uno de los siguientes pasos en su análisis.

Establecer una ecuación que determine el volumen de la caja en función de x, la longitud del borde de cada corte cuadrado desde las cuatro esquinas del cartón. Incluya las imágenes utilizadas para determinar esta función de volumen.
Indicar el dominio empírico de la función creada en la parte (a). Usa tu calculadora para bosquejar la gráfica de la función sobre este dominio empírico. Ajuste la ventana de visualización para que todos los extremos sean visibles en la ventana de visualización.
Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Utilice la utilidad máxima para encontrar las coordenadas del máximo absoluto en el dominio empírico de la función.
¿Cuáles son las medidas de los cuatro cuadrados cortados de cada esquina del cartón original? ¿Cuál es el volumen máximo de la caja?

Contestar

$V = x(12−2x)^2$
[0, 6]
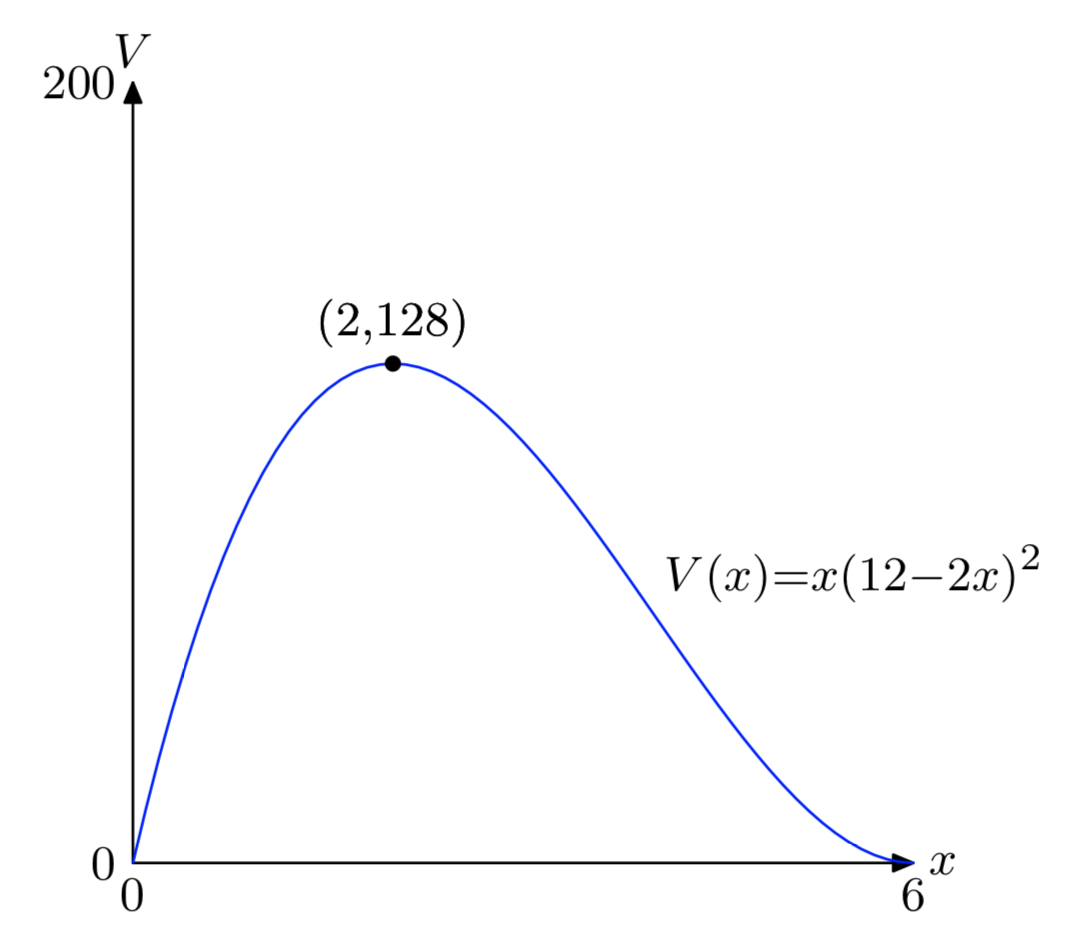
Máximo absoluto: (2, 128) $Screen Shot 2019-09-02 at 9.11.48 AM.png$
Corte el cuadrado de 2 pulgadas en un lado para producir una caja que tenga valor 128$in^3$.

Ejercicio$\PageIndex{18}$

Una pieza rectangular de cartón mide 8 pulgadas por 12 pulgadas. Schuyler corta cuatro cuadrados más pequeños de cada esquina del cuadrado de cartón, arrojando el material a un lado. Luego dobla los lados del cartón restante para formar una caja abierta sin tapa. Encuentra las dimensiones de los cuadrados cortados de cada esquina de la pieza de cartón original para que Schuyler maximice el volumen de la caja resultante. Realice cada uno de los siguientes pasos en su análisis.

Establecer una ecuación que determine el volumen de la caja en función de x, la longitud del borde de cada corte cuadrado desde las cuatro esquinas del cartón. Incluya las imágenes utilizadas para determinar esta función de volumen.
Indicar el dominio empírico de la función creada en la parte (a). Usa tu calculadora para bosquejar la gráfica de la función sobre este dominio empírico. Ajuste la ventana de visualización para que todos los extremos sean visibles en la ventana de visualización.
Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Utilice la utilidad máxima para encontrar las coordenadas del máximo absoluto en el dominio empírico de la función.
¿Cuáles son las medidas de los cuatro cuadrados cortados de cada esquina del cartón original? ¿Cuál es el volumen máximo de la caja?

Ejercicio$\PageIndex{19}$

Restringir la gráfica de la parábola$y = 4−\frac{x^2}{4}$ al primer cuadrante, luego inscribir un rectángulo dentro de la parábola, como se muestra en la figura que sigue.

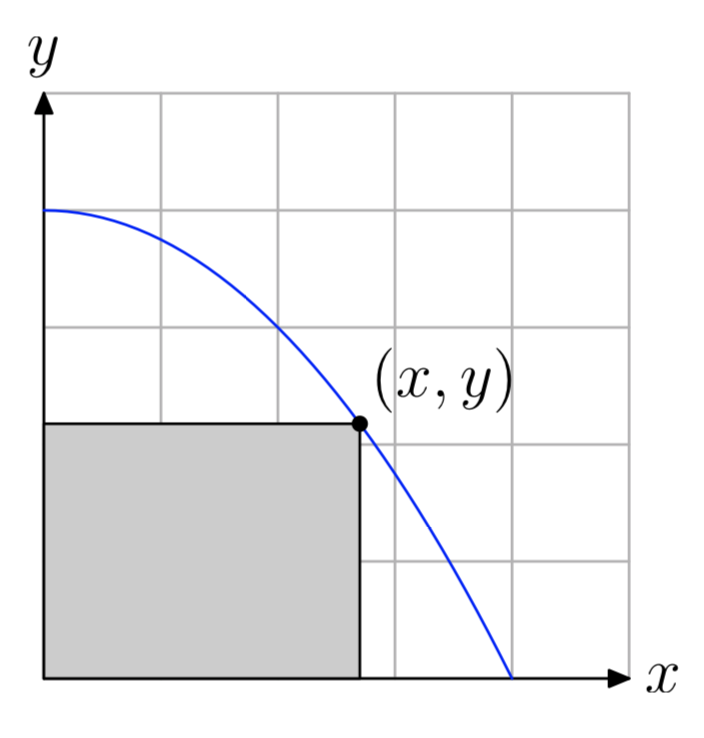
$Screen Shot 2019-09-02 at 8.55.44 AM.png$

Expresar el área del rectángulo inscrito en función de x.
Indicar el dominio empírico de la función definida en la parte (1). Utilice su calculadora para graficar la función de área sobre su dominio empírico. Ajuste los parámetros de la ventana para que todos los extremos sean visibles en la ventana de visualización.
Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Utilice la utilidad máxima para encontrar las coordenadas del máximo absoluto en el dominio empírico de la función. Etiquete su gráfica con este resultado.
¿Cuáles son las dimensiones del rectángulo de área máxima?

Contestar

$A = x(4−\frac{x^2}{4})$
[0, 4]
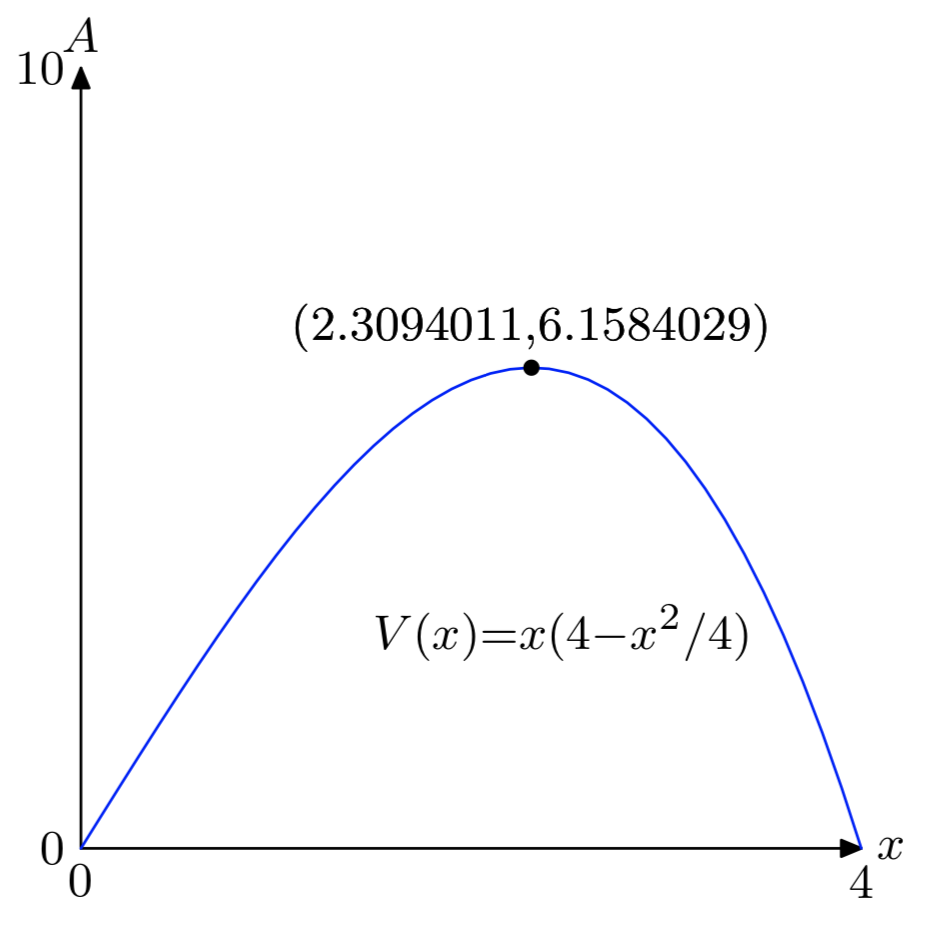
Máximo absoluto: (2.3094011, 6.1584029) $Screen Shot 2019-09-02 at 9.13.14 AM.png$
x = 2. 3094011, y = 2. 6666666

Ejercicio$\PageIndex{20}$

Restringir la gráfica de la parábola$y = 4−\frac{x^2}{4}$ al primer cuadrante, luego inscribir un triángulo dentro de la parábola, como se muestra en la figura que sigue.

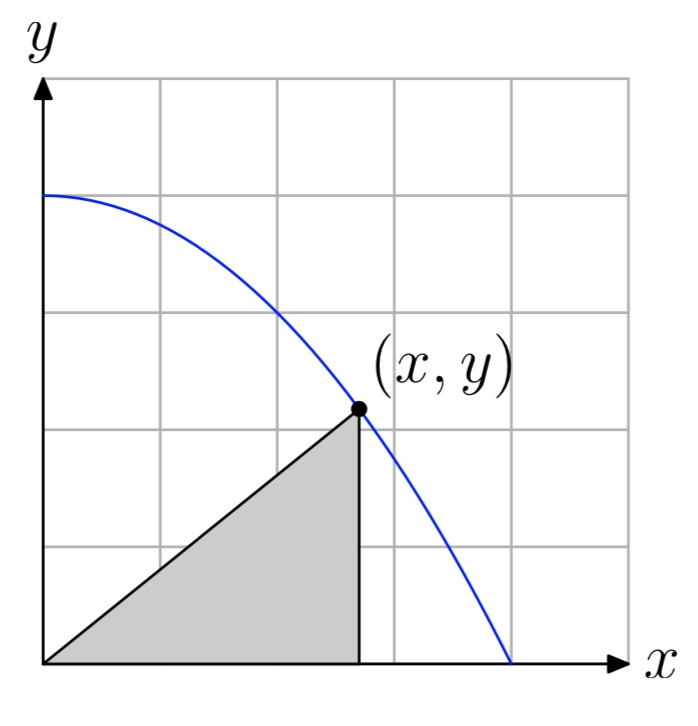
$Screen Shot 2019-09-02 at 8.59.33 AM.png$

Expresar el área del tri- ángulo inscrito en función de x.
Indicar el dominio empírico de la función definida en la parte (a). Utilice su calculadora para graficar la función de área sobre su dominio empírico. Ajuste los parámetros de la ventana para que todos los extremos sean visibles en la ventana de visualización.
Copia la imagen en tu ventana de visualización en tu papel de tarea. Etiquete y escale cada eje con xmin, xmax, ymin e ymax. Utilice la utilidad máxima para encontrar las coordenadas del máximo absoluto en el dominio empírico de la función. Etiquete su gráfica con este resultado.
¿Cuáles son la longitud de la base y la altura del triángulo de área máxima?

Search

Text Color

Text Size

Margin Size

Font Type