4.5: Teorema de Stokes

Hasta ahora los únicos tipos de integrales de línea que hemos discutido son aquellos a lo largo de las curvas en\(\mathbb{R}^ 2\). Pero las definiciones y propiedades que se cubrieron en las Secciones 4.1 y 4.2 se pueden extender fácilmente para incluir funciones de tres variables, de manera que ahora podemos discutir integrales de línea a lo largo de curvas en\(\mathbb{R}^ 3\).

Definición\(\PageIndex{1}\): Line Integrals

Para una función de valor real\(f (x, y, z)\) y una curva\(C\) en\(\mathbb{R}^ 3\), parametrizada por\(x = x(t), y = y(t), z = z(t), a ≤ t ≤ b\), la integral de línea\(f (x, y, z) \textbf{ along }C\) con respecto a la longitud del arco\(s\) es

\[\int_C f (x, y, z)\,ds = \int_a^b f (x(t), y(t), z(t))\sqrt{x ′ (t)^2 + y ′ (t)^2 + z ′ (t)^2}\,dt.\label{Eq4.34}\]

La línea integral de\(f (x, y, z)\) lo largo\(C\) con respecto a\(x\) es

\[\int_C f (x, y, z)\,dx =\int_a^b f (x(t), y(t), z(t)) x ′ (t)\,dt.\label{Eq4.35}\]

La línea integral de\(f (x, y, z)\) lo largo\(C\) con respecto a\(y\) es

\[\int_C f (x, y, z)\,d y =\int_a^b f (x(t), y(t), z(t)) y ′ (t)\,dt .\label{Eq4.36}\]

La línea integral de\(f (x, y, z)\) lo largo\(C\) con respecto a\(z\) es

\[\int_C f (x, y, z)\,dz =\int_a^b f (x(t), y(t), z(t)) z ′ (t)\,dt .\label{Eq4.37}\]

Similar al caso de dos variables, si\(f (x, y, z) ≥ 0\) entonces la integral de línea\(\int_C f (x, y, z)\,ds\) puede pensarse como el área total de la “cerca de piquete” de altura\(f (x, y, z)\) en cada punto a lo largo de la curva\(C\) en\(\mathbb{R}^ 3\).

Los campos vectoriales en se\(\mathbb{R}^ 3\) definen de manera similar a los de\(\mathbb{R}^ 2\), lo que nos permite definir la integral de línea de un campo vectorial a lo largo de una curva en\(\mathbb{R}^ 3\).

Definición\(\PageIndex{2}\)

Para un campo vectorial\(\textbf{f}(x, y, z) = P(x, y, z)\textbf{i}+Q(x, y, z)\textbf{j}+R(x, y, z)\textbf{k}\) y una curva\(C\)\(\mathbb{R}^ 3\) con una parametrización suave\(x = x(t), y = y(t), z = z(t), a ≤ t ≤ b\), la integral de línea\(f\) a lo largo\(C\) es

\[\begin{align} \int_C \textbf{f} \cdot d\textbf{r} &=\int_C P(x, y, z)\,dx +\int_C Q(x, y, z)\,d y + \int_C R(x, y, z)\,dz \label{Eq4.38} \\[4pt] &=\int_a^b \textbf{f}(x(t), y(t), z(t))\cdot \textbf{r} ′ (t)dt ,\label{Eq4.39} \\[4pt] \end{align}\]

donde\(\textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}+ z(t)\textbf{k}\) está el vector de posición para los puntos en\(C\).

Similar al caso de dos variables, si\(\textbf{f}(x, y, z)\) representa la fuerza aplicada a un objeto en un punto,\((x, y, z)\) entonces la integral de línea\(\int_C \textbf{f}\cdot d\textbf{r}\) representa el trabajo realizado por esa fuerza al mover el objeto a lo largo de la curva\(C\) en\(\mathbb{R}^ 3\).

Algunos de los resultados más importantes que necesitaremos para las integrales de línea\(\mathbb{R}^ 3\) se indican a continuación sin pruebas (las pruebas son similares a sus equivalentes de dos variables).

Teorema\(\PageIndex{1}\)

Para un campo vectorial\(\textbf{f}(x, y, z) = P(x, y, z)\textbf{i} +Q(x, y, z)\textbf{j} + R(x, y, z)\textbf{k}\) y una curva\(C\) con un vector de parametrización\(x = x(t), y = y(t), z = z(t), a ≤ t ≤ b\) y posición suaves\(\textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}+ z(t)\textbf{k}\),

\[\int_C \textbf{f}\cdot d\textbf{r} = \int_C \textbf{f}\cdot \textbf{T}\,ds,\label{Eq4.40}\]

donde\(\textbf{T}(t) = \dfrac{\textbf{r} ′ (t)}{ \lVert \textbf{r} ′ (t) \rVert }\) es el vector tangente unitario a\(C\) at\((x(t), y(t), z(t))\).

Teorema\(\PageIndex{2}\): Chain Rule

Si\(w = f (x, y, z)\) es una función continuamente diferenciable de\(x, y, \text{ and }z, \text{ and }x = x(t), y = y(t) \text{ and }z = z(t)\) son funciones diferenciables de\(t, \text{ then }w\) es una función diferenciable de\(t\), y

\[\dfrac{dw}{ dt} = \dfrac{∂w}{ ∂x}\dfrac{ dx}{ dt} + \dfrac{∂w}{ ∂y}\dfrac{ d y}{ dt} + \dfrac{∂w }{∂z}\dfrac{ dz}{ dt}.\label{Eq4.41}\]

Además, si\(x = x(t_1 ,t_2), y = y(t_1 ,t_2) \text{ and }z = z(t_1 ,t_2)\) son función continuamente diferenciable de\((t_1 ,t_2)\), entonces

\[\dfrac{∂w}{ ∂t_1} = \dfrac{∂w}{ ∂x}\dfrac{ ∂x}{ ∂t_1} + \dfrac{∂w}{ ∂y}\dfrac{ ∂y}{ ∂t_1} +\dfrac{∂w}{ ∂z}\dfrac{ ∂z}{ ∂t_1} \label{Eq4.42}\]

y

\[\dfrac{∂w}{ ∂t_2} = \dfrac{∂w}{ ∂x}\dfrac{ ∂x}{ ∂t_2} + \dfrac{∂w}{ ∂y}\dfrac{ ∂y}{ ∂t_2} +\dfrac{∂w}{ ∂z}\dfrac{ ∂z}{ ∂t_2} \label{Eq4.43}\]

Teorema\(\PageIndex{3}\): Potential

Dejar\(\textbf{f}(x, y, z) = P(x, y, z)\textbf{i} + Q(x, y, z)\textbf{j} + R(x, y, z)\textbf{k}\) ser un campo vectorial en algún sólido\(S\), con funciones\(P, Q \text{ and }R\) continuamente diferenciables encendidas\(S\). Dejar\(C\) ser una curva suave en\(S\) parametrizado por\(x = x(t), y = y(t), z = z(t), a ≤ t ≤ b\). Supongamos que hay una función de valor real\(F(x, y, z)\) tal que\(∇F = \textbf{f} \text{ on }S\). Entonces

\[\int_C \textbf{f}\cdot d\textbf{r} = F(B) − F(A) ,\label{Eq4.44}\]

donde\(A = (x(a), y(a), z(a)) \text{ and }B = (x(b), y(b), z(b))\) están los puntos finales de\(C\).

Corolario

Si un campo vectorial \(\ textbf {f}\) tiene un potencial en un sólido\(S\), entonces\(\oint_C \textbf{f}\cdot d\textbf{r} = 0\) para cualquier curva cerrada\(C\) en\(S\) (es decir,\(\oint_C ∇F\cdot d\textbf{r} = 0\) para cualquier función de valor real\(F(x, y, z))\).

Ejemplo\(\PageIndex{1}\)

Dejar\(f (x, y, z) = z\) y dejar\(C\) ser la curva en\(\mathbb{R}^ 3\) parametrizada por

\[\nonumber x = t\sin t ,\quad y = t \cos t ,\quad z = t ,\quad 0 ≤ t ≤ 8π .\]

Evaluar\(\int_C f (x, y, z)\,ds\). (Nota:\(C\) se llama hélice cónica. Ver Figura 4.5.1).

Solución

Desde entonces\(x ′ (t) = \sin t+ t \cos t, y ′ (t) = \cos t− t\sin t, \text{ and }z ′ (t) = 1\), tenemos

\[\nonumber \begin{align}x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2 &= (\sin^2 t+2t\sin t \cos t+ t^ 2 \cos^2 t)+(\cos^2 t−2t\sin t \cos t+ t^ 2 \sin^2 t)+1 \\[4pt] \nonumber &=t^ 2 (\sin^2 t+\cos^2 t)+\sin^2 t+\cos^2 t+1 \\[4pt] \nonumber &=t^2 +2, \\[4pt] \end{align}\]

así ya que\(f (x(t), y(t), z(t)) = z(t) = t\) a lo largo de la curva\(C\), entonces

\[\nonumber \begin{align} \int_C f (x, y, z)\,ds &= \int_0^{8\pi} f (x(t), y(t), z(t))\sqrt{x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2}\,dt \\[4pt] \nonumber &=\int_0^{8\pi} t\sqrt{t^2+2}\,dt \\[4pt] \nonumber &= \left ( \dfrac{1}{3} (t^ 2 +2)^{3/2} \right ) \Big |_0^{8\pi} = \dfrac{1}{3} \left ( (64π^ 2 +2)^{3/2} −2 \sqrt{ 2} \right ). \\[4pt] \end{align}\]

Figura 4.5.1 Hélice cónica\(C\)

Ejemplo\(\PageIndex{2}\)

Let\(\textbf{f}(x, y, z) = x\textbf{i} + y\textbf{j}+ 2z\textbf{k}\) Ser un campo vectorial en\(\mathbb{R}^ 3\). Usando la misma curva\(C\) del Ejemplo 4.12, evalúe\(\int_C \textbf{f}\cdot d\textbf{r}\).

Solución:

Es fácil ver que\(F(x, y, z) = \dfrac{x^ 2}{ 2} + \dfrac{y^ 2}{ 2} + z^ 2\) es un potencial para\(\textbf{f}(x, y, z)\) (i.e\(∇F = \textbf{f})\).

Entonces por Teorema 4.12 sabemos que

\[\nonumber \begin{align} \int_C \textbf{f}\cdot d\textbf{r} &=F(B) − F(A) , \text{ where }A = (x(0), y(0), z(0)) \text{ and }B = (x(8π), y(8π), z(8π)),\text{ so} \\[4pt] \nonumber &=F(8π\sin 8π,8π\cos 8π,8π) − F(0\sin 0,0\cos 0,0) \\[4pt] \nonumber &=F(0,8π,8π) − F(0,0,0) \\[4pt] \nonumber &= 0+ \dfrac{(8π)^ 2}{ 2} +(8π)^ 2 −(0+0+0) = 96π^ 2 . \\[4pt] \end{align}\]

Ahora discutiremos una generalización del Teorema de Green en\(\mathbb{R}^ 2\) superficies orientables en\(\mathbb{R}^ 3\), llamado Teorema de Stokes. Una superficie\(Σ\) en\(\mathbb{R}^ 3\) es orientable si hay un campo vectorial continuo N de\(\mathbb{R}^ 3\) tal manera que N es distinto de cero y normal a\(Σ\) (es decir, perpendicular al plano tangente) en cada punto de\(Σ\). Decimos que tal N es un campo vectorial normal.

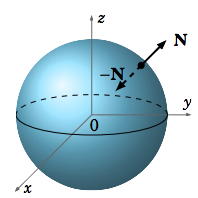
Por ejemplo, la esfera unitaria\(x^ 2+y^ 2+z^ 2 = 1\) es orientable, ya que el campo vectorial continuo\(\textbf{N}(x, y, z) = x\textbf{i}+ y\textbf{j}+z\textbf{k}\) es distinto de cero y es normal a la esfera en cada punto. De hecho,\(−\textbf{N}(x, y, z)\) es otro campo vector normal (ver Figura 4.5.2). Vemos en este caso que\(\textbf{N}(x, y, z)\) es lo que hemos llamado un vector normal exterior, y\(−\textbf{N}(x, y, z)\) es un vector normal hacia adentro. Estos campos vectoriales normales “externos” e “internos” en la esfera corresponden a un lado “externo” e “interno”, respectivamente, de la esfera. Es decir, decimos que la esfera es una superficie de dos lados. Más o menos, “de dos lados” significa “orientable”. Otros ejemplos de superficies de dos lados, y por lo tanto orientables, son cilindros, paraboloides, elipsoides y planos.

Figura 4.5.2

Quizás se esté preguntando qué tipo de superficie no tendría dos lados. Un ejemplo es la tira de Möbius, que se construye tomando un rectángulo delgado y conectando sus extremos en las esquinas opuestas, dando como resultado una tira “retorcida” (ver Figura 4.5.3).

Figura 4.5.3: Tira de Möbius

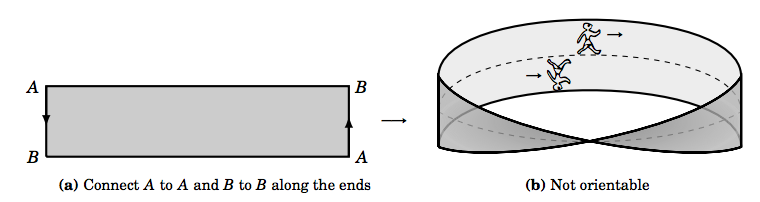
Si te imaginas caminar por una línea por el centro de la franja de Möbius, como en la Figura 4.5.3 (b), entonces llegas de vuelta al mismo lugar desde el que partiste pero ¡al revés! Es decir, tu orientación cambió a pesar de que tu movimiento era continuo a lo largo de esa línea central. De manera informal, pensando en tu dirección vertical como un campo vectorial normal a lo largo de la franja, hay una discontinuidad en tu punto de partida (y, de hecho, en cada punto) ya que tu dirección vertical toma allí dos valores diferentes. La tira de Möbius tiene solo un lado, y por lo tanto es no orientable.

Para una superficie orientable\(Σ\) que tenga una curva límite\(C\), elija un vector normal unitario n de tal manera que si caminó junto\(C\) con la cabeza apuntando en la dirección de n, entonces la superficie estaría a su izquierda. Decimos en esta situación que n es un vector normal unitario positivo y que\(C\) se recorre n - positivamente. Ahora podemos exponer el Teorema de Stokes:

Teorema\(\PageIndex{4}\): Stoke's Theorem

Dejar\(Σ\) ser una superficie orientable en\(\mathbb{R}^ 3\) cuyo límite es una simple curva cerrada\(C\), y dejar\(\textbf{f}(x, y, z) = P(x, y, z)\textbf{i} +Q(x, y, z)\textbf{j} + R(x, y, z)\textbf{k}\) ser un campo vectorial suave definido en algún subconjunto de los\(\mathbb{R}^ 3\) que contiene\(Σ\). Entonces

\[\oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_Σ (\text{curl }\textbf{f})\cdot \textbf{n}\,dσ , \label{Eq4.45}\]

donde

\[\text{curl }\textbf{f} = \left ( \dfrac{∂R}{ ∂y}-\dfrac{∂Q}{ ∂z} \right ) \textbf{i} + \left ( \dfrac{∂P}{ ∂z} - \dfrac{∂R}{ ∂x} \right ) \textbf{j} + \left ( \dfrac{∂Q}{ ∂x} -\dfrac{∂P}{ ∂y} \right ) \textbf{k},\label{Eq4.46}\]

n es un vector normal unitario positivo sobre\(Σ\), y\(C\) es atravesado n - positivamente.

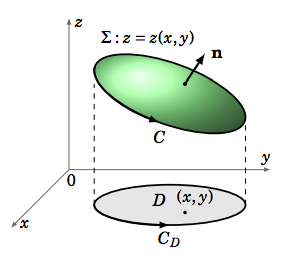
Prueba: Como el caso general está más allá del alcance de este texto, probaremos el teorema solo para el caso especial donde\(Σ\) está la gráfica de\(z = z(x, y)\) para alguna función fluida de valor real que\(z(x, y), \text{ with }(x, y)\) varía sobre una región\(D\) en\(\mathbb{R}^ 2\).

Proyectando\(Σ\) sobre el\(x y\) plano, vemos que la curva cerrada\(C\) (la curva límite de\(Σ\)) se proyecta sobre una curva cerrada\(C_D\) que es la curva límite de\(D\) (ver Figura 4.5.4). Suponiendo que\(C\) tiene una parametrización suave, su proyección\(C_D\) en el\(x y\) plano también tiene una parametrización suave, digamos

Figura 4.5.4

\[\nonumber C_D\, :\, x = x(t) , y = y(t) , a ≤ t ≤ b ,\]

y así se\(C\) puede parametrizar (in\(\mathbb{R}^ 3\)) como

\[\nonumber C \,:\, x = x(t) ,\, y = y(t) ,\, z = z(x(t), y(t)) ,\, a ≤ t ≤ b ,\]

ya que la curva\(C\) es parte de la superficie\(z = z(x, y)\). Ahora bien, por la Regla de la Cadena (Teorema 4.4 en la Sección 4.2)\(z = z(x(t), y(t)) \text{ as a function of }t\), pues, sabemos que

\[\nonumber z ′ (t) = \dfrac{∂z}{ ∂x} x ′ (t) + \dfrac{∂z}{ ∂y} y ′ (t) ,\]

y así

\[\nonumber \begin{align} \oint_C \textbf{f}\cdot d\textbf{r} &= \int_C P(x, y, z)\,dx+Q(x, y, z)\,d y+ R(x, y, z)\,dz \\[4pt] \nonumber &=\int_a^b \left ( P x′ (t)+Q y′ (t)+ R \left ( \dfrac{∂z}{ ∂x} x ′ (t)+ \dfrac{∂z}{ ∂y} y ′ (t) \right ) \right ) \,dt \\[4pt] \nonumber &=\int_a^b \left ( \left ( P + R \dfrac{∂z}{ ∂x} \right ) x ′ (t)+ \left ( Q + R \dfrac{∂z}{ ∂y} \right ) y ′ (t) \right ) \,dt \\[4pt] \nonumber &=\int_{C_D} \tilde P (x, y)\,dx+\tilde Q (x, y)\,d y , \\[4pt] \end{align}\]

donde

\[\nonumber \begin{align} &\tilde P (x, y) = P(x, y, z(x, y)) + R(x, y, z(x, y)) \dfrac{∂z}{ ∂x} (x, y) ,\text{ and} \\[4pt] \nonumber &\tilde Q (x, y) = Q(x, y, z(x, y)) + R(x, y, z(x, y)) \dfrac{∂z}{ ∂y} (x, y) \\[4pt] \end{align}\]

para\((x, y) \text{ in }D\). Así, por el Teorema de Green aplicado a la región\(D\), tenemos

\[\oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_D \left ( \dfrac{∂\tilde Q}{ ∂x} − \dfrac{∂\tilde P}{ ∂y}\right ) \,dA.\label{Eq4.47}\]

Por lo tanto,

\[\nonumber \begin{align} \dfrac{∂\tilde Q}{ ∂x} &= \dfrac{∂}{ ∂x} \left ( Q(x, y, z(x, y))+ R(x, y, z(x, y)) \dfrac{∂z}{ ∂y} (x, y) \right ),\text{ so by the Product Rule we get} \\[4pt] \nonumber &= \dfrac{∂}{ ∂x} (Q(x, y, z(x, y)))+\left (\dfrac{∂}{ ∂x} R(x, y, z(x, y)) \right ) \dfrac{∂z}{ ∂y} (x, y)+R(x, y, z(x, y)) \dfrac{∂}{ ∂x} \left ( \dfrac{∂z}{ ∂y} (x, y) \right ) \\[4pt] \end{align}\]

Ahora, por la Ecuación\ ref {Eq4.42} en el Teorema 4.11, tenemos

\[\nonumber \begin{align} \dfrac{∂}{ ∂x} (Q(x, y, z(x, y)))&= \dfrac{∂Q}{ ∂x}\dfrac{ ∂x}{ ∂x}+\dfrac{∂Q}{ ∂y}\dfrac{ ∂y}{ ∂x}+\dfrac{∂Q}{ ∂z}\dfrac{ ∂z}{ ∂x} \\[4pt] \nonumber &= \dfrac{∂Q}{ ∂x} \cdot 1 + \dfrac{∂Q}{ ∂y} \cdot 0 + \dfrac{∂Q}{ ∂z}\dfrac{ ∂z}{ ∂x} \\[4pt] \nonumber &= \dfrac{∂Q}{ ∂x} + \dfrac{∂Q}{∂z}\dfrac{ ∂z}{ ∂x} . \\[4pt] \end{align}\]

Del mismo modo,

\[\nonumber \dfrac{∂}{ ∂x} (R(x, y, z(x, y))) = \dfrac{∂R}{ ∂x} + \dfrac{∂R}{ ∂z}\dfrac{ ∂z}{ ∂x} .\]

Por lo tanto,

\[\nonumber \begin{align}\dfrac{∂\tilde Q}{ ∂x} &=\dfrac{∂Q}{ ∂x} + \dfrac{∂Q}{ ∂z}\dfrac{ ∂z}{ ∂x} + \left ( \dfrac{∂R}{ ∂x} + \dfrac{∂R}{ ∂z}\dfrac{ ∂z}{ ∂x} \right ) \dfrac{∂z }{∂y}+R(x, y, z(x, y)) \dfrac{∂^2 z}{ ∂x∂y} \\[4pt] \nonumber &=\dfrac{∂Q}{ ∂x} + \dfrac{∂Q}{ ∂z}\dfrac{ ∂z}{ ∂x} + \dfrac{∂R}{ ∂x}\dfrac{ ∂z}{ ∂y}+\dfrac{∂R}{ ∂z}\dfrac{ ∂z}{ ∂x}\dfrac{ ∂z}{ ∂y} + R \dfrac{∂^2 z}{ ∂x∂y} . \\[4pt] \end{align}\]

De manera similar, podemos calcular

\[\nonumber \dfrac{∂\tilde P}{ ∂y} = \dfrac{∂P}{ ∂y} + \dfrac{∂P}{ ∂z}\dfrac{ ∂z}{ ∂y} + \dfrac{∂R}{ ∂y}\dfrac{ ∂z}{ ∂x} + \dfrac{∂R}{ ∂z}\dfrac{ ∂z}{ ∂y}\dfrac{ ∂z}{ ∂x} +R\dfrac{∂^2 z}{ ∂y∂x} .\]

Así restando da

\[\dfrac{∂\tilde Q}{ ∂x} - \dfrac{∂\tilde P}{ ∂y} = \left ( \dfrac{∂Q}{ ∂z} − \dfrac{∂R}{ ∂y} \right ) \dfrac{∂z}{ ∂x} + \left ( \dfrac{∂R}{ ∂x} − \dfrac{∂P}{ ∂z} \right ) \dfrac{∂z}{ ∂y} + \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \label{Eq4.48}\]

ya que\(\dfrac{∂^2 z}{ ∂x∂y} = \dfrac{∂^2 z}{ ∂y∂x}\) por la suavidad de\(z = z(x, y)\). De ahí, por la Ecuación\ ref {Eq4.47},

\[\oint_C \textbf{f}\cdot d\textbf{r} = \iint_D \left ( - \left (\dfrac{∂R}{ ∂y} − \dfrac{∂Q}{ ∂z} \right ) \dfrac{∂z}{ ∂x} - \left ( \dfrac{∂P}{ ∂z} − \dfrac{∂R}{ ∂x} \right ) \dfrac{∂z}{ ∂y} + \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \right ) \,dA \label{Eq4.49}\]

después de factorizar un −1 de los términos en los dos primeros productos en la Ecuación\ ref {Eq4.48}.

Ahora, recordemos de la Sección 2.3 (ver p.76) que el vector\(\textbf{N} = − \dfrac{∂z}{ ∂x}\textbf{ i}− \dfrac{∂z}{ ∂y}\textbf{j}+\textbf{k}\) es normal al plano tangente a la superficie\(z = z(x, y)\) en cada punto de\(Σ\). Por lo tanto,

\[\nonumber \textbf{n} = \dfrac{\textbf{N}}{\lVert \textbf{N} \rVert } = \dfrac{− \dfrac{∂z}{ ∂x}\textbf{ i}− \dfrac{∂z}{ ∂y}\textbf{j}+\textbf{k}}{\sqrt{1+\left ( \dfrac{∂z}{ ∂x} \right ) ^2+\left ( \dfrac{∂z}{ ∂y} \right )^2}}\]

es de hecho una unidad positiva de vector normal a\(Σ\) (ver Figura 4.5.4). De ahí, usando la parametrización\(\textbf{r}(x, y) = x\textbf{i} + y\textbf{j} + z(x, y)\textbf{k},\text{ for }(x, y) \text{ in }D\), de la superficie\(Σ\), tenemos\(\dfrac{∂\textbf{r}}{ ∂x} = \textbf{i} + \dfrac{∂z}{ ∂x}\textbf{k}\) y\(\dfrac{∂\textbf{r}}{ ∂y} = \textbf{j}+ \dfrac{∂z}{ ∂y}\textbf{k}\), y así\(\lVert \dfrac{ ∂\textbf{r}}{ ∂x} \times \dfrac{∂\textbf{r}}{ ∂y} \rVert = \sqrt{ 1+ \left ( \dfrac{∂z}{ ∂x} \right )^2 + \left ( \dfrac{∂z}{ ∂y} \right )^2}\). Así vemos que usando la ecuación\ ref {Eq4.46} para curl f, tenemos

\[\nonumber \begin{align} \iint\limits_Σ (\text{curl }\textbf{f})\cdot \textbf{n} \,dσ &=\iint\limits_D (\text{curl }\textbf{f}) \Big \lVert \dfrac{∂\textbf{r}}{ ∂x}\times \dfrac{∂\textbf{r}}{ ∂y} \Big \rVert \, dA \\[4pt] \nonumber &=\iint\limits_D \left ( \left ( \dfrac{∂R}{ ∂y} − \dfrac{∂Q}{ ∂z} \right )\textbf{i} + \left ( \dfrac{∂P}{ ∂z} − \dfrac{∂R}{ ∂x} \right ) \textbf{j} + \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \textbf{k} \right ) \cdot \left ( -\dfrac{∂z}{ ∂x}\textbf{i}− \dfrac{∂z}{ ∂y}\textbf{j}+\textbf{k} \right ) \,dA \\[4pt] \nonumber &=\iint\limits_D \left ( - \left ( \dfrac{∂R}{ ∂y} − \dfrac{∂Q}{ ∂z} \right )\, \dfrac{∂z}{ ∂x} - \left ( \dfrac{∂P}{ ∂z} − \dfrac{∂R}{ ∂x} \right ) \, \dfrac{∂z}{ ∂y} + \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \right ) \, dA, \\[4pt] \end{align}\]

que, al comparar con la Ecuación\ ref {Eq4.49}, prueba el Teorema.

\(\tag{\(\textbf{QED}\)}\)

Nota: La condición en el Teorema de Stokes de que la superficie\(Σ\) tenga un vector normal unitario positivo n (continuamente variable) y una curva límite\(C\) atravesada n - positivamente se puede expresar con mayor precisión de la siguiente manera: si\(\textbf{r}(t)\) es el vector de posición para\(C\) y \(\textbf{T}(t) = \textbf{r} ′ (t)/ \rVert \textbf{r} ′ (t) \rVert\)es el vector tangente unitario a\(C\), luego los vectores T, n, T\(\times\) n forman un sistema diestro.

Además, cabe señalar que el Teorema de Stokes se mantiene incluso cuando la curva límite\(C\) es lisa por partes.

Ejemplo\(\PageIndex{3}\)

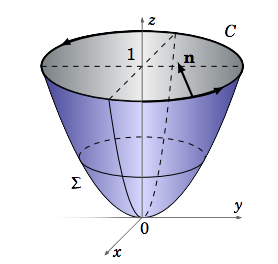
Verificar el Teorema de Stokes para\(\textbf{f}(x, y, z) = z \textbf{i} + x\textbf{j} + y\textbf{k}\) cuando\(Σ\) es el paraboloide\(z = x^ 2 + y^ 2\) tal que\(z ≤ 1\) (ver Figura 4.5.5).

Figura 4.5.5\(\, z = x^ 2 + y^ 2\)

Solución:

El vector normal de la unidad positiva a la superficie\(z = z(x, y) = x^ 2 + y^ 2\) es

\[\nonumber \textbf{n} = \dfrac{−\dfrac{∂z}{ ∂x}\textbf{i}− \dfrac{∂z}{ ∂y}\textbf{j}+\textbf{k}}{\sqrt{1+ \left ( \dfrac{∂z}{ ∂x} \right )^2+\left ( \dfrac{∂z}{ ∂y} \right )^2}}= \dfrac{−2x\textbf{i}−2y\textbf{j}+\textbf{k}}{\sqrt{1+4x^2 +4y^2}},\]

y rizo f = (1−0) i + (1−0) j + (1−0) k = i + j + k, entonces

\[\nonumber (\text{curl }\textbf{f})\cdot \textbf{n} = (−2x−2y+1)/\sqrt{1+4x^ 2 +4y^ 2} .\]

Dado que se\(Σ\) puede parametrizar como\(\textbf{r}(x, y) = x\textbf{i} + y\textbf{j} + (x^ 2 + y^ 2 )\textbf{k} \text{ for }(x, y) \text{ in the region }D = {(x, y) : x^ 2 + y^ 2 ≤ 1}\), entonces

\[\nonumber \begin{align} \iint\limits_Σ (\text{curl }\textbf{f})\cdot \textbf{n}\,dσ &=\iint\limits_D (\text{curl }\textbf{f}) \Big \lVert \dfrac{∂\textbf{r}}{ ∂x}\times \dfrac{∂\textbf{r}}{ ∂y} \Big \rVert \, dA \\[4pt] \nonumber &= \iint\limits_D \dfrac{−2x−2y+1}{\sqrt{1+4x^ 2 +4y^ 2}}\sqrt{1+4x^ 2 +4y^ 2}\, d A \\[4pt] \nonumber &= \iint\limits_D (−2x−2y+1)\,d A, \text{ so switching to polar coordinates gives} \\[4pt] \nonumber &=\int_0^{2\pi} \int_0^1 (−2r \cos θ −2r \sin θ +1)\,r \,dr\, dθ \\[4pt] \nonumber &=\int_0^{2\pi} \int_0^1 (−2r^ 2 \cos θ −2r^ 2 \sin θ + r)\,dr\, dθ \\[4pt] \nonumber &=\int_0^{2\pi} \left (− \dfrac{2r^ 3}{ 3} \cos θ − \dfrac{2r^ 3}{ 3} \sin θ + \dfrac{r^ 2}{ 2} \Big |_{r=0}^{r=1} \right ) \,dθ \\[4pt] \nonumber &= \int_0^{2\pi} \left ( − \dfrac{2}{ 3} \cos θ − \dfrac{2}{ 3} \sin θ + \dfrac{1}{ 2} \right ) \, dθ \\[4pt] \nonumber &= − \dfrac{2}{ 3} \sin θ +\dfrac{2}{ 3} \cos θ + \dfrac{1}{ 2} θ \Big |_0^{2\pi} = \pi . \\[4pt] \end{align}\]

La curva límite\(C\) es el círculo unitario que se\(x^ 2 + y^ 2 = 1\) coloca en el plano\(z = 1\) (ver Figura 4.5.5), que se puede parametrizar como\(x = \cos t, y = \sin t, z = 1 \text{ for }0 ≤ t ≤ 2π\). Entonces

\[\nonumber \begin{align} \oint_C \textbf{f}\cdot d\textbf{r} &= \int_0^{2\pi} ((1)(−\sin t)+(\cos t)(\cos t)+(\sin t)(0))\,dt \\[4pt] \nonumber &= \int_0^{2\pi} \left ( −\sin t+ \dfrac{1+\cos 2t}{ 2} \right ) \,dt \quad \left ( \text{here we used } \cos^2 t = \dfrac{1+\cos 2t}{ 2} \right ) \\[4pt] \nonumber &= \cos t+ \dfrac{t}{ 2} + \dfrac{\sin 2t}{ 4}\Big |_0^{2\pi} = π . \\[4pt] \end{align}\]

Entonces vemos eso\(\oint_C \textbf{f}\cdot d\textbf{r} =\iint\limits_Σ (\text{curl }\textbf{f})\cdot \textbf{n}dσ\), como lo predice el Teorema de Stokes.

La integral de línea en el ejemplo anterior era mucho más sencilla de calcular que la integral de superficie, pero no siempre será así.

Ejemplo\(\PageIndex{4}\)

Dejar\(Σ\) ser el paraboloide elíptico\(z =\dfrac{x^ 2}{ 4} + \dfrac{y^ 2}{ 9} \text{ for }z ≤ 1\), y dejar\(C\) ser su curva límite. Calcular\( \oint_C \textbf{f}\cdot d\textbf{r}\text{ for }\textbf{f}(x, y, z) = (9xz + 2y)\textbf{i} + (2x + y^ 2 )\textbf{j} + (−2y^ 2 + 2z)\textbf{k}\), donde\(C\) se atraviesa en sentido antihorario

Solución

La superficie es similar a la del Ejemplo\(\PageIndex{3}\), excepto que ahora la curva límite\(C\) es la elipse\(\dfrac{x^ 2}{ 4} + \dfrac{y^ 2}{ 9} = 1\) tendida en el plano\(z = 1\). En este caso, usar el Teorema de Stokes es más fácil que computar la integral de línea directamente. Como en el Ejemplo 4.14, en cada punto\((x, y, z(x, y))\) de la superficie\(z = z(x, y) = \dfrac{x^ 2}{ 4} + \dfrac{y^ 2}{ 9}\) el vector

\[\nonumber \textbf{n} = \dfrac{-\dfrac{∂z}{ ∂x}\textbf{i}− \dfrac{∂z}{ ∂y}\textbf{j}+\textbf{k}}{\sqrt{1 + \left ( \dfrac{∂z}{ ∂x} \right )^2 + \left ( \dfrac{∂z}{ ∂y}\right )^2}}=\dfrac{− \dfrac{x}{ 2}\textbf{i}− \dfrac{2y}{ 9}\textbf{j}+\textbf{k}}{\sqrt{1+ \dfrac{x^ 2}{ 4} + \dfrac{4y^ 2}{ 9}}},\]

es un vector normal de unidad positiva a\(Σ\). Y calculando el rizo de f da

\[\nonumber \text{curl }\textbf{f} = (−4y−0)\textbf{i} + (9x−0)\textbf{j} + (2−2)\textbf{k} = −4y\textbf{i} + 9x\textbf{j} + 0\textbf{k} ,\]

por lo

\[\nonumber (\text{curl }\textbf{f})\cdot \textbf{n} = \dfrac{(−4y)(− \dfrac{x}{ 2} )+(9x)(− \dfrac{2y}{ 9} )+(0)(1)}{\sqrt{1+ \dfrac{x^ 2}{ 4} + \dfrac{4y^ 2}{ 9}}} = \dfrac{2x y−2x y+0}{\sqrt{1+ \dfrac{x^ 2}{ 4} + \dfrac{4y^ 2}{ 9}}} = 0,\]

y así por el Teorema de Stokes

\[\nonumber \oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_Σ (\text{curl }\textbf{f})\cdot \textbf{n}\,dσ = \iint\limits_Σ 0\, dσ = 0.\]

En aplicaciones físicas, para una curva cerrada simple\(C\) la línea integral a menudo\(\oint_C \textbf{f}\cdot d\textbf{r}\) se llama la circulación de f alrededor\(C\). Por ejemplo, si E representa el campo electrostático debido a una carga puntual, entonces resulta que se riza\(\textbf{E}= \textbf{0}\), lo que significa que la circulación\(\oint_C \textbf{E}\cdot d\textbf{r} = 0\) por el Teorema de Stokes. Los campos vectoriales que tienen rizo cero a menudo se denominan campos irrotacionales.

De hecho, el término rizo fue creado por el físico escocés del siglo XIX James Clerk Maxwell en su estudio del electromagnetismo, donde se usa ampliamente. En física, el rizo se interpreta como una medida de la densidad de circulación. Esto se ve mejor usando otra definición de curl f que es equivalente a la definición dada por la ecuación\ ref {Eq4.46}. Es decir, por un punto\((x, y, z) \text{ in }\mathbb{R}^ 3\),

\[\textbf{n}\cdot (\text{curl }\textbf{f}(x, y, z) = \lim\limits_{S \to 0} \dfrac{1}{S}\oint_C \textbf{f}\cdot d\textbf{r},\label{Eq4.50}\]

donde\(S\) es el área superficial de una superficie\(Σ\) que contiene el punto\((x, y, z)\) y con una curva límite cerrada simple\(C\) y el vector normal unitario positivo n at\((x, y, z)\). En el límite, piense en la curva que\(C\) se encoge hasta el punto\((x, y, z)\)\(Σ\), lo que provoca que la superficie que limita tenga una superficie cada vez más pequeña. Esa relación de circulación a superficie en el límite es lo que hace que el rizo sea una medida aproximada de la densidad de circulación (es decir, circulación por unidad de área).

Figura 4.5.6 Curl y rotación

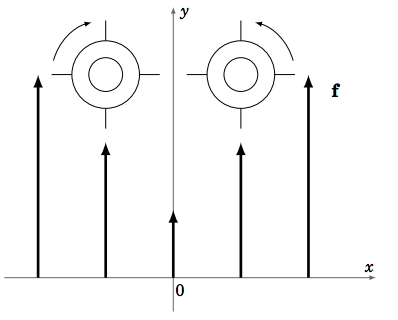
En la Figura 4.5.6 se muestra una idea de cómo se relaciona el rizo de un campo vectorial con la rotación. Supongamos que tenemos un campo vectorial\(\textbf{f}(x, y, z)\) que siempre es paralelo al\(x y\) plano -en cada punto\((x, y, z)\) y que los vectores crecen más grande cuanto más lejos\((x, y, z)\) está el punto\(y\) del eje. Por ejemplo,\(\textbf{f}(x, y, z) = (1+ x^ 2 )\textbf{j}\). Piense en el campo vectorial como que representa el flujo de agua, e imagine caer dos ruedas con paletas en ese flujo de agua, como en la Figura 4.5.6. Dado que el flujo es más fuerte (es decir, la magnitud de f es mayor) a medida que se aleja del\(y\) eje -eje, entonces dicha rueda giraría en sentido antihorario si se dejara caer a la derecha del\(y\) eje -y giraría en el sentido de las agujas del reloj si se dejara caer a la izquierda del\(y\) eje -eje. En ambos casos el rizo sería distinto de cero (curl\(\textbf{f}(x, y, z) = 2x\textbf{k}\) en nuestro ejemplo) y obedecería la regla de la derecha, es decir, los\(\textbf{f}(x, y, z)\) puntos de rizo en la dirección de tu pulgar a medida que cobras tu mano derecha en la dirección de la rotación de la rueda. Entonces el curl apunta hacia afuera (en la\(z\) dirección positiva) if\(x > 0\) y apunta hacia adentro (en la\(z\) dirección negativa) if\(x < 0\). Observe que si todos los vectores tuvieran la misma dirección y la misma magnitud, entonces las ruedas no girarían y de ahí no habría rizo (razón por la cual tales campos se llaman irrotacionales, es decir, no hay rotación).

Finalmente, por el Teorema de Stokes, sabemos que si\(C\) es una simple curva cerrada en alguna región sólida\(S\) en\(\mathbb{R}^ 3\) y si\(\textbf{f}(x, y, z)\) es un campo vectorial suave tal que rizo\(\textbf{f} = 0 \text{ in }S\), entonces

\[\nonumber \oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_Σ (\text{curl }\textbf{f}\cdot \textbf{n}\,dσ = \iint\limits_Σ \textbf{0}\cdot \textbf{n}\, dσ = \iint\limits_Σ 0\,dσ = 0,\]

donde\(Σ\) está cualquier superficie orientable dentro\(S\) cuyo límite esté\(C\) (tal superficie a veces se llama superficie de tapado para\(C\)). Tan similar al caso de dos variables, tenemos una versión tridimensional de un resultado de la Sección 4.3, para regiones sólidas en las\(\mathbb{R}^ 3\) que simplemente están conectadas (es decir, regiones que no tienen agujeros):

Las siguientes declaraciones son equivalentes para una región sólida simplemente conectada\(S\) en\(\mathbb{R}^ 3\):

1. \(\textbf{f}(x, y, z) = P(x, y, z)\textbf{i}+Q(x, y, z)\textbf{j}+ R(x, y, z)\textbf{k}\)tiene un potencial suave\(F(x, y, z) \text{ in }S\)
2. \(\int_C \textbf{f}\cdot d\textbf{r}\)es independiente de la trayectoria para cualquier curva\(C\) en\(S\)
3. \(\oint_C \textbf{f}\cdot d\textbf{r} = 0\)para cada curva cerrada simple\(C\) en\(S\)
4. \(\dfrac{∂R}{ ∂y} = \dfrac{∂Q}{ ∂z} , \dfrac{∂P}{ ∂z} = \dfrac{∂R}{ ∂x} , \text{ and }\dfrac{∂Q}{ ∂x} = \dfrac{∂P}{ ∂y}\)en\(S\) (es decir, rizo\(\textbf{f} = \textbf{0} \text{ in }S\))

La parte d) es también una manera de decir que la forma diferencial\(P \,dx+Q \,d y+ R\, dz\) es exacta.

Ejemplo\(\PageIndex{5}\)

Determinar si el campo vectorial\(\textbf{f}(x, y, z) = x yz \textbf{i}+xz \textbf{j}+x y\textbf{k}\) tiene un potencial en\(\mathbb{R}^ 3\).

Solución

Ya que\(\mathbb{R}^ 3\) está simplemente conectado, solo necesitamos verificar si curl f = 0 a lo largo\(\mathbb{R}^ 3\), es decir,

\[\nonumber \dfrac{∂R}{ ∂y} = \dfrac{∂Q}{ ∂z} ,\quad \dfrac{∂P}{ ∂z} = \dfrac{∂R}{ ∂x} ,\quad \text{and }\dfrac{∂Q}{ ∂x} = \dfrac{∂P}{ ∂y} \]

en todo\(\mathbb{R}^ 3\), donde\(P(x, y, z) = x yz, Q(x, y, z) = xz, \text{ and }R(x, y, z) = x y\). Pero vemos que

\[\nonumber \dfrac{∂P}{ ∂z} = x y ,\, \dfrac{∂R}{ ∂x} = y \quad \Rightarrow \quad \dfrac{∂P}{ ∂z} \neq \dfrac{∂R}{ ∂x} \text{ for some }(x, y, z) \text{ in }\mathbb{R}^ 3 .\]

Por lo tanto,\(f(x, y, z)\) no tiene un potencial en\(\mathbb{R}^ 3\).

Colaboradores y Atribuciones

• Template:ContribCorral