4.6: Gradiente, divergencia, rizo y laplaciano
- Page ID
- 111300
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección final estableceremos algunas relaciones entre el gradiente, la divergencia y el rizo, y también introduciremos una nueva cantidad llamada laplaciana. A continuación, mostraremos cómo escribir estas cantidades en coordenadas cilíndricas y esféricas.
Gradiente
Para una función de valor real\(f (x, y, z)\) on\(\mathbb{R}^ 3\), el gradiente\(∇f (x, y, z)\) es una función de valor vectorial on\(\mathbb{R}^ 3\), es decir, su valor en un punto\((x, y, z)\) es el vector
\[\nonumber ∇f (x, y, z) = \left ( \dfrac{∂f}{ ∂x} , \dfrac{∂f}{ ∂y} , \dfrac{∂f}{ ∂z} \right ) = \dfrac{∂f}{ ∂x}\textbf{i} + \dfrac{∂f}{ ∂y}\textbf{j} + \dfrac{∂f}{ ∂z}\textbf{k} \]
en\(\mathbb{R}^ 3\), donde cada una de las derivadas parciales es evaluada en el punto\((x, y, z)\). Entonces de esta manera, se puede pensar en el símbolo\(∇\) como “aplicado” a una función de valor real\(f\) para producir un vector\(∇f\).
Resulta que la divergencia y el rizo también se pueden expresar en términos del símbolo\(∇\). Esto se hace pensando en\(∇\) como un vector en\(\mathbb{R}^ 3\), a saber
\[∇ = \dfrac{∂}{ ∂x}\textbf{i} + \dfrac{∂}{ ∂y}\textbf{j} + \dfrac{∂}{ ∂z}\textbf{k} .\label{Eq4.51}\]
Aquí, los símbolos deben ser\(\dfrac{∂}{ ∂x} ,\, \dfrac{∂}{∂y} \text{ and }\dfrac{∂}{ ∂z}\) pensados como “operadores derivados parciales” que se “aplicarán” a una función de valor real, digamos\(f (x, y, z)\), para producir las derivadas parciales\(\dfrac{∂f}{ ∂x} ,\, \dfrac{ ∂f}{ ∂y}\text{ and }\dfrac{∂f}{ ∂z}\). Por ejemplo,\(\dfrac{∂}{ ∂x}\) “aplicado” a\(f (x, y, z) \text{ produces }\dfrac{∂f}{ ∂x}\).
¿\(∇\)Realmente es un vector? Estrictamente hablando, no, ya que no\(\dfrac{∂}{ ∂x} ,\, \dfrac{∂}{ ∂y} \text{ and }\dfrac{∂}{ ∂z}\) son números reales. Pero ayuda pensar en un vector, sobre todo con la divergencia y el rizo, como pronto veremos.\(∇\) El proceso de “aplicar”\(\dfrac{∂}{ ∂x} ,\, \dfrac{∂}{ ∂y} ,\, \dfrac{∂}{ ∂z}\) a una función de valor real normalmente\(f (x, y, z)\) se considera multiplicando las cantidades:
\[\nonumber \left ( \dfrac{∂}{ ∂x} \right ) (f ) = \dfrac{∂f}{ ∂x},\, \left ( \dfrac{∂}{ ∂y} \right ) (f ) = \dfrac{∂f}{ ∂y} ,\, \left ( \dfrac{∂}{ ∂z} \right ) (f ) = \dfrac{∂f}{ ∂z}\]
Por esta razón, a menudo\(∇\) se le conoce como el “del operator”, ya que “opera” en funciones.
Divergencia
Por ejemplo, a menudo es conveniente escribir la divergencia div f como\(∇ \cdot \textbf{f}\), ya que para un campo vectorial\(\textbf{f}(x, y, z) = f_1(x, y, z)\textbf{i}+ f_2(x, y, z)\textbf{j}+ f_3(x, y, z)\textbf{k}\), el producto punto de f with\(∇\) (pensado como un vector) tiene sentido:
\[\nonumber \begin{align} ∇·\textbf{f} &= \left ( \dfrac{∂}{ ∂x}\textbf{i} + \dfrac{∂}{ ∂y}\textbf{j} + \dfrac{∂}{ ∂z}\textbf{k} \right ) · (f_1(x, y, z)\textbf{i} + f_2(x, y, z)\textbf{j} + f_3(x, y, z)\textbf{k}) \\[4pt] \nonumber &= \left ( \dfrac{∂}{ ∂x} \right ) (f_1) + \left ( \dfrac{∂}{ ∂y} \right ) (f_2) + \left ( \dfrac{∂}{ ∂z} \right ) (f_3) \\[4pt] \nonumber &= \dfrac{∂f_1}{ ∂x} + \dfrac{∂f_2}{ ∂y} + \dfrac{∂f_3}{ ∂z} \\[4pt] \nonumber &= \text{div }\textbf{f} \\[4pt] \end{align}\]
También podemos escribir curl f en términos de\(∇\), es decir, como\(∇ × \textbf{f}\), ya que para un campo vectorial\(\textbf{f}(x, y, z) = P(x, y, z)\textbf{i}+Q(x, y, z)\textbf{j}+ R(x, y, z)\textbf{k}\), tenemos:
\[\nonumber \begin{align} ∇ × \textbf{f} &= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\[4pt] \dfrac{∂}{ ∂x} & \dfrac{∂}{ ∂y} & \dfrac{∂}{ ∂z} \\[4pt] \nonumber P(x, y, z) & Q(x, y, z) & R(x, y, z) \\[4pt] \end{vmatrix} \\[4pt] \nonumber &=\left ( \dfrac{∂R}{ ∂y} − \dfrac{∂Q}{ ∂z}\right )\textbf{i} − \left ( \dfrac{∂R}{ ∂x} − \dfrac{∂P}{ ∂z} \right )\textbf{j} + \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right )\textbf{k} \\[4pt] \nonumber &= \left ( \dfrac{∂R}{ ∂y} − \dfrac{∂Q}{ ∂z}\right )\textbf{i} + \left (\dfrac{∂P}{ ∂z}-\dfrac{∂R}{ ∂x} \right )\textbf{j} + \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right )\textbf{k} \\[4pt] \nonumber &=\text{curl }\textbf{f} \\[4pt] \end{align}\]
Para una función de valor real\(f (x, y, z)\), el gradiente\(∇f (x, y, z) = \dfrac{∂f}{ ∂x}\textbf{i} + \dfrac{∂f}{ ∂y}\textbf{j} + \dfrac{∂f}{ ∂z}\textbf{k}\) es un campo vectorial, por lo que podemos tomar su divergencia:
\[\nonumber \begin{align} \text{div }∇f &= ∇· ∇f \\[4pt] \nonumber &=\left ( \dfrac{∂}{ ∂x}\textbf{i} + \dfrac{∂}{ ∂y}\textbf{j} + \dfrac{∂}{ ∂z}\textbf{k} \right ) · \left ( \dfrac{∂f}{ ∂x}\textbf{i} + \dfrac{∂f}{ ∂y}\textbf{j} + \dfrac{∂f}{ ∂z}\textbf{k} \right ) \\[4pt] \nonumber &=\dfrac{∂}{ ∂x} \left ( \dfrac{∂f}{ ∂x} \right ) + \dfrac{∂}{ ∂y} \left ( \dfrac{∂f}{ ∂y} \right ) + \dfrac{∂}{ ∂z} \left ( \dfrac{∂f}{ ∂z} \right ) \\[4pt] \nonumber &= \dfrac{∂^2 f}{ ∂x^ 2} + \dfrac{∂^ 2 f}{ ∂y^ 2} + \dfrac{∂^ 2 f}{ ∂z^ 2} \\[4pt] \end{align}\]
Tenga en cuenta que esta es una función de valor real, a la que le daremos un nombre especial:
Definición 4.7: Laplaciana
Para una función de valor real\(f (x, y, z)\), el laplaciano de\(f\), denotado por\(∆f\), viene dado por
\[∆f (x, y, z) = ∇· ∇f = \dfrac{∂^ 2 f}{ ∂x^ 2} + \dfrac{∂^ 2 f}{ ∂y^ 2} + \dfrac{∂^ 2 f}{ ∂z^ 2} .\label{Eq4.52}\]
A menudo la notación\(∇^2 f\) se usa para los laplacianos en lugar de\(∆f\), usando la convención\(∇^ 2 = ∇· ∇\).
Ejemplo 4.17
Let\(\textbf{r}(x, y, z) = x\textbf{i}+y\textbf{j}+z\textbf{k}\) Ser el campo de vector de posición en\(\mathbb{R}^ 3\). Entonces\(\lVert \textbf{r}(x, y, z)\rVert ^2 = \textbf{r} · \textbf{r} = x^ 2 + y^ 2 + z^ 2\) es una función de valor real. Encuentra
- el gradiente de\(\lVert \textbf{r} \rVert ^2\)
- la divergencia de\(\textbf{r}\)
- el rizo de\(\textbf{r}\)
- el Laplaciano de\(\lVert \textbf{r} \rVert ^2\)
Solución:
(a)\(∇ \rVert \textbf{r}\rVert ^2 = 2x\textbf{i}+2y\textbf{j}+2z\textbf{k} = 2\textbf{r}\)
b)\(∇· \textbf{r} = \dfrac{∂}{ ∂x} (x)+ \dfrac{∂}{ ∂y} (y)+ \dfrac{∂}{ ∂z} (z) = 1+1+1 = 3\)
c)
\[\nonumber ∇ × \textbf{r} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\[4pt] \dfrac{∂}{ ∂x} & \dfrac{∂}{ ∂y} & \dfrac{∂}{ ∂z} \\[4pt] x & y & z \\[4pt] \end{vmatrix} = (0−0)\textbf{i} − (0−0)\textbf{j} + (0−0)\textbf{k} = \textbf{0} \]
d)\(∆ \lVert \textbf{r} \rVert ^2 = \dfrac{∂^ 2}{ ∂x^ 2} (x^ 2 + y^ 2 + z^ 2 )+ \dfrac{∂^ 2}{ ∂y^ 2} (x^ 2 + y^ 2 + z^ 2 )+ \dfrac{∂^ 2}{ ∂z^ 2} (x^ 2 + y^ 2 + z^ 2 ) = 2+2+2 = 6\)
Tenga en cuenta que podríamos haber calculado de\(∆\lVert \textbf{r} \rVert ^2\) otra manera, usando la\(∇\) notación junto con las partes (a) y (b):
\[\nonumber ∆\lVert \textbf{r} \rVert ^2 = ∇· ∇ \lVert \textbf{r} \rVert ^2 = ∇· 2\textbf{r} = 2∇· \textbf{r} = 2(3) = 6\]
Observe que en el Ejemplo 4.17 si tomamos el rizo del gradiente de\(\lVert \textbf{r} \rVert ^2\) obtenemos
\[\nonumber ∇ × (∇ \rVert \textbf{r}\rVert ^2 ) = ∇ × 2\textbf{r} = 2∇ × \textbf{r} = 2\textbf{0} = \textbf{0} .\]
El siguiente teorema muestra que este será el caso en general:
Teorema 4.15.
Para cualquier función fluida de valor real\(f (x, y, z), ∇ × (∇f ) = \textbf{0}\).
Prueba
Vemos por la suavidad de f que
\[\begin{align} ∇ × (∇f ) &= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\[4pt] \dfrac{∂}{ ∂x} & \dfrac{∂}{ ∂y} & \dfrac{∂}{ ∂z} \\[4pt] \dfrac{∂f}{ ∂x} & \dfrac{∂f}{ ∂y} & \dfrac{∂f}{ ∂z} \\[4pt] \end{vmatrix} \\[4pt] &= \left ( \dfrac{∂^ 2 f}{ ∂y∂z} − \dfrac{∂^ 2 f}{ ∂z∂y} \right )\textbf{i} − \left ( \dfrac{∂^ 2 f}{ ∂x∂z} − \dfrac{∂^ 2 f}{ ∂z∂x} \right )\textbf{j} + \left ( \dfrac{∂^ 2 f}{ ∂x∂y} − \dfrac{∂^ 2 f}{ ∂y∂x} \right )\textbf{k} = \textbf{0} ,\\[4pt] \end{align}\]
ya que las derivadas parciales mixtas en cada componente son iguales.
\(\square\)
Corolario 4.16
Si un campo vectorial\(f(x, y, z)\) tiene un potencial, entonces rizar\(\textbf{f} = \textbf{0}\).
Otra forma de afirmar el Teorema 4.15 es que los gradientes son irrotacionales. Además, observe que en el Ejemplo 4.17 si tomamos la divergencia del rizo de r obtenemos trivialmente
\[∇· (∇ × \textbf{r}) = ∇· \textbf{0} = 0 .\]
El siguiente teorema muestra que este será el caso en general:
Teorema 4.17.
Para cualquier campo vectorial suave\(\textbf{f}(x, y, z), ∇· (∇ × \textbf{f}) = 0.\)
La prueba es directa y se deja como un ejercicio para el lector.
Corolario 4.18
El flujo del rizo de un campo vectorial liso\(f(x, y, z)\) a través de cualquier superficie cerrada es cero.
Prueba: Dejar\(Σ\) ser una superficie cerrada que limita un sólido\(S\). El flujo de\(∇ × \textbf{f}\) a través\(Σ\) es
\[\begin{align} \iint\limits_Σ (∇ × \textbf{f})· dσ &= \iiint\limits_S ∇· (∇ × \textbf{f})\, dV \text{ (by the Divergence Theorem)} \\[4pt] &= \iiint\limits_S 0\, dV \text{ (by Theorem 4.17)} \\[4pt] &= 0 \\[4pt] \end{align}\]
\(\tag{\(\textbf{QED}\)}\)
Existe otro método para probar el Teorema 4.15 que puede ser útil, y se utiliza a menudo en la física. Es decir, si la superficie integral\(\iint\limits_Σ f (x, y, z)\,dσ = 0\) para todas las superficies\(Σ\) en alguna región sólida (generalmente todas\(\mathbb{R}^ 3\)), entonces debemos tener\(f (x, y, z) = 0\) en toda esa región. La prueba no es trivial, y los físicos no suelen molestarse en demostrarlo. Pero el resultado es cierto, y también se puede aplicar a integrales dobles y triples.
Por ejemplo, para probar el Teorema 4.15, supongamos que\(f (x, y, z)\) es una función fluida de valor real en\(\mathbb{R}^ 3\). Dejar\(C\) ser una simple curva cerrada en\(\mathbb{R}^ 3\) y dejar\(Σ\) ser cualquier superficie de tapado para\(C\) (es decir,\(Σ\) es orientable y su límite es\(C\)). Dado que\(∇f\) es un campo vectorial, entonces
\[\nonumber \begin{align} \iint\limits_Σ (∇ × (∇f ))· \textbf{n}\,dσ &= \oint_C ∇f · d\textbf{r} \text{ by Stokes’ Theorem, so} \\[4pt] \nonumber &= 0 \text{ by Corollary 4.13.} \\[4pt] \end{align}\]
Dado que la elección de\(Σ\) fue arbitraria, entonces debemos tener\((∇×(∇f ))·\textbf{n} = 0\) a lo largo\(\mathbb{R}^ 3\), donde n es cualquier vector unitario. Usando i, j y k en lugar de n, vemos que debemos tener\(∇ × (∇f ) = \textbf{0}\) en\(\mathbb{R}^ 3\), lo que completa la prueba.
Ejemplo 4.18
Un sistema de cargas eléctricas tiene una densidad de carga\(ρ(x, y, z)\) y produce un campo electrostático\(\textbf{E}(x, y, z)\)\((x, y, z)\) en puntos del espacio. La Ley de Gauss establece que
\[\nonumber \iint\limits_Σ \textbf{E}· dσ = 4π \iiint\limits_S ρ \,dV\]
para cualquier superficie cerrada\(Σ\) que encierra las cargas,\(S\) siendo la región sólida encerrada por\(Σ\). \(∇· \textbf{E} = 4πρ\)Demuéstralo. Esta es una de las Ecuaciones de Maxwell.
Solución
Por el Teorema de la Divergencia, tenemos
\[\nonumber \begin{align} \iiint\limits_S ∇· \textbf{E} dV &= \iint\limits_Σ \textbf{E}· dσ \\[4pt] \nonumber &= 4π \iiint\limits_S ρ \,dV \text{ by Gauss’ Law, so combining the integrals gives} \\[4pt] \nonumber \iiint\limits_S (∇· \textbf{E}−4πρ) \,dV &= 0 \text{ , so} \\[4pt] \nonumber ∇· \textbf{E}−4πρ &= 0 \text{ since }Σ \text{ and hence } S \text{ was arbitrary, so} \\[4pt] \nonumber ∇· \textbf{E} &= 4πρ. \\[4pt] \end{align}\]
A menudo (especialmente en física) es conveniente utilizar otros sistemas de coordenadas cuando se trata de cantidades como el gradiente, divergencia, rizo y laplaciano. Presentaremos las fórmulas para estos en coordenadas cilíndricas y esféricas.
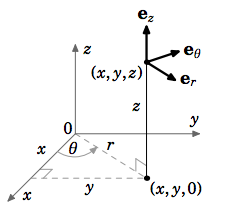
Recordemos de la Sección 1.7 que un punto se\((x, y, z)\) puede representar en coordenadas cilíndricas\((r,θ, z), \text{ where }x = r \cos θ , y = r \sin θ, z = z.\) En cada punto\((r,θ, z), \text{ let }\textbf{e}_r, \textbf{e}_θ, \textbf{e}_z \text{ be unit vectors in the direction of increasing }r, θ, z,\) respectivamente (ver Figura 4.6.1). Después\(\textbf{e}_r, \textbf{e}_θ, \textbf{e}_z\) formar un conjunto ortonormal de vectores. Obsérvese, por la regla de la derecha, que\(\textbf{e}_z × \textbf{e}_r = \textbf{e}_θ.\)
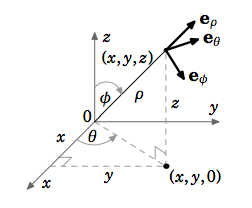
De igual manera, un punto se\((x, y, z)\) puede representar en coordenadas esféricas\((ρ,θ,φ)\), donde\(x = ρ \sin φ \cos θ, y = ρ \sin φ \sin θ, z = ρ \cos φ.\) En cada punto\((ρ,θ,φ)\), dejan\(\textbf{e}_ρ, \textbf{e}_θ, \textbf{e}_φ\) ser vectores unitarios en la dirección de incremento\(ρ, θ, φ\), respectivamente (ver Figura 4.6.2). Entonces los vectores\(\textbf{e}_ρ, \textbf{e}_θ, \textbf{e}_φ\) son ortonormales. Por la regla de la mano derecha, eso lo vemos\(\textbf{e}_θ × \textbf{e}_ρ = \textbf{e}_φ\).
Ahora podemos resumir las expresiones para el gradiente, divergencia, rizo y Laplaciano en coordenadas cartesianas, cilíndricas y esféricas en las siguientes tablas:
Cartesiano
\((x, y, z)\): Función escalar\(F\); Campo vectorial\(\textbf{f} = f_1 \textbf{i}+ f_2 \textbf{j}+ f_3\textbf{k}\)
- gradiente:\(∇F = \dfrac{∂F}{ ∂x}\textbf{i} + \dfrac{∂F}{ ∂y}\textbf{j} + \dfrac{∂F}{ ∂z}\textbf{k}\)
- divergencia:\(∇·\textbf{f} = \dfrac{∂f_1}{ ∂x} + \dfrac{∂f_2}{ ∂y} + \dfrac{∂f_3}{ ∂z}\)
- rizo:\(∇ × \textbf{f} = \left ( \dfrac{∂f_3}{ ∂y} − \dfrac{∂f_2}{ ∂z} \right ) \textbf{i} + \left ( \dfrac{∂f_1}{ ∂z} − \dfrac{∂f_3}{ ∂x} \right ) \textbf{j} + \left ( \dfrac{∂f_2}{ ∂x} − \dfrac{∂f_1}{ ∂y} \right )\textbf{k}\)
- Laplaciano:\(∆F = \dfrac{∂^ 2F}{ ∂x^ 2} + \dfrac{∂^ 2F}{ ∂y^ 2} + \dfrac{∂^ 2F}{ ∂z^ 2}\)
cilíndrico
\((r,θ, z)\): Función escalar\(F\); Campo vectorial\(\textbf{f} = f_r \textbf{e}_r + f_θ \textbf{e}_θ + f_z \textbf{e}_z\)
- gradiente:\(∇F = \dfrac{∂F}{ ∂r} \textbf{e}_r + \dfrac{1}{ r}\dfrac{ ∂F}{ ∂θ} \textbf{e}_θ + \dfrac{∂F}{ ∂z} \textbf{e}_z\)
- divergencia:\(∇·\textbf{f} = \dfrac{1}{ r}\dfrac{ ∂}{ ∂r} (r f_r) + \dfrac{1}{ r} \dfrac{∂f_θ}{ ∂θ} + \dfrac{∂f_z}{ ∂z}\)
- rizo:\(∇ × \textbf{f} = \left ( \dfrac{1}{ r} \dfrac{∂f_z}{ ∂θ} − \dfrac{∂f_θ}{ ∂z} \right ) \textbf{e}_r + \left ( \dfrac{∂f_r}{ ∂z} − \dfrac{∂f_z}{ ∂r} \right ) \textbf{e}_θ + \dfrac{1}{ r} \left ( \dfrac{∂}{ ∂r} (r f_θ)− \dfrac{∂f_r}{ ∂θ}\right ) \textbf{e}_z\)
- Laplaciano:\(∆F = \dfrac{1}{ r}\dfrac{ ∂}{ ∂r} \left ( r \dfrac{∂F}{ ∂r} \right ) + \dfrac{1}{ r^2} \dfrac{∂^ 2F}{ ∂θ^2} + \dfrac{∂^ 2F}{ ∂z^ 2}\)
Esférico
\((ρ,θ,φ)\): Función escalar\(F\); Campo vectorial\(\textbf{f} = f_ρ \textbf{e}_ρ + f_θ \textbf{e}_θ + f_φ \textbf{e}_φ\)
- gradiente:\(∇F = \dfrac{∂F}{ ∂ρ} \textbf{e}_ρ + \dfrac{1}{ ρ \sin φ} \dfrac{∂F}{ ∂θ} \textbf{e}_θ + \dfrac{1}{ ρ}\dfrac{ ∂F}{ ∂φ} \textbf{e}_φ\)
- divergencia:\(∇·\textbf{f} = \dfrac{1}{ ρ^ 2} \dfrac{∂}{ ∂ρ} (ρ^ 2 f_ρ) + \dfrac{1}{ ρ} \sin φ \dfrac{∂f_θ}{ ∂θ} + \dfrac{1}{ ρ \sin φ} \dfrac{∂}{ ∂φ} (\sin φ f_θ)\)
- rizo:\(∇ × \textbf{f} = \dfrac{1}{ ρ \sin φ} \left ( \dfrac{∂}{ ∂φ} (\sin φ f_θ)− \dfrac{∂f_φ}{ ∂θ} \right ) \textbf{e}_ρ + \dfrac{1}{ ρ} \left ( \dfrac{∂}{ ∂ρ} (ρ f_φ)− \dfrac{∂f_ρ}{ ∂φ} \right ) \textbf{e}_θ + \left ( \dfrac{1}{ ρ \sin φ} \dfrac{∂f_ρ}{ ∂θ} − \dfrac{1}{ ρ} \dfrac{∂}{ ∂ρ} (ρ f_θ) \right ) \textbf{e}_φ\)
- Laplaciano:\(∆F = \dfrac{1}{ ρ^ 2} \dfrac{∂}{ ∂ρ} \left ( ρ^ 2 \dfrac{∂F}{ ∂ρ} \right ) + \dfrac{1}{ ρ^ 2 \sin^2 φ} \dfrac{∂^ 2F}{ ∂θ^2} + \dfrac{1}{ ρ^ 2 \sin φ} \dfrac{∂}{ ∂φ} \left ( \sin φ \dfrac{∂F}{ ∂φ}\right ) \)
La derivación de las fórmulas anteriores para coordenadas cilíndricas y esféricas es sencilla pero extremadamente tediosa. La idea básica es tomar el equivalente cartesiano de la cantidad en cuestión y sustituirlo en esa fórmula utilizando la transformación de coordenadas apropiada. Como ejemplo, derivaremos la fórmula para el gradiente en coordenadas esféricas.
Objetivo: Mostrar que el gradiente de una función de valor real\(F(ρ,θ,φ)\) en coordenadas esféricas es:
\[\nonumber ∇F = \dfrac{∂F}{ ∂ρ} \textbf{e}_ρ + \dfrac{1}{ ρ \sin φ} \dfrac{∂F}{ ∂θ} \textbf{e}_θ +\dfrac{1}{ ρ}\dfrac{ ∂F}{ ∂φ}\textbf{e}_φ\]
Idea: En la fórmula del gradiente cartesiano\(∇F(x, y, z) = \dfrac{∂F}{ ∂x}\textbf{i}+ \dfrac{∂F}{ ∂y}\textbf{j}+ \dfrac{∂F}{ ∂z}\textbf{k}\), poner los vectores de base cartesiana i, j, k en términos de los vectores de base de coordenadas esféricas\(\textbf{e}_ρ, \textbf{e}_θ, \textbf{e}_φ\) y funciones de\(ρ, θ \text{ and }φ\). Entonces poner las derivadas parciales\(\dfrac{∂F}{ ∂x} , \dfrac{∂F}{ ∂y} , \dfrac{∂F}{ ∂z}\) en términos de\(\dfrac{∂F}{ ∂ρ} , \dfrac{∂F}{ ∂θ} , \dfrac{∂F}{ ∂φ}\) y funciones de\(ρ, θ \text{ and }φ\).
Paso 1: Obtener fórmulas para\(\textbf{e}_ρ, \textbf{e}_θ, \textbf{e}_φ\) en términos de i, j, k.
Podemos ver en la Figura 4.6.2 que el vector unitario\(\textbf{e}_ρ\) en la\(ρ\) dirección en un punto general\((ρ,θ,φ)\)\(\textbf{e}_ρ = \dfrac{\textbf{r}}{ \lVert \textbf{r} \rVert } , \text{ where }\textbf{r} = x\textbf{i} + y\textbf{j} + z\textbf{k}\) es el vector de posición del punto en coordenadas cartesianas. Por lo tanto,
\[\nonumber \textbf{e}_ρ = \dfrac{\textbf{r}}{ \lVert \textbf{r} \rVert} = \dfrac{x\textbf{i}+ y\textbf{j}+ z\textbf{k}}{ \sqrt{ x^ 2 + y^ 2 + z^ 2}} ,\]
así que usando\(x = ρ \sin φ \cos θ, y = ρ \sin φ \sin θ, z = ρ \cos φ, \text{ and }ρ = \sqrt{ x^ 2 + y^ 2 + z^ 2}\), obtenemos:
\[\nonumber \fbox{\(\textbf{e}_ρ = \sin φ \cos θ\textbf{i} + \sin φ \sin θ \textbf{j} + \cos φ\textbf{k}\)}\]
Ahora, dado que el ángulo\(θ\) se mide en el\(x y\) plano, entonces la\(\textbf{e}_θ \text{ in the }θ\) dirección del vector unitario debe ser paralela al\(x y\) plano. Es decir,\(\textbf{e}_θ \text{ is of the form }a\textbf{i} + b\textbf{j} + 0\textbf{k}\). Para averiguar cuáles\(a \text{ and }b\) son, tenga en cuenta que desde\(\textbf{e}_θ \perp \textbf{e}_ρ\), entonces en particular\(\textbf{e}_θ \perp \textbf{e}_ρ\) cuando\(\textbf{e}_ρ \text{ is in the }x y\) -avión. Eso ocurre cuando el ángulo\(φ \text{ is }π/2\). Poniendo\(φ = π/2\) en la fórmula para\(\textbf{e}_ρ \text{ gives }\textbf{e}_ρ = \cos θ \textbf{i}+\sin θ \textbf{j}+0\textbf{k}\), y vemos que un vector perpendicular a eso es\(−\sin θ \textbf{i}+\cos θ \textbf{j}+0\textbf{k}\). Dado que este vector es también un vector unitario y apunta en la\(θ\) dirección (positiva), debe ser\(\textbf{e}_θ\):
\[\nonumber \fbox{\(\textbf{e}_θ = −\sin θ \textbf{i} + \cos θ \textbf{j} + 0\textbf{k}\)}\]
Por último, ya\(\textbf{e}_φ = \textbf{e}_θ × \textbf{e}_ρ,\) que obtenemos:
\[\nonumber \fbox{\(\textbf{e}_φ = \cos φ \cos θ \textbf{i} + \cos φ \sin θ \textbf{j} − \sin φ\textbf{k}\)}\]
Paso 2: Usa las tres fórmulas del Paso 1 para resolver para i, j, k en términos de\(\textbf{e}_ρ, \textbf{e}_θ, \textbf{e}_φ\).
Esto se reduce a resolver un sistema de tres ecuaciones en tres incógnitas. Hay muchas formas de hacer esto, pero lo haremos combinando las fórmulas para\(\textbf{e}_ρ \text{ and }\textbf{e}_φ \text{ to eliminate }k\), lo que nos dará una ecuación que involucra solo i y j. Esto, con la fórmula para\(\textbf{e}_θ\), nos dejará entonces con un sistema de dos ecuaciones en dos incógnitas (i y j), que usaremos para resolver primero para j luego para i. Por último, resolveremos para k.
Primero, tenga en cuenta que
\[\nonumber \sin φ \textbf{e}_ρ + \cos φ \textbf{e}_φ = \cos θ \textbf{i} + \sin θ \textbf{j}\]
para que
\[\nonumber \sin θ (\sin φ \textbf{e}_ρ + \cos φ \textbf{e}_φ) + \cos θ \textbf{e}_θ = (\sin^2 θ +\cos^2 θ)\textbf{j} = \textbf{j} ,\]
y así:
\[\nonumber \fbox{\(\textbf{j} = \sin φ \sin θ \textbf{e}_ρ + \cos θ \textbf{e}_θ + \cos φ \sin θ \textbf{e}_φ\)}\]
De igual manera, vemos que
\[\nonumber \cos θ (\sin φ \textbf{e}_ρ + \cos φ \textbf{e}_φ) − \sin θ \textbf{e}_θ = (\cos^2 θ +\sin^2 θ)\textbf{i} = \textbf{i} ,\]
y así:
\[\nonumber \fbox{\(\textbf{i} = \sin φ \cos θ \textbf{e}_ρ − \sin θ \textbf{e}_θ + \cos φ \cos θ \textbf{e}_φ\)}\]
Por último, vemos que:
\[\nonumber \fbox{\(\textbf{k} = \cos φ \textbf{e}_ρ − \sin φ \textbf{e}_φ\)}\]
Paso 3: Obtener fórmulas para\(\dfrac{∂F}{ ∂ρ} , \dfrac{∂F}{ ∂θ} , \dfrac{∂F}{ ∂φ} \text{ in terms of }\dfrac{∂F}{ ∂x} , \dfrac{∂F}{ ∂y} , \dfrac{∂F}{ ∂z}\).
Por la Regla de la Cadena, tenemos
\[\nonumber \begin{align} \dfrac{∂F}{ ∂ρ} &= \dfrac{∂F}{ ∂x} \dfrac{∂x}{ ∂ρ} + \dfrac{∂F}{ ∂y}\dfrac{ ∂y}{ ∂ρ} + \dfrac{∂F}{ ∂z} \dfrac{∂z}{ ∂ρ}, \\[4pt] \nonumber \dfrac{∂F}{ ∂θ} &= \dfrac{∂F}{ ∂x} \dfrac{∂x}{ ∂θ} + \dfrac{∂F}{ ∂y} \dfrac{∂y}{ ∂θ} + \dfrac{∂F}{ ∂z} \dfrac{∂z}{ ∂θ}, \\[4pt] \nonumber \dfrac{∂F}{ ∂φ} &= \dfrac{∂F}{ ∂x} \dfrac{∂x}{ ∂φ} + \dfrac{∂F}{ ∂y} \dfrac{∂y}{ ∂φ} + \dfrac{∂F}{ ∂z} \dfrac{∂z}{ ∂φ} ,\\[4pt] \end{align}\]
que rinde:
\[\fbox{\(\nonumber \begin{align} \dfrac{∂F}{ ∂ρ} &= \sin φ \cos θ\dfrac{∂F}{ ∂x} + \sin φ \sin θ \dfrac{∂F}{ ∂y} + \cos φ \dfrac{∂F}{ ∂z} \\[4pt] \nonumber \dfrac{∂F}{ ∂θ} &= −ρ \sin φ \sin θ \dfrac{∂F}{ ∂x} + ρ \sin φ \cos θ \dfrac{∂F}{ ∂y} \\[4pt] \nonumber \dfrac{∂F}{ ∂φ} &= ρ \cos φ \cos θ \dfrac{∂F}{ ∂x} + ρ \cos φ \sin θ \dfrac{∂F}{ ∂y} − ρ \sin φ \dfrac{∂F}{ ∂z} \\[4pt] \end{align}\)}\]
Paso 4: Usa las tres fórmulas del Paso 3 para resolver para\(\dfrac{∂F}{ ∂x} , \dfrac{∂F}{ ∂y} , \dfrac{∂F}{ ∂z}\) en términos de\(\dfrac{∂F}{ ∂ρ} , \dfrac{∂F}{ ∂θ} , \dfrac{∂F}{ ∂φ} \).
Nuevamente, esto implica resolver un sistema de tres ecuaciones en tres incógnitas. Usando un proceso de eliminación similar al del Paso 2, obtenemos:
\[\fbox{\(\nonumber \begin{align}\dfrac{∂F}{ ∂x} &= \dfrac{1}{ ρ \sin φ} \left ( ρ \sin^2 φ \cos θ \dfrac{∂F}{ ∂ρ} − \sin θ \dfrac{∂F}{ ∂θ} + \sin φ \cos φ \cos θ \dfrac{∂F}{ ∂φ}\right ) \\[4pt] \nonumber \dfrac{∂F}{ ∂y} &= \dfrac{1}{ ρ \sin φ} \left ( ρ \sin^2 φ \sin θ \dfrac{∂F}{ ∂ρ} + \cos θ \dfrac{∂F}{ ∂θ} + \sin φ \cos φ \sin θ \dfrac{∂F}{ ∂φ}\right ) \\[4pt] \nonumber \dfrac{∂F}{ ∂z} &= \dfrac{1}{ρ} \left ( ρ \cos φ \dfrac{∂F}{ ∂ρ} − \sin φ \dfrac{∂F}{ ∂φ}\right ) \\[4pt] \end{align}\)}\]
Paso 5: Sustituir las fórmulas para i, j, k del Paso 2 y las fórmulas para\(\dfrac{∂F}{ ∂x} , \dfrac{∂F}{ ∂y} , \dfrac{∂F}{ ∂z}\) del Paso 4 en la fórmula de gradiente cartesiano\(∇F(x, y, z) = \dfrac{∂F}{ ∂x} \textbf{i}+ \dfrac{∂F}{ ∂y} \textbf{j}+ \dfrac{∂F}{ ∂z} \textbf{k}\).
Hacer este último paso es quizás el más tedioso, ¡ya que implica simplificar\(3×3+3×3+ 2×2 = 22\) términos! A saber,
\[\nonumber \begin{align} ∇F &= \dfrac{1}{ ρ \sin φ} \left ( ρ \sin^2 φ \cos θ \dfrac{∂F}{ ∂ρ} −\sin θ \dfrac{∂F}{ ∂θ} +\sin φ \cos φ \cos θ \dfrac{∂F}{ ∂φ}\right ) (\sin φ \cos θ \textbf{e}_ρ −\sin θ \textbf{e}_θ +\cos φ \cos θ \textbf{e}_φ) \\[4pt] \nonumber &+\dfrac{1}{ ρ \sin φ} \left ( ρ \sin^2 φ \sin θ \dfrac{∂F}{ ∂ρ} +\cos θ \dfrac{∂F}{ ∂θ} +\sin φ \cos φ \sin θ \dfrac{∂F}{ ∂φ}\right ) (\sin φ \sin θ \textbf{e}_ρ +\cos θ \textbf{e}_θ +\cos φ \sin θ \textbf{e}_φ)\\[4pt] \nonumber &+\dfrac{1}{ ρ} \left ( ρ \cos φ \dfrac{∂F}{ ∂ρ} −\sin φ \dfrac{∂F}{ ∂φ}\right ) (\cos φ \textbf{e}_ρ −\sin φ \textbf{e}_φ) ,\\[4pt] \end{align}\]
que vemos tiene 8 términos que involucran\(\textbf{e}_ρ\), 6 términos que involucran\(\textbf{e}_θ\) y 8 términos que involucran\(\textbf{e}_φ\). Pero el álgebra es sencillo y produce el resultado deseado:
\[∇F = \dfrac{∂F}{ ∂ρ} \textbf{e}_ρ + \dfrac{1}{ ρ \sin φ} \dfrac{∂F}{ ∂θ} \textbf{e}_θ + \dfrac{1}{ ρ} \dfrac{∂F}{ ∂φ} \textbf{e}_φ \quad \checkmark \]
Ejemplo 4.19
En el Ejemplo 4.17 mostramos eso\(∇\lVert \textbf{r} \rVert ^2 = 2\textbf{r} \text{ and }∆\lVert \textbf{r} \rVert ^2 = 6, \text{ where }\textbf{r}(x, y, z) = x\textbf{i} + y\textbf{j} + z\textbf{k}\) en coordenadas cartesianas. Verificar que obtengamos las mismas respuestas si cambiamos a coordenadas esféricas.
Solución
Desde\(\lVert \textbf{r} \rVert ^2 = x^ 2 + y^ 2 + z^ 2 = ρ^ 2 \text{ in spherical coordinates, let }F(ρ,θ,φ) = ρ^ 2 \) (para que\(F(ρ,θ,φ) = \lVert \textbf{r} \rVert ^2\)). El gradiente de\(F\) en coordenadas esféricas es
\[\nonumber \begin{align} ∇F &= \dfrac{∂F}{ ∂ρ} \textbf{e}_ρ + \dfrac{1}{ ρ \sin φ} \dfrac{∂F}{ ∂θ} \textbf{e}_θ + \dfrac{1}{ ρ} \dfrac{∂F}{ ∂φ} \textbf{e}_φ \\[4pt] \nonumber &=2ρ \textbf{e}_ρ + \dfrac{1}{ ρ \sin φ} (0)\textbf{e}_θ + \dfrac{1}{ ρ} (0)\textbf{e}_φ \\[4pt] \nonumber &= 2ρ \textbf{e}_ρ = 2ρ \dfrac{\textbf{r}}{ \lVert \textbf{r} \rVert} , \text{ as we showed earlier, so}\\[4pt] \nonumber &= 2ρ \dfrac{\textbf{r}}{ ρ} = 2\textbf{r} , \text{ as expected. And the Laplacian is} \\[4pt] \nonumber ∆F &= \dfrac{1}{ ρ^ 2} \dfrac{∂}{ ∂ρ} \left ( ρ^2 \dfrac{∂F}{ ∂ρ} \right ) + \dfrac{1}{ ρ^ 2 \sin^2 φ} \dfrac{∂^2F}{ ∂θ^2} + \dfrac{1}{ ρ^ 2 \sin φ} \dfrac{∂}{ ∂φ} \left ( \sin φ \dfrac{∂F}{ ∂φ}\right ) \\[4pt] \nonumber &= \dfrac{1}{ ρ^ 2} \dfrac{∂}{ ∂ρ} (ρ^ 2 2ρ) + \dfrac{1}{ ρ^ 2 \sin φ} (0) + \dfrac{1}{ ρ^ 2 \sin φ} \dfrac{∂}{ ∂φ} \left ( \sin φ(0)\right ) \\[4pt] \nonumber &= \dfrac{1}{ ρ^ 2} \dfrac{∂}{ ∂ρ} (2ρ^ 3 ) + 0 + 0 \\[4pt] \nonumber &= \dfrac{1}{ ρ^ 2} (6ρ^ 2 ) = 6 , \text{ as expected.} \\[4pt] \end{align}\]


