1.4: Funciones continuas

Como\((1.2 .8)\) indica, nos gustaría definir la tasa de cambio de una función\(y=f(x)\) con respecto a\(x\) como la sombra de la relación de dos cantidades,\(d y=\)\(f(x+d x)-f(x)\) y\(d x,\) siendo esta última un infinitesimal distinto de cero. De la discusión de la sección anterior, se deduce que podemos hacer esto si y sólo si el numerador\(d y\) es también un infinitesimal.

Definición

Decimos que una función\(f\) es continua en un número real\(c\) si por cada infinitesimal\(\epsilon\),

\[f(c+\epsilon) \simeq f(c)\]

Tenga en cuenta que\(f(c+\epsilon) \simeq f(c)\) es equivalente a\(f(c+\epsilon)-f(c) \simeq 0,\) eso es,\(f(c+\epsilon)-f(c)\) es un infinitesimal. En otras palabras, una función\(f\) es continua en un número real\(c\) si un cambio infinitesimal en el valor de\(c\) da como resultado un cambio infinitesimal en el valor de\(f\).

Ejemplo\(\PageIndex{1}\)

Si\(f(x)=x^{2},\) entonces, por ejemplo, para cualquier infinitesimal\(\epsilon\),

\[f(3+\epsilon)=(3+\epsilon)^{2}=9+6 \epsilon+\epsilon^{2} \simeq 9=f(3) .\]

De ahí\(f\) que sea continuo en\(x=3 .\) Más general, para cualquier número real\(x\),

\[f(x+\epsilon)=(x+\epsilon)^{2}=x^{2}+2 x \epsilon+\epsilon^{2} \simeq x^{2}=f(x) ,\]

de lo que se deduce que\(f\) es continuo en cada número real\(x .\)

Ejercicio\(\PageIndex{1}\)

Verificar que\(f(x)=3 x+4\) sea continuo en\(x=5\).

Ejercicio\(\PageIndex{2}\)

Verificar que\(g(t)=t^{3}\) sea continuo en\(t=2\).

Solución

Dados números reales\(a\) y\(b,\) dejamos

\[(a, b)=\{x | x \text { is a real number and } a<x<b\} ,\]

\[(a, \infty)=\{x | x \text { is a real number and } x>a\} ,\]

\[(-\infty, b)=\{x | x \text { is a real number and } x<b\} ,\]

y

\[(-\infty, \infty)=\mathbb{R} .\]

Un intervalo abierto es cualquier conjunto de una de estas formas.

Definición

Decimos que una función\(f\) es continua en un intervalo abierto\(I\) si\(f\) es continua en cada número real en\(I\).

Ejemplo\(\PageIndex{2}\)

De nuestro ejemplo anterior, se deduce que\(f(x)=x^{2}\) es continuo\((-\infty, \infty)\).

Ejercicio\(\PageIndex{3}\)

Verificar que\(f(x)=3 x+4\) sea continuo encendido\((-\infty, \infty)\).

Ejercicio\(\PageIndex{4}\)

Verificar que\(g(t)=t^{3}\) sea continuo encendido\((-\infty, \infty)\).

Ejercicio\(\PageIndex{3}\)

Llamamos a la función

\ [ H (t) =\ left\ {\ begin {array} {ll} {0,} & {\ text {if} t<0,}\\ {1,} & {\ text {if} t\ geq 0,}\ end {array}\ right. \] la función Heaviside (ver Figura 1.4.1). Si\(\epsilon\) es un infinitesimal positivo, entonces \ [ H (0+\ épsilon) =H (\ épsilon) =1=H (0), \] mientras que \ [ H (0-\ épsilon) =H (-\ épsilon) =0. \] Ya que 0 no es infinitesimalmente cercano a\(1,\) él se deduce que no\(H\) es continuo en\(0 .\) Sin embargo, para cualquier número real positivo\(a\) y cualquier infinitesimal\(\epsilon\) (positivo o negativo), \ [ H (a+\ épsilon) =1=H (a), \] desde\(a+\epsilon>0,\) y para cualquier número real negativo\(a\) y cualquier infinitesimal\(\epsilon\), \ [ H (a+\ épsilon) =0=H (a), \] ya que\(a+\epsilon<0 .\) Así\(H\) es continuo en ambos\((0, \infty)\) y\((-\infty, 0)\).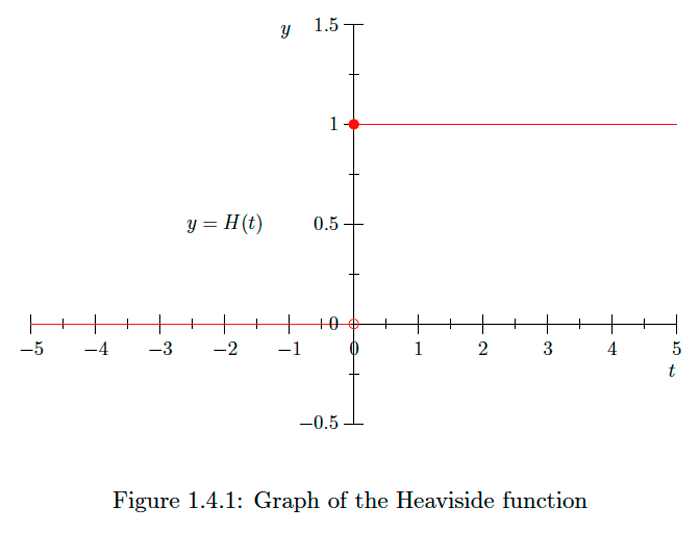

Tenga en cuenta que, en el ejemplo anterior, la función Heaviside satisface la condición de continuidad en 0 para infinitesimales positivos pero no para infinitesimales negativos. La siguiente definición aborda esta situación.

Definición

Decimos que una función\(f\) es continua desde la derecha en un número real\(c\) si por cada infinitesimal\(\epsilon>0\),

\ [ f (c+\ épsilon)\ simeq f (c). \] Del mismo modo, decimos que una función\(f\) es continua desde la izquierda en un número real\(c\) si por cada infinitesimal\(\epsilon>0\), \ [ f (c-\ épsilon)\ simeq f (c). \]

Ejemplo\(\PageIndex{4}\)

En el ejemplo anterior,\(H\) es continuo desde la derecha en\(t=0,\) pero no desde la izquierda.

Por supuesto, si\(f\) es continuo tanto desde la izquierda como desde la derecha en\(c,\) entonces\(f\) es continuo en\(c .\)

Ejemplo\(\PageIndex{5}\)

Supongamos

\ [ f (x) =\ left\ {\ begin {array} {ll} {3 x+5,} & {\ text {if} x\ leq 1,}\\ {10-2 x,} & {\ text {si} x>1.} \ end {array}\ right. \] Si\(\epsilon\) es un infinitesimal positivo, entonces \ [ f (1+\ épsilon) =3 (1+\ épsilon) +5=8+3\ épsilon\ simeq 8=f (1), \] así\(f\) es continuo desde la derecha en\(x=1,\) y \ [ f (1-\ épsilon) =3 (1-\ épsilon) +5=8-3\ épsilon\ simeq 8=f (1), \] así\(f\) es continuo de la izquierda en\(x=1\) también. De ahí\(f\) que sea continuo en\(x=1\).

Ejercicio\(\PageIndex{5}\)

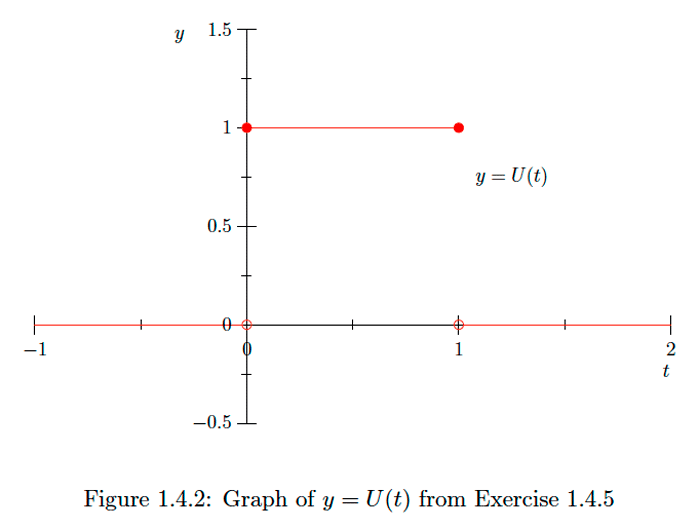
Verificar que la función

\ [ U (t) =\ left\ {\ begin {array} {ll} {0,} & {\ text {if} t1<0,}\\ {1,} & {\ text {if} 0\ leq t\ leq 1,}\\ {0,} & {\ text {if} t>,}\ end {array}\ right. \] es continuo desde la derecha en\(t=0\) y continuo desde la izquierda en\(t=1,\) pero no continuo en ninguno\(t=0\) o\(t=1 .\) Ver Figura\(1.4 .2 .\) Dado números reales\(a\) y\(b,\) dejamos \ [ [a, b] =\ {x | x\ text {es un número real y} a\ leq x\ leq b\}, \] \ [ [a,\ infty) =\ {x | x\ text {es un número real y} x\ geq a\}, \] y \ [ (-\ infty, b] =\ {x | x\ text {es un número real y} x\ leq b\}. \] Un intervalo cerrado es cualquier conjunto de una de estas formas.

Definición

Si\(a\) y\(b\) son números reales, decimos que una función\(f\) es continua en el intervalo cerrado\([a, b]\) si\(f\) es continua en el intervalo abierto\((a, b),\) continua desde la derecha en\(a\), y continua desde la izquierda en\(b\). Decimos\(f\) es continuo en el intervalo cerrado\([a, \infty)\) si\(f\) es continuo en el intervalo abierto\((a, \infty)\) y continuo desde la derecha en\(a .\) Decimos\(f\) es continuo en el intervalo cerrado\((-\infty, b]\) si\(f\) es continuo encendido\((-\infty, b)\) y continuo desde la izquierda en\(b\).

Ejemplo\(\PageIndex{6}\)

Podemos resumir nuestros resultados sobre la función Heaviside como\(H\) es continua una\((-\infty, 0)\) y otra vez\([0, \infty)\).

Ejercicio\(\PageIndex{6}\)

Explicar por qué la función\(U\) en el ejercicio anterior es continua en los intervalos\((-\infty, 0),[0,1],\) y\((1, \infty),\) pero no en el intervalo\((-\infty, \infty) .\)