1.5: Propiedades de las funciones continuas
- Page ID
- 117172
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Supongamos que\(f\) es continuo en el número real\(c\) y\(k\) es cualquier número real fijo. Si dejamos\(h(x)=k g(x),\) entonces, para cualquier infinitesimal\(\epsilon\),
\[h(c+\epsilon)-h(c)=k f(c+\epsilon)-k f(c)=k(f(c+\epsilon)-f(c))\] es un infinitesimal ya que, por suposición,\(f(c+\epsilon)-f(c)\) es un infinitesimal. De ahí\(h(c+\epsilon) \simeq h(c)\).Teorema\(\PageIndex{1}\)
Si\(f\) es continuo en\(c\) y\(k\) es cualquier número real fijo, entonces la función también\(h(x)=k f(x)\) es continua en\(c .\)
Ejemplo\(\PageIndex{1}\)
Hemos visto que\(f(x)=x^{2}\) es continuo en Ahora\((-\infty, \infty) .\) se deduce que, por ejemplo, también\(g(x)=5 x^{2}\) es continuo en\((-\infty, \infty)\).
Supongamos que ambos\(f\) y\(g\) son continuos en el número real\(c\) y dejamos que\(s(x)=f(x)+g(x) .\) si\(\epsilon\) es cualquier infinitesimal, entonces \[s(c+\epsilon)=f(c+\epsilon)+g(c+\epsilon) \simeq f(c)+g(c)=s(c) ,\] y así también\(s\) es continuo en\(c .\)Teorema\(\PageIndex{2}\)
Si\(f\) y\(g\) son ambos continuos en\(c,\) entonces la función
\[s(x)=f(x)+g(x)\] también es continuo en\(c .\)Ejemplo\(\PageIndex{2}\)
Desde
\[(x+\epsilon)^{3}=x^{3}+3 x^{2} \epsilon+3 x \epsilon^{2}+\epsilon^{3} \simeq x^{3}\] para cualquier número real\(x\) y cualquier infinitesimal\(\epsilon,\) se deduce que\(g(x)=x^{3}\) es continuo en\((-\infty, \infty) .\) De los teoremas anteriores, entonces sigue que \[h(x)=5 x^{2}+3 x^{3}\] es continuo en\((-\infty, \infty)\). Nuevamente, supongamos\(f\) y\(g\) son ambos continuos en\(c\) y dejar\(p(x)=f(x) g(x)\). Entonces, para cualquier infinitesimal\(\epsilon\), \[\begin{aligned} p(c+\epsilon)-s(c) &=f(c+\epsilon) g(c+\epsilon)-f(c) g(c) \\[12pt] &=f(c+\epsilon) g(c+\epsilon)-f(c) g(c+\epsilon)+f(c) g(c+\epsilon)-f(c) g(c) \\[12pt] &=g(c+\epsilon)(f(c+\epsilon)-f(c))+f(c)(g(c+\epsilon)-g(c)), \end{aligned}\] que es infinitesimal ya que ambos\(f(c+\epsilon)-f(c)\) y\(g(c+\epsilon)-g(c)\) son. Por lo tanto\(p\) es continuo en\(c .\)Teorema\(\PageIndex{3}\)
Si\(f\) y\(g\) son ambos continuos en\(c,\) entonces la función
\[p(x)=f(x) g(x)\] también es continuo en\(c .\) Finalmente, supongamos\(f\) y\(g\) son continuos en\(c\) y\(g(c) \neq 0 .\) Let\(q(x)=\frac{f(x)}{g(x)}\). Entonces, para cualquier infinitesimal\(\epsilon,\) \[\begin{aligned} q(c+\epsilon)-q(c) &=\frac{f(c+\epsilon)}{g(c+\epsilon)}-\frac{f(c)}{g(c)} \\[12pt] &=\frac{f(c+\epsilon) g(c)-f(c) g(c+\epsilon)}{g(c+\epsilon) g(c)} \\[12pt] &=\frac{f(c+\epsilon) g(c)-f(c) g(c)+f(c) g(c)-f(c) g(c+\epsilon)}{g(c+\epsilon) g(c)} \\[12pt] &=\frac{g(c)(f(c+\epsilon)-f(c))-f(c)(g(c+\epsilon)-g(c))}{g(c+\epsilon) g(c)}, \end{aligned}\] que sea infinitesimal ya que ambos\(f(c+\epsilon)-f(c)\) y\(g(c+\epsilon)-g(c)\) son infinitesimales, y no\(g(c) g(c+\epsilon)\) es un infinitesimal. Por lo tanto\(q\) es continuo en\(c .\)Teorema\(\PageIndex{4}\)
Si\(f\) y\(g\) son ambos continuos en\(c\) y\(g(c) \neq 0,\) luego la función
\[q(x)=\frac{f(x)}{g(x)}\] es continuo en\(c .\)Ejercicio\(\PageIndex{1}\)
Explicar por qué
\[f(x)=\frac{3 x+4}{x^{2}+1}\] es continuo en\((-\infty, \infty)\).Polinomios y funciones racionales
Ahora es posible identificar dos clases importantes de funciones continuas. Primero, toda función constante es continua: en efecto, si\(f(x)=k\) para todos los valores reales\(x,\) y\(k\) es cualquier constante real, entonces para cualquier infinitesimal\(\epsilon\),
\[f(x+\epsilon)=k=f(x) .\] A continuación, la función\(f(x)=x\) es continua para todos los reales\(x\) ya que, para cualquier infinitesimal\(\epsilon\), \[f(x+\epsilon)=x+\epsilon \simeq x=f(x) .\] Dado que el producto de las funciones continuas es continuo, ahora se deduce que, para cualquier entero no negativo\(n, g(x)=x^{n}\) es continuo en\((-\infty, \infty)\) ya que es un función constante si\(n=0\) y un producto de\(f(x)=x\) por sí mismo\(n\) veces lo contrario. De esto se deduce (ya que los múltiplos constantes de funciones continuas vuelven a ser continuos) que todos los monomios, es decir, funciones de la forma\(f(x)=a x^{n},\) donde\(a\) es una constante real fija y\(n\) es un entero no negativo, son continuas. Ahora un polinomio es una función de la forma \[P(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} ,\] donde\(a_{0}, a_{1}, \ldots, a_{n}\) son constantes reales y\(n\) es un entero no negativo. Es decir, un polinomio es una suma de monomios. Dado que las sumas de funciones continuas son continuas, ahora tenemos el siguiente resultado fundamental.Teorema\(\PageIndex{5}\)
Si\(P\) es un polinomio, entonces\(P\) es continuo en\((\infty, \infty)\).
Ejemplo\(\PageIndex{3}\)
La función
\[f(x)=32+14 x^{5}-6 x^{7}+\pi x^{14}\] es continuo en\((-\infty, \infty)\). Una función racional es una relación de polinomios. Es decir, si\(P(x)\) y\(Q(x)\) son polinomios, entonces \[R(x)=\frac{P(x)}{Q(x)}\] es una función racional. ya que las proporciones de funciones continuas son continuas, tenemos lo siguiente.Teorema\(\PageIndex{6}\)
Si\(R\) es función racional, entonces\(R\) es continua en cada punto de su dominio.
Ejemplo\(\PageIndex{4}\)
Si
\[f(x)=\frac{3 x-4}{x^{2}-1} ,\] entonces\(f\) es una función racional definida para todos los reales\(x\) excepto\(x=-1\) y\(x=1 .\) Así\(f\) es continua en los intervalos\((-\infty,-1),(-1,1),\) y\((1, \infty) .\)Ejercicio\(\PageIndex{2}\)
Encuentra los intervalos en los que
\[f(x)=\frac{3 x^{2}-1}{x^{3}+1}\] es continuo.- Contestar
-
\((-\infty,-1)\)y\((-1, \infty)\)
Funciones trigonométricas
Recordemos que si\(t\) es un número real y\((a, b)\) es el punto en el plano que se encuentra atravesando el círculo unitario a\(x^{2}+y^{2}=1\) una distancia de\((1,0),\) en sentido contrario\(|t|\) a las agujas del reloj si\(t \geq 0\) y en el sentido de las agujas del reloj de lo contrario, entonces
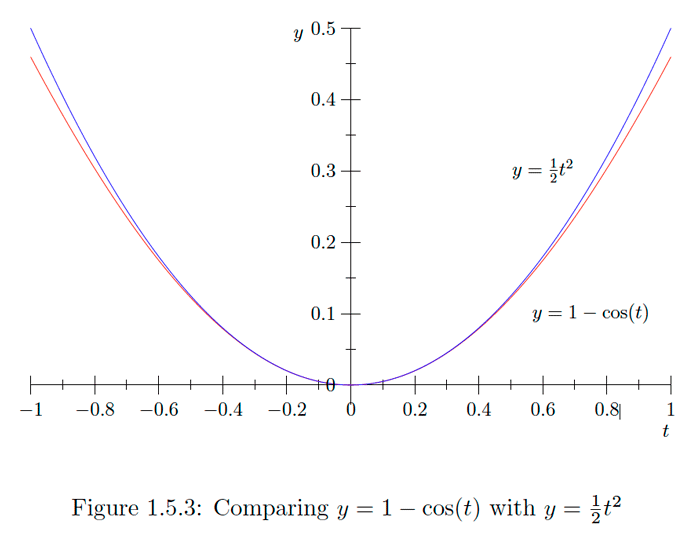
\[a=\cos (t)\] \[b=\sin (t) .\] Tenga en cuenta que para\(0<t<\pi\), como en la Figura\(1.5 .1, t\) es mayor que la longitud del segmento de línea de\(A=(1,0)\) a\(B=(\cos (t), \sin (t)) .\) Ahora el segmento de\(A\) a\(B\) es la hipotenusa del triángulo rectángulo con vértices en\(A, B,\)\(C=(\cos (t), 0) . \text { since the distance from } C \text { to } A \text { is } 1-\cos (t))\) y y distancia de\(B\) a\(C\) es se\(\sin (t),\) deduce del teorema de Pitágoras que \[\begin{aligned} t^{2} &>(1-\cos (t))^{2}+\sin ^{2}(t) \\ &=1-2 \cos (t)+\cos ^{2}(t)+\sin ^{2}(t) \\ &=2-2 \cos (t) . \end{aligned}\] Un diagrama similar revela el mismo resultado para\(-\pi<t<0 .\) Por otra parte, ambos\(t^{2}\) y\(2-2 \cos (t)\) son 0 cuando\(t=0,\) así lo tenemos\(t^{2} \geq 2-2 \cos (t)\) para todos\(-\pi<t<\pi\). Adicionalmente,\(0 \leq 2-2 \cos (t) \leq 4 \text { for all } t \text { (since }-1 \leq \cos (t) \leq 1 \text { for all } t)\), así que ciertamente\(t^{2}>2-2 \cos (t)\) siempre\(|t|>2 .\) De ahí que hayamos demostrado que \[0 \leq 2-2 \cos (t) \leq t^{2}\]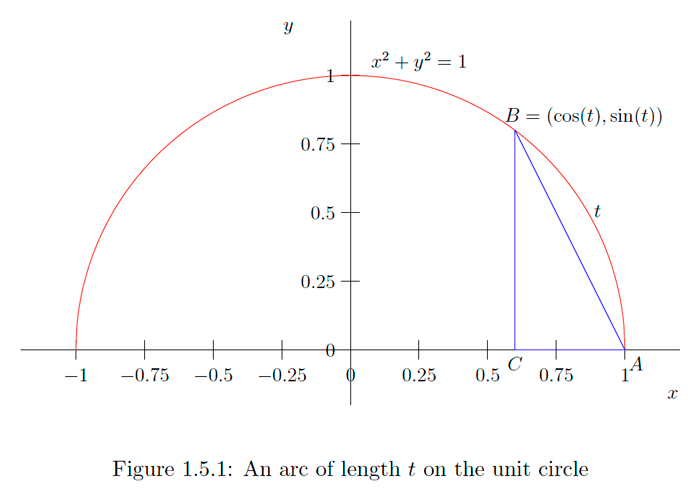
\[1-\frac{t^{2}}{2} \leq \cos (t) \leq 1\]
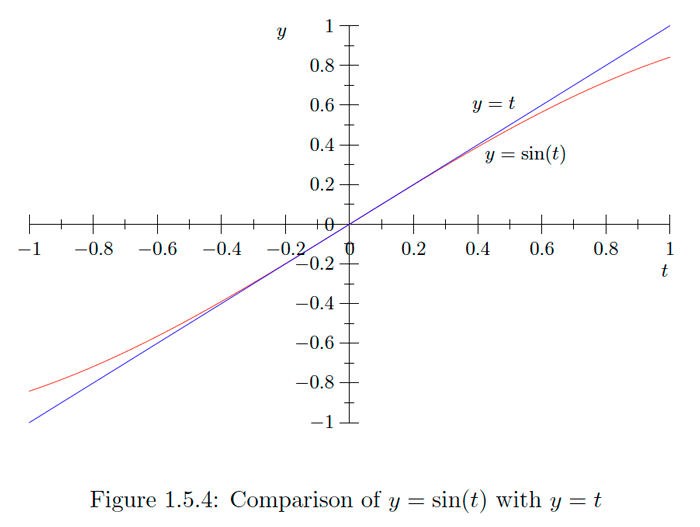
para todos\(t .\) En particular, si\(\epsilon\) es un infinitesimal, entonces \[1-\frac{\epsilon^{2}}{2} \leq \cos (\epsilon) \leq 1\] implica \[\cos (0+\epsilon)=\cos (\epsilon) \simeq 1=\cos (0) .\] que es decir, la función\(f(t)=\cos (t)\) es continua en\(t=0 .\) Por otra parte, ya que\(0 \leq 1+\cos (t) \leq 2\) para todos\(t\), \[\begin{aligned} \sin ^{2}(t) &=1-\cos ^{2}(t) \\ &=(1-\cos (t))(1+\cos (t)) \\ & \leq \frac{t^{2}}{2}(1+\cos (t)) \\ & \leq t^{2} , \end{aligned}\] de lo que se deduce que \[|\sin (t)| \leq|t|\] para cualquier valor de\(t .\) En particular, para cualquier infinitesimal\(\epsilon\), \[|\sin (0+\epsilon)|=|\sin (\epsilon)| \leq \epsilon ,\] de lo que se deduce \[\sin (\epsilon) \simeq 0=\sin (0) .\] que Es decir, la función\(g(t)=\sin (t)\) es continua en\(t=0\). Usando las fórmulas de suma de ángulo para seno y coseno, vemos que, para cualquier número real\(t\) e infinitesimal\(\epsilon\), \[\cos (t+\epsilon)=\cos (t) \cos (\epsilon)-\sin (t) \sin (\epsilon) \simeq \cos (t)\] y \[\sin (t+\epsilon)=\sin (t) \cos (\epsilon)+\cos (t) \sin (\epsilon) \simeq \sin (t) ,\] desde\(\cos (\epsilon) \simeq 1\) y\(\sin (\epsilon)\) es un infinitesimal. De ahí que tengamos el siguiente resultado.Teorema\(\PageIndex{7}\)
Las funciones\(f(t)=\cos (t)\) y\(g(t)=\sin (t)\) son continuas en\((-\infty, \infty)\).
El siguiente teorema se desprende ahora de nuestros resultados anteriores sobre las funciones continuas.
Teorema\(\PageIndex{8}\)
Las siguientes funciones son continuas en cada punto en sus respectivos dominios:
\[\tan (t)=\frac{\sin (t)}{\cos (t)} ,\] \[\cot (t)=\frac{\cos (t)}{\sin (t)} ,\] \[\sec (t)=\frac{1}{\cos (t)} ,\] \[\csc (t)=\frac{1}{\sin (t)} ,\] Con un poco más de geometría, podemos mejorar las desigualdades en\((1.5 .13)\) y\((1.5 .18) .\) Considerar un ángulo\(0<t<\frac{\pi}{2},\) let\(A=(1,0)\) y\(B=(\cos (t), \sin (t))\) como arriba, y dejar que\(D\) sea el punto de intersección de las líneas tangentes a el círculo\(\left.x^{2}+y^{2}=1 \text { at } A \text { and } B \text { (see Figure } 1.5 .2\right) .\) Tenga en cuenta que el triángulo con vértices en\(A, B,\) y\(D\) es isósceles con base de longitud\(\sqrt{2(1-\cos (t))}\) (como se deriva anteriormente) y ángulos base\(\frac{t}{2} .\) Además, la suma de las longitudes de las dos patas excede\(t\). ya que cada pata es de longitud \[\frac{\frac{1}{2} \sqrt{2(1-\cos (t))}}{\cos \left(\frac{t}{2}\right)} ,\]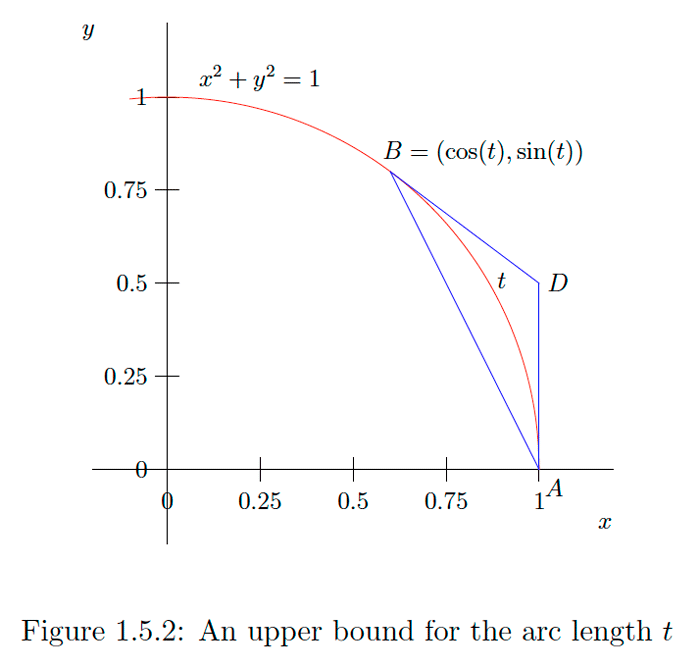
Ejemplo\(\PageIndex{5}\)
Para una comparación numérica, tenga en cuenta que para\(t=0.1, \cos (t)= 0.9950042,\) comparado\(1-\frac{t^{2}}{2}=0.995,\) y\(\sin (t)=0.0998334,\) comparado con\(t=0.1\)
Ejercicio\(\PageIndex{3}\)
Verificar que el triángulo con vértices en\(A, B,\) y\(D\) en la Figura 1.5 .2 sea un triángulo isósceles con ángulos base de\(\frac{t}{2}\) at\(A\) y\(B\).
Ejercicio\(\PageIndex{4}\)
Verificar la fórmula de medio ángulo,
\[\cos (\theta)=\frac{1}{2}(1+\cos (2 \theta)) ,\] para cualquier ángulo\(\theta,\) usando las identidades\(\cos (2 \theta)=\cos ^{2}(\theta)-\sin ^{2}(\theta)\) (una consecuencia de la fórmula de adición) y\(\sin ^{2}(\theta)+\cos ^{2}(\theta)=1\).Composiciones
Dadas funciones\(f\) y\(g,\) llamamos a la función
\[f \circ g(x)=f(g(x))\] la composición de\(f\) con\(g .\) Si\(g\) es continua en un número real\(c, f\) es continua en\(g(c),\) y\(\epsilon\) es un infinitesimal, entonces \[f \circ g(c+\epsilon)=f(g(c+\epsilon)) \simeq f(g(c))\] desde\(g(c+\epsilon) \simeq g(c)\).Teorema\(\PageIndex{9}\)
Si\(g\) es continuo en\(c\) y\(f\) es continuo en\(g(c),\) entonces\(f \circ g\) es continuo en\(c .\)
Ejemplo\(\PageIndex{6}\)
Dado que\(f(t)=\sin (t)\) es continuo para todos\(t\) y
\[g(t)=\frac{3 t^{2}+1}{4 t-8}\] es continuo en todos los números reales excepto\(t=2,\) se deduce que \[h(t)=\sin \left(\frac{3 t^{2}+1}{4 t-8}\right)\] es continuo en los intervalos\((-\infty, 2)\) y\((2, \infty)\). Tenga en cuenta que si\(f(x)=\sqrt{x}\) y\(\epsilon\) es un infinitesimal, entonces, para cualquiera\(x \neq 0\), \[\begin{aligned} f(x+\epsilon)-f(x) &=\sqrt{x+\epsilon}-\sqrt{x} \\ &=(\sqrt{x+\epsilon}-\sqrt{x})\left(\frac{\sqrt{x+\epsilon}+\sqrt{x}}{\sqrt{x+\epsilon}+\sqrt{x}}\right) \\ &=\frac{x+\epsilon-x}{\sqrt{x+\epsilon}+\sqrt{x}} \\ &=\frac{\epsilon}{\sqrt{x+\epsilon}+\sqrt{x}} , \end{aligned}\] que es infinitesimal. De ahí\(f\) es continuo en\((0, \infty) .\) Por otra parte, si\(\epsilon\) es un infinitesimal positivo, entonces\(\sqrt{\epsilon}\) debe ser un infinitesimal (ya que si no\(a=\sqrt{\epsilon}\) es un infinitesimal, entonces no\(a^{2}=\epsilon\) es un infinitesimal). Por \[f(0+\epsilon)=\sqrt{\epsilon} \simeq 0=f(0) .\] lo tanto,\(f\) es continuo en\(0,\) y así\(f(x)=\sqrt{x}\) es continuo en\([0, \infty)\).Teorema\(\PageIndex{10}\)
La función\(f(x)=\sqrt{x}\) es continua\([0, \infty)\).
Ejemplo\(\PageIndex{7}\)
Ahora se deduce que\(f(x)=\sqrt{4 x-2}\) es continuo en todas partes se define, es decir, en\([2, \infty)\).
Ejercicio\(\PageIndex{5}\)
Encuentra el intervalo o intervalos en los que\(f(x)=\sin \left(\frac{1}{x}\right)\) es continuo.
- Contestar
-
\((-\infty, 0)\)y\((0, \infty)\)
Ejercicio\(\PageIndex{6}\)
Encuentre el intervalo o intervalos en los que
\[g(t)=\sqrt{\frac{1+t^{2}}{1-t^{2}}}\] es continuo.- Contestar
-
\((-\infty,-1),(-1,1)\)y\((1, \infty)\)
Consecuencias de la continuidad
Las funciones continuas tienen dos propiedades importantes que jugarán un papel clave en nuestras discusiones en el resto del texto: la propiedad de valor extremo y la propiedad de valor intermedio. Ambas propiedades se basan en aspectos técnicos de los números reales que se encuentran más allá del alcance de este texto, por lo que no intentaremos justificaciones.
La propiedad de valor extremo establece que una función continua en un intervalo cerrado\([a, b]\) alcanza un valor máximo y mínimo.Teorema\(\PageIndex{11}\)
Si\(f\) es continuo en un intervalo cerrado\([a, b],\) entonces existe un número real\(c\) en\([a, b]\) para el cual\(f(c) \leq f(x)\) para todos\(x\) en\([a, b]\) y un número real\(d\) en\([a, b]\) para el cual\(f(d) \geq f(x)\) para todos\(x\) en\([a, b] .\)
Los siguientes ejemplos muestran la necesidad de las dos condiciones del teorema (es decir, la función debe ser continua y el intervalo debe ser cerrado para asegurar la conclusión).
Ejemplo\(\PageIndex{8}\)
La función no\(f(x)=x^{2}\) alcanza ni un valor máximo ni mínimo en el intervalo\((0,1)\). En efecto, dado cualquier punto\(a\) en\((0,1), f(x)>f(a)\) cuando\(a<x<1\) y\(f(x)<f(a)\) cuando Por\(0<x<a .\) supuesto, esto no contradice el teorema porque no\((0,1)\) es un intervalo cerrado. En el intervalo cerrado\([0,1],\) tenemos\(f(1) \geq f(x)\) para todos\(x\) en\([0,1]\) y\(f(0) \leq f(x)\) para todos\(x\) de acuerdo con el teorema.\([0,1],\)
En este ejemplo los valores extremos de\(f\) ocurrieron en los puntos finales del intervalo\([-1,1] .\) Esto no tiene por qué ser el caso. Por ejemplo, si\(g(t)=\sin (t),\) entonces, en el intervalo\([0,2 \pi], g\) tiene un valor mínimo de\(-1\) at\(t=\frac{3 \pi}{2}\) y un valor máximo de 1 at\(t=\frac{\pi}{2}\).
Ejemplo\(\PageIndex{9}\)
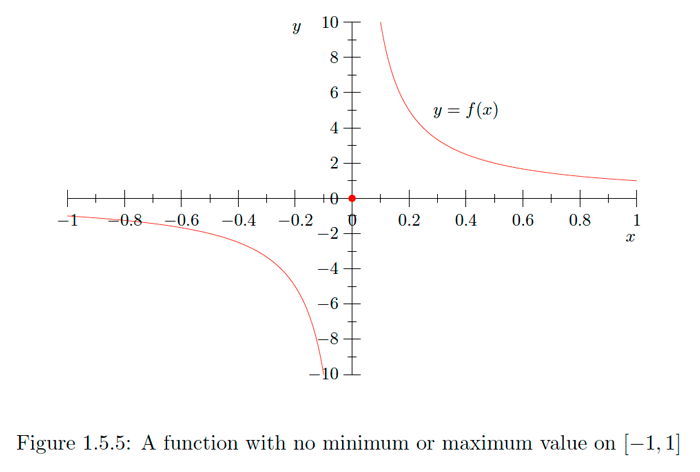
Let
\[f(x)=\left\{\begin{array}{ll}{\frac{1}{x},} & {\text { if }-1 \leq x<0 \text { or } 0<x \leq 1} , \\ {0,} & {\text { if } x=0.}\end{array}\right.\] Ver Figura\(1.5 .5 .\) Entonces\(f\) no tiene un valor máximo: si\(a \leq 0,\) entonces\(f(x)>f(a)\) para cualquiera\(x>0,\) y si\(a>0,\) entonces\(f(x)>f(a)\) cuando sea\(0<x<a\). Del mismo modo, no\(f\) tiene valor mínimo: si\(a \geq 0,\) entonces\(f(x)<f(a)\) para alguno\(x<0\), y si\(a<0,\) entonces\(f(x)<f(a)\) siempre que\(a<x<0 .\) El problema esta vez\(f\) es que no es continuo en\(x=0 .\) Efectivamente, si\(\epsilon\) es un infinitesimal, entonces\(f(\epsilon)\) es infinito, y, por lo tanto, no infinitesimalmente cercano a\(f(0)=0\).Ejercicio\(\PageIndex{7}\)
Encuentre un ejemplo de una función continua que tenga tanto un valor mínimo como un valor máximo en el intervalo abierto\((0,1)\).
Ejercicio\(\PageIndex{8}\)
Encuentre un ejemplo de función que tenga un valor mínimo y un valor máximo en el intervalo\([0,1],\) pero que no sea continua en\([0,1] .\)
La propiedad de valor intermedio establece que una función continua alcanza todos los valores entre dos valores dados cualquiera de la función.
Teorema\(\PageIndex{12}\)
Si\(f\) es continuo en el intervalo\([a, b]\) y\(m\) es cualquier valor entre\(f(a)\) y\(f(b),\) entonces existe un número real\(c\) en\([a, b]\) el que\(f(c)=m .\)
El siguiente ejemplo muestra que una función que no es continua no necesita satisfacer la propiedad de valor intermedio.
Ejemplo\(\PageIndex{10}\)
Si\(H\) es la función Heaviside, entonces\(H(-1)=0\) y\(H(1)= 1\), pero no existe ningún número real\(c\) en\([-1,1]\) el que\(H(c)=\frac{1}{2},\) aunque\(0<\frac{1}{2}<1 .\)


