2.7: Las funciones exponenciales y logaritmos
- Page ID
- 117230
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Existen muchas aplicaciones en las que es necesario encontrar una función\(y\) de una variable\(t\) que tenga la propiedad de que
\[\frac{d y}{d t}=k y\]
para algunos números reales constantes\(k .\) Los ejemplos incluyen modelar el crecimiento de ciertas poblaciones animales, donde\(y\) está el tamaño de la población en el momento\(t\) y\(k>0\) depende de la velocidad a la que la población está creciendo, y describir la desintegración de una sustancia radiactiva, donde \(y\)es la cantidad de un material radiactivo presente en el momento\(t\) y\(k<0\) depende de la velocidad a la que el elemento decae. Primero consideraremos\(k=1 ;\) ese caso es decir, buscaremos una función\(y=f(t)\) con la propiedad que\(f^{\prime}(t)=f(t)\).
2.7.1 La Función Exponencial
Supongamos que\(f\) es una función diferencial on\((-\infty, \infty)\) con la propiedad que\(f^{\prime}(t)=f(t)\) para todos\(t\) (uno puede demostrar que efectivamente existe tal función, aunque aquí no entraremos en los detalles). Ahora\(f^{\prime}(t)=f(t)\) implica, por el teorema fundamental del cálculo, que
\[\int_{0}^{t} f(x) d x=\int_{0}^{t} f^{\prime}(x) d x=f(t)-f(0)\]
para todos\(t .\) El valor de\(f(0 \text { is arbitrary; we will find it convenient to take } f(0)=1\). Es decir, ahora estamos buscando una función\(f\) que satisfaga
\[f(t)=1+\int_{0}^{t} f(x) d x .\]
Supongamos que\([0, t]\) dividimos en\(N\) subintervalos de igual longitud\(\Delta x=\frac{t}{N},\) donde\(N\) es un entero positivo, y dejar que\(x_{0}, x_{1}, x_{2}, \ldots, x_{N}\) sean los puntos finales de estos intervalos. Ahora para cualquier\(i=1,2, \ldots, N,\) uso\((2.7 .3),\)
\[\begin{aligned} f\left(x_{i}\right) &=1+\int_{0}^{x_{i}} f(x) d x \\ &=1+\int_{0}^{x_{i-1}} f(x) d x+\int_{x_{1-1}}^{x_{i}} f(x) d x \\ &=f\left(x_{i-1}\right)+\int_{x_{1-1}}^{x_{i}} f(x) d x .\end{aligned}\]
Además, para los pequeños\(\Delta x\),
\[\int_{x_{1-1}}^{x_{i}} f(x) d x \approx f\left(x_{i-1}\right) \Delta x,\]
y así tenemos
\[f\left(x_{i}\right) \approx f\left(x_{i-1}\right)+f\left(x_{i-1}\right) \Delta x=f\left(x_{i-1}\right)(1+\Delta x).\]
De ahí que tengamos
\[\begin{aligned} f\left(x_{0}\right) &=f(0)=1 \\ f\left(x_{1}\right) & \approx f\left(x_{0}\right)(1+\Delta x)=1+\Delta x \\ f\left(x_{2}\right) & \approx f\left(x_{1}\right)(1+\Delta x) \approx(1+\Delta x)^{2} \\ f\left(x_{3}\right) & \approx f\left(x_{2}\right)(1+\Delta x) \approx(1+\Delta x)^{3} \\ f\left(x_{4}\right) & \approx f\left(x_{3}\right)(1+\Delta x) \approx(1+\Delta x)^{4} \\ \vdots & \vdots \\ f\left(x_{N}\right) & \approx f\left(x_{N-1}\right)(1+\Delta x) \approx(1+\Delta x)^{N} \end{aligned}\]
Ahora\(x_{N}=t\) y\(\Delta x=\frac{t}{N},\) así tenemos
\[f(t) \approx\left(1+\frac{t}{N}\right)^{N}.\]
Además, si seguimos el mismo procedimiento con\(N\) infinito y\(d x=\frac{t}{N},\) deberíamos esperar (aunque no lo hemos probado)
\[f(t) \simeq\left(1+\frac{t}{N}\right)^{N}.\]
Vamos a dejar Es\(e=f(1) .\) decir,
\[e=\operatorname{sh}\left(1+\frac{1}{N}\right)^{N},\]
donde\(N\) es cualquier entero infinito positivo. Llamamos al número de\(e\) Euler. Ahora si\(t\) hay algún número real, entonces
\[f(t)=\left(1+\frac{t}{N}\right)^{N}=\left(\left(1+\frac{1}{\frac{N}{t}}\right)^{\frac{N}{t}}\right)^{t}=e^{t},\]
donde hemos utilizado el hecho de que\(\frac{N}{t}\) es infinito ya que\(N\) es infinito y\(t\) es finito. (Tenga en cuenta, sin embargo, que no\(\frac{N}{t}\) es un entero, como se requiere en\((2.7 .16) .\) La declaración es sin embargo cierto, pero este es un detalle que no vamos a perseguir aquí.) Así
la función
\[f(t)=e^{t}\]
tiene la propiedad\(f^{\prime}(t)=f(t),\) que es decir,
\[\frac{d}{d t} e^{t}=e^{t}.\]
De hecho, se puede demostrar que\(f(t)=e^{t}\) es la única función para la cual\(f(0)=1\) y\(f^{\prime}(t)=f(t) .\) Nosotros llamamos a esta función la función exponencial, y a veces escribimos\(\exp (t)\) para\(e^{t} .\)
Se ha demostrado que\(e\) es un número irracional. Aunque, como puede\(\pi,\) que no expresemos\(e\) exactamente en notación decimal, podemos usar\((2.7 .16)\) para encontrar aproximaciones, reemplazando el infinito\(N\) por un gran valor finito\(N .\) para Por ejemplo, con\(N=200,000,\) encontramos que
\[e \approx\left(1+\frac{1}{200000}\right)^{200000} \approx 2.71828,\]
que es correcto a 5 decimales.
Ejemplo\(\PageIndex{1}\)
Si\(f(t)=e^{5 t},\) entonces\(f\) es la composición de\(h(t)=5 t\) y\(g(u)=e^{u} .\) Por lo tanto, usando la regla de la cadena,
\[f^{\prime}(t)=g^{\prime}(h(t)) h^{\prime}(t)=e^{5 t} \cdot 5=5 e^{5 t}.\]En general, si\(h(t)\) es diferenciable, entonces, por la regla de la cadena,\[\frac{d}{d t} e^{h(t)}=h^{\prime}(t) e^{h(t)}.\]
Ejemplo\(\PageIndex{2}\)
Si\(f(x)=6 e^{-x^{2}},\) entonces
\[f^{\prime}(x)=-12 x e^{-x^{2}}.\]
Ejercicio\(\PageIndex{1}\)
Encuentra la derivada de\(g(x)=12 e^{-7 x}\).
- Contestar
-
\(g^{\prime}(x)=-84 e^{-7 x}\)
Ejercicio\(\PageIndex{2}\)
Encuentra la derivada de\(f(t)=3 t^{2} e^{-t}\).
- Contestar
-
\(f^{\prime}(t)=\left(6 t-3 t^{2}\right) e^{-t}\)
Ejemplo\(\PageIndex{3}\)
Vamos\(f(t)=e^{t}\) y\(g(t)=e^{-t} .\) ya que\(e^{t}>0\) por todo lo que\(t,\) tenemos\(f^{\prime}(t)=e^{t}>0\) y\(f^{\prime \prime}(t)=e^{t}>0\) para todos\(t,\) y así\(f\) va aumentando\((-\infty, \infty)\) y la gráfica de\(f\) es cóncava hacia arriba\((-\infty, \infty) .\) en Por otro lado,\(g^{\prime}(t)=-e^{-t}<0\) y\(g^{\prime \prime}(t)=e^{-t}>0\) para todos\(t,\) así \(g\)está disminuyendo\((-\infty, \infty)\) y la gráfica de\(g\) es cóncava hacia arriba en\((-\infty, \infty) .\) Ver Figura\(2.7 .1 .\)
Por supuesto, de\((2.7 .19)\) eso se desprende\[\int e^{t} d t=e^{t}+c.\]
Ejemplo\(\PageIndex{4}\)
Por lo que hemos visto con los ejemplos de derivados anteriores, tenemos
\[\int_{0}^{1} e^{-t} d t=-\left.e^{-t}\right|_{0} ^{1}=-e^{-1}+e^{0}=1-e^{-1} \approx 0.6321.\]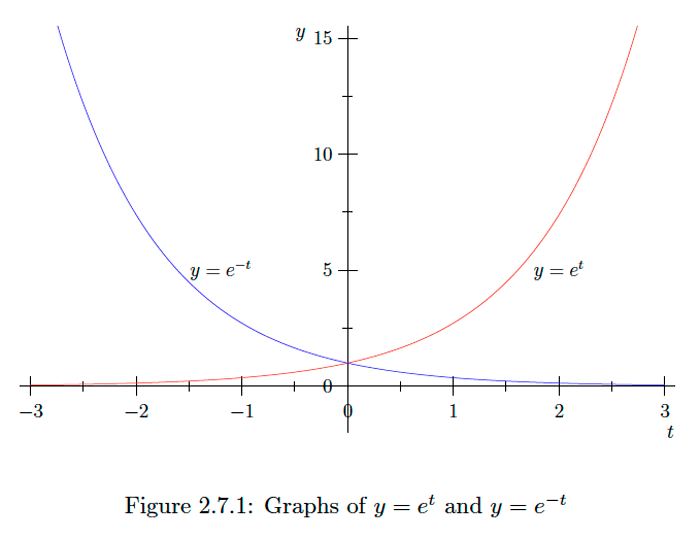
Ejemplo\(\PageIndex{5}\)
Evaluar
\[\int x e^{-x^{2}} d x,\]usaremos el cambio de la variable\[\begin{aligned} u &=-x^{2} \\ d u &=-2 x d x. \end{aligned}\] Entonces\[\int x e^{-^{2}} d x=-\frac{1}{2} \int e^{u} d u=-\frac{1}{2} e^{u}+c=-\frac{1}{2} e^{-x^{2}}+c.\]
Ejemplo\(\PageIndex{6}\)
Evaluar
\[\int x e^{-2 x} d x,\]usaremos integración por partes:\[\begin{aligned} u &=x & & d v=e^{-2 x} d x \\ d u &=d x & & v=-\frac{1}{2} e^{-2 x} .\end{aligned}\] Entonces\[\int x e^{-2 x} d x=-\frac{1}{2} x e^{-2 x}+\frac{1}{2} \int e^{-2 x} d x=-\frac{1}{2} x e^{-2 x}-\frac{1}{4} e^{-2 x}+c.\]
Ejercicio\(\PageIndex{3}\)
Evaluar\(\int_{0}^{4} 5 e^{-2 x} d x\).
- Contestar
-
\(\int_{0}^{4} 5 e^{-2 x} d x=\frac{5}{2}-\frac{5}{2} e^{-8} \approx 2.4992\)
Ejercicio\(\PageIndex{4}\)
Evaluar\(\int_{0}^{1} x^{2} e^{-x^{3}} d x\).
- Contestar
-
\(\int_{0}^{1} x^{2} e^{-x^{3}} d x=\frac{1}{3}(1-e) \approx 0.2107\)
Ejercicio\(\PageIndex{5}\)
Evaluar\(\int x^{2} e^{-x} d x\).
- Contestar
-
\(\int x^{2} e^{-x} d x=-2 e^{-x}-2 x e^{-x}-x^{2} e^{-x}+c\)
Tenga en cuenta que si\(y=a e^{k t},\) donde\(a\) y\(k\) hay alguna constante real, entonces
\[\frac{d y}{d t}=k a e^{k t}=k y.\]
Es decir,\(y\) satisface la ecuación diferencial\((2.7 .1)\) con la que iniciamos esta sección. Consideraremos ejemplos de aplicaciones de esta ecuación después de una discusión de la función logaritmo, la inversa de la función exponencial.
2.7.2 La función logaritmo
La función logaritmo es la inversa de la función exponencial. Es decir, para un número real positivo\(x, y=\log (x),\) leer\(y\) es el logaritmo de\(x,\) si y solo si\(e^{y}=x .\) En particular, tenga en cuenta que para cualquier número real positivo\(x,\)
\[e^{\log (x)}=x,\]
y para cualquier número real\(x\),
\[\log \left(e^{x}\right)=x.\]
También, ya que\(e^{0}=1,\) se deduce de eso\(\log (1)=0\).
Ya que\(\log (x)\) es el poder al que se debe elevar\(e\) para obtener\(x,\) logaritmos heredar sus propiedades básicas de las propiedades de los exponentes. Por ejemplo, para cualquier número real positivo\(x\) y\(y,\)
\[\log (x y)=\log (x)+\log (y)\]
desde
\[e^{\log (x)+\log (y)}=e^{\log (x)} e^{\log (y)}=x y.\]
Del mismo modo, para cualquier número real positivo\(x\) y cualquier número real\(a\),
\[\log \left(x^{a}\right)=a \log (x)\]
desde
\[e^{a \log (x)}=\left(e^{\log (x)}\right)^{a}=x^{a}.\]
Ejercicio\(\PageIndex{6}\)
Verificar que para cualquier número real positivo\(x\) y\(y\),
\[\log \left(\frac{x}{y}\right)=\log (x)-\log (y).\]Obsérvese en particular que esto implica que\[\log \left(\frac{1}{y}\right)=-\log (y).\] Para encontrar la derivada de la función logaritmo, primero observamos que si\(y=\log (x),\) entonces\(e^{y}=x,\) y así\[\frac{d}{d x} e^{y}=\frac{d}{d x} x.\] Aplicando la regla de la cadena, se deduce que\[e^{y} \frac{d y}{d x}=1.\] Por lo tanto\[\frac{d y}{d x}=\frac{1}{e^{y}}=\frac{1}{x}.\]
Teorema\(\PageIndex{1}\)
Para cualquier número real\(x>0\),
\[\frac{d}{d x} \log (x)=\frac{1}{x}.\]
Ejemplo\(\PageIndex{7}\)
Ya que, para todos\(x>0\)
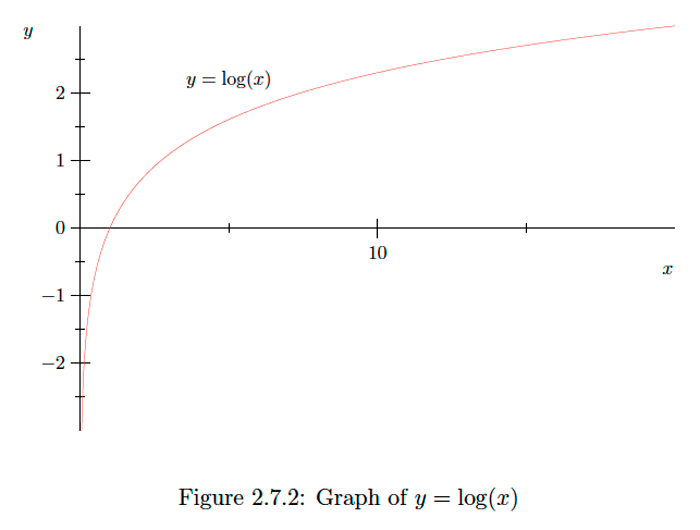
\[\frac{d}{d x} \log (x)=\frac{1}{x}>0\]y\[\frac{d^{2}}{d x^{2}} \log (x)=-\frac{1}{x^{2}}<0,\] la función\(y=\log (x)\) está aumentando\((0, \infty)\) y su gráfica es cóncava hacia abajo en\((0, \infty) .\) Ver Figura\(2.7 .2 .\)
Ejemplo\(\PageIndex{8}\)
Si\(f(x)=\log \left(x^{2}+1\right),\) entonces, usando la regla de la cadena,
\[f^{\prime}(x)=\frac{1}{x^{2}+1} \frac{d}{d x}\left(x^{2}+1\right)=\frac{2 x}{x^{2}+1}.\]
Ejercicio\(\PageIndex{7}\)
Encuentra la derivada de\(f(x)=\log (3 x+4)\).
- Contestar
-
\(f^{\prime}(x)=\frac{3}{3 x+4}\)
Ejercicio\(\PageIndex{8}\)
Encuentra la derivada de\(y=(x+1) \log (x+1)\).
- Contestar
-
\(\frac{d y}{d x}=1+\log (x+1)\)
Utilizando el teorema fundamental del cálculo, ahora se deduce que, para cualquier\(x>0\),
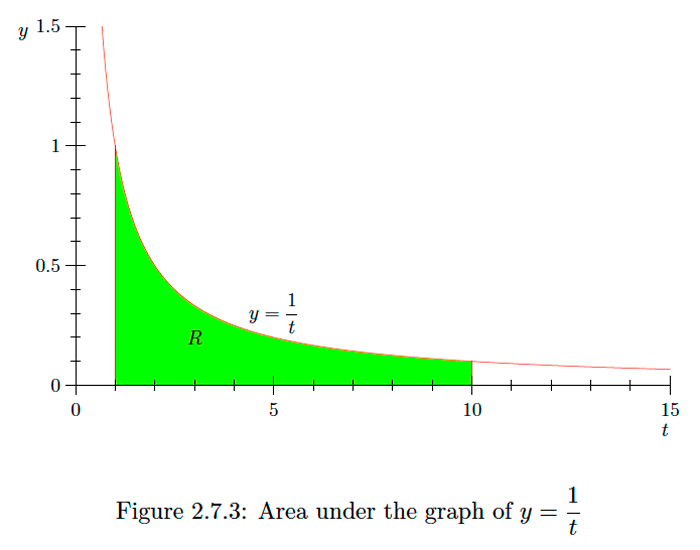
\[\int_{1}^{x} \frac{1}{t} d t=\left.\log (t)\right|_{1} ^{x}=\log (x)-\log (1)=\log (x).\]
Esto proporciona una interpretación geométrica del tronco (x) como el área bajo la gráfica\(y=\frac{1}{t}\) de 1 a\(x\). Por ejemplo,\(\log (10)\) es el área bajo la gráfica\(y=\frac{1}{t}\) de\(1 \text { to } 10 \text { (see Figure } 2.7 .3) .\)
Ejemplo\(\PageIndex{9}\)
Ahora podemos completar el ejemplo, discutido en el Ejemplo 2.5.8 y continuado en el Ejemplo 2.6 .19, de encontrar la longitud\(L\) de la gráfica de\(y=x^{2}\) sobre el intervalo\([0,1] .\) En esos ejemplos encontramos que
\[L=\int_{0}^{1} \sqrt{1+4 x^{2}} d x=\frac{\sqrt{5}}{2}+\frac{1}{4} \int_{1}^{2+\sqrt{5}} \frac{1}{w} d w .\]Ahora vemos eso\[\int_{1}^{2+\sqrt{5}} \frac{1}{w} d w=\left.\log (w)\right|_{1} ^{2+\sqrt{5}}=\log (2+\sqrt{5}),\] y así\[L=\frac{\sqrt{5}}{2}+\frac{1}{4} \log (2+\sqrt{5}).\] Redondeando a cuatro decimales, esto nos da\(L \approx 1.4789,\) la misma aproximación que obtuvimos en el Ejemplo 2.5.8. Tenga en cuenta, sin embargo, la ventaja de tener una impresión exacta para la respuesta: Podemos usar la expresión exacta\(L\) para aproximarnos fácilmente a cuantos dígitos queramos, mientras que no estamos seguros de la precisión de nuestro resultado aproximado original, y necesitaríamos recalcular la suma aproximada cada vez que quería tratar de mejorar nuestra precisión. Además, nuestro procedimiento para encontrar la expresión para\(L\) puede extenderse fácilmente para encontrar una expresión para la longitud de cualquier segmento de la parábola\(y=x^{2}\).
Ejemplo\(\PageIndex{10}\)
Evaluar
\[\int_{0}^{1} \frac{x}{1+x^{2}} d x,\]primero hacemos el cambio de variable\[\begin{aligned} u &=1+x^{2} \\ d u &=2 x d x. \end{aligned}\] Entonces\[\int_{0}^{1} \frac{x}{1+x^{2}} d x=\frac{1}{2} \int_{1}^{2} \frac{1}{u} d u=\left.\frac{1}{2} \log (u)\right|_{1} ^{2}=\frac{\log (2)}{2}.\]
Ejemplo\(\PageIndex{11}\)
Evaluando
\[\int_{1}^{10} \log (x) d x\]proporciona una interesante aplicación de integración por partes. Si dejamos\[\begin{aligned} u &=\log (x) & & d v=d x \\ d u &=\frac{1}{x} d x & & v=x, \end{aligned}\] entonces\[\int_{1}^{10} \log (x) d x=\left.x \log (x)\right|_{1} ^{10}-\int_{1}^{10} d x=10 \log (10)-9.\]
Ejemplo\(\PageIndex{12}\)
Podríamos usar el cambio de variable\(u=3 x+2\) para evaluar
\[\int_{0}^{5} \frac{4}{3 x+2} d x,\]o simplemente hacer la corrección apropiada para la regla de la cadena:\[\int_{0}^{5} \frac{4}{3 x+2} d x=\left.\frac{4}{3} \log (3 x+2)\right|_{0} ^{5}=\frac{4}{3}(\log (17)-\log (2))=\frac{4}{3} \log \left(\frac{17}{2}\right).\]
Ejercicio\(\PageIndex{9}\)
Evaluar\(\int_{0}^{2} \frac{1}{x+1} d x\).
- Contestar
-
\(\int_{0}^{2} \frac{1}{x+1} d x=\log (3)\)
Ejercicio\(\PageIndex{10}\)
Evaluar\(\int_{-1}^{2} \frac{x}{3 x^{2}+4} d x\).
- Contestar
-
\(\int_{-1}^{2} \frac{x}{3 x^{2}+4} d x=\frac{1}{6} \log \left(\frac{16}{7}\right)\)
Ejercicio\(\PageIndex{11}\)
Evaluar\(\int_{1}^{2} x \log (x) d x\).
- Contestar
-
\(\int_{1}^{2} x \log (x) d x=2 \log (2)-\frac{3}{4}\)
Ejercicio\(\PageIndex{12}\)
Evaluar\(\int_{-1}^{1} \sqrt{1+x^{2}} d x\).
- Contestar
-
\(\int_{-1}^{1} \sqrt{1+x^{2}} d x=\sqrt{2}+\log (1+\sqrt{2})\)
Ejercicio\(\PageIndex{13}\)
Evaluar\(\int_{-1}^{1} \frac{1}{\sqrt{1+x^{2}}} d x\).
- Contestar
-
\(\int_{-1}^{1} \frac{1}{\sqrt{1+x^{2}}} d x=2 \log (1+\sqrt{2})\)
Ahora es posible extender la regla de poder para diferenciar\(x^{n} .\) Supongamos que\(n \neq 0\) es un número real y señalar que, para\(x>0\),
\[x^{n}=e^{\log \left(x^{n}\right)}=e^{n \log (x)}.\]
Entonces
\[\begin{aligned} \frac{d}{d x} x^{n} &=\frac{d}{d x} e^{n \log (x)} \\ &=e^{n \log (x)} \frac{d}{d x} n \log (x) \\ &=\frac{n}{x} e^{n \log (x)} \\ &=\frac{n}{x} x^{n} \\ &=n x^{n-1} .\end{aligned}\]
Así tenemos nuestra forma final de la regla del poder.
Teorema\(\PageIndex{1}\)
Para cualquier número real\(n \neq 0,\) si\(x>0\),
\[\frac{d}{d x} x^{n}=n x^{n-1}.\]
Ejemplo\(\PageIndex{13}\)
Si\(f(x)=x^{\pi},\) entonces\(f^{\prime}(x)=\pi x^{\pi-1}\).
Ejercicio\(\PageIndex{14}\)
Encuentra
\[\frac{d}{d x} \pi^{x}\]por primera escritura\(\pi^{x}=e^{x \log (\pi)} .\) ¿Cómo se compara este resultado con el resultado del ejemplo anterior?
- Contestar
-
\(\frac{d}{d x} \pi^{x}=(\log (\pi)) \pi^{x}\)
2.7.3 Algunas aplicaciones
Como se mencionó al inicio de esta sección, existen muchas aplicaciones en las que se desea encontrar una función\(y\) que, para alguna constante\(k,\) satisfaga la ecuación diferencial
\[\frac{d y}{d t}=k y .\]
Tal ecuación surge siempre que la cantidad deseada crece, o disminuye, a una tasa que es proporcional a su valor actual. Como vimos anteriormente, una función de la forma
\[y=\alpha e^{k t}\]
satisface esta ecuación para cualquier constante real\(\alpha .\) Además, se puede demostrar que cualquier solución debe ser de esta forma.
Por ejemplo,\((2.7 .40)\) se utiliza para modelar la desintegración radiactiva. Es decir, si uno comienza con\(y_{0}\) gramos de un elemento radiactivo y\(y\) es la cantidad del elemento que queda después de\(t\) años, entonces hay alguna constante\(k\) (que depende del elemento particular que se esté considerando) para la cual
\[\frac{d y}{d t}=k y.\]
De ello se deduce que, para algún número real\(\alpha\),
\[y=\alpha e^{k t}.\]
Ya que se nos da que\(y=y_{0}\) cuando\(t=0,\) se deduce que
\[y_{0}=y(0)=\alpha e^{0}=\alpha.\]
De ahí
\[y=y_{0} e^{k t}.\]
Ahora supongamos que\(t_{1}<t_{2}\) son tales que\(y\) en el momento\(t_{2}\) es la mitad de\(y\) en el tiempo\(t_{1}\). Entonces
\[\frac{1}{2} y_{0} e^{k t_{1}}=y_{0} e^{k t_{2}}.\]
Así
\[e^{k t_{1}}=2 e^{k t_{2}},\]
y así
\[2=\frac{e^{k t_{1}}}{e^{k t_{2}}}=e^{k\left(t_{1}-t_{2}\right)}.\]
De ahí
\[\log (2)=\log \left(e^{k\left(t_{1}-t_{2}\right)}\right)=k\left(t_{1}-t_{2}\right),\]
de lo que se deduce que
\[t_{2}-t_{1}=-\frac{\log (2)}{k}.\]
Tenga en cuenta que el lado derecho de\((2.7 .50)\) no depende\(t_{1},\) y por lo tanto el tiempo requerido para que la mitad de un elemento radiactivo se profundice no depende de la cantidad inicial del elemento. Llamamos a este tiempo la vida media del elemento.
Por lo general, la tasa de desintegración de un elemento radiactivo se expresa en términos de su vida media. De\((2.7 .50),\) vemos que si la vida media de un elemento en particular es\(T,\) entonces la tasa de decaimiento del elemento es
\[k=-\frac{\log 2}{T}.\]
Ejemplo\(\PageIndex{14}\)
El carbono-14 es un isótopo radiactivo natural de carbono con una vida media de 5730 años. Un organismo vivo mantendrá constante nivel de carbono- el\(14,\) cual comenzará a desintegrarse uno el organismo muere y es enterrado. Debido a esto, la cantidad de carbono-14 en los restos de un organismo puede ser utilizada para estimar su edad. Por ejemplo, supongamos que un trozo de madera encontrado enterrado en un sitio arqueológico tiene\(14 \%\) de su carbono original-l4. Si\(T\) es el número de años desde que la madera fue enterrada y\(y_{0}\) es la cantidad original de carbono-14 en la madera, entonces
\[0.14 y_{0}=y_{0} e^{k T},\]donde, de\((2.7 .51)\),\[k=-\frac{\log (2)}{5730}.\] Se deduce que\(0.14=e^{k T},\) y así\[k T=\log (0.14).\] Así\[T=\frac{\log (0.14)}{k}=-\frac{5730 \log (0.14)}{\log (2)} \approx 16,253 \text { years. }\]
Ejercicio\(\PageIndex{15}\)
Supongamos que un trozo de madera enterrado en un sitio arqueológico tiene\(23 \%\) de su carbono original- ¿\(14 .\)Durante cuántos años se ha enterrado la madera?
- Contestar
-
\(12,149\)años
Ejercicio\(\PageIndex{16}\)
Supongamos que un elemento radiactivo tiene una vida media de\(24,065\) años. ¿Cuántos años tomará para que una muestra dada se desintegre hasta el punto\(10 \%\) de que solo quede la cantidad original?
- Contestar
-
\(79,942\)años
La ecuación diferencial sirve\((2.7 .40)\) también en algunas situaciones como un modelo sencillo de crecimiento poblacional. Supongamos, por ejemplo, que\(y\) es el tamaño de una población de una determinada especie de animal sobre un hábitat específico. A falta de límites extraños sobre el tamaño de la población (como una limitación en el suministro de alimentos, esperaríamos que la tasa de crecimiento de la población fuera proporcional a la población actual; es decir, esperaríamos\(y\) satisfacer\((2.7 .40)\) por alguna constante\(k\). En particular, si\(y_{0}\), el tamaño de la población en algún momento inicial y\(y\) es el tamaño de la población\(t\) año después, entonces
\[y=y_{0} e^{k t}.\]
Ahora supongamos que sabemos que la población está\(y_{1}\) en algún momento\(t_{1}>0 .\) Entonces
\[y_{1}=y_{0} e^{k t_{1}},\]
y así, después de dividirlo\(y_{0}\) y tomar el logaritmo de ambos lados,
\[k=\frac{1}{t_{1}} \log \left(\frac{y_{1}}{y_{0}}\right).\]
Ejemplo\(\PageIndex{15}\)
Supongamos que un determinado hábitat tiene inicialmente una población de 1000 venados, y que cinco años después la población ha crecido hasta los 1200 venados. Si dejamos\(y\) ser el tamaño de la población después de\(t\) años, y asumiendo que no hay limitaciones en el crecimiento de la población, habríamos
\[y=1000 e^{k t},\]donde\[k=\frac{1}{5} \log \left(\frac{1200}{1000}\right)=\frac{\log (1.2)}{5}.\] Entonces, por ejemplo, este modelo predeciría una población de\[\begin{aligned} y(10) &=1000 e^{10 k} \\ &=1000 e^{2 \log (1.2)} \\ &=1000 e^{\log \left(1.2^{2}\right)} \\ &=(1000)(1.2)^{2} \\ &=1440 \text { deer } \end{aligned}\] después de cinco años más.
Si\(y\) es el tamaño de una población de animales, llamamos a la ecuación diferencial
\[\frac{d y}{d t}=k y,\]
y la solución resultante,
\[y=y_{0} e^{k t},\]
el modelo de crecimiento natural. Aunque a menudo es relativamente preciso en intervalos de tiempo pequeños, este modelo es claramente poco realista para cualquier período de tiempo prolongado, ya que predice un crecimiento ilimitado. Incluso en la mejor de las situaciones, otros factores, como la disponibilidad de alimentos y refugio, eventualmente entrarán en juego.
El modelo logístico introduce una variación en el modelo básico\((2.7 .40)\) que influye en el efecto limitante del espacio y la comida. En este caso, suponemos que existe un límite superior, digamos\(M\), al tamaño de la población que el hábitat puede sostener y que la tasa de crecimiento de la población disminuye a medida que el tamaño de la población se acerca a este valor limitante. Más precisamente, que\(k\) sea la tasa natural de crecimiento de la población, es decir, la tasa de crecimiento si no hay factores limitantes, o cuando el tamaño de la población es pequeño comparado con\(M,\) y deja\(y\) ser el tamaño de la población en el momento\(t .\) Entonces suponemos\(k\) se disminuye por un factor de\(1-\frac{y}{M},\) esto es, la proporción de espacio que queda para el crecimiento. La ecuación diferencial resultante para el modelo logístico es
\[\frac{d y}{d t}=k y\left(1-\frac{y}{M}\right)=\frac{k}{M} y(M-y)=\beta y(M-y),\]
donde\(\beta=\frac{k}{M}\).
Para resolverlo\((2.7 .57),\) primero lo reescribimos usando\(s\) para la variable independiente, es decir, como
\[\frac{d y}{d s}=\beta y(M-y),\]
y luego dividirlo a través de ambos lados\(y(M-y)\) para obtener
\[\frac{1}{y(M-y)} \frac{d y}{d s}=\beta.\]
A continuación, integramos ambos lados de esta ecuación de 0 a algún tiempo fijo\(t:\)
\[\int_{0}^{t} \frac{1}{y(M-y)} \frac{d y}{d s} d s=\int_{0}^{t} \beta d s.\]
Para el lado derecho de\((2.7 .60),\) tenemos simplemente
\[\int_{0}^{t} \beta d s=\beta t.\]
Para el lado izquierdo, comenzamos con el cambio de variable
\[\begin{aligned} u &=y \\ d u &=\frac{d y}{d s} d s, \end{aligned}\]
de la que obtenemos
\[\int_{0}^{t} \frac{1}{y(M-y)} \frac{d y}{d s} d s=\int_{y_{0}}^{y} \frac{1}{u(M-u)} d u,\]
donde nuevamente hemos utilizado\(y_{0}\) para denotar el tamaño de la población en el momento\(s=0\) (y señalando que\(y\) es el tamaño de la población cuando\(s=t\)). Suponemos\(0<y<M ;\) que\(0<y_{0}<M\) y es decir, asumimos que las poblaciones involucradas son positivas y no superan la población máxima sustentable.
Para evaluar\((2.7 .63),\) nos basamos en un resultado que involucra lo que se conoce como descomposiciones parciales de fracciones: Existen números reales\(A\) y\(B\) tales que
\[\frac{1}{u(M-u)}=\frac{A}{u}+\frac{B}{M-u}.\]
Para encontrar\(A\) y\(B,\) señalamos que\((2.7 .64)\) implica que
\[\frac{1}{u(M-u)}=\frac{A(M-u)}{u(M-u)}+\frac{B u}{u(M-u)}=\frac{A(M-u)+B u}{u(M-u)}.\]
De ello se deduce que, para todos los valores de\(u\),
\[1=A(M-u)+B u.\]
En particular, cuando\(u=0\) tenemos\(1=A M,\) y cuando\(u=M\) tenemos\(1=B M\) .De ahí
\[A=\frac{1}{M} \text { and } B=\frac{1}{M},\]
y así
\[\frac{1}{u(M-u)}=\frac{1}{M} \frac{1}{u}+\frac{1}{M} \frac{1}{M-u}.\]
De ahí que ahora tenemos
\[\begin{aligned} \int_{y_{0}}^{y} \frac{1}{u(M-u)} d u &=\frac{1}{M} \int_{y_{0}}^{y} \frac{1}{u} d u+\frac{1}{M} \int_{y_{0}}^{y} \frac{1}{M-u} d u \\ &=\left.\frac{1}{M} \log (u)\right|_{y_{0}} ^{y}-\left.\frac{1}{M} \log (M-u)\right|_{y_{0}} ^{y} \\ &=\frac{1}{M}\left(\log (y)-\log \left(y_{0}\right)-\log (M-y)\right.\\ &=\frac{1}{M} \log \left(\frac{y\left(M-y_{0}\right)}{y_{0}(M-y)}\right). \end{aligned}\]
Combinando\((2.7 .60),(2.7 .61),\) y\((2.7 .69),\) tenemos
\[\beta M t=\log \left(\frac{y\left(M-y_{0}\right)}{y_{0}(M-y)}\right),\]
que ahora necesitan resolver para\(y .\) Para comenzar, exponenciar ambas partes para obtener
\[e^{\beta M t}=\frac{y\left(M-y_{0}\right)}{y_{0}(M-y)}.\]
De ello se deduce que
\[y\left(M-y_{0}\right)=e^{\beta M t} y_{0}(M-y)=y_{0} M e^{\beta M t}-y_{0} y e^{\beta M t},\]
y así
\[y_{0} M e^{\beta M t}=y\left(M-y_{0}\right)+y_{0} y e^{\beta M t}=\left(M+y_{0}\left(e^{\beta M t}-1\right)\right) y.\]
Así
\[y=\frac{y_{0} M e^{\beta M t}}{\left(M+y_{0}\left(e^{\beta M t}-1\right)\right)}.\]
Si dividimos el numerador y denominador del lado derecho por\(e^{\beta M t},\) tenemos
\[y=\frac{y_{0} M}{M e^{-\beta M t}+y_{0}-y_{0} e^{-\beta M t}},\]
de la que obtenemos nuestra forma final
\[y=\frac{y_{0} M}{y_{0}+\left(M-y_{0}\right) e^{-\beta M t}}.\]
Obsérvese que cuando se\(t=0,(2.7 .76)\) reduce a\(y=y_{0},\) como debiera dada nuestra condición inicial, y cuando\(t\) es infinito,\(e^{-\beta M t} \simeq 0,\) y así\(y=M .\) pues\(y_{0} \leq y<M\) para todos\(t,\) con\(y\) acercarse a\(M\) medida que\(t\) crece.
Recordando que\(\beta=\frac{k}{M},\) donde\(k\) está la tasa natural de crecimiento de la población, podemos reescribir\((2.7 .76)\) como
\[y=\frac{y_{0} M}{y_{0}+\left(M-y_{0}\right) e^{-k t}}.\]
Ejemplo\(\PageIndex{16}\)
En nuestro ejemplo anterior, donde\(y\) representaba el número de venados en un determinado hábitat después de\(t\) años, encontramos
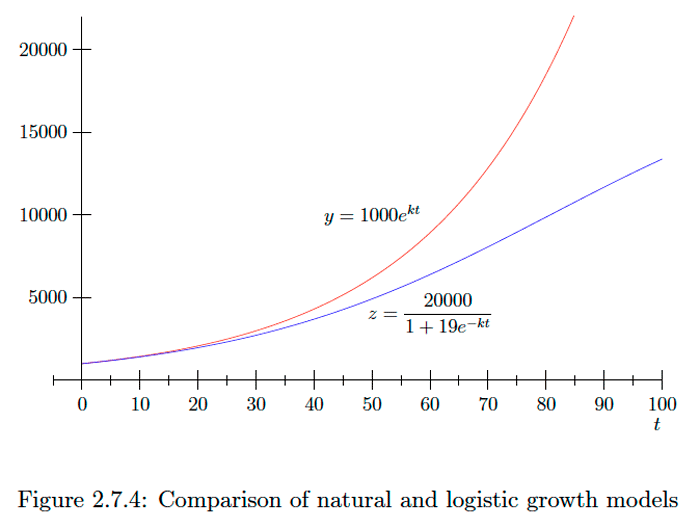
\[k=\frac{\log (1.2)}{5}.\]Ahora supongamos que el hábitat no soporta más que los\(20,000\) venados. Entonces el modelo logístico nos daría\[z=\frac{(1000)(20000)}{1000+(20000-1000) e^{k t}}=\frac{20000}{1+19 e^{-k t}}\] por el número de venados después de\(t\) años. Después de diez años, este modelo predeciría una población\[z(10)=\frac{20000}{1+19 e^{-10 k}} \approx 1409 \mathrm{deer},\] sólo ligeramente inferior a la 1440 predicha por el modelo de crecimiento natural. Sin embargo, las diferencias entre los dos modelos se vuelven más pronunciadas con el tiempo. Por ejemplo, después de cuarenta años, el modelo de crecimiento natural predice\[y(40)=1000 e^{40 k} \approx 4300 \text { deer, }\]
mientras que el modelo logístico predice
\[z(40)=\frac{20000}{1+19 e^{-40 k}} \approx 3691 \mathrm{deer}\]y en 100 años, el modelo de crecimiento natural predice\[y(100)=1000 e^{100 k} \approx 38338 \mathrm{ deer},\] mientras que el modelo logístico predice solo Por\[z(100)=\frac{20000}{1+19 e^{-100 k}} \approx 13373 \text { deer. }\] supuesto, con el tiempo el modelo de crecimiento natural predice una población que crece sin ningún límite, mientras que el modelo logístico predice que la población, si bien siempre va en aumento, nunca supere\(20,000 .\) Ver Figura\(2.7 .4 .\)
En la evaluación se\((2.7 .63)\) utilizó una descomposición parcial de la fracción. Más generalmente, supongamos\(p\) y\(q\) son polinomios, el grado de\(p\) es menor que el grado de\(q,\) y\(q\) factores completamente en distinet factores lineales, digamos,
\[q(x)=\left(a_{1} x+b_{1}\right)\left(a_{2} x+b_{2}\right) \cdots\left(a_{n} x+b_{n}\right).\]
Entonces se puede demostrar que existen consentimientos\(A_{1}, A_{2}, \ldots, A_{n}\) para los cuales
\[\frac{p(x)}{q(x)}=\frac{A_{1}}{a_{1} x+b_{2}}+\frac{A_{2}}{a_{2} x+b_{2}}+\cdots+\frac{A_{n}}{a_{n} x+b_{n}}.\]
La evaluación de
\[\int_{a}^{b} \frac{p(x)}{q(x)} d x,\]
para cualquier número real\(a\) y\(b\) para el cual\(q(x) \neq 0\) para todos\(x\) en\([a, b],\) entonces sigue fácilmente.
Ejemplo\(\PageIndex{17}\)
Evaluar
\[\int_{0}^{1} \frac{x}{x^{2}-4} d x,\]primero señalamos que, ya que\(x^{2}-4=(x-2)(x+2),\) existen constantes\(A\) y\(B\) para las cuales se\[\frac{x}{x^{2}-4}=\frac{A}{x-2}+\frac{B}{x+2}.\] deduce que\[\frac{x}{x^{2}-4}=\frac{A(x+2)+B(x-2)}{x^{2}-4},\] y así\[x=A(x+2)+B(x-2)\] para todos los valores de\(x\). En particular, cuando\(x=2\) tenemos\(2=4 A,\) y cuando\(x=-2\) tenemos\(-2=-4 B .\) De ahí\(A=\frac{1}{2}\) y así\(B=\frac{1}{2},\)\[\frac{x}{x^{2}-4}=\frac{1}{2} \frac{1}{x-2}+\frac{1}{2} \frac{1}{x+2}.\] Y así tenemos\[\int_{0}^{1} \frac{x}{x^{2}-4} d x=\frac{1}{2} \int_{0}^{1} \frac{1}{x-2} d x+\frac{1}{2} \int_{0}^{1} \frac{1}{x+2} d x.\] Ahora\[\frac{1}{2} \int_{0}^{1} \frac{1}{x+2} d x=\left.\frac{1}{2} \log (x+2)\right|_{0} ^{1}=\frac{1}{2}(\log (3)-\log (2)),\] pero la primera integral requiere un poco más de cuidado porque\(x-2<0\)\(0 \leq x \leq 1\) para.Si hacemos el cambio de variables,\[\begin{aligned} u &=-(x-2) \\ d u &=-d x, \end{aligned}\] entonces, ya que\(x-2=-u\),\[\begin{aligned} \frac{1}{2} \int_{0}^{1} \frac{1}{x-2} d x &=\frac{1}{2} \int_{2}^{1} \frac{1}{u} d u \\ &=-\frac{1}{2} \int_{1}^{2} \frac{1}{u} d u \\ &=-\left.\frac{1}{2} \log (u)\right|_{1} ^{2} \\ &=-\frac{1}{2} \log (2). \end{aligned}\] Por lo tanto\[\int_{0}^{1} \frac{x}{x^{2}-1} d x=\frac{1}{2}(\log (3)-\log (2))-\frac{1}{2} \log (2)=\frac{1}{2} \log (3)-\log (2).\]
Ejercicio\(\PageIndex{19}\)
Evaluar\(\int_{-2}^{2} \frac{1}{9-x^{2}} d x\).
- Contestar
-
\(\int_{-2}^{2} \frac{1}{9-x^{2}} d x=\frac{1}{3} \log (5)\)
Ejercicio\(\PageIndex{20}\)
Evaluar\(\int_{0}^{1} \frac{x+4}{x^{2}+3 x+2} d x\).
- Contestar
-
\(\int_{0}^{1} \frac{x+14}{x^{2}+3 x+2} d x=5 \log (2)-2 \log (3)\)


