2.6: Algunas técnicas para evaluar integrales

2.6.1 Cambio de Variable

Si$F$ es una integral de$f$ y$\varphi$ es una función diferenciable, entonces, usando la regla de la cadena,

$$\frac{d}{d x} F(\varphi(x))=F^{\prime}(\varphi(x)) \varphi^{\prime}(x)=f(\varphi(x)) \varphi^{\prime}(x).$$

Escrito en términos de integrales, tenemos

$$\int f(\varphi(x)) \varphi^{\prime}(x) d x=F(\varphi(x))+c.$$

Si dejamos$u=\varphi(x)$ y notamos que

$$\int f(u) d u=F(u)+c,$$

podemos expresarnos$(2.6.2)$ como

$$\int f(\varphi(x)) \varphi^{\prime}(x) d x=\int f(u) d u.$$

Es decir, podemos evaluar

$$\int f(\varphi(x)) \varphi^{\prime}(x) d x,$$

cambiando la variable a$u=\varphi(x),$ con$\varphi^{\prime}(x) d x$ devenir$d u$ desde

$$\frac{d u}{d x}=\varphi^{\prime}(x).$$

Ejemplo$\PageIndex{1}$

Evaluar

$$\int 2 x \sqrt{1+x^{2}} d x,$$

dejar

$$\begin{aligned} u &=1+x^{2} \\ d u &=2 x d x. \end{aligned}$$

Entonces

$$\int 2 x \sqrt{1+x^{2}} d x=\int \sqrt{u} d u=\frac{2}{3} u^{\frac{3}{2}}+c=\frac{2}{3}\left(1+x^{2}\right)^{\frac{3}{2}}+c.$$

Ejemplo$\PageIndex{2}$

Evaluar

$$\int x \sin \left(x^{2}\right) d x,$$

dejar

$$\begin{aligned} u &=x^{2} \\ d u &=2 x d x \end{aligned}$$

Tenga en cuenta que en este caso no podemos hacer una sustitución directa de$u$ y$d u$ ya que$d u=2 x d x$ no aparece como parte de la integral. Sin embargo,$d u$ difiere$x d x$ de solo un factor constante, y podemos reescribir$d u=2 x d x$ como

$$\frac{1}{2} d u=x d x.$$

Ahora podemos realizar el cambio de variable:

$$\int x \sin (u) d x=\frac{1}{2} \int \sin (u) d u=-\frac{1}{2} \cos (u)+c=-\frac{1}{2} \cos \left(x^{2}\right)+c.$$

Ejemplo$\PageIndex{3}$

Tenga en cuenta que podríamos evaluar la integral

$$\int \cos (4 x) d x$$

usando la sustitución

$$\begin{aligned} u &=4 x \\ d u &=4 d x, \end{aligned}$$

lo que nos da

$$\int \cos (4 x) d x=\frac{1}{4} \int \cos (u) d u=\frac{1}{4} \sin (u)+c=\frac{1}{4} \sin (4 x)+c.$$

Sin embargo, probablemente sea más rápido, y más fácil, adivinar que la integral de$\cos (4 x)$ debe estar cerca$\sin (4 x),$ y luego corregir esta suposición apropiadamente después de señalar que

$$\frac{d}{d x} \sin (4 x)=4 \cos (4 x).$$

Ejemplo$\PageIndex{4}$

Evaluar

$$\int \cos ^{2}(5 x) \sin (5 x) d x,$$

dejar

$$\begin{aligned} u &=\cos (5 x) \\ d u &=-5 \sin (5 x) d x \end{aligned}.$$

Entonces

$$\int \cos ^{2}(5 x) \sin (5 x) d x=-\frac{1}{5} \int u^{2} d u=-\frac{1}{15} u^{3}+c=-\frac{1}{15} \cos ^{3}(5 x)+c.$$

Consideremos ahora la integral definitiva

$$\int_{a}^{b} f(\varphi(x)) \varphi^{\prime}(x) d x.$$

Si$F$ es una integral de$f, c=\varphi(a),$ y$d=\varphi(b),$ entonces es $$\begin{aligned} \int_{a}^{b} f(\varphi(x)) \varphi^{\prime}(x) d x &=F(\varphi(x)))_{a}^{b} \\ &=F(\varphi(b))-F(\varphi(a)) \\ &=F(d)-F(c) \\ &=\left.F(u)\right|_{c} ^{d} \\ &=\int_{c}^{d} f(u) d u .\end{aligned}$$ decir, podemos usar un cambio de variable para evaluar una integral definida de la misma manera que anteriormente, siendo la única diferencia que debemos cambiar los límites de integración para reflejar los valores de la nueva variable$u .$

Ejemplo$\PageIndex{5}$

Evaluar

$$\int_{0}^{1} \frac{x}{\sqrt{1+x^{2}}} d x,$$ let $$\begin{aligned} u &=1+x^{2} \\ d u &=2 x d x. \end{aligned}$$ Tenga en cuenta que cuando$x=0, u=1,$ y cuando$x=1, u=2 .$ Por lo tanto $$\int_{0}^{1} \frac{x}{\sqrt{1+x^{2}}} d x=\frac{1}{2} \int_{1}^{2} \frac{1}{\sqrt{u}} d u=\left.\sqrt{u}\right|_{1} ^{2}=\sqrt{2}-1.$$

Ejemplo$\PageIndex{6}$

Evaluar

$$\int_{0}^{\frac{\pi}{4}} \cos ^{2}(2 x) \sin (2 x) d x,$$ let $$\begin{aligned} u &=\cos (2 x) \\ d u &=-2 \sin (2 x) d x. \end{aligned}$$ $$\int_{0}^{\frac{\pi}{4}} \cos ^{2}(2 x) \sin (2 x) d x=-\frac{1}{2} \int_{1}^{0} u^{2} d u.$$ Tenga en cuenta que, después de hacer el cambio de variable, el límite superior de integración es menor que el límite inferior de integración, situación no cubierta por nuestra definición de la integral definida o nuestra afirmación del teorema fundamental del cálculo. Sin embargo, el resultado sobre las sustituciones anteriores muestra que obtendremos el resultado correcto si aplicamos el teorema fundamental como de costumbre. Además, esto apunta hacia una extensión de nuestra definición: si$b<a,$ entonces deberíamos tener $$\int_{a}^{b} f(x) d x=-\int_{b}^{a} f(x) d x,$$ lo que es consistente tanto con el teorema fundamental del cálculo como con la definición de la integral definida (ya que, si$b<a, d x=\frac{b-a}{N}<0$ por cualquier entero infinito positivo$N) .$ Con esto, podemos terminar la evaluación: $$\int_{0}^{\frac{\pi}{4}} \cos ^{2}(2 x) \sin (2 x) d x=-\frac{1}{2} \int_{1}^{0} u^{2} d u=\frac{1}{2} \int_{0}^{1} u^{2} d u=\left.\frac{u^{3}}{6}\right|_{0} ^{1}=\frac{1}{6}.$$

Ejercicio$\PageIndex{1}$

Evaluar$\int 3 x^{2} \sqrt{1+x^{3}} d x$.

Contestar

$\int 3 x^{2} \sqrt{1+x^{3}} d x=\frac{2}{3}\left(1+x^{3}\right)^{\frac{3}{2}}+c$

Ejercicio$\PageIndex{2}$

Evaluar$\int x \sqrt{4+3 x^{2}} d x$.

Contestar

$\int x \sqrt{4+3 x^{2}} d x=\frac{1}{9}\left(4+3 x^{2}\right)^{\frac{3}{2}}+c$

Ejercicio$\PageIndex{3}$

Evaluar$\int \sec ^{2}(3 x) \tan ^{2}(3 x) d x$.

Contestar

$\int \sec ^{2}(4 x) \tan ^{2}(4 x) d x=\frac{1}{12} \tan ^{3}(4 x)+c$

Ejercicio$\PageIndex{4}$

Evaluar$\int_{0}^{2} \frac{x}{\sqrt{4+x^{2}}} d x$.

Contestar

$\int_{0}^{2} \frac{x}{\sqrt{4+x^{2}}} d x=2 \sqrt{2}-2$

Ejercicio$\PageIndex{5}$

Evaluar$\int_{0}^{\frac{\pi}{6}} \sin (3 x) d x$.

Contestar

$\int_{0}^{\frac{\pi}{2}} \sin (3 x) d x=\frac{2}{3}$

Ejercicio$\PageIndex{6}$

Evaluar$\int_{0}^{\frac{\pi}{2}} \sin ^{4}(2 x) \cos (2 x) d x$.

Contestar

$\int_{0}^{\frac{\pi}{4}} \sin ^{4}(2 x) \cos (2 x) d x=\frac{1}{10}$

2.6.2 Integración por Partes

Supongamos$u$ y$v$ son ambas funciones diferenciables de$x .$ Since, por la regla del producto,

$$\frac{d}{d x} u v=u \frac{d v}{d x}+v \frac{d u}{d x},$$ tenemos $$u \frac{d v}{d x}=\frac{d}{d x} u v-v \frac{d u}{d x}.$$ Por lo tanto, integrar ambos lados con respecto a$x$, $$\int u \frac{d v}{d x} d x=\int \frac{d}{d x} u v-\int v \frac{d u}{d x}=u v-\int v \frac{d u}{d x} d x,$$ que podemos escribir como $$\int u d v=u v-\int v d u.$$ Esta última formulación, conocida como integración por partes, es útil siempre que la integral a la derecha de$(2.6 .10)$ sea de alguna manera más simple que la integral de la izquierda. Los siguientes ejemplos ilustrarán algunos casos típicos.

Ejemplo$\PageIndex{7}$

Considerar la integral

$$\int x \cos (x) d x.$$ Si dejamos$u=x$ y$d v=\cos (x) d x,$ entonces$d u=d x$ y podemos dejar$v=\sin (x)$. Tenga en cuenta que tenemos alguna opción$v$ ya que el único requisito es que sea una integral de$\cos (x) .$ Uso que$(2.6 .10),$ tenemos $$\int x \sin (x) d x=u v-\int v d u=x \sin (x)-\int \sin (x) d x=x \sin (x)+\cos (x)+c.$$ Al evaluar una integral definida usando integración por partes, debemos recordar evaluar cada pieza de la integral. Es decir, $$\int u d v=\left.u v\right|_{a} ^{b}-\int_{a}^{b} v d u.$$

Ejemplo$\PageIndex{8}$

Evaluar

$$\int_{0}^{\pi} x^{2} \sin (x) d x,$$ let $$\begin{aligned} u &=x^{2} & & d v=\sin (x) d x \\ d u &=2 x d x & & v=-\cos (x). \end{aligned}$$ Entonces, usando$(2.6.11)$, $$\int_{0}^{\pi} x^{2} \sin (x) d x=-\left.x^{2} \cos (x)\right|_{0} ^{\pi}+\int_{0}^{\pi} 2 x \cos (x) d x=\pi^{2}+\int_{0}^{\pi} 2 x \cos (x) d x.$$ $$\begin{aligned} u &=2 x & & d v=\cos (x) \\ d u &=2 d x & & v=\sin (x), \end{aligned}$$ tenemos $$\begin{aligned} \int_{0}^{\pi} x^{2} \sin (x) d x &=\pi^{2}+\left.2 x \sin (x)\right|_{0} ^{\pi}-\int_{0}^{\pi} 2 \sin (x) d x \\ &=\pi^{2}+(0-0)+\left.2 \cos (x)\right|_{0} ^{\pi} \\ &=\pi^{2}-2-2 \\ &=\pi^{2}-4. \end{aligned}$$

Ejemplo$\PageIndex{9}$

Evaluar

$$\int_{0}^{1} x \sqrt{1+x} d x,$$ let $$\begin{aligned} u &=x & & d v=\sqrt{1+x} d x \\ d u &=d x & & v=\frac{2}{3}(1+x)^{\frac{3}{2}} .\end{aligned}$$ Entonces $$\begin{aligned} \int_{0}^{1} x \sqrt{1+x} d x &=\left.\frac{2}{3} x(1+x)^{\frac{3}{2}}\right|_{0} ^{1}-\frac{2}{3} \int_{0}^{1}(1+x)^{\frac{3}{2}} d x \\ &=\frac{4 \sqrt{2}}{3}-\left.\frac{4}{15}(1+x)^{\frac{5}{2}}\right|_{0} ^{1} \\ &=\frac{4 \sqrt{2}}{3}-\frac{16 \sqrt{2}-4}{15} \\ &=\frac{4 \sqrt{2}+4}{15}. \end{aligned}$$

Ejercicio$\PageIndex{7}$

Evaluar$\int x \sin (2 x) d x$.

Contestar

$\int x \sin (2 x) d x=-\frac{1}{2} x \cos (2 x)+\frac{1}{4} \sin (2 x)+c$

Ejercicio$\PageIndex{8}$

Evaluar$\int x^{2} \cos (3 x) d x$.

Contestar

$\int x^{2} \cos (3 x) d x=\frac{1}{3} x^{2} \sin (3 x)+\frac{2}{9} x \cos (3 x)-\frac{2}{27} \sin (3 x)+c$

Ejercicio$\PageIndex{9}$

Evaluar$\int_{0}^{\pi} x \cos \left(\frac{1}{2} x\right) d x$.

Contestar

$\int_{0}^{\pi} x \cos \left(\frac{1}{2} x\right) d x=2 \pi-4$

Ejercicio$\PageIndex{10}$

Evaluar$\int_{0}^{\frac{\pi}{2}} 3 x^{2} \cos \left(x^{2}\right) d x$.

Contestar

$\int_{0}^{\frac{\pi}{2}} 3 x^{2} \cos \left(x^{2}\right) d x=-6 \pi$

Ejercicio$\PageIndex{11}$

Evaluar$\int_{0}^{2} x^{2} \sqrt{1+x} d x$.

Contestar

$\int_{0}^{2} x^{2} \sqrt{1+x} d x=\frac{264 \sqrt{3}-16}{105}$

2.6.3 Algunas integrales que involucran funciones trigonométricas

Los siguientes ejemplos ilustrarán cómo diversas identidades son útiles para simplificar algunas integrales que involucran funciones trigonométricas.

Ejemplo$\PageIndex{10}$

Evaluar la integral

$$\int_{0}^{\pi} \sin ^{2}(x) d x,$$ usaremos la fórmula de medio ángulo: $$\sin ^{2}(x)=\frac{1-\cos (2 x)}{2}.$$ Entonces $$\begin{aligned} \int_{0}^{\pi} \sin ^{2}(x) d x &=\frac{1}{2} \int_{0}^{\pi}(1-\cos (2 x)) d x \\ &=\left.\frac{1}{2} x\right|_{0} ^{\pi}-\left.\frac{1}{4} \sin (2 x)\right|_{0} ^{\pi} \\ &=\frac{\pi}{2} .\end{aligned}$$

También hay una fórmula de medio ángulo para el coseno, a saber,

$$\cos ^{2}(x)=\frac{1+\cos (2 x)}{2}.$$

Como se ilustra en el siguiente ejemplo, podemos usar las fórmulas de medio ángulo recursivamente para evaluar la integral de cualquier potencia par de seno o coseno.

Ejemplo$\PageIndex{11}$

Usando 2.6 .13 dos veces, tenemos

$$\begin{aligned} \int_{0}^{\pi} \cos ^{4}(3 x) d x &=\int_{0}^{\pi}\left(\cos ^{2}(3 x)\right)^{2} d x \\ &=\int_{0}^{\pi}\left(\frac{1}{2}(1+\cos (6 x))\right)^{2} d x \\ &=\frac{1}{4} \int_{0}^{\pi}\left(1+2 \cos (6 x)+\cos ^{2}(6 x)\right) d x \\ &=\left.\frac{1}{4} x\right|_{0} ^{\pi}+\left.\frac{1}{12} \sin (6 x)\right|_{0} ^{\pi}+\frac{1}{8} \int_{0}^{\pi}(1+\cos (12 x)) d x \\ &=\frac{\pi}{4}+\left.\frac{1}{8} x\right|_{0} ^{\pi}+\left.\frac{1}{96} \sin (12 x)\right|_{0} ^{\pi} \\ &=\frac{3 \pi}{8} . \end{aligned}$$

Ejercicio$\PageIndex{12}$

Evaluar$\int_{0}^{\pi} \sin ^{2}(2 x) d x$.

Contestar

$\int_{0}^{\pi} \sin ^{2}(2 x) d x=\frac{\pi}{2}$

Ejercicio$\PageIndex{13}$

Evaluar$\int_{0}^{\pi} \cos ^{2}(3 x) d x$.

Contestar

$\int_{0}^{\pi} \cos ^{2}(3 x) d x=\frac{\pi}{2}$

Ejercicio$\PageIndex{14}$

Evaluar$\int \cos ^{4}(x) d x$.

Contestar

$\int \cos ^{4}(x) d x=\frac{3}{8} x+\frac{1}{4} \sin (2 x)+\frac{1}{32} \sin (4 x)+c$

El siguiente ejemplo ilustra una fórmula de reducción.

Ejemplo$\PageIndex{12}$

Supongamos que$n \geq 2$ es un entero y queremos evaluar

$$\int_{0}^{\pi} \sin ^{n}(x) d x.$$ Comenzamos con una integración por partes: si dejamos $$\begin{aligned} u &=\sin ^{n-1}(x) & & d v=\sin (x) d x \\ d u &=(n-1) \sin ^{n-2}(x) \cos (x) d x & & v=-\cos (x), \end{aligned}$$ entonces $$\begin{aligned} \int_{0}^{\pi} \sin ^{n}(x) d x &=-\left.\sin ^{n-1}(x) \cos (x)\right|_{0} ^{\pi}+(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) \cos ^{2}(x) d x \\ &=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) \cos ^{2}(x) d x . \end{aligned}$$ Ahora$\cos ^{2}(x)=1-\sin ^{2}(x),$ así tenemos $$\begin{aligned} \int_{0}^{\pi} \sin ^{n}(x) d x &=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x)\left(1-\sin ^{2}(x)\right) d x \\ &=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) d x-(n-1) \int_{0}^{\pi} \sin ^{n}(x) d x . \end{aligned}$$ Aviso que$\int_{0}^{\pi} \sin ^{n}(x) d x$ ocurre en ambos lados de esta ecuación. De ahí que podamos resolver para esta cantidad, primero obteniendo $$n \int_{0}^{\pi} \sin ^{n}(x) d x=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) d x,$$ y después $$\int_{0}^{\pi} \sin ^{n}(x) d x=\frac{n-1}{n} \int_{0}^{\pi} \sin ^{n-2}(x) d x.$$ Observar que, aunque aún no hemos encontrado el valor de nuestra integral, hemos reducido el poder de$\sin (x)$ en la integral. Ahora podemos usar$(2.6 .14)$ repetidamente para reducir el poder de$\sin (x)$ hasta que podamos evaluar fácilmente la integral resultante. Por ejemplo, si$n=6$ tenemos $$\begin{aligned} \int_{0}^{\pi} \sin ^{6}(x) d x &=\frac{5}{6} \int_{0}^{\pi} \sin ^{4}(x) d x \\ &=\frac{5}{6} \frac{3}{4} \int_{0}^{\pi} \sin ^{2}(x) d x \\ &=\frac{5}{6} \frac{3}{4} \frac{1}{2} \int_{0}^{\pi} d x \\ &=\frac{5 \pi}{16} . \end{aligned}$$ Similarmente, $$\begin{aligned} \int_{0}^{\pi} \sin ^{5}(x) d x &=\frac{4}{5} \int_{0}^{\pi} \sin ^{3}(x) d x \\ &=\frac{4}{5} \frac{2}{3} \int_{0}^{\pi} \sin (x) d x \\ &=-\left.\frac{8}{15} \cos (x)\right|_{0} ^{\pi} \\ &=\frac{16}{15} . \end{aligned}$$

Ejercicio$\PageIndex{15}$

Utilice la fórmula de reducción (2.6.14) para evaluar

$$\int_{0}^{\pi} \sin ^{8}(x) d x .$$

Contestar

$\int_{0}^{\pi} \sin ^{8}(x) d x=\frac{35 \pi}{128}$

Ejercicio$\PageIndex{16}$

Utilice la fórmula de reducción$(2.6.14)$ para evaluar

$$\int_{0}^{\pi} \sin ^{7}(x) d x .$$

Contestar

$\int_{0}^{\pi} \sin ^{7}(x) d x=\frac{32}{35}$

Ejercicio$\PageIndex{17}$

Derivar la fórmula de reducción

$$\int_{0}^{\pi} \cos ^{n}(x)=\frac{n-1}{n} \int_{0}^{\pi} \cos ^{n-2}(x) d x ,$$ donde$n \geq 2$ es un entero.

Ejercicio$\PageIndex{18}$

Utilizar la fórmula de reducción del ejercicio anterior para evaluar

$$\int_{0}^{\pi} \cos ^{6}(x) d x .$$

Contestar

$\int_{0}^{\pi} \cos ^{6}(x) d x=\frac{5 \pi}{16}$

Ejercicio$\PageIndex{19}$

Derivar las fórmulas de reducción

$$\int \sin ^{n}(x) d x=-\frac{1}{n} \sin ^{n-1}(x) \cos (x)+\frac{n-1}{n} \int \sin ^{n-2}(x) d x$$ y $$\int \cos ^{n}(x) d x=\frac{1}{n} \cos ^{n-1}(x) \sin (x)+\frac{n-1}{n} \int \cos ^{n-2}(x) d x ,$$ donde$n \geq 2$ es un entero.

Ejemplo$\PageIndex{13}$

Una alternativa al uso de una fórmula de reducción en el último ejemplo comienza con señalar que

$$\begin{aligned} \int_{0}^{\pi} \sin ^{5}(x) d x &=\int_{0}^{\pi} \sin ^{4}(x) \sin (x) d x \\ &=\int_{0}^{\pi}\left(\sin ^{2}(x)\right)^{2} \sin (x) d x \\ &=\int_{0}^{\pi}\left(1-\cos ^{2}(x)\right)^{2} \sin (x) d x \\ &=\int_{0}^{\pi}\left(1-2 \cos ^{2}(x)+\cos ^{4}(x)\right) \sin (x) d x . \end{aligned}$$ Esta última integral ahora puede ser evaluada utilizando el cambio de variable que nos $$\begin{aligned} u &=\cos (x) \\ d u &=-\sin (x) d x , \end{aligned}$$ da $$\begin{aligned} \int_{0}^{\pi} \sin ^{5}(x) d x &=-\int_{1}^{-1}\left(1-2 u^{2}+u^{4}\right) d u \\ &=\int_{-1}^{1}\left(1-2 u^{2}+u^{4}\right) d u \\ &=\left.\left(u-\frac{2}{3} u^{3}+\frac{1}{5} u^{5}\right)\right|_{-1} ^{1} \\ &=\left(1-\frac{2}{3}+\frac{1}{5}\right)-\left(-1+\frac{2}{3}-\frac{1}{5}\right) \\ &=\frac{16}{15} , \end{aligned}$$ como vimos anteriormente.

Ejercicio$\PageIndex{20}$

Evaluar$\int_{0}^{\frac{\pi}{4}} \cos ^{5}(2 x) d x$.

Contestar

$\int_{0}^{\frac{\pi}{4}} \cos ^{5}(2 x) d x=\frac{4}{15}$

$$\begin{array}{l}{\sin ((a+b) x)=\sin (a x) \cos (b x)+\sin (b x) \cos (a x)} \\ {\sin ((a-b) x)=\sin (a x) \cos (b x)-\sin (b x) \cos (b x)} . \end{array}$$

Sumando estos juntos, tenemos $$2 \sin (a x) \cos (b x)=\sin ((a+b) x)+\sin ((a-b) x) ,$$ y así $$\sin (a x) \cos (b x)=\frac{1}{2}(\sin ((a+b) x)+\sin ((a-b) x)) .$$

Ejemplo$\PageIndex{14}$

Evaluar

$$\int_{0}^{\pi} \sin (2 x) \cos (3 x) d x ,$$ primero observamos que, usando$(2.6 .18)$ con$a=2$ y$b=3$, $$\sin (2 x) \cos (3 x)=\frac{1}{2}(\sin (5 x)+\sin (-x))=\frac{1}{2}(\sin (5 x)-\sin (x)) .$$ De ahí que $$\begin{aligned} \int_{0}^{\pi} \sin (2 x) \cos (3 x) d x &=\frac{1}{2} \int_{0}^{\pi} \sin (5 x) d x-\frac{1}{2} \int_{0}^{\pi} \sin (x) d x \\ &=-\left.\frac{1}{10} \cos (5 x)\right|_{0} ^{\pi}+\left.\frac{1}{2} \cos (x)\right|_{0} ^{\pi} \\ &=\left(\frac{1}{10}+\frac{1}{10}\right)+\left(-\frac{1}{2}-\frac{1}{2}\right) \\ &=-\frac{4}{5} . \end{aligned}$$ para integrales que involucren$\sin (a x) \sin (b x),$ comenzamos con las fórmulas de suma y resta del ángulo para coseno, $$\begin{array}{l}{\cos ((a+b) x)=\cos (a x) \cos (b x)-\sin (b x) \sin (a x)} \\ {\cos ((a-b) x)=\cos (a x) \cos (b x)+\sin (b x) \sin (b x)} . \end{array}$$ restando el primero de estos del segundo, tenemos $$2 \sin (a x) \sin (b x)=\cos ((a-b) x)-\cos ((a+b) x) ,$$ y así $$\sin (a x) \sin (b x)=\frac{1}{2}(\cos ((a-b) x)-\cos ((a+b) x)) .$$

Ejemplo$\PageIndex{15}$

Evaluar

$$\int_{0}^{\pi} \sin (3 x) \sin (5 x) d x ,$$ primero notamos que, usando$(2.6.22)$ con$a=3$ y$b=5$, $$\sin (3 x) \sin (5 x)=\frac{1}{2}(\cos (-2 x)-\cos (8 x))=\frac{1}{2}(\cos (2 x)-\cos (8 x)) .$$ Tenga en cuenta que tendríamos la misma identidad si hubiéramos elegido$a=5$ y$b=3 .$ Luego $$\begin{aligned} \int_{0}^{\pi} \sin (3 x) \sin (5 x) d x &=\frac{1}{2} \int_{0}^{\pi} \cos (2 x) d x-\frac{1}{2} \int_{0}^{\pi} \cos (8 x) d x \\ &=\left.\frac{1}{4} \sin (2 x)\right|_{0} ^{\pi}-\left.\frac{1}{16} \sin (8 x)\right|_{0} ^{\pi} \\ &=0 . \end{aligned}$$ Para integrales que involucren$\cos (a x) \cos (b x),$ agregamos$(2.6 .19)$$(2.6 .20)$ a para obtener $$2 \cos (a x) \cos (b x)=\cos ((a+b) x)+\cos ((a-b) x) ,$$ qué lleva a $$\cos (a x) \cos (b x)=\frac{1}{2}(\cos ((a+b) x)+\cos ((a-b) x)) .$$

Ejemplo$\PageIndex{16}$

Evaluar

$$\int_{0}^{\frac{\pi}{2}} \cos (3 x) \cos (5 x) d x ,$$ observamos que, usando$(2.6 .24)$ con$a=3$ y$b=5$, $$\cos (3 x) \cos (5 x)=\frac{1}{2}(\cos (8 x)+\cos (-2 x))=\frac{1}{2}(\cos (8 x)+\cos (2 x)) .$$ Por lo tanto $$\begin{aligned} \int_{0}^{\frac{\pi}{2}} \cos (3 x) \cos (5 x) d x &=\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \cos (8 x) d x+\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \cos (2 x) d x \\ &=\left.\frac{1}{16} \sin (8 x)\right|_{0} ^{\frac{\pi}{2}}-\left.\frac{1}{4} \sin (2 x)\right|_{0} ^{\frac{\pi}{2}} \\ &=0 . \end{aligned}$$

Ejercicio$\PageIndex{21}$

Evaluar$\int_{0}^{\frac{\pi}{2}} \sin (x) \cos (2 x) d x$.

Contestar

$\int_{0}^{\frac{\pi}{2}} \sin (2 x) \sin (x) d x=-\frac{1}{3}$

Ejercicio$\PageIndex{22}$

Evaluar$\int_{0}^{\frac{\pi}{2}} \sin (x) \sin (2 x) d x$.

Contestar

$\int_{0}^{\frac{\pi}{2}} \sin (x) \sin (2 x) d x=\frac{2}{3}$

Ejercicio$\PageIndex{23}$

Evaluar

$$\int_{0}^{\frac{\pi}{2}} \sin (3 x) \cos (3 x) d x .$$ Nota: Esto puede ser evaluado con una sustitución.

Contestar

$\int_{0}^{\frac{\pi}{2}} \sin (3 x) \cos (3 x) d x=\frac{1}{6}$

Ejercicio$\PageIndex{24}$

Evaluar$\int_{0}^{\frac{\pi}{2}} \cos (x) \cos (2 x) d x$.

Contestar

$\int_{0}^{\frac{\pi}{2}} \cos (x) \cos (2 x) d x=\frac{1}{3}$

Ejercicio$\PageIndex{25}$

Para cualquier número entero positivo$m$ y$n,$ mostrar que

$$\int_{0}^{2 \pi} \sin (m x) \cos (n x) d x=0 ,$$ $$\int_{0}^{2 \pi} \sin (m x) \sin (n x) d x=\left\{\begin{array}{ll}{0,} & {\text { if } m \neq n,} \\ {\pi} & {\text { if } m=n,}\end{array}\right.$$ y $$\int_{0}^{2 \pi} \cos (m x) \cos (n x) d x=\left\{\begin{array}{ll}{0,} & {\text { if } m \neq n,} \\ {\pi,} & {\text { if } m=n.}\end{array}\right.$$

2.6.4 Cambio de Variable Revisitada

Supongamos que$f$ es una función continua en el intervalo$[a, b]$ y$\varphi$ es una función creciente definida en un intervalo$[c, d]$ con$\varphi(c)=a$ y$\varphi(d)=b,$ o una función decreciente definida en$[c, d]$ con$\varphi(c)=b$ y$\varphi(d)=a .$ Entonces,$(2.6 .5),$ cambiando la notación según sea necesario,

$$\int_{a}^{b} f(x) d x=\int_{c}^{d} f(\varphi(z)) \varphi^{\prime}(z) d z .$$ Anteriormente solíamos$(2.6 .25)$ simplificar las integrales en la forma del lado derecho; en esta sección veremos algunos ejemplos que simplifican en la otra dirección.

Ejemplo$\PageIndex{17}$

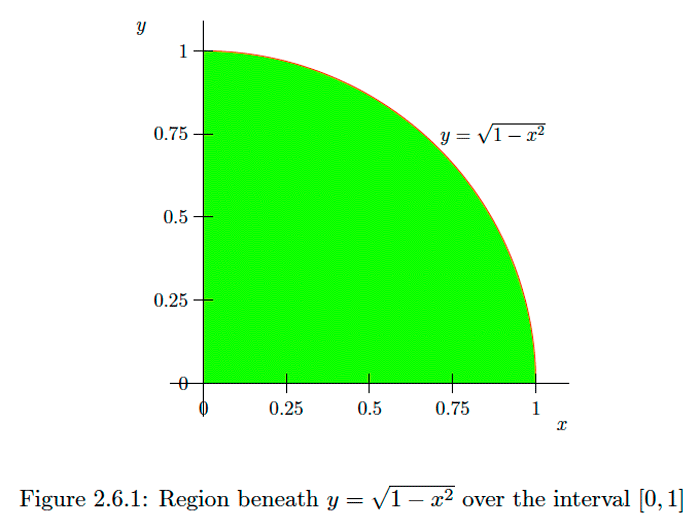
Dado que la gráfica de$y=\sqrt{1-x^{2}}$ for$0 \leq x \leq 1$ es una cuarta parte del círculo$\left.x^{2}+y^{2}=1 \text { (see Figure } 2.6 .1\right),$ sabemos que

$$\int_{0}^{1} \sqrt{1-x^{2}} d x=\frac{\pi}{4} .$$ Ahora veremos cómo utilizar un cambio de variable para evaluar esta integral utilizando el teorema fundamental. La idea es hacer uso de la identidad trigonométrica Es$1-\sin ^{2}(z)=\cos ^{2}(z) .$ decir, supongamos que dejamos$x=\sin (z)$ para$0 \leq z \leq \frac{\pi}{2} .$ Entonces $$\sqrt{1-x^{2}}=\sqrt{1-\sin ^{2}(z)}=\sqrt{\cos ^{2}(z)}=|\cos (z)|=\cos (z) ,$$ donde sigue la igualdad final ya que$\cos (z) \geq 0$ por$0 \leq z \leq \frac{\pi}{2} .$ Ahora $$d x=\cos (z) d z ,$$

así que tenemos

$$\begin{aligned} \int_{0}^{1} \sqrt{1-x^{2}} d x &=\int_{0}^{\frac{\pi}{2}} \cos (z) \cos (z) d z \\ &=\int_{0}^{\frac{\pi}{2}} \cos ^{2}(z) d z \\ &=\frac{1}{2} \int_{0}^{\frac{\pi}{2}}(1+\cos (2 z)) d z \\ &=\left.\frac{1}{2} z\right|_{0} ^{\frac{\pi}{2}}+\left.\frac{1}{4} \sin (2 z)\right|_{0} ^{\frac{\pi}{2}} \\ &=\frac{\pi}{4} , \end{aligned}$$ como esperábamos.

Ejemplo$\PageIndex{18}$

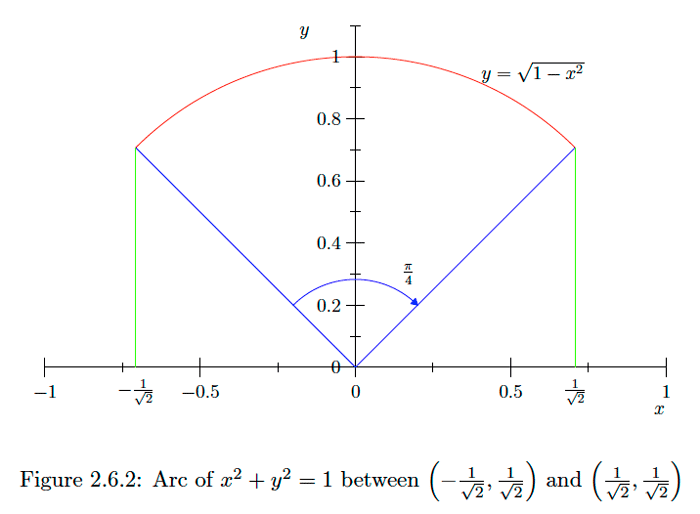
Dejar$C$ ser el círculo con ecuación$x^{2}+y^{2}=1$ y dejar que$L$ sea la longitud del arco más corto de$C$ entre$\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$ y$\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$ (ver Figura$2.6 .2) .$ ya que la circunferencia de$C$ es$2 \pi$ y este arco es un cuarto de la circunferencia de$C,$ debemos tener Ahora$L=\frac{\pi}{2} .$ vamos a demostrar que esto concuerda con$(2.5 .28),$ la fórmula que derivamos para calcular la longitud del arco. Ahora$y=\sqrt{1-x^{2}},$ así

$$\frac{d y}{d x}=\frac{1}{2}\left(1-x^{2}\right)^{-\frac{1}{2}}(-2 x)=-\frac{x}{\sqrt{1-x^{2}}} .$$ De $$\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=\sqrt{1+\frac{x^{2}}{1-x^{2}}}=\sqrt{\frac{1-x^{2}+x^{2}}{1-x^{2}}}=\frac{1}{\sqrt{1-x^{2}}} .$$ ahí ahí, por$(2.5 .28)$, $$L=\int_{-\frac{1}{\sqrt{2}}}^{\frac{1}{\sqrt{2}}} \frac{1}{\sqrt{1-x^{2}}} d x .$$ Si dejamos $$\begin{aligned} x &=\sin (z) \\ d x &=\cos (z) d z, \end{aligned}$$ entonces $$\begin{aligned} L &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{1}{\sqrt{1-\sin ^{2}(z)}} \cos (z) d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{\cos (z)}{\sqrt{\cos ^{2}(z)}} d z \\ &=\int_{-\frac{\pi}{4}}^{-\frac{\pi}{4}} \frac{\cos (z)}{\cos (z)} d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d z \\ &=\frac{\pi}{2} . \end{aligned}$$

Ejercicio$\PageIndex{26}$

Utilizar el cambio de variable$x=2 \sin (z)$ para evaluar

$$\int_{-2}^{2} \sqrt{4-x^{2}} d x ,$$

Contestar

$\int_{-2}^{2} \sqrt{4-x^{2}} d x=2 \pi$

Ejercicio$\PageIndex{27}$

Evaluar$\int_{-2}^{1} \frac{2}{\sqrt{16-x^{2}}} d x$.

Contestar

$\int_{-2}^{2} \frac{2}{\sqrt{16-x^{2}}} d x=\frac{\pi}{6}$

Ejemplo$\PageIndex{19}$

En el Ejemplo 2.5.8 vimos que la longitud$L$ del arco de la parábola$y=x^{2}$ sobre el intervalo$[0,1]$ es

$$L=\int_{0}^{1} \sqrt{1+4 x^{2}} d x .$$ No obstante, en ese momento no contábamos con los medios para evaluar esta integral. Ahora tenemos la mayoría, aunque no todas, de las herramientas necesarias. Para comenzar, primero haremos el cambio de variable $$\begin{aligned} u &=2 x \\ d u &=2 d x, \end{aligned}$$ que nos da $$L=\frac{1}{2} \int_{0}^{2} \sqrt{1+u^{2}} d u .$$ A continuación, recordamos la identidad trigonométrica $$1+\tan ^{2}(t)=\sec ^{2}(t)$$ (una consecuencia de dividir cada término de la identidad$\cos ^{2}(t)+\sin ^{2}(t)=1$ por la$\left.\cos ^{2}(t)\right),$ cual es un indicio de que el cambio de variable $$\begin{aligned} x &=\tan (z) \\ d x &=\sec ^{2}(z) \end{aligned}$$ podría ser de utilidad. Si dejamos$\alpha$ ser el ángulo para el que$\tan (\alpha)=2,$ con$0<\alpha<\frac{\pi}{2}$, y señalar que$\tan (0)=0$ y $$\sqrt{1+\tan ^{2}(z)}=\sqrt{\sec ^{2}(z)}=|\sec (z)|=\sec (z)$$ (tenga en cuenta que$\left.\sec (z)>0 \text { since } 0 \leq z \leq \frac{\pi}{2}\right),$ entonces $$L=\frac{1}{2} \int_{0}^{\alpha} \sec (z) \sec ^{2}(z) d z=\frac{1}{2} \int_{0}^{\alpha} \sec ^{3}(z) d z .$$ podemos reducir la integral a la derecha usando una integración por partes: Dejando $$\begin{aligned} u &=\sec (z) d z & & d v=\sec ^{2}(z) d x \\ d u &=\sec (z) \tan (z) d z & & v=\tan (z) ,\end{aligned}$$ que tengamos $$\begin{aligned} \int_{0}^{\alpha} \sec ^{3}(z) d z &=\left.\sec (z) \tan (z)\right|_{0} ^{\alpha}-\int_{0}^{\alpha} \sec (z) \tan ^{2}(z) d z \\ &=\sec (\alpha) \tan (\alpha)-\int_{0}^{\alpha} \sec (z)\left(\sec ^{2}(z)-1\right) d z \\ &=2 \sqrt{5}-\int_{0}^{\alpha} \sec ^{3}(z) d z+\int_{0}^{\alpha} \sec (z) d z ,\end{aligned}$$ donde hemos usado el hecho de que $\tan (\alpha)=2$y$1+\tan ^{2}(\alpha)=\sec ^{2}(z)$ para encontrar$\sec (\alpha)=\sqrt{5} .$ eso Ahora se deduce eso $$2 \int_{0}^{\alpha} \sec ^{3}(z) d z=2 \sqrt{5}+\int_{0}^{\alpha} \sec (z) d z ,$$ y así $$\int_{0}^{\alpha} \sec ^{3}(z) d z=\sqrt{5}+\frac{1}{2} \int_{0}^{\alpha} \sec (z) d z .$$ De ahí $$L=\frac{\sqrt{5}}{2}+\frac{1}{4} \int_{0}^{\alpha} \sec (z) d z .$$ Para esta integral reducida, notamos que $$\int_{0}^{\alpha} \sec (z) d z=\int_{0}^{\alpha} \sec (z) \frac{\sec (z)+\tan (z)}{\sec (z)+\tan (z)} d z=\int_{0}^{\alpha} \frac{\sec ^{2}(z)+\sec (z) \tan (z)}{\sec (z)+\tan (z)} d z ,$$ y así el cambio de variable nos $$\begin{aligned} w &=\sec (z)+\tan (z) \\ d w &=\left(\sec (z) \tan (z)+\sec ^{2}(z)\right) d z \end{aligned}$$ da $$\int_{0}^{\alpha} \sec (z) d z=\int_{1}^{2+\sqrt{5}} \frac{1}{w} d w .$$ Así ahora tenemos $$L=\frac{\sqrt{5}}{2}+\frac{1}{4} \int_{1}^{2+\sqrt{5}} \frac{1}{w} d w .$$ Aunque muy simplificado de la integral con la que empezamos, sin embargo no podemos evaluar la integral restante con nuestras herramientas actuales. En efecto, podemos usar el teorema fundamental del cálculo para evaluar, para cualquier número racional$n,$ cualquier integral definida que implique$w^{n},$ excepto en el mismo caso que estamos enfrentando ahora, es decir, cuándo$n=-1 .$ llenaremos este vacío en la siguiente sección, y terminaremos este ejemplo en ese momento (ver Ejemplo$2.7 .9) .$

Ejemplo$\PageIndex{20}$

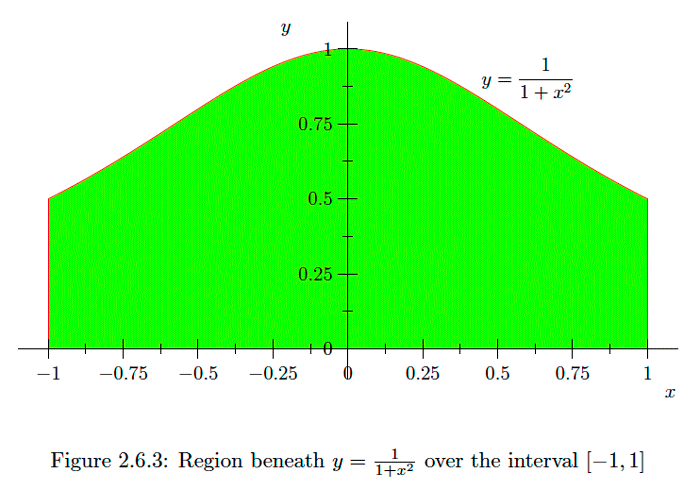
Para un ejemplo más sencillo del cambio de variable utilizado en el ejemplo anterior, considere la integral

$$\int_{-1}^{1} \frac{1}{1+x^{2}} d x ,$$ el área bajo la curva $$y=\frac{1}{1+x^{2}}$$ sobre el intervalo$[-1,1] \text { (see Figure } 2.6 .3) .$ Si dejamos $$\begin{aligned} x &=\tan (z) \\ d x &=\sec ^{2}(z) d z, \end{aligned}$$

y tenga en cuenta que$\tan \left(-\frac{\pi}{4}\right)=-1$ y$\tan \left(\frac{\pi}{4}\right)=1,$ luego

$$\begin{aligned} \int_{-1}^{1} \frac{1}{1+x^{2}} d x &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{1}{1+\tan ^{2}(z)} \sec ^{2}(z) d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{\sec ^{2}(z)}{\sec ^{2}(z)} d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d z \\ &=\frac{\pi}{2}. \end{aligned}$$ Deberías comparar esto con la simple aproximación que vimos en Ejemplo$2.3 .1 .$

Ejercicio$\PageIndex{28}$

Evaluar$\int_{-3}^{3} \frac{6}{9+x^{2}} d x$.

Contestar

$\int_{-3}^{3} \frac{6}{9+x^{2}} d x=\pi$

Ejercicio$\PageIndex{29}$

Evaluar$\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{1}{1+4 x^{2}} d x$.

Contestar

$\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{1}{1+4 x^{2}} d x=\frac{\pi}{4}$

Ejercicio$\PageIndex{30}$

Mostrar que para cualquier entero positivo$n>2$,

$$\int \sec ^{n}(x) d x=\frac{1}{n-1} \sec ^{n-2}(x) \tan (x)+\frac{n-2}{n-1} \int \sec ^{n-2}(x) d x.$$