3.1: Pruebas directas

Última actualización
Guardar como PDF

Page ID: 116091

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Vista previa Actividad 1 (Definición de Divides, Divisor, Múltiple)
En la Sección 1.2, estudiamos los conceptos de enteros pares e enteros impares. La definición de un entero par era una formalización de nuestro concepto de un entero par como siendo uno esto es “divisible por 2”, o un “múltiplo de 2”. También podríamos decir que si “2 divide un entero”, entonces ese entero es un entero par. Ahora vamos a extender esta idea a enteros distintos de 2. A continuación se presenta una definición formal de lo que significa decir que un entero distinto de cero$m$ divide un entero$n$.

Definición

Un entero distinto de cero$m$ divide un entero$n$ siempre que haya un entero$q$ tal que$n = m \cdot q$. También decimos que$m$ es un divisor de$n$,$m$ es un factor de$n$, y$n$ es un múltiplo de$m$. El entero 0 no es un divisor de ningún entero. Si$a$ y$b$ son enteros y$a \ne 0$, frecuentemente usamos la notación$a | b$ como una taquigrafía para “$a$divide”$b$.

Una Nota sobre Notación: Tenga cuidado con la notación$a | b$. Esto no representa el número racional$\dfrac{a}{b}$. La notación$a | b$ representa una relación entre los enteros$a$ y$b$ y es simplemente una taquigrafía para “$a$divide”$b$.

Una Nota sobre Definiciones: Técnicamente, una definición en matemáticas casi siempre debe escribirse usando “si y solo si”. No está claro por qué, pero la convención en matemáticas es sustituir la frase “si y sólo si” por “si” o un equivalente. Quizás esto sea un poco de pereza o la frase “si y solo si” puede ser un poco engorrosa. En este texto, a menudo usaremos la frase “siempre que” en su lugar.

La definición de “divide” se puede escribir en forma simbólica utilizando cuantificadores apropiados de la siguiente manera: Un entero distinto de cero$m$ divide un entero$n$ siempre que$(\exists q \in \mathbb{Z})(n = m \cdot q)$.

Utilice la definición de divisiones para explicar por qué 4 divide 32 y para explicar por qué 8 divide -96.
Dé varios ejemplos de dos enteros donde el primer entero no divide al segundo entero.
De acuerdo con la definición de “divide”, ¿el entero 10 divide al entero 0? Es decir, ¿es 10 un divisor de 0? Explique.
Usa la definición de “divide” para completar la siguiente oración en forma simbólica: “El entero distinto de cero$m$ no divide el entero$n$ significa que...”
Usa la definición de “divide” para completar la siguiente oración sin usar los símbolos para los cuantificadores: “El entero distinto de cero$m$ no divide el entero$n$....”
Dar tres ejemplos diferentes de tres enteros donde el primer entero divide el segundo entero y el segundo entero divide el tercer entero.

Como hemos visto en la Sección 1.2, se utiliza frecuentemente una definición a la hora de construir y escribir pruebas matemáticas. Considere la siguiente conjetura:

Conjetura: Dejar$a$,$b$ y$c$ ser enteros con$a \ne 0$ y$b \ne 0$. Si$a$ divide$b$ y$b$ divide$c$, entonces$a$ divide$c$.
Explica por qué los ejemplos que generaste en la parte (6) proporcionan evidencia de que esta conjetura es cierta.
En la Sección 1.2, también aprendimos a usar una mesa de know show para ayudar a organizar nuestros pensamientos al intentar construir una prueba de una declaración. Si es necesario, revisar el material apropiado en la Sección 1.2.
Declarar precisamente lo que supondríamos si estuviéramos tratando de escribir una prueba de la conjetura anterior.
Usa la definición de “divide” para sacar algunas conclusiones basadas en tus suposiciones en parte (8).
Declarar precisamente lo que estaríamos tratando de probar si estuviéramos tratando de escribir una prueba de la conjetura.
Usa la definición de divisiones para escribir una respuesta a la pregunta, “¿Cómo podemos probar lo que dijimos en la parte (10)?

Vista previa Actividad 2 (Calendarios y Relojes)
Esta actividad de vista previa está destinada a ayudar a comprender el concepto de congruencia, que se estudiará al final de esta sección.

Supongamos que actualmente es martes. a) ¿Qué día serán dentro de 3 días?
b) ¿Qué día serán dentro de 10 días?
c) ¿Qué día serán 17 días a partir de ahora? ¿Qué día serán dentro de 24 días?
(d) Encontrar varios otros números naturales de$x$ tal manera que será viernes$x$ días a partir de ahora.
(e) Crear una lista (en orden creciente) de los números 3; 10; 17; 24, y los números que generaste en la Parte (1d). Elige dos números cualesquiera de esta lista y resta uno del otro. Repite esto varias veces.
f) ¿Qué tienen en común los números que obtuvo en la Parte (1e)?
Supongamos que estamos usando un reloj de doce horas sin distinción entre A.M. y P.M. Además, supongamos que la hora actual es de las 5:00. a) ¿A qué hora serán dentro de 4 horas?
b) ¿A qué hora serán dentro de 16 horas? ¿A qué hora serán 28 horas a partir de ahora?
(c) Encontrar varios otros números naturales de$x$ tal manera que serán las 9:00$x$ horas a partir de ahora.
(d) Crear una lista (en orden creciente) de los números 4; 16; 28, y los números que generaste en la Parte (2c). Elige dos números cualesquiera de esta lista y resta uno del otro. Repite esto varias veces.
e) ¿Qué tienen en común los números que obtuvo en la Parte (2d)?
Esta es una continuación de la Parte (1). Supongamos que actualmente es martes.

a) ¿Qué día fue hace 4 días?
b) ¿Qué día fue hace 11 días? ¿Qué día fue hace 18 días?
(c) Encontrar varios otros números naturales de$x$ tal manera que fue viernes hace$x$ días.
(d) Crear una lista (en orden creciente) consistente en los números18; 11; 4, los opuestos de los números que generaste en la Parte (3c) y los números positivos en la lista de la Parte (1e). Elige dos números cualesquiera de esta lista y resta uno del otro. Repite esto varias veces.
e) ¿Qué tienen en común los números que obtuvo en la Parte (3d)?

Algo de Terminología Matemática

En la Sección 1.2, presentamos la idea de una prueba directa. Desde entonces, hemos utilizado alguna terminología común en matemáticas sin mucha explicación. Antes de continuar, discutiremos algunos términos matemáticos de uso frecuente.

Una prueba en matemáticas es un argumento convincente de que alguna afirmación matemática es cierta. Una prueba debe contener suficiente detalle matemático para ser convincente a la (s) persona (s) a quien se dirige la prueba. En esencia, una prueba es un argumento que comunica una verdad matemática a otra persona (que tiene los antecedentes matemáticos apropiados). Una prueba debe utilizar un razonamiento correcto y lógico y basarse en resultados previamente establecidos. Estos resultados previos pueden ser axiomas, definiciones o teoremas previamente probados. Estos términos se discuten a continuación.

Sorprendente para algunos es el hecho de que en matemáticas, siempre hay términos indefinidos. Esto es porque si intentáramos definir todo, terminaríamos yendo en círculos. En pocas palabras, debemos comenzar por alguna parte. Por ejemplo, en geometría euclidiana, los términos “punto”, “línea” y “contiene” son términos indefinidos. En este texto, estamos utilizando nuestros sistemas numéricos como los números naturales y los enteros como términos indefinidos. A menudo asumimos que estos objetos indefinidos satisfacen ciertas propiedades. Estas relaciones asumidas son aceptadas como verdaderas sin pruebas y se llaman axiomas (o postulados). Un axioma es una afirmación matemática que se acepta sin pruebas. La geometría euclidiana comienza con términos indefinidos y un conjunto de postulados y axiomas. Por ejemplo, la siguiente declaración es un axioma de geometría euclidiana:

Dados dos puntos distintos, hay exactamente una línea que contiene estos dos puntos.

Las propiedades de cierre de los sistemas numéricos discutidos en la Sección 1.1 y las propiedades de los sistemas numéricos en la Tabla 1.2 de la página 18 se están utilizando como axiomas en este texto.

Una definición es simplemente un acuerdo en cuanto al significado de un término en particular. Por ejemplo, en este texto, hemos definido los términos “entero par” y “entero impar”. Las definiciones no se hacen al azar, sino que generalmente se hace una definición porque se observa que una determinada propiedad ocurre con frecuencia. Como resultado, se vuelve conveniente darle a esta propiedad su propio nombre especial. Las definiciones que se han hecho pueden ser utilizadas en el desarrollo de pruebas matemáticas. De hecho, la mayoría de las pruebas requieren el uso de algunas definiciones.

Al tratar con declaraciones matemáticas, frecuentemente usamos los términos “conjetura”, “teorema”, “proposición”, “lema” y “corolario”. Una conjetura es una afirmación que creemos que es plausible. Es decir, pensamos que es cierto, pero aún no hemos desarrollado una prueba de que sea verdad. Un teorema es una afirmación matemática de la que tenemos una prueba. Un término que a menudo se considera sinónimo de “teorema” es la proposición.

A menudo la prueba de un teorema puede ser bastante larga. En este caso, muchas veces es más fácil comunicar la prueba en “piezas” más pequeñas. Estas piezas de soporte a menudo se llaman lemmas. Un lema es una verdadera afirmación matemática que se demostró principalmente para ayudar en la prueba de algún teorema. Una vez que se ha probado un teorema dado, suele darse el caso de que otras proposiciones se derivan inmediatamente del hecho de que el teorema es cierto. A estos se les llama corolarios del teorema. El término corolario se utiliza para referirse a un teorema que es fácilmente probado una vez que se ha probado algún otro teorema.

Construyendo pruebas matemáticas

Para crear una prueba de un teorema, debemos utilizar el razonamiento lógico correcto y las afirmaciones matemáticas que ya aceptamos como verdaderas. Estas declaraciones incluyen axiomas, definiciones, teoremas, lemmas y corolarios.

En la Sección 1.2, introdujimos el uso de una mesa de know show para ayudarnos a organizar nuestro trabajo cuando intentamos probar una declaración. También introdujimos algunas pautas para escribir pruebas matemáticas una vez que hemos creado la prueba. Estos lineamientos deben ser revisados antes de continuar.

Por favor, recuerde que cuando iniciamos el proceso de redacción de una prueba, esencialmente estamos “reportando la noticia”. Es decir, ya hemos descubierto la prueba, y ahora tenemos que denunciarla. Este reportaje a menudo no describe el proceso de descubrimiento de la noticia (la parte investigativa del proceso).

Muy a menudo, el primer paso es desarrollar una conjetura. Esto a menudo se hace después de trabajar dentro de ciertos objetos durante algún tiempo. Esto es lo que hicimos en Preview Activity$\PageIndex{1}$ cuando usamos ejemplos para proporcionar evidencia de que la siguiente conjetura es cierta:

Conjetura: Dejar$a$,$b$ y$c$ ser enteros con$a \ne 0$ y$b \ne 0$. Si$a$ divide$b$ y$b$ divide$c$, entonces se$a$ desvía$c$.

Antes de intentar probar una conjetura, debemos asegurarnos de haber explorado algunos ejemplos. Esto simplemente significa construir algunos ejemplos específicos donde los enteros a, b y c satisfacen la hipótesis de la conjetura para ver si también satisfacen la conclusión. Hicimos esto por esta conjetura en Actividad Previa$\PageIndex{1}$.

Ahora iniciaremos una tabla de saber-show para esta conjetura.

Paso	Conoce	Razón
$P$	$a$,$b$,$c \in \mathbb{Z}$,$a \ne 0$,$b \ne 0$,$a \| b$ y$b \| c$	Hipótesis
$P$1
...	...	...
$Q$1
$Q$	$a \| c$
Paso	Mostrar	Razón

La pregunta atrasada que hacemos es: “¿Cómo podemos probar que$a$ divide$c$?” Una respuesta es usar la definición y mostrar que existe un entero$q$ tal que$c = a \cdot q$. Este podría ser el paso$Q$ 1 en la tabla de conocimientos.

Ahora tenemos que probar que$q$ existe cierto número entero, así que hacemos la pregunta: “¿Cómo demostramos que este entero existe?” Cuando estamos en tal etapa del proceso atrasado de una prueba, solemos recurrir a lo que se sabe para probar que el objeto existe o para encontrar o construir el objeto que estamos tratando de demostrar que existe. A menudo decimos que tratamos de “construir” el objeto o al menos demostrar que existe a partir de la información conocida. Entonces en este punto, vamos a la parte delantera de la prueba para tratar de probar que existe un entero$q$ tal que$c = a \cdot q$.

La pregunta hacia adelante que nos hacemos es: “¿Qué podemos concluir de los hechos que$a | b$ y$b | c$?” Nuevamente, usando la definición, sabemos que existen enteros$s$ y$t$ tal que$b = a \cdot s$ y$c = b \cdot t$. Este podría ser el paso$P$ 1 en la tabla de conocimientos.

La clave ahora es determinar cómo llegar del$P$ 1 al$Q$ 1. Es decir, ¿podemos usar las conclusiones de que los enteros$s$ y$t$ existen para probar que el entero$q$ (desde el proceso hacia atrás) existe. Usando la ecuación$b = a \cdot s$, podemos sustituir$a \cdot s$$b$ en la segunda ecuación,$c = b \cdot t$. Esto da

$c = b \cdot t$
$= (a \cdot s) \cdot t$
$= a(s \cdot t)$.

El último paso utilizó la propiedad asociativa de la multiplicación. (Véase el Cuadro 1.2 en la página 18.) Esto demuestra que$c$ es igual a$a$ veces algún entero. (Esto se debe a que$s \cdot t$ es un entero por la propiedad closure para enteros.) Entonces aunque no usamos la carta$q$, hemos llegado al paso$Q$ 1. A continuación se muestra la tabla de conocimientos completos.

Paso	Conoce	Razón
$P$	$a$,$b$,$c \in \mathbb{Z}$,$a \ne 0$,$b \ne 0$,$a \| b$ y$b \| c$	Hipótesis
$P$1	$(\exists s \in \mathbb{Z})(b = a \cdot s)$ $(\exists t \in \mathbb{Z})(c = b \cdot t)$	Definición de “Divide”
$P$2	$c = (a \cdot s) \cdot t$	Sustitución por$b$
$P$3	$c = a \cdot (s \cdot t$)	Propiedad asociativa de la multiplicación
$Q$1	$(\exists q \in \mathbb{Z})(c = a \cdot q)$	Paso$P$ 3 y las propiedades de cierre de los enteros
$Q$	$a \| c$	Definición de “divide”

Observe las similitudes entre lo que hicimos para esta prueba y muchas de las pruebas sobre enteros pares e impares que construimos en la Sección 1.2. Cuando tratamos de demostrar que existe cierto objeto, a menudo usamos lo que se llama el método de construcción como prueba. La aparición de un cuantificador existencial en la parte show (o hacia atrás) de la prueba suele ser el indicador para ir a lo que se conoce para probar que el objeto existe.

Ahora podemos reportar la noticia escribiendo una prueba formal.

Teorema 3.1

Dejar$a$,$b$ y$c$ ser enteros con$a \ne 0$ y$b \ne 0$. Si$a$ divide$b$ y$b$ divide$c$, entonces$a$ divide$c$.

Prueba

Suponemos que$a$,$b$, y$c$ son enteros con$a \ne 0$ y$b \ne 0$. Asumimos además que$a$ divide$b$ y eso$b$ divide$c$. Vamos a probar que$a$ divide$c$.

Ya que$a$ divide$b$ y$b$ divide$c$, existe un número entero$s$ y$t$ tal que

\[b = a \cdot s, and\]

\[c = b \cdot t\]

Ahora podemos sustituir la expresión$b$ de la ecuación (1) en la ecuación (2). Esto da

$c = (a \cdot s) \cdot t$.

Usando la propiedad associate para la multiplicación, podemos reorganizar el lado derecho de la última ecuación para obtener

$c = a \cdot (s \cdot t)$.

Porque tanto s como t son enteros, y como los enteros están cerrados bajo multiplicación, eso lo sabemos$s \cdot t \in \mathbb{Z}$. Por lo tanto, la ecuación anterior prueba que$a$ divide$c$. En consecuencia, hemos demostrado que siempre$a$$b$,, y$c$ son enteros con$a \ne 0$ y$b \ne 0$ tal que$a$$b$ divide$b$ y divide$c$, luego$a$ divide$c$.

Pautas de escritura para números de ecuaciones

Escribimos la prueba para el Teorema 3.1 de acuerdo con los lineamientos introducidos en la Sección 1.2, pero un nuevo elemento que apareció en esta prueba fue el uso de números de ecuaciones. A continuación se presentan algunas pautas que se pueden utilizar para los números de ecuación.

Si es necesario hacer referencia a una ecuación más adelante en una prueba, esa ecuación debe ser centrada y mostrada. Entonces se le debe dar un número. El número de la ecuación debe escribirse entre paréntesis en la misma línea que la ecuación en el margen derecho como se muestra en el siguiente ejemplo.

Dado que$x$ es un entero impar, existe un entero$n$ tal que

\[x = 2n + 1\].

Posteriormente en la prueba, puede haber una línea como

Entonces, usando el resultado en la ecuación (1), obtenemos..

Observe que no numeramos todas las ecuaciones en el Teorema 3.1. Solo debemos numerar aquellas ecuaciones a las que nos referiremos más adelante en la prueba, y solo debemos numerar las ecuaciones cuando sea necesario. Por ejemplo, en lugar de numerar una ecuación, a menudo es mejor usar una frase como, “la ecuación anterior lo demuestra.” o “podemos reorganizar los términos en el lado derecho de la ecuación anterior”. Además, tenga en cuenta que la palabra “ecuación” no se pone en mayúscula cuando nos estamos refiriendo a una ecuación por número. Si bien puede ser apropiado usar una “E” mayúscula, la convención habitual en matemáticas no es capitalizar.

Comprobación de progreso 3.2 (Una propiedad de divisores)

Dar por lo menos cuatro ejemplos diferentes de enteros$a$$b$,, y$c$ con$a \ne 0$ tal que$a$ divide$b$ y$a$ divide$c$.
Para cada ejemplo en la Parte (1), calcule la suma$b + c$. ¿El entero$a$ divide la suma$b + c$?
Construya una tabla de know show para la siguiente proposición: Para todos los enteros$a$$a \ne 0$,, y$c$ con, si$a$$a$ divide$b$ y divide$c$, entonces a divide$b + c$.$b$

Contestar: Agrega textos aquí. No elimine primero este texto.

Uso de contraejemplos

En la Sección 1.2 y hasta ahora en esta sección, nuestro enfoque ha estado en probar declaraciones que involucren cuantificadores universales. No obstante, otra habilidad importante para los matemáticos es poder reconocer cuando una declaración es falsa y luego poder demostrar que es falsa. Por ejemplo, supongamos que queremos saber si la siguiente proposición es verdadera o falsa.

Para cada entero$n$, si 5 divide$n^2 - 1$, entonces 5 divide$n - 1$.

Supongamos que empezamos a intentar probar esta proposición. En el proceso hacia atrás, diríamos que para probar que 5 divide$n - 1$, podemos demostrar que existe un entero$k$ tal que

$Q_1$:$n - 1 = 5k$ o$n = 5k + 1$.

Para el proceso hacia adelante, podríamos decir que desde 5 divide (n^2 - 1), sabemos que existe un interger$m$ tal que

$P_1$:$n^2 -1 = 5m$ o$n^2 = 5m + 1$.

El problema es que no hay una manera sencilla de usar$P_1$ para probar$Q_1$. En este punto, sería una buena idea probar algunos ejemplos para$n$ y tratar de encontrar situaciones en las que la hipótesis de la proposición sea cierta. (De hecho, esto debió haberse hecho antes de que empezáramos a intentar probar la proposición). La siguiente tabla resume los resultados de algunas de estas exploraciones con valores para$n$.

$n$	$n^2 -1$	Hace 5 divide ($n^2 - 1$)	$n - 1$	Hace 5 divide ($n - 1$)
\ (n\) ">1	\ (n^2 -1\) ">0	\ (n^2 - 1\)) ">sí	\ (n - 1\) ">0	\ (n - 1\)) ">sí
\ (n\) ">2	\ (n^2 -1\) ">3	\ (n^2 - 1\)) ">no	\ (n - 1\) ">1	\ (n - 1\)) ">no
\ (n\) ">3	\ (n^2 -1\) ">8	\ (n^2 - 1\)) ">no	\ (n - 1\) ">2	\ (n - 1\)) ">no
\ (n\) ">4	\ (n^2 -1\) ">15	\ (n^2 - 1\)) ">sí	\ (n - 1\) ">3	\ (n - 1\)) ">no

Podemos dejar de explorar ejemplos ahora ya que la última fila de la tabla proporciona un ejemplo donde la hipótesis es verdadera y la conclusión es falsa. Recordemos de la Sección 2.4 (ver página 69) que un contraejemplo para una declaración de la forma$\forall x \in U)(P(x))$ es un elemento a en el conjunto universal para el cual$P(a)$ es falso. Así que en realidad hemos demostrado que la negación de la proposición es cierta.

Cuando se usa un contraejemplo para probar que una declaración es falsa, no utilizamos el término “prueba” ya que nos reservamos una prueba para probar que una proposición es verdadera. Podríamos resumir nuestro trabajo de la siguiente manera:

Conjetura. Por cada entero$n$, si 5 divide ($n^2$- 1), entonces 5 divide ($n$- 1).

El entero$n$ = 4 es un contraejemplo que demuestra que esta conjetura es falsa. Observe que cuando$n$ = 4,$n^2$ - 1 = 15 y 5 divide 15. De ahí que la hipótesis de la conjetura sea cierta en este caso. Además,$n$ - 1 = 3 y 5 no divide 3 y así la conclusión de la conjetura es falsa en este caso. Dado que este es un ejemplo donde la hipótesis es verdadera y la conclusión es falsa, la conjetura es falsa.

Como regla general, cada vez que estamos tratando de decidir si una proposición es verdadera o falsa, es una buena idea probar primero algunos ejemplos. Los ejemplos que se escojan deben ser aquellos en los que la hipótesis de la proposición sea cierta. Si uno de estos ejemplos hace falsa la conclusión, entonces hemos encontrado un contraejemplo y sabemos que la proposición es falsa. Si todos los ejemplos producen una conclusión verdadera, entonces tenemos evidencia de que la proposición es verdadera y podemos intentar escribir una prueba.

Comprobación de progreso 3.3: Uso de un contraejemplo

Use un contraejemplo para probar que la siguiente declaración es falsa.

Para todos los enteros$a$ y$b$, si 5 divide$a$ o 5 divide$b$, entonces 5 divide (5$a$ +$b$).

Contestar: Agrega textos aquí. No elimine primero este texto.

Congruencia

Lo que los matemáticos llaman congruencia es un concepto utilizado para describir ciclos en el mundo de los enteros. Por ejemplo, el día de la semana es un fenómeno cíclico en que el día de la semana se repite cada siete días. La hora del día es un fenómeno cíclico porque se repite cada 12 horas si usamos un reloj de 12 horas o cada 24 horas si usamos un reloj de 24 horas. Exploramos estos dos fenómenos cíclicos en Actividad Previa$\PageIndex{2}$.

Similar a lo que vimos en Actividad Previa$\PageIndex{2}$, si actualmente es lunes, entonces será miércoles 2 días a partir de ahora, 9 días a partir de ahora, 16 días a partir de ahora, 23 días a partir de ahora, y así sucesivamente. Además, fue miércoles hace 5 días, hace 12 días, 19 días, y así sucesivamente. Usando números negativos para el tiempo en el pasado, generamos la siguiente lista de números:

..., -19, -12, -5, 2, 9, 16, 23,...

Observe que si restamos algún número de la lista anterior de cualquier otro número de esa lista, obtendremos un múltiplo de 7. Por ejemplo,

Ejemplo:

16 - 2 = 14 = 7$\cdot$ 2

(-5) - (9) = -14 = 7$\cdot$ (-2)

16 - (-12) = 28 = 7$\cdot$ 4.

Usando el concepto de congruencia, diríamos que todos los números en esta lista son congruentes módulo 7, pero primero tenemos que definir cuando dos números son congruentes módulo algún número natural$n$.

Definición

Vamos$n \in \mathbb{N}$. Si$a$ y$b$ son enteros, entonces decimos que $a$es congruente con$b$ modulo$n$ siempre que se$n$ divida$a - b$. Una notación estándar para esto es$a \equiv b$ (mod$n$). Esto se lee como “$a$es congruente con$b$ módulo$n$” o “$a$es congruente con$b$ mod”$n$.

Observe que podemos usar la definición de divide para decir que$n$ divide$a - b$ si y sólo si existe un entero$k$ tal que$a - b = nk$. Así podemos escribir

$a \equiv b$(mod$n$) significa$(\exists k \in \mathbb{Z})(a - b = nk)$, o
$a \equiv b$ (mod$n$) significa$(\exists k \in \mathbb{Z})(a = b + nk)$.

Esto quiere decir que para encontrar enteros que sean congruentes al$b$ módulo$n$, solo necesitamos agregar múltiplos de$n$ to$b$. Por ejemplo, para encontrar enteros que son congruentes a 2 módulo 5, agregamos múltiplos de 5 a 2. Esto da la siguiente lista:

... -13, -8, -3, 2, 7, 12, 17,...

También podemos escribir esto usando notación de conjunto y decir que

{$a \in \mathbb{Z}| a \equiv 2$(mod 5)} = {... -13, -8, -3, 2, 7, 12, 17,...}

Comprobación de Progreso 3.4 (Congruencia Modulo 8)

Determinar al menos ocho enteros diferentes que son congruentes a 5 módulo 8.
Useetbuildernotationandtherostermetodo para especificarlostofallenteros
que son congruentes a 5 módulo 8.
Elija dos enteros que sean congruentes a 5 módulo 8 y agréguelos. Después repita esto para al menos otros cinco pares de enteros que sean congruentes a 5 módulo 8.
Explique por qué todas las sumas que se obtuvieron en la Parte (3) son congruentes con 2 módulo 8.

Contestar: Agrega textos aquí. No elimine primero este texto.

Estudiaremos el concepto de módulo$n$ de congruencia con mucho más detalle más adelante en el texto. Por ahora, trabajaremos con la definición de módulo de congruencia$n$ en el contexto de las pruebas. Por ejemplo, todos los ejemplos utilizados en Progress Check 3.4deberían proporcionar evidencia de que la siguiente proposición es cierta.

Proposición 3.5.

Para todos los enteros$a$ y$b$, si$a \equiv 5$ (mod 8) y$b \equiv 5$ (mod 8), entonces ($a$+$b$)$\equiv$ 2 (mod 8).

Comprobación de Progreso 3.6 (Proposición de Prueba 3.5)

Utilizaremos “preguntas atrasadas” y “preguntas hacia adelante” para ayudar a construir una prueba para la Proposición 3.5. Entonces, podríamos preguntar, “¿Cómo probamos que ($a$+$b$)$\equiv$ 2 (mod 8)” Una forma de responder a esto es usar la definición de congruencia y afirmar que ($a$+$b$)$\equiv$ 2 (mod 8) siempre que 8 divide ($a + b - 2$).

Utilice la definición de divisiones para determinar una manera de probar que 8 divide ($a + b - 2$).

Pasamos ahora a lo que sabemos y preguntamos, “¿Qué podemos concluir a partir de los supuestos que$a \equiv 5$ (mod 8) y$b \equiv 5$ (mod 8).” Podemos utilizar nuevamente la definición de congruencia y concluir que 8 divide ($a$- 5) y 8 divide ($b$- 5).
Utilizar la definición de divisiones para sacar conclusiones con base en los hechos que 8 divide ($a$- 5) y 8 divide ($b$- 5).
Resolver una ecuación de la parte (2) para$a$ y para$b$.
Utilice los resultados de la parte (3) para demostrar que 8 divide ($a + b - 2$).
Escriba un comprobante para la Proposición 3.5.

Contestar: Agrega textos aquí. No elimine primero este texto.

Pautas adicionales de escritura

Ahora estaremos escribiendo muchas pruebas, y es importante asegurarnos de que escribimos de acuerdo con las pautas aceptadas para que nuestras pruebas puedan ser entendidas por otros. En el Capítulo 1 se introdujeron algunas pautas de escritura. Los primeros cuatro lineamientos de escritura que se dan a continuación pueden considerarse lineamientos generales, y los tres últimos pueden considerarse como lineamientos técnicos específicos de la escritura en matemáticas.

Conoce a tu audiencia. Todo escritor debe tener una idea clara de la audiencia prevista para un escrito. De esa manera, el escritor puede dar la cantidad correcta de información al nivel adecuado de sofisticación para comunicarse de manera efectiva. Esto es especialmente cierto para la escritura matemática. Por ejemplo, si un matemático está escribiendo una solución a un problema de libro de texto para un manual de soluciones para instructores, la escritura sería breve con muchos detalles omitidos. Sin embargo, si la escritura fuera para un manual de solución de los estudiantes, se incluirían más detalles.
Use oraciones completas y estructura de párrafos adecuada. La buena gramática es una parte importante de cualquier escritura. Por lo tanto, cumplir con las reglas aceptadas de la gramática. Preste mucha atención a la estructura de las oraciones. Escribe pruebas usando frases completas pero evita las oraciones continuas. Además, no olvides la puntuación, y siempre usa un corrector ortográfico cuando uses un procesador de textos.
Mantenlo simple. A menudo es difícil entender un argumento matemático sin importar lo bien que esté escrito. No dejes que tu escritura ayude a que sea más difícil para el lector. Utilizar oraciones simples, declarativas y párrafos cortos, cada uno con un simple punto.
Escribe un primer borrador de tu comprobante y luego revísalo. Recuerda que se escribe una prueba para que los lectores sean capaces de leer y entender el razonamiento en la prueba. Sea claro y conciso. Incluya detalles pero no divague. No estar satisfecho con el primer borrador de una prueba. Léela y refínala. Al igual que cualquier actividad que valga la pena, aprender a escribir bien las matemáticas requiere práctica y trabajo duro. Esto puede ser frustrante. Todos pueden estar seguros de que habrá algunas pruebas que son difíciles de construir, pero recuerden que las pruebas son una parte muy importante de las matemáticas. Así que trabaja duro y diviértete.
No usar$\ast$ para multiplicación ni para exponentes. Deja este tipo de notación para escribir código de computadora. El uso de esta notación dificulta la lectura de los humanos. Además, evite usar/para división cuando use una fracción compleja.

Por ejemplo, es muy difícil de leer ($x^3 - 3x^2 + 1/2)/(2x/3 - 7$); la fracción

\[\dfrac{x^3 - 3x^2 + \dfrac{1}{2}}{\dfrac{2x}{3} - 7}\]

es mucho más fácil de leer.
No utilice un símbolo matemático al comienzo de una oración. Por ejemplo, no debemos escribir, “Que n sea un entero. n es un entero impar siempre que.” A muchas personas les resulta difícil de leer y muchas veces tienen que volver a leerlo para entenderlo. Sería mejor escribir: “Un entero n es un número entero impar siempre que..”
Usa el inglés y minimiza el uso de la notación engorrosa. No utilice los símbolos especiales para cuantificadores$\forall$ (para todos),$exists$ (existe), (tal que), o$\epsilon$$\therefore$ (por lo tanto) en la escritura matemática formal. A menudo es más fácil escribir, y generalmente más fácil de leer, si se usan las palabras en inglés en lugar de los sym- bols. Por ejemplo, por qué hacer que el lector interprete

\[(\forall x \in \mathbb{R})(\exists y \in \mathbb{R})(x + y = 0)\]

Cuando es posible escribir
Para cada número real$x$, existe un número real$y$ tal que$x + y = 0$, o, más sucintamente (si apropiado),

Cada número real tiene una inversa aditiva.

Ejercicio para la sección 3.1

Demostrar cada una de las siguientes declaraciones:

(a) Para todos los enteros$a$$b$,, y$c$ con$a \ne 0$, si$a | b$ y$a | c$, entonces$a | (b-c)$.
(b) Para cada uno$n \in \mathbb{Z}$, si$n$ es un entero impar, entonces$n^3$ es un entero impar.
(c) Por cada entero$a$, si 4 divide ($a$- 1), entonces 4 divide ($a^2$- 1).
Para cada una de las siguientes, use un contraejemplo para probar que la declaración es falsa.

(a) Por cada número natural impar$n$, si$n > 3$, entonces 3 divide ($n^2$- 1).
(b) Por cada número natural$n$, ($3 \cdot 2^n + 2 \cdot 3^n + 1$) es un número primo.
(c) Para todos los números reales$x$ y$y$,$\sqrt{x^2 + y^2} > 2xy$.
(d) Por cada entero$a$, si 4 divide ($a^2$- 1), entonces 4 divide ($a$- 1).
Determinar si cada una de las siguientes afirmaciones es verdadera o falsa. Si una declaración es verdadera, entonces escriba una prueba formal de esa declaración, y si es falsa, entonces proporcione un contraejemplo que demuestre que es falsa.

(a) Para todos los enteros$a$,$b$, y$c$ con$a \ne 0$, si$a | b$, entonces$a | (bc)$.
(b) Para todos los enteros$a$ y$b$ con$a \ne 0$, si$6 | (ab)$, entonces$6 | a$ o$6 | b$.
(c) Para todos los enteros$a$,$b$ y$c$ con$a \ne 0$, si$a$ divide ($b$- 1) y$a$ divide ($c$-1), entonces$a$ divide ($bc$- 1).
(d) Por cada entero$n$, si 7 divide ($n^2 - 4$), entonces 7 divide ($n - 2$).
(e) Por cada entero$n$,$4n^2 + 7n + 6$ es un entero impar.
(f) Por cada entero impar$n$,$4n^2 + 7n + 6$ es un entero impar
(g) Para todos los enteros$a$$b$,$d \ne 0$, y$d$ con, si$d$ divide ambos$a - b$ y$a + b$, luego$d$ divide$a$.
(h) Para todos los enteros$a$$b$,, y$c$ con$a \ne 0$, si$a | (bc)$, entonces$a | b$ o$a | c$.
(a) Si$x$ y$y$ son enteros y$xy = 1$, explicar por qué$x = 1$ o$x = -1$.
b) ¿Es verdadera o falsa la siguiente proposición?
Para todos los enteros distintos de cero$a$ y$b$, si$a | b$ y$b | a$, entonces$a = \pm b$.
Demostrar la siguiente proposición:

Let$a$ be an integer. Si existe un entero$n$ tal que$a | (4n + 3)$ y$a | (2n + 1)$, entonces$a = 1$ o$a = -1$.

Pista: Usa el hecho de que los únicos divisores de 1 son 1 y -1.
Determinar si cada una de las siguientes afirmaciones es verdadera o falsa. Si una declaración es verdadera, entonces escriba una prueba formal de esa declaración, y si es falsa, entonces proporcione un contraejemplo que demuestre que es falsa. (a) Por cada entero$a$, si existe un entero$n$ tal que$a$ divide ($8n + 7$) y$a$ divide ($4n + 1$), entonces$a$ divide 5.
(a) Por cada entero$a$, si existe un entero$n$ tal que$a$ divide ($9n + 5$) y$a$ divide ($6n + 1$), entonces$a$ divide 7.
(c) Por cada entero$n$, si$n$ es impar, entonces 8 divide ($n^4 + 4n^2 + 11$).
(d) Por cada entero$n$, si$n$ es impar, entonces 8 divide ($n^4 + n^2 + 2n$).
Dejar$a$ ser un entero y dejar$n \in \mathbb{N}$.

(a) Demostrar que si$a \equiv 0$ (mod$n$), entonces$n | a$.
b) Demostrar que si$n | a$, entonces$a \equiv 0$ (mod$n$).
Dejar$a$ y$b$ ser enteros. Demostrar que si$a \equiv 2$ (mod 3) y$b \equiv 2$ (mod 3), entonces

(a)$a + b \equiv 1$ (mod 3).
b)$a \cdot b \equiv 1$ (mod 3).
Dejar$a$ y$b$ ser enteros. Demostrar que si$a \equiv 7$ (mod 8) y$b \equiv 3$ (mod 8), entonces

(a)$a + b \equiv 2$ (mod 8).
b)$a \cdot b \equiv 5$ (mod 8).
Determinar si cada una de las siguientes proposiciones es verdadera o falsa. Justificar cada conclusión.

(a) Para todos los enteros$a$ y$b$, si$ab \equiv 0$ (mod 6), entonces$a \equiv 0$ (mod 6) o$b \equiv$ (mod 6).
(b) Por cada entero$a$, si$a \equiv 2$ (mod 8), entonces$a^2 \equiv 4$ (mod 8).
(c) Por cada entero$a$, si$a^2 \equiv 4$ (mod 8), entonces$a \equiv 2$ (mod 8).
Dejar$n$ ser un número natural. Demostrar cada uno de los siguientes:

(a) Por cada entero$a$,$a \equiv a$ (mod$n$).
A esto se le llama la propiedad reflexiva de módulo de congruencia$n$.
(b) Por cada entero$a$ y$b$, si$a \equiv b$ (mod$n$), entonces$b \equiv a$ (mod$n$).
A esto se le llama la propiedad simétrica de módulo de congruencia$n$.
(c) Por cada entero$a$,$b$ y\ 9c\), si$a \equiv b$ (mod$n$) y$b \equiv c$ (mod$n$), entonces$a \equiv c$ (mod$n$).
A esto se le llama la propiedad transitiva de módulo de congruencia$n$.
Dejar$n$ ser un número natural y dejar$a$$b$,$c$,, y$d$ ser enteros. Demostrar cada uno de los siguientes.

(a) Si$a \equiv b$ (mod$n$) y$c \equiv d$ (mod$n$), entonces$(a + c) \equiv (b + d)$ (mod$n$).
(b) Si$a \equiv b$ (mod$n$) y$c \equiv d$ (mod$n$), entonces$ac \equiv bd$ (mod$n$).
(a) Dejar$a$,$b$, y$c$ ser números reales con$a \ne 0$. Explicar cómo usar una parte de la fórmula cuadrática (llamada discriminante) para determinar si la ecuación cuadrática$ax^2 + bx + c = 0$ tiene dos soluciones de números reales, una solución de número real o ninguna solución de número real. (Véase Ejercicio (11) en la Sección 1.2 para una declaración de la fórmula cuadrática.)
(b) Demostrar que si$a$$b$,, y$c$ son números reales para los cuales$a > 0$ y$c < 0$, entonces una solución de la ecuación cuadrática$ax^2 + bx + c = 0$ es un número real positivo.

(c) Demostrar que si$a$$b$,, y$c$ son números reales, si$a \ne 0$,$b > 0$ y$\dfrac{b}{2} < \sqrt{ac}$, entonces la ecuación cuadrática no$ax^2 + bx + c = 0$ tiene solución numérica real.
Dejar$h$ y$k$ ser números reales y dejar que$r$ sea un número positivo. La ecuación para un círculo cuyo centro está en el punto ($h$,$k$) y cuyo radio es$r$ es

\[(x - h)^2 + (y - k)^2 = r^2\].

También sabemos que si$a$ y$b$ son números reales, entonces

$\bullet$ El punto ($a$,$b$) está dentro del círculo si$(a - h)^2 + (b - k)^2 < r^2$.
$\bullet$El punto ($a$,$b$) está en el círculo si$(a - h)^2 + (b - k)^2 = r^2$.
$\bullet$El punto ($a$,$b$) está fuera del círculo si$(a - h)^2 + (b - k)^2 > r^2$.

Demostrar que todos los puntos sobre o dentro del círculo cuya ecuación es$(x - 1)^2 + (y - 2)^2 = 4$ están dentro del círculo cuya ecuación es$x^2 + y^2 = 26$.
$r$Sea un número real positivo. La ecuación para un círculo de radio$r$ cuyo centro es el origen es$x^2 + y^2 = r^2$.

a) Utilizar diferenciación implícita para determinar$\dfrac{dy}{dx}$.
b) Sea ($a$,$b$) un punto en el círculo con$a \ne 0$ y$b \ne 0$. Determinar la pendiente de la línea tangente al círculo en el punto ($a$,$b$).
(c) Demostrar que el radio del círculo al punto ($a$,$b$) es perpendicular a la línea tangente al círculo en el punto ($a$,$b$). Pista: Dos líneas (ninguna de las cuales es horizontal) son perpendiculares si y solo si los productos de sus pendientes son iguales a -1.
Determinar si cada una de las siguientes afirmaciones es verdadera o falsa. Proporcionar un contraejemplo para las declaraciones que son falsas y proporcionar una prueba completa de las que son verdaderas.

(a) Para todos los números reales$x$ y$y$,$\sqrt{xy} \le \dfrac{x + y}{2}$.
b) Para todos los números reales$x$ y$y$,$xy \le (\dfrac{x + y}{2})^2$.
(c) Para todos los números reales no negativos$x$ y$y$,$\sqrt{xy} \le \dfrac{x + y}{2}$.
Utilizar uno de los verdaderos en igualdades en el Ejercicio (16) para acreditar la siguiente proposición.

Por cada número real$a$, el valor de$x$ que da el valor máximo de$y = x (a - x)$ es$x = \dfrac{a}{2}$.
a) Exponer el Teorema de Pitágoras para los triángulos rectos.
Los diagramas de la Figura 3.1 serán utilizados para los problemas en este ejercicio.
(b) En el diagrama de la izquierda,$x$ se encuentra la longitud de un lado del triángulo equilátero y$h$ es la longitud de una altitud del triángulo equilátero. El etiquetado en el diagrama muestra el hecho de que la altitud cruza la base del triángulo equilátero en el punto medio de la base. Utilice la
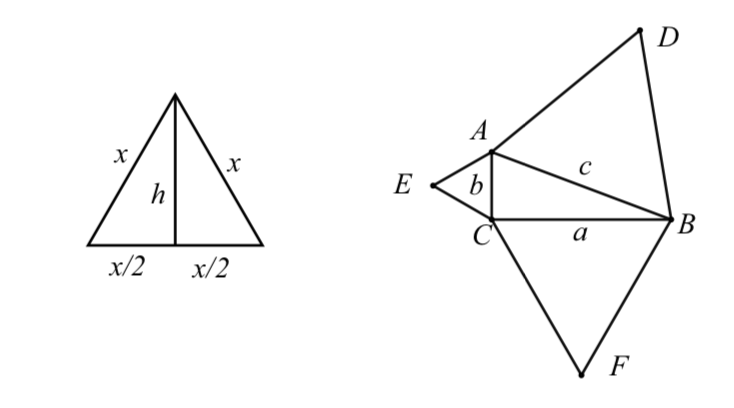
$2019-02-11 4.04.29.png$
Figura 3.1: Diagramas para el Ejercicio (18) Teorema de
Pitágoras para demostrar que el área de este triángulo equilátero es$\dfrac{\sqrt3}{4} x^2$.
(c) En el diagrama de la derecha,$\bigtriangleup ABC$ se encuentra un triángulo rectángulo. Además, ha habido un triángulo equilátero construido a cada lado de este triángulo rectángulo. Demostrar que el área del triángulo equilátero sobre la hipotenusa es igual a la suma de las áreas de los triángulos equiláteros construidos en los otros dos lados del triángulo rectángulo.
Evaluación de pruebas
Este tipo de ejercicio aparecerá frecuentemente en el libro. En cada caso, hay una prueba propuesta de una proposición. Sin embargo, la proposición puede ser verdadera o puede ser falsa.

$\bullet$Si una proposición es falsa, la prueba propuesta es, por supuesto, incorrecta. En esta situación, hay que encontrar el error en la prueba y luego proporcionar un contraejemplo que demuestre que la proposición es falsa.
$\bullet$Si una proposición es cierta, la prueba propuesta aún puede ser incorrecta. En este caso, debe determinar por qué la prueba es incorrecta y luego escribir una prueba correcta utilizando las pautas de escritura que se han presentado en este libro.
$\bullet$Si una proposición es verdadera y la prueba es correcta, debe decidir si la prueba está bien escrita o no. Si está bien escrito, entonces simplemente debe indicar que esta es una excelente prueba y no necesita revisión. Por otra parte, si la prueba no está bien escrita, entonces deberá revisar la prueba así escribiéndola de acuerdo a los lineamientos que se presentan en este texto.

a) Proposición. Si m es un entero par, entonces$5m + 4$ es un entero par.

Prueba. Eso lo vemos$5m + 4 = 10n + 4 = 2(5n + 2)$. Por lo tanto,$5m + 4$ es un entero par.

b) Proposición. Para todos los números reales$x$ y$y$, si$x \ne y$,$x > 0$, y$y > 0$, entonces$\dfrac{x}{y} + \dfrac{y}{x} > 2$.

Prueba. Ya que$x$ y$y$ son números reales positivos,$xy$ es positivo y podemos multiplicar ambos lados de la desigualdad por$xy$ obtener

\[(\dfrac{x}{y} + \dfrac{y}{x}) \cdot xy > 2 \cdot xy\]
\[x^2 + y^2 > 2xy\].

Al combinar todos los términos en el lado izquierdo de la desigualdad, vemos eso$x^2 - 2xy + y^2 > 0$ y luego al factorizar el lado izquierdo, obtenemos$(x - y)^2 > 0$. Desde$x \ne y$,$(x - y) \ne 0$ y así$(x - y)^2 > 0$. Esto prueba que si$x \ne y$,$x > 0$, y$y > 0$, cualquiera$y > 0$, entonces$\dfrac{x}{y} + \dfrac{y}{x} > 2$.

c) Proposición. Para todos los enteros$a$,$b$, y$c$, si$a | (bc)$, entonces$a | b$ o$a | c$.

Comprobante. Suponemos que$a$$b$,, y$c$ son enteros y eso$a$ divide$bc$. Entonces, existe un entero$k$ tal que$bc = ka$. Ahora factorizamos$k$ como$k = mn$, dónde$m$ y$n$ son enteros. Entonces vemos eso

\[bc = mna\].

Esto significa que$b = ma$ o$c = na$ y por lo tanto,$a | b$ o$a | c$.

d) Proposición. Para todos los enteros positivos$a$,$b$, y$c$,$(a^b)^c = a ^(b^c)$.
Esta proposición es falsa como lo muestra el siguiente contraejemplo: Si dejamos$a = 2$,$b = 3$, y$c = 2$, entonces

\[(a^b)^c = a ^{b^c}\]
\[(2^3)^2 = 2 ^{3^2}\]
\[8^2 = 2^9\]
\[64 \ne 512\]

Exploraciones y actividades
Congruencia Modulo 6

(a) Encuentra varios enteros que son congruentes a 5 módulo 6 y luego cuadrar cada uno de estos enteros.
(b) Por cada entero$m$ de la Parte (20a), determinar un entero$k$ para que$0 \le k <6$ y$m^2 \equiv k$ (mod 6), luego...
(c) Con base en el trabajo de la Parte (20b), complete la siguiente conjetura:

Para cada entero$m$, si$m \equiv 5$ (mod 6), entonces...
d) Completar una tabla de know show para la conjetura de la Parte (20c) o escribir una prueba de la conjetura.
Triples pitagóricos. Tres números naturales$a$,$b$, y$c$ con$a < b < c$ se llaman triples pitagóricos siempre que$a^2 + b^2 = c^2$. Ver Ejercicio (13) en la página 29 en la Sección 1.2. Tres números naturales se denominan números naturales consecutivos si se pueden escribir en la forma$m$,$m$ + 1, y$m$ + 2, donde$m$ es un número natural.

a) Determinar todas las triples pitagóricas consistentes en tres números naturales consecutivos. (Exponer un teorema y probarlo.)
(b) Determinar todas las triples pitagóricas que puedan escribirse en la forma$m$$m + 7$, y$m + 8$, dónde$m$ es un número natural. Exponer un teorema y probarlo.

Contestar: Agrega textos aquí. No elimine primero este texto.

Paso	Conoce	Razón
\(P\)	\(a\),\(b\),\(c \in \mathbb{Z}\),\(a \ne 0\),\(b \ne 0\),\(a \| b\) y\(b \| c\)	Hipótesis
\(P\)1	\((\exists s \in \mathbb{Z})(b = a \cdot s)\) \((\exists t \in \mathbb{Z})(c = b \cdot t)\)	Definición de “Divide”
\(P\)2	\(c = (a \cdot s) \cdot t\)	Sustitución por\(b\)
\(P\)3	\(c = a \cdot (s \cdot t\))	Propiedad asociativa de la multiplicación
\(Q\)1	\((\exists q \in \mathbb{Z})(c = a \cdot q)\)	Paso\(P\) 3 y las propiedades de cierre de los enteros
\(Q\)	\(a \| c\)	Definición de “divide”