4.1: El principio de inducción matemática
- Page ID
- 116136
Uno de los conjuntos más fundamentales en matemáticas es el conjunto de números naturales\(\mathbb{N}\). En esta sección, aprenderemos una nueva técnica de prueba, llamada inducción matemática, que a menudo se utiliza para probar declaraciones de la forma\((\forall n \in \mathbb{N})(P(n))\). En la Sección 4.2, aprenderemos a extender este método a declaraciones de la forma\((\forall n \in T) (P(n))\), donde\(T\) se encuentra un cierto tipo de subconjunto de los enteros\(\mathbb{Z}\).
Para cada número natural\(n\), deje\(P(n)\) ser la siguiente frase abierta:
4 divide\((5^n - 1)\).
- ¿Esta frase abierta se convierte en una verdadera declaración cuando\(n = 1\)? Es decir, es 1 en el conjunto de verdad de\(P(n)\)?
- ¿Esta frase abierta se convierte en una verdadera declaración cuando\(n = 2\)? Es decir, es 2 en el conjunto de verdad de\(P(n)\)?
- Elija al menos cuatro números naturales más y determine si la oración abierta es verdadera o falsa para cada una de sus elecciones.
Todos los ejemplos que se utilizaron deben aportar evidencia de que la siguiente proposición es cierta:
Por cada número natural\(n\), se divide 4\((5^n - 1)\).
Debemos tener en cuenta que no importa cuántos ejemplos probemos, no podemos probar esta proposición con una lista de ejemplos porque nunca podremos verificar si 4 divisiones\((5^n - 1)\) por cada número natural\(n\). La inducción matemática proporcionará un método para probar esta proposición.
Por otro ejemplo, para cada número natural\(n\), ahora dejamos\(Q(n)\) ser la siguiente frase abierta:
\[1^2 + 2^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}.\]
La expresión en el lado izquierdo de la ecuación anterior es la suma de los cuadrados de los primeros números\(n\) naturales. Entonces cuando\(n = 1\), el lado izquierdo de la ecuación (4.1.1) es\(1^2\). Cuando\(n = 2\), el lado izquierdo de la ecuación (4.1.1) es\(1^2 + 2^2\).
- ¿Se\(Q(n)\) convierte en una verdadera declaración cuando
\(\bullet\ n = 1\)? (¿Es 1 en la verdad conjunto de\(Q(n)\)?
\(\bullet\ n = 2\)? (¿Es 1 en la verdad conjunto de\(Q(n)\)?
\(\bullet\ n = 3\)? (¿Es 1 en la verdad conjunto de\(Q(n)\)? - Elija al menos cuatro números naturales más y determine si la oración abierta es verdadera o falsa para cada una de sus elecciones. Una mesa con las columnas\(n\),\(1^2 + 2^2 + ... + n^2\), y\(\dfrac{n(n + 1)(2n + 1)}{6}\) puede ayudarte a organizar tu trabajo.
Todos los ejemplos que hemos explorado, deberían indicar que la siguiente proposición es cierta:
Por cada número natural\(n\),\ (1^2 + 2^2 +... + n^2 =\ dfrac {n (n + 1) (2n + 1)} {6}.\]
En esta sección, aprenderemos a utilizar la inducción matemática para probar esta afirmación.
Intuitivamente, los números naturales comienzan con el número 1, y luego hay 2, luego 3, luego 4, y así sucesivamente. ¿Este proceso de “comenzar con 1” y “agregar 1 repetidamente” da como resultado todos los números naturales? Utilizaremos el concepto de conjunto inductivo para explorar esta idea en esta actividad.
Un conjunto\(T\) que es un subconjunto de\(\mathbb{Z}\) es un conjunto inductivo siempre que para cada entero\(k\), si\(k \in T\), entonces\(k + 1 \in T\).
- Explique cuidadosamente lo que significa decir que un subconjunto\(T\) de los enteros no\(\mathbb{Z}\) es un conjunto inductivo. Esta descripción debe utilizar un cuantificador existencial.
- Utilice la definición de un conjunto inductivo para determinar cuáles de los siguientes conjuntos son conjuntos inductivos y cuáles no. No se preocupe por las pruebas formales, pero si un conjunto no es inductivo, asegúrese de proporcionar un contraejemplo específico que demuestre que no es inductivo.
(a)\(A = \{1, 2, 3, ..., 20\}\)
(b) El conjunto de números naturales,\(\mathbb{N}\)
(c)\(B = \{n \in \mathbb{N} | n \ge 5\}\)
(d)\(S = \{n \in \mathbb{Z} | n \ge -3\}\)
(e)\(R = \{n \in \mathbb{Z} | n \le 100\}\)
(f) El conjunto de números enteros,\(\mathbb{Z}\)
(g) El conjunto de números naturales impares. - Esta parte explorará una de las ideas matemáticas subyacentes para una prueba por inducción. Asumir eso\(T \subseteq \mathbb{N}\) y asumir que\(1 \in T\) y que\(T\) es un conjunto inductivo. Usa la definición de un conjunto inductivo para responder a cada uno de los siguientes: a
)\(2 \in T\) ¿Es? Explique.
b) ¿Es\(3 \in T\)? Explique.
(c) ¿Es\(4 \in T\)? Explique.
d) ¿Es\(100 \in T\)? Explique.
e) ¿Crees eso\(T = \mathbb{N}\)? Explique.
Conjuntos Inductivos
Las dos oraciones abiertas en Preview Activity\(\PageIndex{1}\) parecían ser ciertas para todos los valores de\(n\) en el conjunto de números naturales,\(\mathbb{N}\). Es decir, los ejemplos en esta actividad de previsualización aportaron evidencia de que las dos afirmaciones siguientes son ciertas.
- Por cada número natural\(n\), se divide 4\((5^n - 1)\).
- Por cada número natural\(n\),\(1^2 + 2^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}.\)
Una forma de probar declaraciones de esta forma utiliza el concepto de un conjunto inductivo introducido en Actividad previa\(\PageIndex{2}\). La idea es probar que si un número natural hace que la oración abierta sea verdadera, entonces la siguiente también hace verdadera la oración abierta. Es así como manejamos la frase “y así sucesivamente” al tratar con los números naturales. En Preview Activity\(\PageIndex{2}\), vimos que los sistemas\(\mathbb{N}\) numéricos\(\mathbb{Z}\) y y otros conjuntos son inductivos. Lo que estamos tratando de hacer es de alguna manera distinguir\(\mathbb{N}\) de los otros conjuntos inductivos. La forma de hacerlo fue sugerida en la Parte (3) de Vista previa de Actividad\(\PageIndex{2}\). A pesar de que no lo vamos a probar, la siguiente afirmación debería parecer cierta.
Declaración 1: Para cada subconjunto\(T\) de\(\mathbb{N}\), si\(1 \in T\) y\(T\) es inductivo, entonces\(T = \mathbb{N}\).
Observe que los enteros,\(\mathbb{Z}\), y el conjunto\(S = \{n \in \mathbb{Z} | n \ge - 3\}\) ambos contienen 1 y ambos son inductivos, pero ambos contienen números distintos de los números naturales. Por ejemplo, la siguiente declaración es falsa:
Declaración 2: Para cada subconjunto\(T\) de\(\mathbb{Z}\), si\(1 \in T\) y\(T\) es inductivo, entonces\(T = \mathbb{Z}\).
El conjunto\(S = \{n \in \mathbb{Z} | n \ge - 3\} = \{-3, -2, -1, 0, 1, 2, 3, ...\}\) es un contraejemplo que demuestra que esta afirmación es falsa.
Supongamos que T es un subconjunto inductivo de los números enteros. ¿Cuáles de las siguientes afirmaciones son verdaderas, cuáles son falsas y para cuáles no es posible decir?
- \(1 \in T\)y\(5 \in T\).
- Si\(1 \in T\), entonces\(5 \in T\).
- Si\(5 \notin T\), entonces\(2 \notin T\).
- Para cada entero\(k\), si\(k \in T\), entonces\(k + 7 \in T\).
- Para cada entero\(k\),\(k \notin T\) o\(k + 1 \in T\).
- Existe un entero\(k\) tal que\(k \in T\) y\(k + 1 \notin T\).
- Para cada entero\(k\), si\(k + 1 \in T\), entonces\(k \in T\).
- Para cada entero\(k\), si\(k + 1 \notin T\), entonces\(k \notin T\).
- Contestar
-
Agrega textos aquí. No borre primero este texto.
El principio de la inducción matemática
Si bien probamos que la Declaración (2) es falsa, en este texto, no vamos a probar que la Declaración (1) es cierta. Una razón para ello es que realmente no tenemos una definición formal de los números naturales. No obstante, debemos estar convencidos de que la Declaración (1) es cierta. Esto lo resolvemos haciendo de la Declaración (1) un axioma para los números naturales para que éste se convierta en una de las características definitorias de los números naturales.
Si\(T\) es un subconjunto de\(\mathbb{N}\) tal que
- \(1 \in T\), y
- Por cada\(k \in \mathbb{N}\), si\(k \in T\), entonces\((k + 1) \in T\).
Entonces\(T = \mathbb{N}\).
Uso del principio de inducción matemática
El uso principal del Principio de Inducción Matemática es acreditar declaraciones de la forma
\((\forall n \in \mathbb{N}) (P(n))\).
donde\(P(n)\) hay alguna frase abierta. Recordemos que una afirmación universalmente cuantificada como la anterior es verdadera si y sólo si el conjunto de verdad T de la oración abierta\(P(n)\) es el conjunto\(\mathbb{N}\). Por lo que nuestro objetivo es probarlo\(T = \mathbb{N}\), que es la conclusión del Principio de Inducción Matemática. Para verificar la hipótesis del Principio de Inducción Matemática, debemos
- \(1 \in T\)Demuéstralo. Es decir, demostrar que\(P(1)\) es verdad.
- Demostrar que si\(k \in T\), entonces\((k + 1) \in T\). Es decir, probar que si\(P(k)\) es verdad, entonces\(P(k + 1)\) es verdad.
El primer paso se llama el paso base o el paso inicial, y el segundo paso se llama el paso inductivo. Esto significa que una prueba por inducción matemática tendrá la siguiente forma:
Para probar:\((\forall n \in \mathbb{N}) (P(n))\)
Paso de base: Demostrar\(P(1)\). \
Paso inductivo: Demostrar que para cada uno\(k \in \mathbb{N}\), si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto.
Entonces podemos concluir que\(P(n)\) es cierto para todos\(n \in \mathbb{N}\)
Obsérvese que en el paso inductivo, queremos probar que la declaración condicional “para cada uno\(k \in \mathbb{N}\), si\(P(k)\) entonces\(P(k + 1)\)” es verdadera. Entonces iniciaremos el paso inductivo asumiendo que eso\(P(k)\) es cierto. Esta suposición se denomina hipótesis inductiva o hipótesis inductiva.
La clave para construir una prueba por inducción es descubrir cómo\(P(k + 1)\) se relaciona con\(P(k)\) para un número natural arbitrario\(k\). Por ejemplo, en Preview Activity\(\PageIndex{1}\), una de las frases abiertas\(P(n)\) fue
\(1^2 + 2^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}.\)
A veces ayuda mirar algunos ejemplos específicos como\(P(2)\) y\(P(3)\). La idea no es sólo hacer los cómputos, sino ver cómo se relacionan los enunciados. Esto a veces se puede hacer escribiendo los detalles en lugar de hacer cálculos de inmediato.
\ begin {eqnarray}
\\\\\\ &P (2) &\\\\\\\\\ &is&\\\\\\\\\\\\\\\\\\\\\ 1^2 + 2^2 &=&\ dfrac {2\ cdot 3\ cdot 5} {6}\
\\\\\\\ &P (3) &\\\\\\\\ &is&\\\\\\\\\\\\\ 1^2 + 2^2 + 3^2 &=&\ dfrac {3\ cdot 4\ cdot 7} {6}
\ end {eqnarray}
En este caso, la clave es el lado izquierdo de cada ecuación. El lado izquierdo de\(P(3)\) se obtiene del lado izquierdo de\(P(2)\) agregando un término, que es\(3^2\). Esto sugiere que podríamos ser capaces de obtener la ecuación para\(P(3)\) sumando\(3^2\) a ambos lados de la ecuación\(P(2)\). Ahora para el caso general, si\(k \in \mathbb{N}\), lo miramos\(P(k + 1)\) y comparamos con\(P(k)\).
\ begin {eqnarray}
\\\\ P (k)\\\\ &is&\\\\\\\\\ 1^2 + 2^2 +... + k^2 =\ dfrac {k (k + 1) (2k + 1)} {6}\\\
\ P (k + 1)\\ &is&\\ 1^2 + 2^2 +... + (k + 1) ^2 =\ dfrac {(k + 1) [(k + 1) + 1] [2 (k + 1) + 1]} {6}
\ end {eqnarray}
La clave es mirar el lado izquierdo de la ecuación\(P(k + 1)\) y darse cuenta de lo que significa esta notación. Significa que estamos sumando los cuadrados de los primeros números\(k + 1\) naturales. Esto significa que podemos escribir
\(1^2 + 2^2 + ... + (k + 1)^2 = 1^2 + 2^2 + ... + k^2 + (k + 1)^2.\)
Esto nos muestra que el lado izquierdo de la ecuación para se\(P(k + 1)\) puede obtener del lado izquierdo de la ecuación para\(P(k)\) sumando\((k + 1)^2\). Esta es la motivación para probar el paso inductivo en la siguiente prueba.
Por cada número natural\(n\),
\(1^2 + 2^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}.\)
- Prueba
-
Utilizaremos una prueba por inducción matemática. Por cada número natural\(n\), dejamos\(P(n)\) ser
\(1^2 + 2^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}.\)
Primero probamos que eso\(P(1)\) es cierto. Observe eso\(\dfrac{1(1 + 1)(2 \cdot 1 + 1)}{6} = 1\). Esto demuestra que
\ (1^2 =\ dfrac {1 (1 + 1) (2\ cdot 1 + 1} {6},
lo que demuestra que eso\(P(1)\) es cierto.
Para el paso inductivo, demostramos que para cada uno\(k \in \mathbb{N}\), si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto. Así que\(k\) seamos un número natural y supongamos que eso\(P(k)\) es cierto. Es decir, supongamos que
\[1^2 + 2^2 + ... + k^2 = \dfrac{k(k + 1)(2k + 1)}{6}.\]
El objetivo ahora es demostrar que eso\(P(k + 1)\) es cierto. Es decir, hay que probar que
\ begin {eqnarray}
1^2 + 2^2 +... + k^2 + (k + 1) ^2 &=&\ dfrac {(k + 1) [(k + 1) + 1] [2 (k + 1) + 1]} {6} {6}.
\ end {eqnarray}Para ello, sumamos\((k + 1)^2\) a ambos lados de la ecuación (1) y reescribimos algebraicamente el lado derecho de la ecuación resultante. Esto da
\ begin {eqnarray}
1^2 + 2^2 +... + k^2 + (k + 1) ^2 &=&\ dfrac {k (k + 1) (2k + 1)} {6} + (k + 1) ^2\
&=&\ dfrac {k (k + 1) (2k + 1) + 6 (k + 1) ^2} {6}\\
&=&\ dfrac {(k + 1) [k (2k + 1) + 6 (k + 1)]} {6}\\
&=&\ dfrac {(k + 1) (2k^2 + 7k + 6)} {6}\\
&=&\ dfrac {(k + 1) (k + 2) (2k + 3) + 6 (k + 1) ^2} {6}
\ end {eqnarray}Comparando este resultado con la ecuación (2), vemos que si\(P(k)\) es verdadero, entonces\(P(k + 1)\) es cierto. De ahí que se haya establecido el paso inductivo, y por el Principio de Inducción Matemática, hemos demostrado que para cada número natural\(n\),\(1^2 + 2^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}.\)
Guideario de escritura
La prueba de la Proposición 4.2 muestra una forma estándar de escribir una prueba de inducción. Al escribir una prueba por inducción matemática, debemos seguir la pauta de que siempre mantenemos informado al lector. Esto quiere decir que al inicio de la prueba, debemos exponer que se utilizará una prueba por inducción. Deberíamos entonces definir claramente la frase abierta (P (n)\) que se utilizará en la prueba.
Notación de suma
El resultado en la Proposición 4.2 podría escribirse usando la notación de suma de la siguiente manera:
\ begin {ecuación*}
\ text {Por cada número natural\(n\)},\ sum_ {j=1} ^n j^2 =\ dfrac {n (n + 1) (2n + 1)} {6}.
\ end {ecuación*}
En este caso, usamos\(j\) para el índice para la suma, y la notación nos\(\sum_{j=1}^n j^2\) dice que sumemos todos los valores de\(j^2\) para\(j\) de 1 a\(n\), inclusive. Es decir,
\ begin {ecuación*}
\ suma_ {j=1} ^n j^2 = 1^2 + 2^2 +... + n^2.
\ end {ecuación*}
Entonces, en la prueba de la Proposición 4.2, dejaríamos\(P(n)\) ser\(\sum_{j=1}^n j^2 = \dfrac{n(n + 1)(2n + 1)}{6}\), y usaríamos el hecho de que para cada número natural\(k\),
\ begin {ecuación*}
\ suma_ {j=1} ^ {k+1} j^2 = (\ sum_ {j=1} ^ {k} j^2) + (k + 1) ^2.
\ end {ecuación*}
- Calcular\(1 + 2 + 3 + ... + n\) y\(\dfrac{n(n+1)}{2}\) para varios números naturales\(n\). ¿Qué observas?
- Usa la inducción matemática para demostrarlo\(1 + 2 + 3 + ... + n = \dfrac{n(n+1)}{2}\). Para ello, que\(P(n)\) sea la oración abierta, "\(1 + 2 + 3 + ... + n = \dfrac{n(n+1)}{2}\).” Para el paso base, observe que la ecuación\(1 = \dfrac{1(1 + 1)}{2}\) muestra que eso\(P(1)\) es cierto. Ahora vamos a\(k\) ser un número natural y supongamos que eso\(P(k)\) es cierto. Es decir, asuma eso
\[1 + 2 + 3 + ... + k = \dfrac{k(k+1)}{2},\]
y complete la prueba.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Algunos comentarios sobre la inducción matemática
- El paso base es una parte esencial de una prueba por inducción. Ver Ejercicio (19) para ver un ejemplo que demuestre que el paso base es necesario en una prueba por inducción.
- El ejercicio (20) proporciona un ejemplo que muestra que el paso inductivo es también una parte esencial de una prueba por inducción matemática.
- Es importante recordar que el paso inductivo en una prueba de inducción es una prueba de una declaración condicional. Aunque no se utilizó explícitamente el proceso adelante-atrás en el paso inductivo para la Proposición 4.2, se utilizó implícitamente en la discusión previa a la Proposición 4.2. La pregunta clave fue: “¿Cómo nos ayuda conocer la suma de los primeros\(k\) cuadrados a encontrar la suma de los primeros\((k + 1)\) cuadrados?”
- Al probar el paso inductivo en una prueba por inducción, la pregunta clave es,
¿Cómo nos\(P(k)\) ayuda saber a probar\(P(k + 1)\)?
En la Proposición 4.2, pudimos ver que la manera de responder a esta pregunta era agregar una cierta expresión a ambos lados de la ecuación dada en\(P(k)\). A veces la relación entre\(P(k)\) y no\(P(k + 1)\) es tan fácil de ver. Por ejemplo, en Preview Activity\(\PageIndex{1}\), exploramos la siguiente proposición:
Por cada número natural\(n\), 4 divisiones\((5^n - 1)\).
Esto quiere decir que la oración abierta\(P(n)\),, es “4 divide”\((5^n - 1)\). Entonces en el paso inductivo, asumimos\(k \in \mathbb{N}\) y que 4 divide\((5^k - 1)\). Esto quiere decir que existe un entero\(m\) tal que
\[5^k - 1 = 4m.\]
en el proceso hacia atrás, el objetivo es demostrar que 4 divide\((5^{k+1} - 1)\). Esto se puede lograr si podemos probar que existe un entero\(s\) tal que ahora
\[5^{k+1} - 1 = 4s.\]
necesitamos ver si hay algo en la ecuación (4.1.15) que pueda usarse en la ecuación (4.1.16). La clave es encontrar algo en la ecuación\(5^k - 1 = 4m\) que esté relacionado con algo similar en la ecuación\(5^{k+1} - 1 = 4s\) En este caso, notamos que
\[5^{k+1} = 5 \cdot 5^k.\]
Entonces si podemos resolver\(5^k - 1 = 4m\) por\(5^k\), podríamos hacer una sustitución por\(5^k\). Esto se hace en la prueba de la siguiente proposición.
Por cada número natural\(n\), 4 divide\((5^n - 1)\).
- Prueba
-
(Prueba por inducción matemática) Por cada número natural\(n\), let\(P(n)\) be “4 divides\((5^n - 1)\)” Primero probamos que\(P(1)\) es cierto. Observe que cuando\(n = 1\),\(5^n - 1 = 4\). Ya que 4 divide 4,\(P(1)\) es cierto.
Para el paso inductivo, demostramos que para todos\(k \in \mathbb{N}\), si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto. Así que\(k\) seamos un número natural y supongamos que eso\(P(k)\) es cierto. Es decir, supongamos que
4 divide\((5^k - 1)\).
Esto significa que existe un entero\(m\) tal que
\(5^k - 1 = 4m.\)
Por lo tanto,
\[5^k = 4m + 1.\]
Para demostrar que eso\(P(k + 1)\) es cierto, debemos demostrar que 4 divide\((5^{k+1} - 1)\). Ya que\(5^{k+1} = 5 \cdot 5^k\), podemos escribir
\[5^{k+1} - 1 = 5 \cdot 5^k - 1.\]
Ahora sustituimos la expresión por 5k de la ecuación (4.1.18) en la ecuación (4.1.19). Esto da
\[\begin{array} {lll} {5^{k + 1} - 1} &{=} &{5\cdot 5^{k} - 1} \\ {} &{=} &{5(4m + 1) - 1} \\ {} &{=} &(20m + 5) - 1\\ {} &{=} & 20m + 4\\ {} &{=} & 4(5m + 1) \end{array}\]
Dado que\((5m + 1)\) es un entero, la ecuación (4.1.20) muestra que 4 divide\((5^{k+1} - 1)\). Por lo tanto, si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto y se ha establecido el paso inductivo. Así, por el principio de Inducción Matemática, por cada número natural\(n\), se divide 4\((5^{n} - 1)\).
La Proposición 4.4 se planteó en términos de “divide”. Podemos usar la congruencia para afirmar una proposición que es equivalente a la Proposición 4.4. La idea es que la oración, 4 divide\((5^{n} - 1)\) significa que\(5^n \equiv 1\) (mod 4). Por lo que la siguiente proposición equivale a la Proposición 4.4.
Por cada número natural\(n\),\(5^n \equiv 1\) (mod 4).
Desde que hemos probado la Proposición 4.4, hemos probado en efecto la Proposición 4.5. Sin embargo, podríamos haber probado primero la Proposición 4.5 utilizando los resultados del Teorema 3.28 de la página 147. Esto se hará en la próxima comprobación de avance.
Para probar la Proposición 4.5, dejamos\(P(n)\) ser\(5^n \equiv 1\) (mod 4) y notamos que\(P(1)\) es cierto desde\(5 \equiv 1\) (mod 4). Para el paso inductivo, dejemos\(k\) ser un número natural y supongamos que eso\(P(k)\) es cierto. Es decir, supongamos que\(5^n \equiv 1\) (mod 4).
- ¿Qué hay que probar para demostrar que\(P(k + 1)\) es verdad?
- Ya que\(5^{k+1} = 5 \cdot 5^k\), multiplique ambos lados de la congruencia\(5^k \equiv 1\) (mod 4) por 5. Los resultados en el Teorema 3.28 de la página 147 justifican este paso.
- Ahora completa la prueba de que para cada uno\(k \in \mathbb{N}\), si\(P(k)\) es verdad, entonces\(P(k + 1)\) es verdadera y completa la prueba de inducción de la Proposición 4.5.
Podría ser agradable comparar las pruebas de las Proposiciones 4.4 y 4.5 y decidir cuál es más fácil de entender.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
- ¿Cuáles de los siguientes conjuntos son conjuntos inductivos? Explique.
a)\(\mathbb{Z}\)
b) c\(\{x \in \mathbb{N} | x \ge 4\}\)
) d\(\{x \in \mathbb{Z} | x \le 10\}\)
) {1, 2, 3,..., 500} - (a) ¿Un conjunto finito y no vacío puede ser inductivo? Explique.
(b) ¿El conjunto vacío es inductivo? Explique. - Utilizar la inducción matemática para probar cada uno de los siguientes:
(a) Por cada número natural\(n\),\(2 + 5 + 8 + \cdot\cdot\cdot + (3n - 1) = \dfrac{n(3n+1)}{2}\).
b) Por cada número natural\(n\),\(1 + 5 + 9 + \cdot\cdot\cdot + (4n - 3) = n(2n - 1)\).
c) Por cada número natural\(n\),\(1^3 + 2^3 + 3^3 + \cdot\cdot\cdot + n^3 = [\dfrac{n(n+1)}{2}]^2\). - Con base en los resultados de la Comprobación de Progreso 4.3 y Ejercicio (3c)\(n \in \mathbb{N}\), si, ¿hay alguna conclusión que pueda hacerse sobre la relación entre la suma\((1^3 + 2^3 + 3^3 + ... + n^3)\) y la suma\((1 + 2 + 3 + \cdot\cdot\cdot + n)\)?
- En lugar de usar la inducción, a veces podemos usar resultados previamente probados sobre una suma para obtener resultados sobre una suma diferente.
(a) Utilizar el resultado de la Comprobación de Progreso4.3 para probar la siguiente proposición:
\[\text{For each natural number \(n\)}, 3 + 6 + 9 + ... + 3n = \dfrac{3n(n + 1)}{2}.\]
(b) Restar\(n\) de cada lado de la ecuación en la Parte (a). En el lado izquierdo de esta ecuación, explique por qué esto se puede hacer restando 1 de cada término en la suma.
(c) Simplificar algebraicamente el lado derecho de la ecuación en la Parte (b) para obtener una fórmula para la suma\(2 + 5 + 8 + ... (3n - 1).\) Compárelo con el Ejercicio (3a). - a) Calcular\(1 + 3 + 5 + \cdot\cdot\cdot + (2n - 1)\) para varios números nuaturales\(n\).
(b) Con base en tu trabajo en ejercicio (6a), si\(n \in \mathbb{N}\), haz una conjetura sobre el valor de la suma\(1 + 3 + 5 + \cdot\cdot\cdot + (2n - 1) = \sum_{j = 1}^n (2j - 1).\)
(c) Usa la inducción matemática para probar tu conjetura en el Ejercicio (6b). - En la Sección 3.1, definimos módulo de congruencia\(n\) para un número natural\(n\), y en la Sección 3.5, usamos el Algoritmo de División para probar que cada entero es congruente\(n\), módulo, con precisamente uno de los enteros 0, 1, 2,\ cdot\ cdot\ cdot,\(n - 1\) (Corolario 3.32).
(a) Encontrar el valor de\(r\) para que\(4 \equiv r\) (mod 3) y\(r \in \{0, 1, 2\}\).
(b) Encontrar el valor de\(r\) para que\(4^2 \equiv r\) (mod 3) y\(r \in \{0, 1, 2\}\).
(c) Encontrar el valor de\(r\) para que\(4^3 \equiv r\) (mod 3) y\(r \in \{0, 1, 2\}\).
(d) Para otros dos valores de\(n\), encontrar el valor de\(r\) para que\(4^n \equiv r\) (mod 3) y\(r \in \{0, 1, 2\}\).
(e) Si\(n \in \mathbb{N}\) hacer una conjetura sobre el valor de\(r\) where\(4^n \equiv r\) (mod 3) y\(r \in \{0, 1, 2\}\). Esta conjetura debe escribirse como una proposición autónoma que incluya un cuantificador apropiado.
(f) Usa la inducción matemática para probar tu conjetura. - Utilizar la inducción matemática para probar cada uno de los siguientes:
(a) Por cada número natural\(n\), 3 divide\((4^n - 1)\).
b) Por cada número natural\(n\), se divide 6\((n^3 - n)\). - En el Ejercicio (7), probamos que para cada número natural\(n\),\(4^n \equiv 1\) (mod 3). Explique cómo se relaciona este resultado con la proposición en el Ejercicio (8a).
- Utilice la inducción matemática para demostrar que para cada número natural\(n\), 3 divisiones\(n^3 + 23n\). Compare esta prueba con la prueba del Ejercicio (18) en la Sección 3.5.
- a) Calcular el valor de\(5^n - 2^n\) para\(n = 1, n = 2, n = 3, n = 4, n = 5\) y\(n = 6\).
(b) Con base en su trabajo en la Parte (a), haga una conjetura sobre los valores de\(5^n - 2^n\) para cada número natural\(n\).
(c) Utilice la inducción matemática para probar su conjetura en la Parte (b). - Dejar\(x\) y\(y\) ser enteros. Demostrar que para cada número natural\(n\),\((x - y)\) divide\((x^n - y^n)\). Explica por qué tu conjetura en el Ejercicio (11) es un caso especial de este resultado.
- Demostrar la Parte (3) del Teorema 3.28 de la Sección 3.4. Dejar\(n \in \mathbb{N}\) y dejar\(a\) y\(b\) ser enteros. Para cada uno\(m \in \mathbb{N}\), si\(a \equiv b\) (mod\(n\)), luego\(a^m \equiv b^m\) (mod\(n\)).
- Utilice la inducción matemática para demostrar que la suma de los cubos de tres números naturales consecutivos cualquiera es un múltiplo de 9.
- \(a\)Déjese ser un número real. Exploraremos las derivadas de la función\(f(x) = e^{ax}\). Al usar la regla de la cadena, vemos que
\[\dfrac{d}{dx}(e^{ax}) = ae^{ax}.\]
Recordemos que la segunda derivada de una función es la derivada de la función derivada. De igual manera, la tercera derivada es la derivada de la segunda derivada.
a) ¿Qué es\(\dfrac{d^2}{dx^2}(e^{ax})\), la segunda derivada de\(e^{ax}\)?
b) ¿Qué es\(\dfrac{d^3}{dx^3}(e^{ax})\), el tercer derivado de\(e^{ax}\)?
(c)\(n\) Sea un número natural. Hacer una conjetura sobre las derivadas\(n\) th de la función\(f(x) = e^{ax}\). Es decir, ¿qué es\(\dfrac{d^n}{dx^n}(e^{ax})\)? Esta conjetura debe escribirse como una proposición autónoma que incluya un cuantificador apropiado.
(d) Utilizar la inducción matemática para demostrar que su conjetura. - En el cálculo, se puede demostrar que
\[\begin{array} {lll} {\int sin^2 x dx} &= & {\dfrac{x}{2} - \dfrac{1}{2} sinx cosx + c \ \ \text{and}} \\ {\int cos^2 x dx} &= & {\dfrac{x}{2} + \dfrac{1}{2} sinx cosx + c.}\end{array}\]
Usando la integración por partes, también es posible probar que para cada número natural\(n\),
\[\begin{array} {lll} {\int sin^n x dx} &= & {-\dfrac{1}{n} sin^{n - 1} x cosx + \dfrac{n - 1}{n} \int sin^{n - 2} x dx \ \ \text{and}} \\ {\int cos^n x dx} &= & {\dfrac{1}{n} cos^{n - 1} x sinx + \dfrac{n - 1}{n} \int cos^{n - 2} x dx.}\end{array}\]
(a) Determinar los valores de
\[\int_{0}^{\pi /2} sin^2 x dx \ \ \ \text{and} \ \ \ \int_{0}^{\pi /2} sin^4 x dx.\]
(b) Utilizar la inducción matemática para demostrar que para cada número\(n\)
\[\begin{array} {lll} {\int_{0}^{\pi /2} sin^{2n} x dx} &= & {\dfrac{1 \cdot 3 \cdot 5 \cdot\cdot\cdot (2n - 1)}{2 \cdot 4 \cdot 6 \cdot\cdot\cdot (2n)}\dfrac{\pi}{2} \ \ \ \text{and}} \\ {\int_{0}^{\pi /2} sin^{2n + 1} x dx} &= & \dfrac{2 \cdot 4 \cdot 6 \cdot\cdot\cdot (2n)}{1 \cdot 3 \cdot 5 \cdot\cdot\cdot (2n + 1).} \end{array}\]
natural se conocen como las fórmulas sinusoidales Wallis.
(c) Utilizar la inducción matemática para probar que
\[\begin{array} {lll} {\int_{0}^{\pi /2} cos^{2n} x dx} &= & {\dfrac{1 \cdot 3 \cdot 5 \cdot\cdot\cdot (2n - 1)}{2 \cdot 4 \cdot 6 \cdot\cdot\cdot (2n)}\dfrac{\pi}{2} \ \ \ \text{and}} \\ {\int_{0}^{\pi /2} cos^{2n + 1} x dx} &= & \dfrac{2 \cdot 4 \cdot 6 \cdot\cdot\cdot (2n)}{1 \cdot 3 \cdot 5 \cdot\cdot\cdot (2n + 1).} \end{array}\]
se conocen como las fórmulas coseno de Wallis. - a) ¿Por qué no es posible utilizar la inducción matemática para probar una proposición de la forma
\[(\forall x \in \mathbb{Q}) (P(x)),\]
donde\(P(x)\) hay algún predicado?
(b) ¿Por qué no es posible utilizar la inducción matemática para probar una proposición de la forma
Para cada número real\(x\) con\(x \ge 1\)\(P(x)\),,
donde\ (P (x) es algún predicado? - Evaluación de pruebas
Consulte las instrucciones para Ejercicio (19) en la página 100 de la Sección 3.1.Por cada número natural\(n\),\(1 + 4 + 7 + \cdot\cdot\cdot + (3n - 2) = \dfrac{n(3n -1)}{2}.\)
- Prueba
-
Demostraremos esta proposición mediante inducción matemática. Entonces dejamos que\(P(n)\) sea la frase abierta
\(1 + 4 + 7 + \cdot\cdot\cdot + (3n - 2).\)
Usando\(n= 1\), vemos taht\(3n - 2 = 1\) y por lo tanto,\(P(1)\) es cierto.
Ahora asumimos que taht\(P(k)\) es cierto. Es decir,
\(1 + 4 + 7 + \cdot\cdot\cdot + (3k - 2) = \dfrac{k(3k - 1)}{2}.\)
Entonces vemos que
\[\begin{array} {rcc} {1 + 4 + 7 + \cdot\cdot\cdot + (3k - 2) + (3(k + 1) - 2)} &= & {\dfrac{(k+1)(3k + 2)}{2}} \\ {\dfrac{k(3k - 1)}{2} + (3k + 1)} &= & {\dfrac{(k+1)(3k + 2)}{2}} \\ {\dfrac{(3k^2 - k) + (6k + 2)}{2}} &= & {\dfrac{3k^2 + 5k + 2}{2}} \\ {\dfrac{3k^2 + 5k + 2}{2}} &= & {\dfrac{3k^2 + 5k + 2}{2}}.\end{array}\]
Hemos demostrado así que eso\(P(k+1)\) es cierto, y de ahí, hemos probado la proposición.
Por cada número natural\(n\),\(1 + 4 + 7 + \cdot\cdot\cdot + (3n - 2) = \dfrac{n(3n -1)}{2}.\)
- Prueba
-
Demostraremos esta proposición mediante inducción matemática. Así que dejamos
\(P(n) = 1 + 4 + 7 + \cdot\cdot\cdot + (3n - 2)\).
Usando\(n = 1\), vemos eso\(P(1) = 1\) y por lo tanto,\(P(1)\) es cierto.
Ahora asumimos que eso\(P(k)\) es cierto. Es decir,
\(1 + 4 + 7 + \cdot\cdot\cdot + (3k - 2) = \dfrac{k(3k - 1)}{2}.\)
Entonces vemos que
\[\begin{array} {lcl} {P(k + 1)} &= & {1 + 4 + 7 + \cdot\cdot\cdot + (3k - 2) + (3(k + 1) - 2)} \\ {} &= & {\dfrac{k(3k - 2)}{2} + 3(k + 1) - 2} \\ {} &= & {\dfrac{3k^2 - k + 6k + 6 - 4}{2}} \\ {} &= & {\dfrac{3k^2 + 5k + 2}{2}} \\ {} &= & {\dfrac{(k + 1)(3k + 2)}{2}}.\end{array}\]
hemos demostrado así que eso\(P(k + 1)\) es cierto, y de ahí, hemos probado la proposición.
Todos los perros son de la misma raza.
- Prueba
-
Demostraremos esta proposición mediante inducción matemática. Por cada número natural\(n\), dejamos\(P(n)\) ser
Cualquier conjunto de\(n\) perros consiste en su totalidad por perros de la misma raza.
Vamos a demostrar que para cada número natural\(n\),\(P(n)\) es cierto, lo que demostrará que todos los perros son de la misma raza. Un conjunto con un solo perro consiste enteramente en perros de la misma raza y, por lo tanto,\(P(1)\) es cierto.
Entonces dejamos\(k\) ser un número natural y asumimos que eso\(P(k)\) es cierto, es decir, que cada conjunto de\(k\) perros consiste en perros de la misma raza. Ahora considere un conjunto\(D\) de\(k + 1\) perros, donde
\(D = \{d_1, d_2, ..., d_k, d_{k + 1}\}.\)
Si sacamos al perro\(d_1\) del set\(D\), entonces tenemos un conjunto\(D_1\) de\(k\) perros, y usando la suposición que\(P(k)\) es verdad, estos perros deben ser todos de la misma raza. De igual manera, si\(d_{k + 1}\) retiramos del set\(D\), nuevamente tenemos un juego\(D_2\) de\(k\) perros, y estos perros deben ser todos de la misma raza. Ya que\(D = D_1 \cup D_2\), hemos demostrado que todos los perros en\(D\) deben ser de la misma raza.
Esto demuestra que si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto y, de ahí, por inducción matemática, hemos demostrado que para cada número natural\(n\), cualquier conjunto de\(n\) perros consiste enteramente en perros de la misma raza.
Exploraciones y actividades
- La Importancia del Paso Fundamental. La mayor parte del trabajo realizado en la construcción de una prueba por inducción suele ser en probar el paso inductivo. Este fue sin duda el caso en la Proposición 4.2. No obstante, el paso base es una parte esencial de la prueba. Sin ella, la prueba es incompleta. Para ver esto,\(P(n)\) seamos
\[1 + 2 + \cdot\cdot\cdot + n = \dfrac{n^2 + n + 1}{2}.\]
(a) Vamos\(k \in \mathbb{N}\). Complete la siguiente prueba de que si\(P(k)\) es verdad, entonces\(P(k + 1)\) es verdad.
Vamos\(k \in mathbb{N}\). Supongamos que eso\(P(k)\) es cierto. Es decir, asumir que
\[1 + 2 + \cdot\cdot\cdot + k = \dfrac{k^2 + k + 1}{2}.\]
El objetivo es demostrar que eso\(P(k + 1)\) es cierto. Es decir, necesitamos probar que
\[1 + 2 + \cdot\cdot\cdot + k + (k + 1) = \dfrac{(k + 1)^2 + (k + 1) + 1}{2}.\]
Para ello, sumamos\(k + 1\) a ambos lados de la ecuación (4.1.32). Esto da
\[\begin{array} {rcl} {1 + 2 + \cdot\cdot\cdot + k + (k + 1)} &= & {\dfrac{k^2 + k + 1}{2} + (k + 1)} \\ {} &= & {\cdot\cdot\cdot}.\end{array}\]
(b) ¿Es\(P(1)\) verdad? ¿Es\(P(2)\) verdad? ¿Y qué pasa\(P(3)\) con y\(P(4)\)? Explique cómo esto demuestra que el paso base es una parte esencial de una prueba por inducción. - Regiones de un Círculo. Coloca n puntos igualmente espaciados en un círculo y conecta cada par de puntos con la cuerda del círculo determinada por ese par de puntos. Ver Figura 4.1.
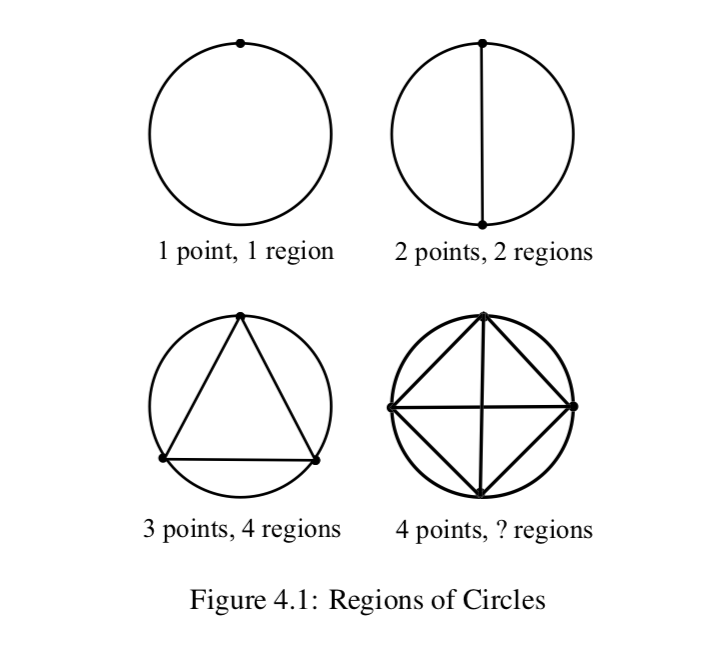
Contar el número de regiones distintas dentro de cada círculo. Por ejemplo, con tres puntos en el círculo, hay cuatro regiones distintas. Organice sus datos en una tabla con dos columnas: “Número de puntos en el círculo” y “Número de regiones distintas en el círculo”.
a) ¿Cuántas regiones hay cuando hay cuatro puntos igualmente espaciados en el círculo?
(b) Basado en el trabajo hasta el momento, haga una conjetura sobre cuántas regiones distintas obtendrías con cinco puntos igualmente espaciados.
(c) Basado en el trabajo hasta el momento, haz una conjetura sobre cuántas regiones distintas obtendrías con seis puntos igualmente espaciados.
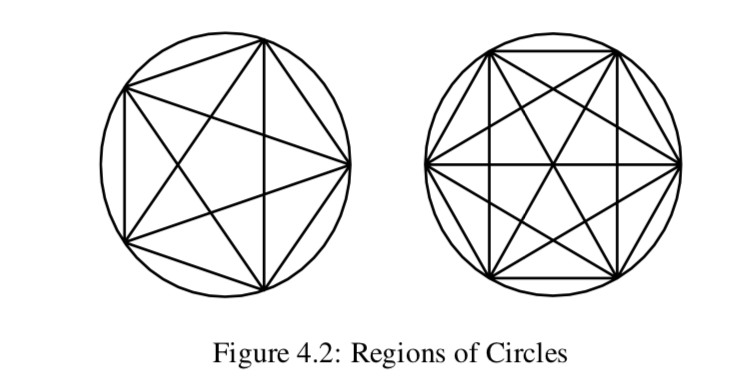
(d) En la Figura 4.2 se muestran las cifras asociadas a las Partes (b) y (c). Contar el número de regiones en cada caso. ¿Tus conjeturas son correctas o incorrectas?
(e) Explicar por qué esta actividad demuestra que el paso inductivo es parte esencial de una prueba por inducción matemática.
- Contestar
-
Agrega textos aquí. No borre primero este texto.


