5.1: Conjuntos y Operaciones en Conjuntos
- Page ID
- 116093
Antes de comenzar esta sección, sería una buena idea revisar conjuntos y notación de conjuntos, incluyendo el método roster y la notación set builder, en la Sección 2.3.
En la Sección 2.1, utilizamos operadores lógicos (conjunción, disyunción, negación) para formar nuevas declaraciones a partir de declaraciones existentes. De manera similar, hay varias formas de crear nuevos conjuntos a partir de conjuntos que ya se han definido. De hecho, formaremos estos nuevos conjuntos usando los operadores lógicos de conjunción (y), disyunción (o) y negación (no). Por ejemplo, si el conjunto universal es el conjunto de números naturales\(N\) y
\[A = \{1, 2, 3, 4, 5, 6\} \quad \text{ and } \quad B = \{1, 3, 5, 7, 9\},\]
- El conjunto que consiste en todos los números naturales que están en\(A\) y están en\(B\) es el conjunto\(\{1, 3, 5\}\);
- El conjunto que consiste en todos los números naturales que están en\(A\) o están en\(B\) es el conjunto\(\{1, 2, 3, 4, 5, 6, 7, 9\}\); y
- El conjunto que consiste en todos los números naturales que están en\(A\) y no están en\(B\) es el conjunto\(\{2, 4, 6\}.\)
Estos conjuntos son ejemplos de algunas de las operaciones de conjuntos más comunes, que se dan en las siguientes definiciones.
Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\). La intersección de\(A\) y\(B\), escrito\(A \cap B\) y leído “\(A\)intersectar”\(B\), es el conjunto de todos los elementos que se encuentran en ambos\(A\) y\(B\). Es decir,
\[A \cap B = \{x \in U \, | \, x \in A \text{ and } x \in B\}.\]
La unión de\(A\) y\(B\), escrita\(A \cup B\) y leída “\(A\)unión”\(B\), es el conjunto de todos los elementos que están en\(A\) o en\(B\). Es decir,
\[A \cup B = \{x \in U \, | \, x \in A \text{ or } x \in B\}.\]
Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\). La diferencia establecida de\(A\) y\(B\), o complemento relativo de\(B\) con respecto a\(A\), escrito\(A -B\) y leído “\(A\)menos\(B\)” o “el complemento de\(B\) con respecto a”\(A\), es el conjunto de todos los elementos en \(A\)que no están en\(B\). Es decir,
\[A - B = \{x \in U \, | \, x \in A \text{ and } x \notin B\}.\]
El complemento del conjunto\(A\), escrito\(A^c\) y leído “el complemento de”\(A\), es el conjunto de todos los elementos de los\(U\) que no están en\(A\). Es decir,
\[A^c = \{x \in U \, | \, x \notin A\}.\]
Para el resto de esta actividad de previsualización, el conjunto universal es\(U = \{0, 1, 2, 3, ..., 10\}\), y usaremos los siguientes subconjuntos de\(U\):
\[A = \{0, 1, 2, 3, 9\} \quad \text{ and } \quad B = \{2, 3, 4, 5, 6\},\]
Entonces en este caso,\(A \cap B = \{x \in U \, | \, x \in A \text{ and } x \in B\} = \{2, 3\}.\) Usa el método roster para especificar cada uno de los siguientes subconjuntos de\(U\).
- \(A \cup B\)
- \(A^c\)
- \(B^c\)
Ahora podemos usar estos conjuntos para formar aún más conjuntos. Por ejemplo,
\[A \cap B^c = \{0, 1, 2, 3, 9\} \cap \{0, 1, 7, 8, 9, 10\} = \{0, 1, 9\}.\]
Utilice el método roster para especificar cada uno de los siguientes subconjuntos de\(U\).
- \(A \cup B^c\)
- \(A^c \cap B^c\)
- \(A^c \cup B^c\)
- \((A \cap B)^c\)
En Preview Activity\(\PageIndex{1}\), se trabajó con definiciones verbales y simbólicas de operaciones de conjunto. Sin embargo, también es útil tener una representación visual de conjuntos. Los diagramas de Venn se utilizan para representar conjuntos mediante círculos (o alguna otra forma geométrica cerrada) dibujados dentro de un rectángulo. Los puntos dentro del rectángulo representan el conjunto universal\(U\), y los elementos de un conjunto están representados por los puntos dentro del círculo que representa el conjunto. Por ejemplo, Figura\(\PageIndex{1}\) es un diagrama de Venn que muestra dos conjuntos.
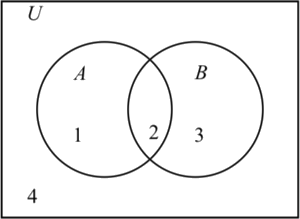
Figura\(\PageIndex{1}\): Diagrama de Venn para dos juegos
En la Figura\(\PageIndex{1}\), los elementos de\(A\) están representados por los puntos dentro del círculo izquierdo, y los elementos de\(B\) están representados por los puntos dentro del círculo derecho. Las cuatro regiones distintas del diagrama están numeradas solo para fines de referencia. (Los números no representan elementos en un conjunto.) En la siguiente tabla se describen las cuatro regiones del diagrama.
| Región | Elementos de\(U\) | Set |
|---|---|---|
| 1 | \ (U\) ">En\(A\) y no en\(B\) | \(A - B\) |
| 2 | \ (U\) ">En\(A\) y en\(B\) | \(A \cap B\) |
| 3 | \ (U\) ">En\(B\) y no en\(A\) | \(B - A\) |
| 4 | \ (U\) ">No en\(A\) y no en\(B\) | \(A^c \cap B^c\) |
Podemos usar estas regiones para representar otros conjuntos. Por ejemplo, el conjunto\(A \cup B\) está representado por las regiones 1, 2 y 3 o la región sombreada en la Figura\(\PageIndex{2}\).
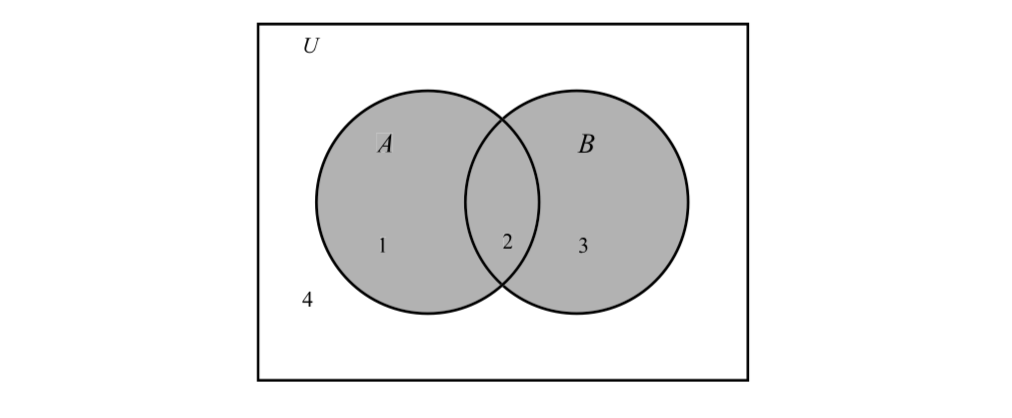
Figura\(\PageIndex{2}\): Diagrama de Venn para\(A \cup B\)
Dejar\(A\) y\(B\) ser subconjuntos de un conjunto universal\(U\). Para cada uno de los siguientes, dibuje un diagrama de Venn para dos conjuntos y sombree la región que representa el conjunto especificado. Además, describa el conjunto usando la notación del constructor de conjuntos.
- \(A^c\)
- \(B^c\)
- \(A^c \cup B\)
- \(A^c \cup B^c\)
- \((A \cap B)^c\)
- \((A \cup B) - (A \cap B)\)
Establecer igualdad, subconjuntos y subconjuntos adecuados
En la Sección 2.3, introdujimos algunas definiciones básicas utilizadas en la teoría de conjuntos, lo que significa decir que dos conjuntos son iguales y lo que significa decir que un conjunto es un subconjunto de otro conjunto. Necesitamos una definición más.
Dejar\(A\) y\(B\) ser dos conjuntos contenidos en algún conjunto universal\(U\). El conjunto\(A\) es un subconjunto apropiado de\(B\) siempre que\(A \subseteq B\) y\(A \ne B\). Cuando\(A\) es un subconjunto adecuado de\(B\), escribimos\(A \subset B\).
Una razón para la definición de subconjunto apropiado es que cada conjunto es un subconjunto de sí mismo. Es decir,
Si\(A\) es un conjunto, entonces\(A \subseteq A\)
Sin embargo, a veces necesitamos indicar que un conjunto\(X\) es un subconjunto de\(Y\) pero\(X \ne Y\). Por ejemplo, si
\(X = \{1, 2\}\)y\(Y = \{0, 1, 2, 3\}.\)
entonces\(X \subset Y\). Sabemos que\(X \subseteq Y\) ya que cada elemento de\(X\) es un elemento de\(Y\), pero\(X \ne Y\) desde\(0 \in Y\) y\(0 \notin X\). (También,\(3 \in Y\) y\(3 \notin X\).) Observe que las notaciones\(A \subset B\) y\(A \subseteq B\) se utilizan de manera similar a la notación de desigualdad para los números (\(a < b\)y\(a \le b\)).
A menudo es muy importante poder describir con precisión lo que significa decir que un conjunto no es un subconjunto del otro. En el ejemplo anterior, no\(Y\) es un subconjunto de\(X\) ya que existe un elemento de\(Y\) (es decir, 0) que no está en\(X\).
En general, la relación de subconjunto se describe con el uso de un cuantificador universal ya que\(A \subseteq B\) significa que para cada elemento\(x\) de\(U\), si\(x \in A\), entonces\(x \in B\). Entonces, cuando negamos esto, usamos un cuantificador existencial de la siguiente manera:
\[\begin{array} {rcl} {A \subseteq B} &\text{means} & {(\forall x \in U)[(x \in A) \to (x \in B)].} \\ {A \not\subseteq B} &\text{means} & {\urcorner(\forall x \in U)[(x \in A) \to (x \in B)]} \\ {} & & {(\exists x \in U) \urcorner [(x \in A) \to (x \in B)]} \\ {} & & {(\exists x \in U) [(x \in A) \wedge (x \notin B)].} \end{array}\]
Entonces vemos que eso\(A \not\subseteq B\) significa que existe una\(x\) en\(U\) tal que\(x \in A\) y\(x \notin B\).
Observe que si\(A = \emptyset\), entonces la declaración condicional, “Para cada uno\(x \in U\), si\(x \in \emptyset\), entonces\(x \in B\)” debe ser verdadera ya que la hipótesis siempre será falsa. Otra forma de ver esto es considerar la siguiente afirmación:
\(\emptyset \not\subseteq B\)significa que existe\(x \in \emptyset\) tal que\(x \notin B\).
No obstante, esta afirmación debe ser falsa ya que no existe un\(x\) in\(\emptyset\). Como esto es falso, debemos concluirlo\(\emptyset \subseteq B\). Si bien los hechos que\(\emptyset \subseteq B\) y\(B \subseteq B\) pueden no parecer muy importantes, los usaremos más adelante, y de ahí los resumiremos en el Teorema 5.1.
Para cualquier conjunto\(B\),\(\emptyset \subseteq B\) y\(B \subseteq B\).
En la Sección 2.3, también definimos dos conjuntos para que sean iguales cuando tienen precisamente los mismos elementos. Por ejemplo,
\(\{x \in \mathbb{R} \, | \, x^ = 4\} = \{-2, 2\}\).
Si los dos conjuntos\(A\) y\(B\) son iguales, entonces debe ser cierto que cada elemento de\(A\) es un elemento de\(B\), es decir,\(A \subseteq B\), y debe ser cierto que cada elemento de\(B\) es un elemento de\(A\), esto es,\(B \subseteq A\). Por el contrario, si\(A \subseteq B\) y\(B \subseteq A\), entonces\(A\) y\(B\) debe tener precisamente los mismos elementos. Esto nos da la siguiente prueba para establecer la igualdad:
Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\). Entonces\(A = B\) si y sólo si\(A \subseteq B\) y\(B \subseteq A\).
Deja que el conjunto universal sea\(U = \{1, 2, 3, 4, 5, 6\}\), y deja que
\(A = \{1, 2, 4\}\),\(B = \{1, 2, 3, 5\}\),\(C = \{x \in U \, | \, x^2 \le 2\}\).
En cada una de las siguientes, rellene el espacio en blanco con uno o más de los símbolos\(\subset\)\(\subseteq\),, =\(\ne\),\(\in\) o\(\notin\) para que la declaración resultante sea verdadera. Por cada espacio en blanco, incluya todos los símbolos que den como resultado una declaración verdadera. Si ninguno de estos símbolos hace una declaración verdadera, no escriba nada en el espacio en blanco.
\[\begin{array} {rclrcl} {A} &\text{_____________} & {B\quad \quad \quad } {\emptyset} &\text{_____________}& {A} \\ {5} &\text{_____________} & {B\quad \quad \ \ \ } {\{5\}} &\text{_____________} & {B} \\ {A} &\text{_____________} & {C\quad \ \ \ \ \ \ } {\{1, 2\}} &\text{_____________} & {C} \\ {\{1, 2\}} &\text{_____________} & {A\quad \ \ \ } {\{4, 2, 1\}} &\text{_____________} & {A} \\ {6} &\text{_____________} & {A\quad \quad \quad } {B} &\text{_____________} & {\emptyset} \end{array} \nonumber\]
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Más sobre Venn Diagramas
En Preview Activity\(\PageIndex{2}\), aprendimos a usar diagramas de Venn como representación visual para conjuntos, operaciones de conjuntos y relaciones de conjuntos. En esa actividad de previsualización, nos limitamos a usar dos sets. Podemos, por supuesto, incluir más de dos conjuntos en un diagrama de Venn. La figura\(\PageIndex{3}\) muestra un diagrama general de Venn para tres conjuntos (incluyendo una región sombreada que corresponde a\(A \cap C\)).
En este diagrama, hay ocho regiones distintas, y cada región tiene un número de referencia único. Por ejemplo, el conjunto A está representado por la combinación de las regiones 1, 2, 4 y 5, mientras que el conjunto C está representado por la combinación de las regiones 4, 5, 6 y 7. Esto significa que el conjunto\(A \cap C\) está representado por la combinación de las regiones 4 y 5. Esto se muestra como la región sombreada en la Figura\(\PageIndex{3}\).
Finalmente, los diagramas de Venn también se pueden utilizar para ilustrar las relaciones especiales entre conjuntos. Por ejemplo, si\(A \subseteq B\), entonces el círculo que representa\(A\) debe estar completamente contenido en el círculo para\(B\). Entonces si\(A \subseteq B\), y no sabemos nada de
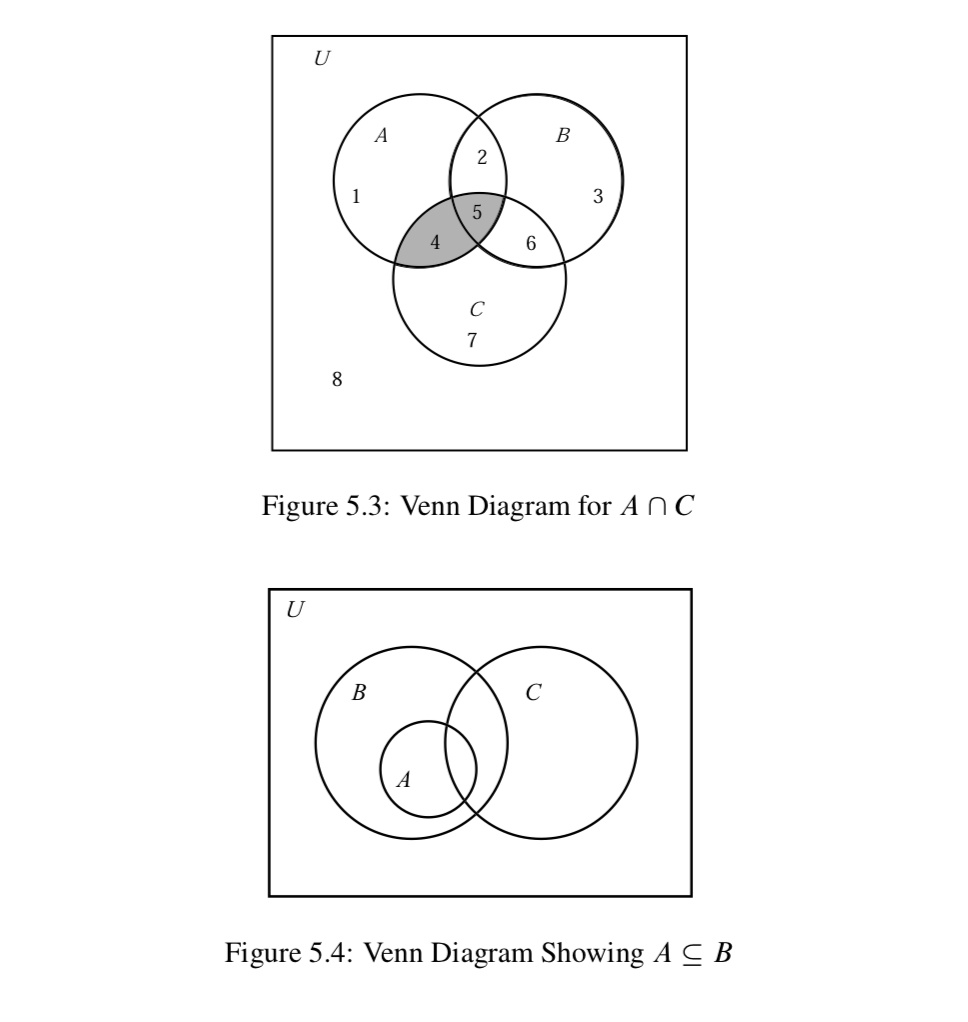
cualquier relación entre el conjunto\(C\) y los conjuntos\(A\) y\(B\), podríamos usar el diagrama de Venn que se muestra en la Figura\(\PageIndex{4}\).
Dejar\(A\),\(B\), y\(C\) ser subconjuntos de un conjunto universal\(U\).
- Para cada uno de los siguientes, dibuje un diagrama de Venn para tres conjuntos y sombree las regiones que representan el conjunto especificado.
a)\((A \cap B) \cap C\)
b)\((A \cap B) \cup C\)
c)\((A^c \cup B)\)
d)\(A^c \cap (B \cup C)\) - Dibuja el diagrama de Venn más general que muestra\(B \subseteq (A \cup C)\).
- Dibuja el diagrama de Venn más general que muestra\(A \subseteq (B^c \cup C)\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
El conjunto de potencia de un conjunto
El símbolo 2 se utiliza para describir una relación entre un elemento del conjunto universal y un subconjunto del conjunto universal, y el símbolo\(\subseteq\) se usa para describir una relación entre dos subconjuntos del conjunto universal. Por ejemplo, el número 5 es un número entero, y así es apropiado escribir\(5 \in \mathbb{Z}\). No es apropiado, sin embargo, escribir\(5 \subseteq \mathbb{Z}\) ya que 5 no es un conjunto. Es importante distinguir entre 5 y {5}. La diferencia es que 5 es un entero y {5} es un conjunto que consiste en un elemento. En consecuencia, es apropiado escribir\(\{5\} \subseteq \mathbb{Z}\), pero no es apropiado escribir\(\{5\} \in \mathbb{Z}\). La distinción entre estos dos símbolos (5 y {5}) es importante cuando discutimos lo que se llama el conjunto de potencias de un conjunto dado.
Si\(A\) es un subconjunto de un conjunto universal\(U\), entonces el conjunto cuyos miembros son todos los subconjuntos de\(A\) se llama el conjunto de potencia de\(A\). Denotamos el conjunto de poder de\(A\) by\(\mathcal{P}(A)\). Simbólicamente, escribimos
\(\mathcal{P}(A) = \{X \subseteq U \, | \, X \subseteq A\}.\)
Es decir,\(X \in \mathcal{P}(A)\) si y sólo si\(X \subseteq A\).
Al tratar con el conjunto de poder de\(A\), siempre debemos recordar eso\(\emptyset \subseteq A\) y\(A \subseteq A\). Por ejemplo, si\(A = \{a, b\}\), entonces los subconjuntos de\(A\) son
\[\emptyset, \{a\}, \{b\}, \{a,b\}.\]
Podemos escribir esto como
\(\mathcal{P}(A) = \{\emptyset, \{a\}, \{b\}, \{a,b\}\}.\)
Ahora vamos\(B = \{a, b, c\}\). Observe eso\(B = A \cup \{c\}\). Podemos determinar los subconjuntos\(B\) de comenzando con los subconjuntos de\(A\) in (5.1.10). Podemos formar los otros subconjuntos de\(B\) tomando la unión de cada conjunto en (5.1.10) con el conjunto\(\{c\}\). Esto nos da los siguientes subconjuntos de\(B\).
\[\{c\}, \{a, c\}, \{b, c\}, \{a, b, c\}.\]
Entonces los subconjuntos de\(B\) son esos conjuntos en (5.1.10) combinados con esos conjuntos en (5.1.11). Es decir, los subconjuntos de\(B\) son
\[\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a, c\}, \{b, c\}, \{a, b, c\},\]
lo que significa que
\(\mathcal{P}(B) = \{\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.\)
Observe que podríamos escribir
\(\{a, c\} \subseteq B\)o eso\(\{a, c\} \in \mathcal{P}(B)\).
También, observe que\(A\) tiene dos elementos y\(A\) tiene cuatro subconjuntos, y\(B\) tiene tres elementos y\(B\) tiene ocho subconjuntos. Ahora, dejemos\(n\) ser un entero no negativo. El siguiente resultado se puede probar mediante inducción matemática. (Ver Ejercicio 17).)
Dejar\(n\) ser un entero no negativo y dejar\(T\) ser un subconjunto de algún conjunto universal. Si el conjunto\(T\) tiene\(n\) elementos, entonces el conjunto\(T\) tiene\(2^n\) subconjuntos. Es decir,\(\mathcal{P}(T)\) tiene\(2^n\) elementos.
La cardenalidad de un conjunto finito
En nuestra discusión sobre el conjunto de poder, nos preocupaba el número de elementos en un conjunto. De hecho, el número de elementos en un conjunto finito es una característica distintiva del conjunto, por lo que le damos el siguiente nombre.
El número de elementos en un conjunto finito\(A\) se llama cardinalidad de\(A\) y se denota por card (\(A\))
tarjeta (\(\emptyset\)) = 0;
tarjeta ({\(a\),\(b\)}) = 2
tarjeta (\(\mathcal{P}(\{a, b\})\)) = 4
Nota teórica: Existe una manera matemática de distinguir entre conjuntos finitos e infinitos, y hay una manera de definir la cardinalidad de un conjunto infinito. No nos vamos a preocupar por esto en este momento. Más sobre la cardinalidad de los conjuntos finitos e infinitos se discute en el Capítulo 9.
Sistemas de números estándar
Podemos usar la notación de conjunto para especificar y ayudar a describir nuestros sistemas numéricos estándar. El punto de partida es el conjunto de números naturales, para lo cual utilizamos el método roster.
\(\mathbb{N} = \{1, 2, 3, 4, ...\}\)
Los números enteros consisten en los números naturales, los negativos de los números naturales y cero. Si lo dejamos\(\mathbb{N} ^- = \{..., -4, -3, -2, -1\}\), entonces podemos usar set union y escribir
\(\mathbb{Z} = \mathbb{N} ^- \cup \{0\} \cup \mathbb{N}\).
Entonces vemos eso\(\mathbb{N} \subseteq \mathbb{Z}\), y de hecho,\(\mathbb{N} \subset \mathbb{Z}\).
Necesitamos usar la notación set builder para el conjunto\(\mathbb{Q}\) de todos los números racionales, que consiste en cocientes de enteros.
\(\mathbb{Q} = \Big\{\dfrac{m}{n}\ |\ m, n \in \mathbb{Z} \text{and } n \ne 0\Big\}\)
Dado que cualquier entero se\(n\) puede escribir como\(n = \dfrac{n}{1}\), vemos que\(\mathbb{Z} \subseteq \mathbb{Q}\).
Aún no contamos con las herramientas para dar una descripción completa de los números reales. Simplemente diremos que los números reales consisten en los números racionales y los números irracionales. En efecto, los números irracionales son el complemento del conjunto de números racionales\(\mathbb{Q}\) en\(\mathbb{R}\). Así podemos usar la notación\(\mathbb{Q} ^c = \{x \in \mathbb{R}\ |\ x \notin \mathbb{Q}\}\) y escribir
\(\mathbb{R} = \mathbb{Q} \cup \mathbb{Q} ^c\)y\(\mathbb{Q} \cap \mathbb{Q} ^c = \emptyset\).
Un sistema numérico que aún no hemos discutido es el conjunto de números complejos. Los números complejos,\(\mathbb{C}\), constan de todos los números de la forma\(a + bi\), donde\(a, b \in \mathbb{R}\) y\(i = \sqrt{-1}\) (o\(i^2 = -1\)). Es decir,
\(\mathbb{C} = \{a + bi\ |\ a,b \in \mathbb{R} \text{and } i = sqrt{-1}\}.\)
Podemos sumar y multiplicar números complejos de la siguiente manera: Si\(a, b, c, d \in \mathbb{R}\), entonces
\[\begin{array} {rcl} {(a + bi) + (c + di)} &= & {(a + c) + (b + d)i, \text{ and}} \\ {(a + bi)(c + di)} &= & {ac + adi + bci + bdi^2} \\ {} &= & {(ac - bd) + (ad + bc)i.} \end{array}\]
- Supongamos que el conjunto universal es el conjunto de números reales. Deja
\(A = \{-3, -2, 2, 3\}.\)
\(B = \{x \in \mathbb{R}\ |\ x^2 = 4 \text{ or } x^2 = 9\},\)
\(C = \{x \in \mathbb{R}\ |\ x^2 + 2 = 0\},\)
\(D = \{x \in \mathbb{R}\ |\ x > 0\}.\)
Responder a cada una de las siguientes preguntas. En cada caso, explique su respuesta.
(a) ¿El conjunto es\(A\) igual al conjunto\(B\)?
b) ¿El conjunto es\(A\) un subconjunto del conjunto\(B\)?
(c) ¿El conjunto es\(C\) igual al conjunto\(D\)?
d) ¿El conjunto es\(C\) un subconjunto del conjunto\(D\)?
e) ¿El conjunto es\(A\) un subconjunto del conjunto\(D\)? - (a) Explique por qué el conjunto\(\{a, b\}\) es igual al conjunto\(\{b, a\}\).
b) Explicar por qué el conjunto\(\{a, b, b, a, c\}\) es igual al conjunto\(\{b, c, a\}\). - Supongamos que el conjunto universal es el conjunto de enteros. Deje
\(A = \{-3, -2, 2, 3\}.\)
\(B = \{x \in \mathbb{Z}\ |\ x^2 \le 9\},\)
\(C = \{x \in \mathbb{Z}\ |\ x \ge -3\},\)
\(D = \{1, 2, 3, 4\},\)
En cada una de las siguientes, rellene el espacio en blanco con uno o más de los símbolos\(\subset\),\(\subseteq\),\(\not\subseteq\), \(=\)\(\ne\),\(\in\) o\(\notin\) para que la afirmación resultante sea cierta. Por cada espacio en blanco, incluya todos los símbolos que den como resultado una declaración verdadera. Si ninguno de estos símbolos hace una declaración verdadera, no escriba nada en el espacio en blanco.
\[\begin{array} {rclrcl} {A} &\text{_____________} & {B\quad \quad \quad \ \ \ \ \ } {\emptyset} &\text{_____________}& {A} \\ {5} &\text{_____________} & {C\quad \quad \quad \ \ } {\{5\}} &\text{_____________} & {C} \\ {A} &\text{_____________} & {C\quad \quad \ \ \ \ \ } {\{1, 2\}} &\text{_____________} & {B} \\ {\{1, 2\}} &\text{_____________} & {A\quad \quad \ \ } {\{3, 2, 1\}} &\text{_____________} & {D} \\ {4} &\text{_____________} & {B\quad \quad \quad \ \ \ \ \ } {D} &\text{_____________} & {\emptyset} \\ {\text{card} (A)} &\text{_____________} & {\text{card} (D)\quad \ } {\text{card} (A)} &\text{_____________} & {\text{card} (B)} \\ {A} &\text{_____________} & {\mathcal{P}(A)\quad \quad \quad } {A} &\text{_____________} & {\mathcal {P} (B)} \end{array}\] - Escriba todas las relaciones de subconjunto adecuadas que sean posibles usando los conjuntos de números\(\mathbb{N}\),\(\mathbb{Z}\),\(\mathbb{Q}\), y\(\mathbb{R}\).
- Para cada enunciado, escriba una explicación breve y clara de por qué la afirmación es verdadera o por qué es falsa.
(a) El conjunto\(\{a, b\}\) es un subconjunto de\(\{a, c, d, e\}\).
(b) El conjunto\(\{-2, 0, 2\}\) es igual a\(\{x \in \mathbb{Z} \, | \, x\) es par y\(x^2 < 5\}.\)
(c) El conjunto vacío\(\emptyset\) es un subconjunto de\(\{1\}.\)
(d) Si\(A = \{a, b\}\), entonces el conjunto\(\{a\}\) es un subconjunto de\(\mathcal{P} (A)\). - Utilice las definiciones de intersección de conjunto, unión de conjuntos y diferencia de conjunto para escribir negaciones útiles de estas definiciones. Es decir, completar cada una de las siguientes frases
(a)\(x \notin A \cap B\) si y sólo si....
b)\(x \notin A \cup B\) si y sólo si....
c)\(x \notin A - B\) si y sólo si.... - Dejar\(U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\},\) y dejar
\(A = \{3, 4, 5, 6, 7\}\)
\(B = \{1, 5, 7, 9\}\)
\(C = \{3, 6, 9\}\)
\(D = \{2, 4, 6, 8\}\)Utilice el método roster para enumerar todos los elementos de cada uno de los siguientes conjuntos.
(a)\(A \cap B\)
(b)\(A \cup B\)
(c)\((A \cup B)^c\)
(d)\(A^c \cap B^c\)
(e)\((A \cup B) \cap C\)
(f)\(A \cap C\)
(g)\(B \cap C\)
(h)\((A \cap C) \cup (B \cap C)\)
(i) \(B \cap D\)
(j)\((B \cap D)^c\)
(k)\(A - D\)
(l)\(B - D\)
(m)\((A - D) \cup (B - D)\)
(n)\((A \cup B) - D\) - Let\(U = \mathbb{N}\), y let
\(A =\{x \in \mathbb{N}\ |\ x \ge 7\},\)
\(B =\{x \in \mathbb{N}\ |\ x \text{ is odd}\},\)
\(C =\{x \in \mathbb{N}\ |\ x \text{ is a multiple of } 3\},\)
\(D =\{x \in \mathbb{N}\ |\ x \text{ is even}\},\)
Use el método roster para enumerar todos los elementos de cada uno de los siguientes conjuntos.
(a)\(A \cap B\)
(b)\(A \cup B\)
(c)\((A \cup B)^c\)
(d)\(A^c \cap B^c\)
(e)\((A \cup B) \cap C\)
(f)\((A \cap C) \cup (B \cap C)\)
(g)\(B \cap D\)
(h) \((B \cap D)^c\)
i\(A - D\)
) j\(B - D\)
) k\((A - D) \cup (B - D)\)
) l)\((A \cup B) - D\) - let\(P\),\(Q\),\(R\), y\(S\), ser subconjuntos de un conjunto universal\(U\), Supongamos que\((P - Q) \subseteq (R \cap S)\).
a) Completar la siguiente frase:
Para cada uno\(x \in U\), si\(x \in (P - Q)\), entonces....
(b) Escribir una negación útil de la declaración en la Parte (9a).
(c) Escribir el contrapositivo de la declaración en la Parte (9a). - \(U\)Déjese ser el conjunto universal. Considere la siguiente declaración:
Para todos\(A\),\(B\), y\(C\) que son subconjuntos de\(U\), si\(A \subseteq B\), entonces\(B^c \subseteq A^c\).
a) Identificar tres declaraciones condicionales en el enunciado dado.
b) Escribir el contrapositivo de esta declaración.
c) Escribir la negación de esta afirmación. - Dejar\(A\),\(B\), y\(C\) ser subconjuntos de algunos conjuntos universales\(U\). Dibuja un diagrama de Venn para cada una de las siguientes situaciones.
(a)\(A \subseteq C\)
(b)\(A \cap B = \emptyset\)
(c)\(A \not\subseteq B\)\(B \not\subseteq A\),\(C \subseteq A\),, y\(C \not\subseteq B\)
(d)\(A \subseteq B\)\(C \subseteq B\), y\(A \cap C = \emptyset\) - Dejar\(A\),\(B\), y\(C\) ser subconjuntos de algunos conjuntos universales\(U\). Para cada uno de los siguientes, dibuje un diagrama general de Venn para los tres conjuntos y luego sombree la región indicada.
a)\(A \cap B\)
b\(A \cap C\)
) c\((A \cap B) \cup (A \cap C)\)
) d\(B \cup C\)
) e\(A \cap (B \cup C)\)
) f\((A \cap B) - C\) - Podemos extender la idea de enteros consecutivos (Ver Ejercicio (2) en la Sección 3.5) para representar cuatro enteros consecutivos como\(m\),\(m + 1\),\(m + 2\), y\(m + 3\), donde\(m\) es un entero. Hay otras formas de representar cuatro enteros consecutivos. Por ejemplo, si\(k \in \mathbb{Z}\), entonces\(k - 1\)\(k\),\(k + 1\),, y\(k + 2\) son cuatro enteros consecutivos.
(a) Demostrar que para cada uno\(n \in \mathbb{Z}\),\(n\) es la suma de cuatro enteros consecutivos si y sólo si\(n \equiv 2\) (mod 4).
(b) Utilice la notación de generador de conjuntos o el método roster para especificar el conjunto de enteros que son la suma de cuatro enteros consecutivos.
(c) Especificar el conjunto de todos los números naturales que pueden escribirse como la suma de cuatro números naturales consecutivos.
(d) Demostrar que para cada uno\(n \in \mathbb{Z}\),\(n\) es la suma de ocho enteros consecutivos si y sólo si\(n \equiv 4\) (mod 8).
(e) Utilice la notación de generador de conjuntos o el método roster para especificar el conjunto de enteros que son la suma de ocho enteros consecutivos.
(f) Especificar el conjunto de todos los números naturales se puede escribir como la suma de ocho números naturales consecutivos. - Una de las propiedades de los números reales es la llamada Ley de la Tricotomía, que establece que si\(a, b \in \mathbb{R}\), entonces exactamente una de las siguientes es cierta:
- \(a < b\);
- \(a = b\);
- \(a > b\).
¿La siguiente proposición relativa a conjuntos es verdadera o falsa? O bien proporcionar una prueba de que es cierto o un contraejemplo que demuestre que es falso.
Si A y B son subconjuntos de algún conjunto universal, entonces es cierto exactamente uno de los siguientes: - \(A \subseteq B\);
- \(A = B\);
- \(B \subseteq A\).
Exploraciones y actividades
15. Intervalos de Números Reales. En cursos previos de matemáticas, hemos utilizado frecuentemente subconjuntos de los números reales llamados intervalos. Hay algunos nombres y anotaciones comunes para intervalos. Estos se dan en la siguiente tabla, donde se supone que a y b son números reales y\(a < b\).
| Notación de intervalos | Notación de conjunto | Nombre |
| (\(a\),\(b\)) = | {\(x \in \mathbb{R} \, | \, a < x < b\)} | Intervalo abierto de\(a\) a\(b\) |
| [\(a\),\(b\)] = | {\(x \in \mathbb{R} \, | \, a \le x \le b\)} | Intervalo cerrado de\(a\) a\(b\) |
| [\(a\),\(b\)) = | {\(x \in \mathbb{R} \, | \, a \le x < b\)} | Intervalo medio abierto |
| (\(a\),\(b\)] = | {\(x \in \mathbb{R} \, | \, a < x \le b\)} | Intervalo medio abierto |
| (\(a\),\(+ \infty\)) = | {\(x \in \mathbb{R} \, | \, x > a\)} | Rayos abiertos |
| (\(- \infty\),\(b\)) = | {\(x \in \mathbb{R} \, | \, x < b\)} | Rayos abiertos |
| [\(a\),\(+ \infty\)) = | {\(x \in \mathbb{R} \, | \, x \ge a\)} | Rayo cerrado |
| (\(- \infty\),\(b\)] = | {\(x \in \mathbb{R} \, | \, x \le b\)} | Rayo cerrado |
(a) ¿Es\((a, \, b)\) un subconjunto apropiado de\((a, \, b]\)? Explique.
b) ¿Es\([a, \, b]\) un subconjunto de\((a, \,+ \infty)\)? Explique.
(c) Usar notación de intervalo para describir
i. la intersección del intervalo\([-3, \, 7]\) con el intervalo\((5, 9];\)
ii. la unión del intervalo\([-3, 7]\) con el intervalo\((5, 9];\)
iii. la diferencia establecida\([-3, 7] - (5, 9].\)
(d) Escribir el conjunto {\(x \in \mathbb{R} \, | \, |x| \le 0.01\)} usando notación de intervalo.
(e) Escribir el conjunto {\(x \in \mathbb{R} \, | \, |x| > 2\)} como la unión de dos intervalos.
16. Más Trabajo con Intervalos. Para este ejercicio, utilice la notación de intervalo descrita en el Ejercicio 15.
(a) Determinar la intersección y unión de\([2, 5]\) y\([-1, \, + \infty).\)
(b) Determinar la intersección y unión de\([2, 5]\) y\([3.4, \, + \infty).\)
(c) Determinar la intersección y unión de\([2, 5]\) y\([7, \, + \infty). \)
Ahora vamos\(a\),\(b\) y\(c\) ser números reales con\(a < b\).
d) Explicar por qué la intersección de\([a, \, b]\) y\([c, \, + \infty)\) es un intervalo cerrado, un conjunto con un elemento, o el conjunto vacío.
(e) Explicar por qué la unión de\([a, \, b]\) y\([c, \,+ \infty)\) es un rayo cerrado o la unión de un intervalo cerrado y un rayo cerrado.
17. Prueba de Teorema 5.5. Para ayudar con la prueba por inducción del Teorema 5.5, primero probamos el siguiente lema. (La idea para la prueba de este lema se ilustró con la discusión del conjunto de poder después de la definición en la página 222.)
Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Si\(A = B \cup \{x\}\), donde\(x \notin B\), entonces cualquier subconjunto de\(A\) es un subconjunto de\(B\) o un conjunto de la forma\(C \cup \{x\}\), donde\(C\) es un subconjunto de\(B\).
- Prueba
-
Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal, y asumir que\(A = B \cup \{x\}\) donde\(x \notin B\). Dejar\(Y\) ser un subconjunto de\(A\). Tenemos que demostrar que\(Y\) es un subconjunto de\(B\) o que\(Y = C \cup \{x\}\), donde\(C\) es algún subconjunto de\(B\). Hay dos casos a considerar: (1) no\(x\) es un elemento de\(Y\), y (2)\(x\) es un elemento de\(Y\).
Caso 1: Supongamos que\(x \notin Y\). Vamos\(y \in Y\). Entonces. \(y \in A\)y\(y \ne x\). Desde
\(A = B \cup \{x\}\),
esto quiere decir que\(y\) debe estar en\(B\). Por lo tanto,\(Y \subseteq B\).
Caso 2: Supongamos que\(x \in Y\). En este caso, vamos\(C = Y - \{x\}\). Entonces cada elemento de\(C\) es un elemento de\(B\). De ahí que podamos concluir eso\(C \subseteq B\) y aquello\(Y = C \cup \{x\}\).
Los casos (1) y (2) muestran que si\(Y \subseteq A\), entonces\(Y \subseteq B\) o\(Y = C \cup \{x\}\), donde\(C \subseteq B\).
Para comenzar la prueba de inducción del Teorema 5.5, para cada entero no negativo\(n\), dejamos\(P(n)\) ser, “Si un conjunto finito tiene exactamente\(n\) elementos, entonces ese conjunto tiene exactamente\(2^n\) subconjuntos”.
a) Verificar que\(P(0)\) sea cierto. (Este es el paso base para la prueba de inducción).
b) Verificar que\(P(1)\) y\(P(2)\) sean ciertos.
(c) Ahora supongamos que\(k\) es un entero no negativo y asumamos que eso\(P(k)\) es cierto. Es decir, supongamos que si un conjunto tiene\(k\) elementos, entonces ese conjunto tiene\(2^k\) subconjuntos. (Esta es la suposición inductiva para la prueba de inducción). Dejar\(T\) ser un subconjunto del conjunto universal con tarjeta\((T) = k + 1\), y dejar\(x \in T\). Entonces el conjunto\(B = T - \{x\}\) tiene\(k\) elementos.
Ahora use la suposición inductiva para determinar cuántos subconjuntos\(B\) tiene. Entonces usa Lemma 5.6 para demostrar que\(T\) tiene el doble de subconjuntos que\(B\). Esto debería ayudar a completar el paso inductivo para la prueba de inducción.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.


