5.2: Demostrar relaciones establecidas

Vista previa de la actividad\(\PageIndex{1}\): Working with Two Specific Sets

Dejar\(S\) ser el conjunto de todos los enteros que son múltiplos de 6, y dejar\(T\) ser el conjunto de todos los enteros pares.

1. Enumere al menos cuatro elementos positivos diferentes de\(S\) y al menos cuatro elementos negativos diferentes de\(S\). ¿Todos estos enteros son parejos?
2. Utilice el método roster para especificar los conjuntos\(S\) y\(T\). (Consulte la Sección 2.3 para una revisión del método de la lista.) ¿Parece haber alguna relación entre estos dos conjuntos? Es decir, ¿parece que los conjuntos son iguales o que un conjunto es un subconjunto del otro conjunto?
3. Utilice la notación del generador de conjuntos para especificar los conjuntos\(S\) y\(T\). (Consulte la Sección 2.3 para una revisión de la notación del constructor de conjuntos.)
4. Usando definiciones apropiadas, describa lo que significa decir que un entero\(x\) es un múltiplo de 6 y lo que significa decir que un entero\(y\) es par.
5. Para probar que\(S\) es un subconjunto de\(T\), necesitamos probarlo para cada entero\(x\), si\(x \in S\), entonces\(x \in T\).
   
   Completar la tabla know show en la Tabla 5.1 para la proposición que\(S\) es un subconjunto de\(T\).
   
   Esta tabla tiene la forma de un método de prueba llamado método de elegir un elemento. Este método se usa frecuentemente cuando encontramos un cuantificador universal en una declaración en el proceso hacia atrás. (En este caso, este es el Paso\(Q\) 1.) La clave es que tenemos que probar algo sobre todos los elementos en\(\mathbb{Z}\). Entonces podemos agregar algo al proceso de reenvío eligiendo un elemento arbitrario del conjunto S. (Esto se hace en el Paso\(P\) 1.) Esto no quiere decir que podamos elegir un elemento específico de\(S\). Más bien, debemos darle un nombre al elemento arbitrario y usar solo las propiedades que tiene al ser miembro del conjunto\(S\). En este caso, el elemento es un múltiplo de 6.

Tabla 5.1: Tabla de saber-mostrar para la Actividad de Vista Previa\(\PageIndex{1}\)

Paso	Conoce	Razón
\(P\)	\(S\)es el conjunto de todos los enteros que son múltiplos de 6. \(T\)es el conjunto de todos los pares. enteros.	Hipótesis
\(P\)1	Vamos\(x \in S\).	Elija un elemento arbitrario de\(S\).
\(P\)2	\((\exists m \in \mathbb{Z})(x = 6m)\)	Definición de “múltiple”
...	...	...
\(Q\)2	\(x\)es un elemento\(T\).	\(x\)es parejo
\(Q\)1	\((\forall x \in \mathbb{Z})[(x \in S) \to (x \in T)]\)	Paso\(P\) 1 y Paso\(Q\) 2
\(Q\)	\(S \subseteq T\).	Definición de “subconjunto”
Paso	Mostrar	Razón

Vista previa de la actividad\(\PageIndex{2}\): Working with Venn Diagrams

1. Dibuja un diagrama de Venn para dos conjuntos,\(A\) y\(B\), con la suposición de que\(A\) es un subconjunto de\(B\). En este diagrama de Venn, sombree ligeramente el área correspondiente a\(A^c\). Después, determinar la región en el diagrama de Venn que corresponde a\(B^c\). ¿Cuál parece ser la relación entre\(A^c\) y\(B^c\)? Explique.
2. Dibuja un diagrama general de Venn para dos conjuntos,\(A\) y\(B\). Primero determinar la región que corresponde al conjunto\(A - B\) y luego, en el diagrama de Venn, sombrear la región correspondiente\(A - (A - B)\) y sombrear la región correspondiente a\(A \cap B\). ¿Cuál parece ser la relación entre estos dos conjuntos? Explique.

En esta sección, aprenderemos a probar ciertas relaciones sobre conjuntos. Dos de los tipos más básicos de relaciones entre conjuntos son la relación de igualdad y la relación de subconjunto. Entonces, si nos hacen una pregunta de la forma, “¿Cómo están los conjuntos\(A\) y\(B\) relacionados?” , podemos responder a la pregunta si podemos probar que los dos conjuntos son iguales o que un conjunto es un subconjunto del otro conjunto. Hay otras formas de responder a esto, pero por ahora nos concentraremos en estas dos. Esto es similar a hacer una pregunta sobre cómo se relacionan dos números reales. Dos números reales se pueden relacionar por el hecho de que son iguales o por el hecho de que un número es menor que el otro número.

El método de elegir un elemento

El método de prueba que usaremos en esta sección se puede llamar el método de elegir un elemento. Este método se introdujo en Preview Activity\(\PageIndex{1}\). Este método se usa frecuentemente cuando encontramos un cuantificador universal en una declaración en el proceso hacia atrás. Esta declaración suele tener la forma

Por cada elemento con una propiedad dada, algo sucede.

Dado que la mayoría de las declaraciones con un cuantificador universal pueden expresarse en forma de declaración condicional, esta afirmación podría tener la siguiente forma equivalente:

Si un elemento tiene una propiedad dada, entonces sucede algo.

Ilustraremos esto con la propuesta de Preview Activity\(\PageIndex{1}\). Esta proposición se puede afirmar de la siguiente manera:

Dejar\(S\) ser el conjunto de todos los enteros que son múltiplos de 6, y dejar\(T\) ser el conjunto de todos los enteros pares. Entonces\(S\) es un subconjunto de\(T\).

En Actividad previa\(\PageIndex{1}\), trabajamos en una mesa de know show para esta propuesta. La clave fue que en el proceso atrasado, nos encontramos con la siguiente afirmación:

Cada elemento de\(S\) es un elemento de\(T\) o, más precisamente, si\(x \in S\), entonces\(x \in T\).

En este caso, el “elemento” es un entero, la “propiedad dada” es que es un elemento de\(S\), y el “algo que sucede” es que el elemento también es un elemento de\(T\). Una forma de abordar esto es crear una lista de todos los elementos con la propiedad dada y verificar que para cada uno, el “algo sucede”. Cuando la lista es corta, este puede ser un enfoque razonable. No obstante, como en este caso, cuando la lista es infinita (o incluso simplemente larga), este enfoque no es práctico.

Superamos esta dificultad utilizando el método de elegir un elemento, donde elegimos un elemento arbitrario con la propiedad dada. Entonces en este caso, elegimos un entero\(x\) que sea un múltiplo de 6. No podemos usar un múltiplo específico de 6 (como 12 o 24), sino que lo único que podemos suponer es que el entero satisface la propiedad de que es un múltiplo de 6. Esta es la parte clave de este método.

Siempre que elegimos un elemento arbitrario con una propiedad dada, no estamos seleccionando un elemento específico. Más bien, lo único que podemos suponer del elemento es la propiedad dada.

Es importante darse cuenta de que una vez que hemos elegido el elemento arbitrario, hemos agregado información al proceso forward. Entonces, en la tabla de know show para esta proposición, agregamos la declaración, “Let\(x \in S\)” al proceso de avance. A continuación se presenta una prueba completa de esta proposición siguiendo el esquema de la tabla de conocimientos de la Actividad previa\(\PageIndex{1}\).

Proposición 5.7

Dejar\(S\) ser el conjunto de todos los enteros que son múltiplos de 6, y dejar\(T\) ser el conjunto de todos los enteros pares. Entonces\(S\) es un subconjunto de\(T\).

Prueba

Dejar\(S\) ser el conjunto de todos los enteros que son múltiplos de 6, y dejar\(T\) ser el conjunto de todos los enteros pares. Mostraremos que\(S\) es un subconjunto de\(T\) mostrando que si un entero x es un elemento de\(S\), entonces también es un elemento de\(T\).

Vamos\(x \in S\). (Nota: El uso de la palabra “dejar” suele ser una indicación de que estamos eligiendo un elemento arbitrario.) Esto significa que x es un múltiplo de 6. Por lo tanto, existe un entero\(m\) tal que

\(x = 6m\).

Ya que\(6 = 2 \cdot 3\), esta ecuación se puede escribir en la forma

\(x = 2(3m)\).

Por propiedades de cierre de los enteros, 3m es un número entero. De ahí que esta última ecuación pruebe que\(x\) debe ser parejo. Por lo tanto, hemos demostrado que si\(x\) es un elemento de\(S\), entonces\(x\) es un elemento de\(T\), y de ahí eso\(S \subseteq T\).

Habiendo demostrado que\(S\) es un subconjunto de\(T\), ahora podemos preguntar si en realidad\(S\) es igual a\(T\). El trabajo que hicimos en Preview Activity\(\PageIndex{1}\) puede ayudarnos a responder a esta pregunta. En esa actividad de previsualización, deberíamos haber encontrado varios elementos que están en\(T\) pero no en\(S\). Por ejemplo, el entero 2 está en\(T\) ya que 2 es par pero\(2 \notin S\) ya que 2 no es un múltiplo de 6. Por lo tanto,\(S \ne T\) y también podemos concluir que\(S\) es un subconjunto propio de\(T\).

Una razón por la que hacemos esto en un proceso de “dos pasos” es que es mucho más fácil trabajar con la relación de subconjunto que con la relación de subconjunto adecuada. La relación de subconjuntos es multada por una declaración condicional y la mayor parte de nuestro trabajo en matemáticas se ocupa de probar declaraciones condicionales. Además, la relación de subconjunto adecuada es una conjunción de dos declaraciones (\(S \subseteq T\)y\(S \ne T\)) y por lo tanto es natural tratar las dos partes de la conjunción por separado.

Comprobación de Progreso 5.8: Subconjuntos e Igualdad de Conjuntos

Dejar\(A = \{x \in \mathbb{Z}\ |\ x \text{ is a multiple of 9}\}\) y dejar\(B = \{x \in \mathbb{Z}\ |\ x \text{ is a multiple of 3}\}\)

1. ¿El conjunto es\(A\) un subconjunto de\(B\)? Justifica tu conclusión.
2. ¿El conjunto es\(A\) igual al conjunto\(B\)? Justifica tu conclusión.

Contestar

Agrega textos aquí. No elimine primero este texto.

Comprobación de progreso 5.9: Uso del método Choose-an-Element

El diagrama de Venn en Preview Activity\(\PageIndex{2}\) sugiere que la siguiente proposición es cierta.

Proposición 5.10.

Dejar\(A\) y\(B\) ser subconjuntos del conjunto universal\(U\). Si\(A \subseteq B\), entonces\(B^c \subseteq A^c\).

1. La conclusión de la declaración condicional es\(B^c \subseteq A^c\). Explique por qué deberíamos probar el método de elegir un elemento para probar esta proposición.
2. Complete la siguiente tabla de conocimientos para esta propuesta y explique exactamente dónde se utiliza el método de elegir un elemento.

Paso	Conoce	Razón
\(P\)	\(A \subseteq B\)	Hipótesis
\(P\)1	Vamos\(x \in B^c\).	Elija un elemento arbitrario de\(B^c\).
\(P\)2	Si\(x \in A\), entonces\(x \in B\).	Definición de “subconjunto”
...	...	...
\(Q\)1	Si\(x \in B^c\), entonces\(x \in A^c\).
\(Q\)	\(B^c \subseteq A^c\)	Definición de “subconjunto”
Paso	Mostrar	Razón

Contestar

Agrega textos aquí. No elimine primero este texto.

Demostrando Conjunto Igualdad

Una forma de probar que dos conjuntos son iguales es usar el Teorema 5.2 y probar que cada uno de los dos conjuntos es un subconjunto del otro conjunto. En particular, que A y B sean subconjuntos de algún conjunto universal. Teorema 5.2 establece que\(A = B\) si y solo si\(A \subseteq B\) y\(B \subseteq A\).

En Preview Activity\(\PageIndex{2}\), creamos un diagrama de Venn que indicaba que\(A - (A - B) = A \cap B\). A continuación se presenta una prueba de este resultado. Observe dónde se usa el método de elegir un elemento en cada caso.

Proposición 5.11.

Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Entonces\(A - (A - B) = A \cap B\).

Prueba

Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Eso lo demostraremos\(A - (A - B) = A \cap B\) demostrando eso\(A - (A - B) \subseteq A \cap B\) y aquello\(A \cap B \subseteq A - (A - B)\).

Primero, vamos\(x \in A - (A - B)\). Esto significa que

\(x \in A\)y\(x \notin (A - B)\).

Sabemos que un elemento está en\((A - B)\) si y sólo si está en\(A\) y no en\(B\). Ya que\(x \notin (A - B)\), concluimos que\(x \notin A\) o\(x \in B\). No obstante, eso también lo sabemos\(x \in A\) y así lo concluimos\(x \in B\). Esto demuestra que

\(x \in A\)y\(x \in B\).

Esto significa eso\(x \in A \cap B\), y de ahí lo hemos demostrado\(A - (A - B) \subseteq A \cap B\).

Ahora elegimos\(y \in A \cap B\). Esto significa que

\(y \in A\)y\(y \in B\).

Observamos que\(y \in (A - B)\) si y sólo si\(y \in A\)\(y \notin B\) y por lo tanto,\(y \notin (A - B)\) si y sólo si\(y \notin A\) o\(y \in B\). Ya que lo hemos probado\(y \in B\), concluimos que\(y \notin (A - B)\), y de ahí, hemos establecido que\(y \in A\) y\(y \notin (A - B)\). Esto demuestra que si\(y \in A \cap B\), entonces\(y \in A - (A - B)\) y por lo tanto,\(A \cap B \subseteq A - (A - B)\).

Ya que lo hemos probado\(A - (A - B) \subseteq A \cap B\) y\(A \cap B \subseteq A - (A - B)\) concluimos que\(A - (A - B) = A \cap B\).

Comprobación de Progreso 5.12: Establecer Igualdad

Demostrar la siguiente proposición. Para ello, pruebe que cada conjunto es un subconjunto del otro conjunto mediante el método de elegir un elemento.

Proposición 5.13.

Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Entonces\(A - B = A \cap B^c\).

Contestar

Agrega textos aquí. No elimine primero este texto.

Conjuntos disarticulares

Anteriormente en esta sección, discutimos el concepto de igualdad de conjunto y la relación de un conjunto siendo un subconjunto de otro conjunto. Hay otras posibles relaciones entre dos conjuntos; uno es que los conjuntos son disjuntos. Básicamente, dos series son disjuntas si y sólo si no tienen nada en común. Esto lo expresamos formalmente en la siguiente definición.

Definición: disjoint

Dejar\(A\) y\(B\) ser subconjuntos del conjunto universal\(U\). Los conjuntos\(A\) y\(B\) se dice que son disjuntos siempre que\(A \cap B = \emptyset\).

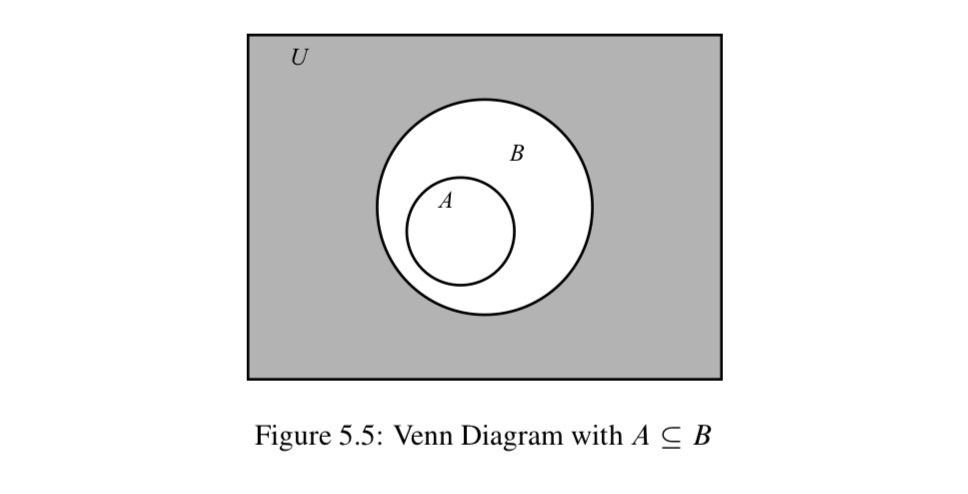
Por ejemplo, el diagrama de Venn en la Figura 5.5 muestra dos conjuntos\(A\) y\(B\) con\(A \subseteq B\). La región sombreada es la región que representa\(B^c\). Del diagrama de Venn, parece que\(A \cap B^c = \emptyset\). Esto significa que\(A\) y\(B^c\) son disjuntas. El ejemplo anterior sugiere que la siguiente proposición es cierta:

Si\(A \subseteq B\), entonces\(A \cap B^c = \emptyset\).

Si quisiéramos probar esta proposición, una “pregunta atrasada” razonable es, “¿Cómo demostramos que un conjunto (es decir\(A \cap B^c\)) es igual al conjunto vacío?”

Esta pregunta parece difícil de responder ya que ¿cómo demostramos que un conjunto está vacío? Esta es una instancia en la que probar lo contrapositivo o usar una prueba por contradicción podrían ser enfoques razonables. Para ilustrar estos métodos, supongamos que la proposición que estamos tratando de probar es de la siguiente forma:

Si\(P\), entonces\(T = \emptyset\).

Si optamos por probar lo contrapositivo o utilizar una prueba por contradicción, lo asumiremos\(T \ne \emptyset\). Estos métodos se pueden esbozar de la siguiente manera:

• El contrapositivo de “Si\(P\), entonces\(T = \emptyset\)” es, “Si\(T \ne \emptyset\), entonces”\(\urcorner P\). Entonces en este caso, asumiríamos\(T \ne \emptyset\) y trataríamos de probar\(\urcorner P\).
• Usando una prueba por contradicción, lo asumiríamos\(P\) y asumiríamos\(T \ne \emptyset\). A partir de estos dos supuestos, intentaríamos derivar una contradicción.

Una ventaja de estos métodos es que cuando asumimos eso\(T \ne \emptyset\), entonces sabemos que existe un elemento en el conjunto\(T\). Entonces podemos usar ese elemento en el resto de la prueba. Demostraremos una de las declaraciones condicionales para la Proposición 5.14 demostrando su contrapositiva. El comprobante de la otra declaración condicional asociada a la Proposición 5.14 es Ejercicio (10).

Proposición 5.14

Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Entonces\(A \subseteq B\) si y sólo si\(A \cap B^c = \emptyset\).

Prueba

Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Primero probaremos eso si\(A \subseteq B\), entonces\(A \cap B^c = \emptyset\), demostrando su contrapositivo. Es decir, vamos a probar

Si\(A \cap B^c \ne \emptyset\), entonces\(A \not\subseteq B\).

Entonces asumamos eso\(A \cap B^c \ne \emptyset\). Vamos a probar que\(A \not\subseteq B\) demostrando que debe existir un elemento\(x\) tal que\(x \in A\) y\(x \notin B\).

Ya que\(A \cap B^c \ne \emptyset\), existe un elemento\(x\) que está en\(A \cap B^c\). Esto significa que

\(x \in A\)y\(x \in B^c\).

Ahora el hecho de que eso\(x \in B^c\) significa eso\(x \notin B\). De ahí que podamos concluir que

\(x \in A\)y\(x \notin B\).

Esto quiere decir que\(A \not\subseteq B\), y de ahí, hemos demostrado que si\(A \cap B^c \ne \emptyset\), entonces\(A \not\subseteq B\), y por lo tanto, hemos demostrado que si\(A \subseteq B\), entonces\(A \cap B^c = \emptyset\).

La prueba de que si\(A \cap B^c = \emptyset\), entonces\(A \subseteq B\) es Ejercicio (10).

Comprobación de progreso 5.15: Demostrando que dos conjuntos son disarticulados

Se ha señalado que muchas veces es posible probar que dos conjuntos son disjuntos mediante el uso de una prueba por contradicción. En este caso, suponemos que los dos conjuntos no son disjuntos y por lo tanto, hay intersección no está vacía. Utilice este método para demostrar que los dos conjuntos siguientes son disjoint.

\(A = \{x \in \mathbb{Z}\ |\ x \equiv 3 \text{ (mod 12)}\}\)y\(B = \{y \in \mathbb{Z}\ |\ y \equiv 2 \text{ (mod 8)}\}\)

Contestar

Agrega textos aquí. No elimine primero este texto.

Un comentario final

Hemos utilizado el método de elegir un elemento para probar las Proposiciones 5.7, 5.11 y 5.14. Las pruebas que involucran conjuntos que usan este método a veces se refieren a pruebas de búsqueda de elementos. Este nombre se usa ya que el método básico es elegir un elemento arbitrario de un conjunto y “perseguirlo” hasta que demuestres que debe estar en otro conjunto.

Ejercicios para la Sección 5.2

1. Dejar\(A = \{x \in \mathbb{R}\ |\ x^2 < 4\}\) y dejar\(B = \{x \in \mathbb{R}\ |\ x < 2\}\)
   
   (a)\(A \subseteq B\) ¿Es? Justifica tu conclusión con una prueba o un contraejemplo.
   b) ¿Es\(B \subseteq A\)? Justifica tu conclusión con una prueba o un contraejemplo.
2. Dejar\(A\),\(B\), y\(C\) ser subconjuntos de un conjunto universal\(U\).
   
   (a) Dibujar un diagrama de Venn con\(A \subseteq B\) y\(B \subseteq C\). ¿Eso parece\(A \subseteq C\)?
   b) Demostrar la siguiente proposición:
   Si\(A \subseteq B\) y\(B \subseteq C\), entonces\(A \subseteq C\).
   Nota: Esto puede parecer un resultado obvio. Sin embargo, una de las razones de este ejercicio es proporcionar práctica para escribir correctamente una prueba de que un conjunto es un subconjunto de otro conjunto. Entonces debemos comenzar la prueba asumiendo que\(A \subseteq B\) y\(B \subseteq C\). Entonces deberíamos elegir un elemento arbitrario de\(A\).
3. Dejar\(A = \{x \in \mathbb{Z}\ |\ x \equiv 7 \text{ (mod 8)}\}\) y\(B = \{x \in \mathbb{Z}\ |\ x \equiv 3 \text{ (mod 4)}\}\).
   
   a) Enumerar al menos cinco elementos diferentes del conjunto\(A\) y al menos cinco elementos del conjunto\(B\).
   b) ¿Es\(A \subseteq B\)? Justifica tu conclusión con una prueba o un contraejemplo.
   c) ¿Es\(B \subseteq A\)? Justifica tu conclusión con una prueba o un contraejemplo.
4. Dejar\(C = \{x \in \mathbb{Z}\ |\ x \equiv 7 \text{ (mod 9)}\}\) y\(D = \{x \in \mathbb{Z}\ |\ x \equiv 1 \text{ (mod 3)}\}\).
   
   a) Enumerar al menos cinco elementos diferentes del conjunto\(C\) y al menos cinco elementos del conjunto\(D\).
   b) ¿Es\(C \subseteq D\)? Justifica tu conclusión con una prueba o un contraejemplo.
   c) ¿Es\(D \subseteq C\)? Justifica tu conclusión con una prueba o un contraejemplo.
5. En cada caso, determinar si\(A \subseteq B\)\(B \subseteq A\),\(A = B\),,\(A \cap B = \emptyset\) o ninguno de estos.
   
   a)\(A = \{x \in \mathbb{Z}\ |\ x \equiv 2 \text{ (mod 3)}\}\) y\(B = \{y \in \mathbb{Z}\ |\ 6 \text{ divides } (2y - 4)\}\).
   b)\(A = \{x \in \mathbb{Z}\ |\ x \equiv 3 \text{ (mod 4)}\}\) y\(B = \{y \in \mathbb{Z}\ |\ 3 \text{ divides } (y - 2)\}\).
   c)\(A = \{x \in \mathbb{Z}\ |\ x \equiv 1 \text{ (mod 5)}\}\) y\(B = \{x \in \mathbb{Z}\ |\ y \equiv 7 \text{ (mod 10)}\}\)
6. Para probar las siguientes igualdades establecidas, puede ser necesario utilizar algunas de las propiedades de números reales positivos y negativos. Por ejemplo, puede ser necesario utilizar los hechos que:

   \(\bullet\)El producto de dos números reales es positivo si y sólo si los dos números reales son ambos positivos o ambos son negativos.

   \(\bullet\)El producto de dos números reales es negativo si y sólo si uno de los dos números es positivo y el otro es negativo.
   
   Por ejemplo, si\(x (x - 2) < 0\), entonces podemos concluir que ya sea (1)\(x < 0\) y\(x - 2 > 0\) o (2)\(x > 0\) y\(x - 2 < 0\). No obstante, en el primer caso, debemos tener\(x < 0\) y\(x > 2\), y esto es imposible. Por lo tanto, concluimos que\(x > 0\) y\(x - 2 < 0\), lo que significa que\(0 < x < 2\).
   
   Utilice el método de elegir un elemento para probar cada uno de los siguientes:
   
   (a)\(\{x \in \mathbb{R}\ |\ x^2 - 3x - 10 < 0\} = \{x \in \mathbb{R}\ |\ -2 < x < 5\}\)
   (b)\(\{x \in \mathbb{R}\ |\ x^2 - 5x + 6 < 0\} = \{x \in \mathbb{R}\ |\ 2 < x < 3\}\)
   (c)\(\{x \in \mathbb{R}\ |\ x^2 \ge 4\} = \{x \in \mathbb{R}\ |\ x \le -2\} \ cup \{x \in \mathbb{R}\ |\ x \ge 2\}\)

7. Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\). Demostrar cada uno de los siguientes:
   
   a\(A \cap B \subseteq A\)
   )\(A \subseteq A \cup B\)
   b)\(A \cap A = A\)
   c) d\(A \cup A = A\)
   ) e\(A \cap \emptyset = \emptyset\)
   ) f)\(A \cup \emptyset = A\)
8. Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\). De la Proposición 5.10, sabemos que si\(A \subseteq B\), entonces\(B^c \subseteq A^c\). Ahora prueba la siguiente proposición:

   Para todos los conjuntos (A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\),\(A \subseteq B\) si y solo si\(B^c \subseteq A^c\).

9. ¿La siguiente proposición es verdadera o falsa? Justifica tu conclusión con una prueba o un contraejemplo.
   
   Para todos los conjuntos (A\) y\(B\) ser subconjuntos de algún conjunto universal\(U\), los conjuntos\(A \cap B\) y\(A - B\) son disjuntos.
10. Completa la prueba de la Proposición 5.14 probando la siguiente declaración condicional:
    
    Let (A\) y\(B\) ser subconjuntos de algún conjunto universal. Si\(A \cap B^c = \emptyset\), entonces\(A \subseteq B\).
11. Dejar\(A\),\(B\),\(C\), y\(D\) ser subconjuntos de algún conjunto universal\(U\). ¿Son verdaderas o falsas las siguientes proposiciones? Justifica tus conclusiones.
    
    (a) Si\(A \subseteq B\) y\(C \subseteq D\) y\(A\) y\(C\) son disjuntas, entonces\(B\) y\(D\) son disjuntas.
    b) Si\(A \subseteq B\) y y\(C \subseteq D\)\(B\) y\(D\) son disjuntas, entonces\(A\) y\(C\) son disjuntas.
12. Dejar\(A\),\(B\), y\(C\) ser subconjuntos de un conjunto universal\(U\). Demostrar: a
    
    ) Si\(A \subseteq B\), entonces\(A \cap C \subseteq B \cap C\).
    b) Si\(A \subseteq B\), entonces\(A \cup C \subseteq B \cup C\).
13. Dejar\(A\),\(B\), y\(C\) ser subconjuntos de un conjunto universal\(U\). ¿Son verdaderas o falsas las siguientes proposiciones? Justifica tus conclusiones.
    
    (a) Si\(A \cap C \subseteq B \cap C\), entonces\(A \subseteq B\).
    b) Si\(A \cup C \subseteq B \cup C\), entonces\(A \subseteq B\).
    (c) Si\(A \cup C = B \cup C\), entonces\(A = B\).
    d) Si\(A \cap C = B \cup C\), entonces\(A = B\).
    e) Si\(A \cup C = B \cup C\) y\(A \cap C = B \cap C\), entonces\(A = B\).
14. Demostrar la siguiente proposición:
    
    Para todos los conjuntos\(A\)\(B\),, y\(C\) que son subconjuntos de algún conjunto universal, si\(A \cap B = A \cap C\) y\(A^c \cap B = A^c \cap C\), entonces\(B = C\).
15. ¿Son verdaderas o falsas las siguientes declaraciones bicondicionales? Justifica tu conclusión. Si se determina que una declaración bicondicional es falsa, debe determinar claramente si una de las declaraciones condicionales dentro de ella es verdadera y proporcionar una prueba de esta declaración condicional.
    
    (a) Para todos los subconjuntos\(A\) y\(B\) de algún conjunto universal\(U\),\(A \subseteq B\) si y sólo si\(A \cap B^c = \emptyset\).
    b) Para todos los subconjuntos\(A\) y\(B\) de algún conjunto universal\(U\),\(A \subseteq B\) si y sólo si\(A \cup B = B\).
    c) Para todos los subconjuntos\(A\) y\(B\) de algún conjunto universal\(U\),\(A \subseteq B\) si y sólo si\(A \cap B = A\).
    d) Para todos los subconjuntos\(A\),\(B\), y\(C\) de algún conjunto universal\(U\),\(A \subseteq B \cup C\) si y sólo si\(A \subseteq B\) o\(A \subseteq C\).
    e) Para todos los subconjuntos\(A\),\(B\), y\(C\) de algún conjunto universal\(U\),\(A \subseteq B \cup C\) si y sólo si\(A \subseteq B\) y\(A \subseteq C\).
16. Dejar\(S\),\(T\),\(X\), y\(Y\) ser subconjuntos de algún conjunto universal. Supongamos que
    
    (i)\(S \cup T \subseteq X \cup Y\); (ii)\(S \cap T = \emptyset\); y (iii)\(X \subseteq S\).
    
    a) Utilizando el supuesto (i), ¿qué conclusión (es) puede (n) hacerse si se sabe que\(a \in T\)?
    b) Utilizando la suposición ii), ¿qué conclusión (es) puede (n) hacerse si se sabe que\(a \in T\)?
    c) Utilizando los tres supuestos, ya sea probarlo\(T \subseteq Y\) o explicar por qué no es posible hacerlo.
17. Evaluación de Pruebas
    Consulte las instrucciones para Ejercicio (19) en la página 100 de la Sección 3.1.

    (a)

    Dejar\(A\),\(B\), y\(C\) ser subconjuntos de algún conjunto universal. Si\(A \not\subseteq B\) y\(B \not\subseteq C\), entonces\(A \not\subseteq C\).

    Prueba

    Suponemos que\(A\),\(B\), y\(C\) ser subconjuntos de algún conjunto universal y eso\(A \not\subseteq B\) y\(B \not\subseteq C\). Esto quiere decir que existe un elemento\(x\) en el\(A\) que no está adentro\(B\) y existe un elemento\(x\) que está dentro\(B\) y no en\(C\). Por lo tanto\(x \notin C\),\(x \in A\) y, y eso lo hemos demostrado\(A \not\subseteq C\).

    b)

    Dejar\(A\),\(B\), y\(C\) ser subconjuntos de algún conjunto universal. Si\(A \cap B = A \cap C\), entonces\(B = C\).

    Prueba

    Eso lo asumimos\(A \cap B = A \cap C\) y lo demostramos\(B = C\). Primero lo demostraremos\(B \subseteq C\).

    Así que vamos\(x \in B\). Si\(x \in A\), entonces\(x \in A \cap B\), y por lo tanto,\(x \in A \cap C\). De esto podemos concluir que\(x \in C\). Si\(x \notin A\), entonces\(x \notin A \cap B\), y por lo tanto,\(x \notin A \cap C\). Sin embargo\(x \notin A\), ya que, podemos concluir que\(x \in C\). Por lo tanto,\(B \subseteq C\).

    La prueba que se\(C \subseteq B\) pueda hacer de manera similar. De ahí,\(B = C\).

    Dejar\(A\),\(B\), y\(C\) ser subconjuntos de algún conjunto universal. Si\(A \not\subseteq B\) y\(B \subseteq C\), entonces\(A \not\subseteq C\).

    Prueba

    Supongamos que\(A \not\subseteq B\) y\(B \subseteq C\). Ya que\(A \not\subseteq B\), existe un elemento\(x\) tal que\(x \in A\) y\(x \notin B\). Ya que\(B \subseteq C\), podemos concluir que\(x \notin C\). De ahí,\(x \in A\) y\(x \notin C\), y eso lo hemos demostrado\(A \not\subseteq C\).

Exploraciones y actividades

18. Uso del Método Choose-an-Element en una Configuración Diferente. Hemos utilizado el método de elegir un elemento para probar resultados sobre conjuntos. Este método, sin embargo, es una técnica de prueba general y se puede utilizar en entornos distintos a la teoría de conjuntos. A menudo se usa cada vez que nos encontramos con un cuantificador universal en una declaración en el proceso hacia atrás. Considera la siguiente proposición.

Proposición 5.16.

Dejar\(a\),\(b\) y\(t\) ser enteros con\(t \ne 0\). Si\(t\) divide\(a\) y\(t\) divide\(b\), entonces para todos los enteros\(x\) y\(y\),\(t\) divide\((ax + by)\).

(a) Siempre que nos encontremos con una nueva proposición, es buena idea explorar la proposición observando ejemplos específicos. Por ejemplo, vamos\(a = 20\),\(b = 12\), y\(t = 4\). En este caso,\(t\) |\(a\) y\(t\) |\(b\). En cada uno de los siguientes casos, determinar el valor de\((ax + by)\) y determinar si\(t\) divide\((ax + by)\).

i.\(x = 1\),\(y = 1\).
ii. \(x = 1\),\(y = -1\).
iii. \(x = 2\),\(y = 2\).
iv. \(x = 2\),\(y = -3\).
v\(y = 3\).\(x = -2\),.
vi. \(x = -2\),\(y = -5\).

(b) Repetir la Parte (18a) con\(a = 21\)\(b = 6\), y\(t = 3\).

Observe que la conclusión del enunciado condicional en esta proposición involucra al cuantificador universal. Entonces, en el proceso atrasado, habríamos

\(Q\): Para todos los enteros\(x\) y\(y\),\(t\) divide\(ax + by\).

Los “elementos” en esta oración son los enteros\(x\) y\(y\). En este caso, estos enteros no tienen “propiedad dada” que no sea que sean enteros. El “algo que pasa” es lo que\(t\) divide\((ax + by)\). Esto quiere decir que en el proceso hacia adelante, podemos utilizar la hipótesis de la proposición y elegir enteros\(x\) y\(y\). Es decir, en el proceso de avance, podríamos haber

\(P\):\(a\)\(b\),, y\(t\) son enteros con\(t \ne 0\),\(t\) divide\(a\) y\(t\) divide\(b\).

\(P\)1: Dejar\(x \in \mathbb{Z}\) y dejar\(y \in \mathbb{Z}\).

c) Cumplimentar la siguiente prueba de la Proposición 5.16.

Comprobante. Dejar\(a\),\(b\) y\(t\) ser enteros con\(t \ne 0\), y asumir que\(t\) divide\(a\) y\(t\) divide\(b\). Eso lo demostraremos para todos los enteros\(x\) y\(y\),\(t\) dibídes\((ax + by)\).

Así que vamos\(x \in \mathbb{Z}\) y vamos\(y \in \mathbb{Z}\). Desde\(t\) divide\(a\), existe un entero\(m\) tal que....

Contestar

Agrega textos aquí. No elimine primero este texto.