5.4: Productos cartesianos

PREVIAR ACTIVIDAD\(\PageIndex{1}\): An Equation with Two Variables

En la Sección 2.3, se introdujo el concepto del conjunto de verdad de una oración abierta con una variable. Esto se definió como el conjunto de todos los elementos del conjunto universal que pueden ser sustituidos por la variable para hacer de la oración abierta una declaración verdadera.

En cursos previos de matemáticas, también hemos tenido experiencia con oraciones abiertas con dos variables. Por ejemplo, si asumimos que x e y representan números reales, entonces la ecuación

\(2x + 3y = 12\)

es una oración abierta con dos variables. Un elemento del conjunto de verdad de esta oración abierta (también llamada solución de la ecuación) es un par ordenado (\(a\),\(b\)) de números reales de manera que cuando\(a\) se sustituye\(x\) y\(b\) se sustituye por\(y\), la oración abierta se convierte en una declaración verdadera (una verdadera ecuación en este caso). Por ejemplo, vemos que el par ordenado (6, 0) está en la verdad establecido para esta oración abierta ya que

\(2 \cdot 6 + 3 = 12\)

es una verdadera declaración. Por otro lado, el par ordenado (4, 1) no está en la verdad fijada para esta frase abierta ya que

\(2 \cdot 4 + 3 \cdot 1 = 12\)

es una declaración falsa.

Nota Importante: El orden de los dos números en el par ordenado es muy importante. Estamos usando la convención de que el primer número va a ser sustituido\(x\) y el segundo número es para ser sustituido\(y\). Con esta convención, (3, 2) es una solución de la ecuación\(2x + 3y = 12\), pero (2, 3) no es una solución de esta ecuación.

1. Enumere seis elementos diferentes del conjunto de verdad (a menudo llamado conjunto de soluciones) de la oración abierta con dos variables\(2x + 3y = 12\).
2. De cursos previos de matemáticas, sabemos que la gráfica de la ecuación\(2x + 3y = 12\) es una línea recta. Esboce la gráfica de la ecuación\(2x + 3y = 12\) en el plano\(xy\) -coordenada. ¿Qué muestra la gráfica de la ecuación\(2x + 3y = 12\)?
3. Escriba una descripción del conjunto de soluciones\(S\) de la ecuación\(2x + 3y = 12\) usando la notación del constructor de conjuntos.

PREVIAR ACTIVIDAD\(\PageIndex{1}\): The Cartesian Product of Two Sets

En Preview Activity\(\PageIndex{1}\), trabajamos con pares ordenados sin proporcionar una definición formal de un par ordenado. En cambio, confiamos en su trabajo anterior con pares ordenados, principalmente de graficar ecuaciones con dos variables. A continuación se presenta una definición formal de un par ordenado.

Definición: par ordenado

Dejar\(A\) y\(B\) ser conjuntos. Un par ordenado (con primer elemento de\(A\) y segundo elemento de\(B\)) es un solo par de objetos, denotado por (\(a\),\(b\)), con\(a \in A\) y\(b \in B\) y un orden implícito. Esto significa que para que dos pares ordenados sean iguales, deben contener exactamente los mismos objetos en el mismo orden. Es decir, si\(a, c \in A\) y\(b, d \in B\), entonces

(\(a\),\(b\)) = (\(c\),\(d\)) si y sólo si\(a = c\) y\(b = d\).

Los objetos en el par ordenado se llaman las coordenadas del par ordenado. En el par ordenado (\(a\),\(b\)),\(a\) es la primera coordenada y\(b\) es la segunda coordenada.

Ahora vamos a introducir una nueva operación de conjunto que da una forma de combinar elementos de dos conjuntos dados para formar pares ordenados. La idea básica es que crearemos un conjunto de pares ordenados.

Definición: producto cartesiano

Si\(A\) y\(B\) son conjuntos, entonces el producto cartesiano,\(A \times B\), de\(A\) y\(B\) es el conjunto de todos los pares ordenados (\(x\),\(y\)) donde\(x \in A\) y\(y \in B\). Usamos la notación\(A \times B\) para el producto cartesiano de\(A\) y\(B\), y usando la notación set builder, podemos escribir

\(A \times B = \{(x, y)\ |\ x \in A \text{ and } y \in B\}\).

Frecuentemente leemos\(A \times B\) como "\(A\)cruz”\(B\). En el caso en que los dos conjuntos sean iguales, escribiremos\(A^2\) para\(A \times A\). Es decir,

\(A^2 = A \times A = \{(a, b)\ |\ a \in A \text{ and } b \in A\}\).

Vamos\(A\ = \) {1, 2, 3} y\(B\ = \) {\(a\),\(b\)}.

1. ¿Está el par ordenado (3,\(a\)) en el producto cartesiano\(A \times B\)? Explique.
2. ¿Está el par ordenado (3,\(a\)) en el producto cartesiano\(A \times A\)? Explique.
3. ¿El par ordenado (3, 1) está en el producto cartesiano\(A \times A\)? Explique.
4. Usando el método roster para especificar todos los elementos de\(A \times B\). (Recuerda que los elementos de\(A \times B\) serán ordenados pares.
5. Utilice el método roster para especificar todos los elementos del conjunto\(A \times A = A^2\).
6. Para cualquier conjunto\(C\) y\(D\), explique cuidadosamente lo que significa decir que el par ordenado (\(x\),\(y\)) no está en el producto cartesiano\(C \times D\).

Productos Cartesianos

Al trabajar con productos cartesianos, es importante recordar que el producto cartesiano de dos juegos es en sí mismo un conjunto. Como conjunto, consiste en una colección de elementos. En este caso, los elementos de un producto cartesiano son pares ordenados. Deberíamos pensar en un par ordenado como un solo objeto que consiste en otros dos objetos en un orden especificado. Por ejemplo,

• Si\(a \ne 1\), entonces el par ordenado (1,\(a\)) no es igual al par ordenado (\(a\), 1). Es decir, (1,\(a\))\(\ne\) (\(a\), 1).
• Si\(A\ = \) {1, 2, 3} y\(B\ =\) {\(a\),\(b\)}, entonces el par ordenado (3,\(a\)) es un elemento del conjunto\(A \times B\). Es decir, (3,\(a\))\(\in A \times B\).
• Si\(A\ = \) {1, 2, 3} y\(B\ =\) {\(a\),\(b\)}, entonces el par ordenado (5,\(a\)) no es un elemento del conjunto\(A \times B\) desde\(5 \notin A\). Es decir,\((5, a) \notin A \times B\).

En la Sección 5.3, estudiamos ciertas propiedades de unión de conjuntos, intersección de conjuntos y complementos de conjuntos, que denominamos álgebra de conjuntos. Ahora comenzaremos algo similar para los productos cartesianos. Comenzamos por examinar algunos ejemplos específicos en la Comprobación de Progreso 5.23 y un poco más tarde en la Comprobación de Progreso 5.24.

comprobación de progreso 5.23 (relaciones entre productos cartesianos)

Vamos\(A =\) {1, 2, 3},\(T =\) {a, b}, y\(C =\) {a, c}. Entonces podemos formar nuevos conjuntos a partir de todas las operaciones de conjunto que hemos estudiado. Por ejemplo,\(B \cap C =\) {\(a\)}, y así

\(A \times (B \cap C) = \{(1, a), (2, a), (3, a)\}.\)

1. Utilice el método roster para enumerar todos los elementos (pares ordenados) en cada uno de los siguientes conjuntos:
   
   (a)\(A \times B\)
   (b)\(T \times B\)
   (c)\(A \times C\)
   (d)\(A \times (B \cap C)\)
   (e)\((A \times B) \cap (A \times C)\)
   (f)\(A \times (B \cup C)\)
   (g)\((A \times B) \cup (A \times C)\)
   (h)\(A \times (B - C)\)
   (i)\((A \times B) - (A \times C)\)
   (j)\(B \times A\)
2. Enumere todas las relaciones entre los conjuntos en la Parte (1) que observe.

Responder

Agrega textos aquí. No elimine primero este texto.

El Plano Cartesiano

En Preview Activity\(\PageIndex{1}\), esbozamos la gráfica de la ecuación\(2x + 3y = 12\) en el\(xy\) plano -plano. Este\(xy\) -plano, con el que estás familiarizado, es una representación del conjunto\(\mathbb{R} \times \mathbb{R}\) o\(\mathbb{R} ^2\). A este plano se le llama el plano cartesiano.

La idea básica es que cada par ordenado de números reales corresponde a un punto en el plano, y cada punto del plano corresponde a un par ordenado de números reales. Esta representación geométrica de\(\mathbb{R} ^2\) es una extensión de la representación geométrica de\(\mathbb{R}\) como una línea recta cuyos puntos corresponden a números reales.

Dado que el producto cartesiano\(\mathbb{R} ^2\) corresponde al plano cartesiano, el producto cartesiano de dos subconjuntos de\(\mathbb{R}\) corresponde a un subconjunto del plano cartesiano. Por ejemplo, si\(A\) es el intervalo [1, 3], y\(B\) es el intervalo [2, 5], entonces

\(A \times B = \{(x, y) \in \mathbb{R} ^2\ |\ 1 \le x \le 3 \text{ and } 2 \le y \le 5\}.\)

Entonces se\(A \times B\) puede dibujar una gráfica del conjunto en el plano cartesiano como se muestra en la Figura 5.6.

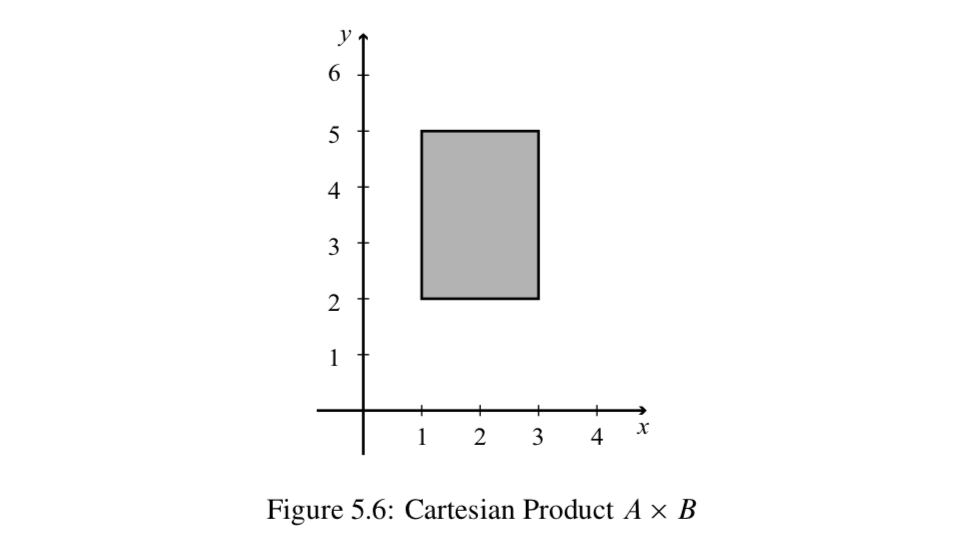
Esto ilustra que la gráfica de un producto cartesiano de dos intervalos de longitud finita en\(\mathbb{R}\) corresponde al interior de un rectángulo y posiblemente parte o la totalidad de su límite. La línea continua para el límite en la Figura 5.6 indica que el límite está incluido. En este caso, el producto cartesiano contenía todo el límite del rectángulo. Cuando la gráfica no contiene una porción del límite, usualmente dibujamos esa porción del límite con una línea punteada.

Nota: Una Precaución sobre la Notación. La notación estándar para un intervalo abierto en\(\mathbb{R}\) es la misma que la notación para un par ordenado, que es un elemento de\(\mathbb{R} \times \mathbb{R}\). Necesitamos usar el contexto en el que se usa la notación para determinar a qué interpretación se pretende. Por ejemplo,

• Si escribimos (\(sqrt 2\), 7)\(\in \mathbb{R} \times \mathbb{R}\), entonces estamos usando (\(sqrt 2\), 7) para representar un par ordenado de números reales.
• Si escribimos (1, 2)\(\times\) {4}, entonces estamos interpretando (1, 2) como un intervalo abierto. Podríamos escribir

(1, 2)\(\times\) {4} = {(\(x\), 4) | 1 <\(x\) < 2}.

La siguiente comprobación de progreso explora algunas de las mismas ideas exploradas en la Comprobación de progreso 5.23, excepto que se utilizan intervalos de números reales para los conjuntos.

Comprobación de Progreso 5.24: Productos Cartesianos de Intervalos

Usaremos los siguientes intervalos que son subconjuntos de\(\mathbb{R}\).

\(A =\)[0, 2]\(T =\) (1, 2)\(B =\) [2, 4)\(C =\) (3, 5]

1. Dibuja una gráfica de cada uno de los siguientes subconjuntos del plano cartesiano y escribe cada subconjunto usando la notación del constructor de conjuntos.
   
   (a)\(A \times B\)
   (b)\(T \times B\)
   (c)\(A \times C\)
   (d)\(A \times (B \cap C)\)
   (e)\((A \times B) \cap (A \times C)\)
   (f)\(A \times (B \cup C)\)
   (g)\((A \times B) \cup (A \times C)\)
   (h)\(A \times (B - C)\)
   (i)\((A \times B) - (A \times C)\)
   (j)\(B \times A\)
2. Enumere todas las relaciones entre los conjuntos en la Parte (1) que observe.

Responder

Agrega textos aquí. No elimine primero este texto.

Uno de los propósitos del trabajo en Progress Checks 5.23 y 5.24 fue indicar la plausibilidad de muchos de los resultados contenidos en el siguiente teorema.

Teorema 5.25

Dejar\(A\),\(B\). y\(C\) ser conjuntos. Entonces

1. \(A \times (B \cap C) = (A \times B) \cap (A \times C)\)
2. \(A \times (B \cup C) = (A \times B) \cup (A \times C)\)
3. \((A \cap B) \times C = (A \times C) \cap (B \times C)\)
4. \((A \cup B) \times C = (A \times C) \cup (B \times C)\)
5. \(A \times (B - C) = (A \times B) - (A \times C)\)
6. \((A - B) \times C = (A \times C) - (B \times C)\)
7. Si\(T \subseteq A\), entonces\(T \times B \subseteq A \times B\).
8. Si\(T \subseteq B\), entonces\(A \times Y \subseteq A \times B\).

No vamos a probar todos estos resultados; más bien, probaremos la Parte (2) del Teorema 5.25 y dejaremos parte del resto a los ejercicios. Al construir estas pruebas, debemos tener en cuenta que los productos cartesianos son conjuntos, por lo que seguimos muchos de los mismos principios para probar las relaciones establecidas que se introdujeron en las Secciones 5.2 y 5.3.

La otra cosa a recordar es que los elementos de un producto cartesiano son pares ordenados. Entonces cuando iniciamos una prueba de un resultado como la Parte (2) del Teorema 5.25, el objetivo principal es demostrar que los dos conjuntos son iguales. Esto lo haremos demostrando que cada uno es un subconjunto del otro. Entonces, si queremos probarlo\(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\), podemos comenzar eligiendo un elemento arbitrario de\(A \times (B \cup C)\). El objetivo es entonces demostrar que este elemento debe estar en\((A \times B) \cup (A \times C)\). Cuando empezamos por elegir un elemento arbitrario de\(A \times (B \cup C)\), podríamos darle un nombre a ese elemento. Por ejemplo, podríamos empezar por dejar

\[u \text{ be an element of } A \times (B \cup C).\]

Entonces podemos usar la definición de “par ordenado” para concluir que

\[\text{there exists } x \in A \text{ and there exits } y \in B \cup C \text{ such that } u = (x, y).\]

Para probarlo\(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\), ahora debemos demostrar que el par ordenado\(u\) de (5.4.1) está adentro\(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\). Para ello, podemos usar la definición de unión de conjunto y demostrar que

\[u \in (A \times B) \text{ or } u \in (A \times C).\]

Ya que\(u = (x, y)\), podemos probar (5.4.3) demostrando que

\[(x \in A \text{ and } y \in B) \text{ or } (x \in A \text{ and } y \in C).\]

Si miramos las frases en (5.4.2) y (5.4.4), parecería que estamos muy cerca de demostrarlo\(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\). A continuación se presenta una prueba de la Parte (2) del Teorema 5.25.

Teorema 5.25 (Parte (2)).

Dejar\(A\),\(B\). y\(C\) ser conjuntos. Entonces

\(A \times (B \cup C) = (A \times B) \cup (A \times C)\)

Prueba

Dejar\(A\),\(B\). y\(C\) ser conjuntos. Demostraremos que\(A \times (B \cup C)\) es igual a\((A \times B) \cup (A \times C)\) demostrando que cada conjunto es un subconjunto del otro conjunto.

Para probarlo\(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\), dejamos\(u \in A \times (B \cup C)\). Entonces existe\(x \in A\) y existe\(y \in B \cup C\) tal que\(u = (x, y)\). Ya que\(y \in B \cup C\), sabemos que\(y \in B\) o\(y \in C\).

En el caso donde\(y \in B\), tenemos\(u = (x, y)\), donde\(x \in A\) y\(y \in B\). Entonces en este caso,\(u \in A \times B\), y por lo tanto\(u \in (A \times B) \cup (A \times C)\). De igual manera, en el caso donde\(y \in C\), tenemos\(u = (x, y)\), donde\(x \in A\) y\(y \in C\). Entonces en este caso,\(u \in A \times C\) y, de ahí,\(u \in (A \times B) \cup (A \times C)\).

En ambos casos,\(u \in (A \times B) \cup (A \times C)\). De ahí que podamos concluir que si\(u\) es un elemento de\(A \times (B \cup C)\), entonces\(u \in (A \times B) \cup (A \times C)\), y esto demuestra que

\[A \times (B \cup C) \subseteq (A \times B) \cup (A \times C).\]

Ahora debemos probarlo\((A \times B) \cup (A \times C) \subseteq A \times (B \cup C)\). Entonces dejamos\(v \in (A \times B) \cup (A \times C)\). Entonces\(v \in (A \times B)\) o\(v \in (A \times C)\).

En el caso donde\(v \in (A \times B)\), sabemos que existe\(s \in A\) y existe\(t \in B\) tal que\(v = (s, t)\). Pero porque\(t \in C\), podemos concluir eso\(t \in B \cup C\) y, de ahí,\(v \in A \times (B \cup C)\).

En ambos casos,\(v \in A \times (B \cup C)\). De ahí que podamos concluir que si\(v \in (A \times B) \cup (A \times C)\), entonces\(v \in A \times (B \cup C)\), y esto demuestra que

\[(A \times B) \cup (A \times C) \subseteq A \times (B \cup C).\]

Las relaciones en (5.4.5) y (5.4.6) lo demuestran\(A \times (B \cup C) = (A \times B) \cup (A \times C)\).

Nota Final.

La definición de un par ordenado en Preview Activity\(\PageIndex{2}\) puede haber parecido una definición larga, pero en algunas áreas de las matemáticas, se necesita una definición aún más formal y precisa de “par ordenado”. Esta definición se explora en Ejercicio (10).

Ejercicios para la Sección 5.4

1. Vamos\(A =\) {1, 2},\(B =\) {\(a\),\(b\),\(c\),\(d\)}, y\(C =\) {1,\(a\),\(b\)}. Utilice el método roster para enumerar todos los elementos de cada uno de los siguientes conjuntos:
   
   (a)\(A \times B\)
   (b)\(B \times A\)
   (c)\(A \times C\)
   (d)\(A^2\)
   (e)\(A \times (B \cap C)\)
   (f) \((A \times B) \cap (A \times C)\)
   g\(A \times \emptyset\)
   ) h\(B \times \{2\}\)
2. Dibuje una gráfica de cada uno de los siguientes productos cartesianos en el plano cartesiano.
   
   a) [0, 2]\(\times\) [1, 3] b)
   (0, 2)\(\times\) (1, 3]
   c) [2, 3]\(\times\) {1}
   d) {1}\(\times\) [2, 3] e)
   (2, 4) f)\(\mathbb{R}\)\(\times\)
   (2, 4) (2, 4)\(\times\) \(\mathbb{R}\)
   (g)\(\mathbb{R}\)\(\times\) {-1}
   (h) {-1}\(\times\) [1, +\(\infty\))
3. Demostrar Teorema 5.25, Parte (1):\(A \times (B \cap C) = (A \times B) \cap (A \times C)\).
4. Demostrar Teorema 5.25, Parte (4):\((A \cup B) \times C = (A \times C) \cup (B \times C)\).
5. Demostrar Teorema 5.25, Parte (5):\(A \times (B - C) = (A \times B) - (A \times C)\).
6. Demostrar Teorema 5.25, Parte (7): Si\(T \subseteq A\), entonces\(T \times B \subseteq A \times B\).
7. Vamos\(A =\) {1},\(B =\) {2}, y\(C =\) {3}.
   
   a) Explique por qué\(A \times B \ne B \times A\).
   b) Explique por qué\(A \times B) \times C \ne A \times (B \times C)\).
8. Dejar\(A\) y\(B\) ser conjuntos no vacíos. Demostrar que\(A \times B = B \times A\) si y sólo si\(A = B\).
9. ¿La siguiente proposición es verdadera o falsa? Justifica tu conclusión.
   
   Dejar\(A\),\(B\) y\(C\) ser conjuntos con\(A \ne \emptyset\). Si\(A \times B = A \times C\), entonces\(B = C\). Explique dónde se necesita la suposición que\(A \ne \emptyset\) se necesita.
   
   Exploraciones y actividades
10. (Una definición teórica de conjuntos de un par ordenado) En matemáticas elementales, bastará con la noción de par ordenado introducida al inicio de esta sección. No obstante, si nos interesa un desarrollo formal del producto cartesiano de dos conjuntos, necesitamos una definición más precisa de par ordenado. A continuación se presenta una forma de hacer esto en cuanto a conjuntos. Esta definición se le atribuye a Kazimierz Kuratowski (1896 — 1980). Kuratowski fue un famoso matemático polaco cuyo trabajo principal fue en las áreas de topología y teoría de conjuntos. Fue nombrado Director de la Academia Polaca de Ciencias y se desempeñó en ese cargo por 19 años.
    
    Dejar\(x\) ser un elemento del conjunto\(A\), y dejar\(y\) ser un elemento del conjunto\(B\). El par ordenado (\(x\),\(y\)) se define como el conjunto\(\{\{x\}, \{x, y\}\}\). Es decir,
    \[(x, y) = \{\{x\}, \{x, y\}\}.\]
    (a) Explicar cómo esta definición nos permite distinguir entre los pares ordenados (3, 5) y (5, 3).
    
    b) Dejar\(A\) y\(B\) ser conjuntos y dejar\(a, c \in A\) y\(b, d \in B\). Utilice esta definición de par ordenado y el concepto de igualdad de conjunto para demostrar que\((a, b) = (c, d)\) si y sólo si\(a = c\) y\(b = d\).
    
    Un triple ordenado puede pensarse como un solo triple de objetos, denotado por (\(a\),\(b\),\(c\)), con un orden implícito. Esto significa que para que dos triples ordenados sean iguales, deben contener exactamente los mismos objetos en el mismo orden. Eso es\((a, b, c) = (p, q, r)\) si y sólo si\(a = p\),\(b = q\) y\(c = r\).
    
    (c) Dejar\(A\),\(B\) y\(C\) ser conjuntos, y dejar\(x \in A\),\(y \in B\), y\(z \in C\). Escribir una definición teórica de conjunto del triple ordenado\((x, y, z)\) similar a la definición teórica de conjunto de “par ordenado”.

Responder

Agrega textos aquí. No elimine primero este texto.