5.5: Familias de conjuntos indexados
- Page ID
- 116090
En la Sección 5.3, discutimos varias propiedades de las operaciones de conjunto. Ahora nos centraremos en las propiedades asociativas para la unión de conjuntos y la intersección de conjuntos. Observe que la definición de “conjunto de unión” nos dice cómo formar la unión de dos conjuntos. Es la ley asociativa la que nos permite discutir la unión de tres conjuntos. Usando la ley asociada, si\(A\)\(B\),, y\(C\) son subconjuntos de algún conjunto universal, entonces podemos\(A \cup B \cup C\) definir ser\((A \cup B) \cup C\) o\(A \cup ( B \cup C)\). Es decir,
\(A \cup B \cup C = (A \cup B) \cup C = A \cup (B \cup C).\)
Para esta actividad, el conjunto universal es N y utilizaremos los siguientes cuatro conjuntos:
\(A =\){1, 2, 3, 4, 5}
\(B =\){2, 3, 4, 5, 6}
\(C =\){3, 4, 5, 6, 7}
\(D =\){4, 5, 6, 7, 8}
- Utilice el método roster para especificar los conjuntos\(A \cup B \cup C\),\(B \cup C \cup D\),\(A \cap B \cap C\), y\(B \cap C \cap D\).
- Utilice el método roster para especificar cada uno de los siguientes conjuntos. En cada caso, asegúrese de seguir el orden especificado por los paréntesis.
(a)\((A \cup B \cup C) \cup D\)
(b)\(A \cup (B \cup C \cup D)\)
(c)\(A \cup (B \cup C) \cup D\)
(d)\((A \cup B) \cup (C \cup D)\)
(e)\((A \cap B \cap C) \cap D\)
(f)\(A \cap (B \cap C \cap D)\)
(g)\(A \cap (B \cap C) \cap D\)
(h)\((A \cap B) \cap (C \cap D)\) - Con base en el trabajo de la Parte (2), ¿importa la colocación de los paréntesis a la hora de determinar la unión (o intersección) de estos cuatro conjuntos? ¿Esto hace posible definir\(A \cup B \cup C \cup D\) y\(A \cap B \cap C \cap D\)?
Ya hemos visto que los elementos de un conjunto pueden ser ellos mismos conjuntos. Por ejemplo, el conjunto de potencia de un conjunto\(T\),\(\mathcal{P}(T)\), es el conjunto de todos los subconjuntos de\(T\). La frase, “un conjunto de conjuntos” suena confusa, por lo que a menudo usamos los términos colección y familia cuando queremos enfatizar que los elementos de un conjunto dado son ellos mismos conjuntos. Entonces diríamos que el conjunto de poder de\(T\) es la familia (o colección) de conjuntos que son subconjuntos de\(T\).
Uno de los propósitos del trabajo que hemos realizado hasta el momento en esta actividad previa fue mostrar que es posible definir la unión e intersección de una familia de conjuntos.
\(\mathcal{C}\)Déjese ser una familia de conjuntos. La unión sobre\(\mathcal{C}\) se define como el conjunto de todos los elementos que se encuentran en al menos uno de los conjuntos en\(\mathcal{C}\). Escribimos
\(\bigcup_{X \in \mathcal{C}}^{} X = \{x \in U\ |\ x \in X \text{ for some } X \in \mathcal{C}\}\)
La intersección sobre\(\mathcal{C}\) se define como el conjunto de todos los elementos que se encuentran en todos los conjuntos en\(\mathcal{C}\). Es decir,
\(\bigcap_{X \in \mathcal{C}}^{} X = \{x \in U\ |\ x \in X \text{ for some } X \in \mathcal{C}\}\)
Por ejemplo, considere los cuatro conjuntos\(A\),,\(B\)\(C\), y\(D\) utilizados anteriormente en esta actividad de vista previa y los conjuntos
\(S =\){5, 6, 7, 8, 9} y\(T =\) {6, 7, 8, 9, 10}
Luego podemos considerar las siguientes familias de conjuntos:\(\mathcal{A} = \{A, B, C, D\}\) y\(\mathcal{B} = \{A, B, C, D, S, T\}\)
- Explicar por qué
\(\bigcup_{X \in \mathcal{A}}^{} X = A \cup B \cup C \cup D\)y\(\bigcap_{X \in \mathcal{A}}^{} X = A \cap B \cap C \cap D\)
y utilice su trabajo en (1), (2), y (3) para determinar\(\bigcup_{X \in \mathcal{A}}^{} X\) y\(\bigcap_{X \in \mathcal{A}}^{} X\).
- Utilice el método de lista para especificar\(\bigcup_{X \in \mathcal{B}}^{} X\) y\(\bigcap_{X \in \mathcal{B}}^{} X\)
6. Utilice el método roster para especificar los conjuntos\((\bigcup_{X \in \mathcal{A}}^{} X)^c\) y\(\bigcap_{X \in \mathcal{A}}^{} X^c\). Recuerda que el conjunto universal es\(\mathbb{N}\).
A menudo usamos subíndices para identificar conjuntos. Por ejemplo, en Preview Activity\(\PageIndex{1}\), en lugar de usar\(A\)\(B\)\(C\),,, y\(D\) como los nombres de los conjuntos, podríamos haber usado\(A_1\),\(A_2\),\(A_3\), y\(A_4\). Cuando hacemos esto, estamos usando el subíndice como una etiqueta identificadora, o índice, para cada conjunto. También podemos usar esta idea para especificar una familia infinita de conjuntos. Por ejemplo, para cada número natural\(n\), definimos
\(C_n = \{n, n + 1, n + 2, n + 3, n + 4\}.\)
Entonces, si tenemos una familia de conjuntos\(\mathcal{C} = \{C_1, C_2, C_3, C_4\}\), usamos la notación\(\bigcup_{j = 1}^{4} C_j\) para significar lo mismo que\(\bigcup_{x \in \mathcal{C}}^{} X\).
- Determinar\(\bigcup_{j = 1}^{4} C_j\) y\(\bigcap_{j = 1}^{4} C_j\)
Podemos ver que con el uso de subíndices, ni siquiera tenemos que definir la familia de conjuntos\(\mathcal{A}\). Podemos trabajar con la familia infinita de conjuntos
\[\mathcal{C} ^{\ast} = \{A_n\ |\ n \in \mathbb{N}\}\]
y usar los subíndices para indicar qué conjuntos usar en una unión o una intersección. - Utilice el método roster para especificar cada uno de los siguientes pares de conjuntos. El conjunto universal es\(\mathbb{N}\).
(a)\(\bigcup_{j = 1}^{6} C_j\) y\(\bigcap_{j = 1}^{6} C_j\)
(b)\(\bigcup_{j = 1}^{8} C_j\) y\(\bigcap_{j = 1}^{8} C_j\)
(c)\(\bigcup_{j = 4}^{8} C_j\) y\(\bigcap_{j = 4}^{8} C_j\)
(d)\((\bigcap_{j = 1}^{4} C_j)^c\) y\(\bigcup_{j = 1}^{4} C_j ^c\)
La unión y la intersección sobre una familia de conjuntos indexados
Uno de los propósitos de las actividades de previsualización fue mostrar que a menudo nos encontramos con situaciones en las que están involucrados más de dos conjuntos, y es posible definir la unión e intersección de más de dos conjuntos. En Preview Activity\(\PageIndex{2}\), también vimos que a menudo es conveniente “indexar” los conjuntos en una familia de conjuntos. En particular, si\(n\) es un número natural y\(\mathcal{A} = \{A_1, A_2, ..., A_n\}\) es una familia de\(n\) conjuntos, entonces la unión de estos\(n\) conjuntos, denotada por\(A_1 \cup A_2 \cup \cdot\cdot\cdot \cup A_n\) o\(\bigcup_{j = 1}^{n} A_j\), se define como
\[\bigcup_{j = 1}^{n} A_j = \{x \in U\ |\ x \in A_j, \text{ for some } j \text{ with } 1 \le j \le n\}.\]
También podemos definir la intersección de estos\(n\) conjuntos, denotada por\(A_1 \cap A_2 \cap \cdot\cdot\cdot \cap A_n\) o\(\bigcap_{j = 1}^{n} A_j\), como
\[\bigcap_{j = 1}^{n} A_j = \{x \in U\ |\ x \in A_j, \text{ for some } j \text{ with } 1 \le j \le n\}.\]
También podemos ampliar esta idea para definir la unión e intersección de una familia que consta de infinitamente muchos conjuntos. Así que si\(\mathcal{B} = \{B_1, B_2, ..., B_n, ...\}\), entonces
\(\bigcup_{j = 1}^{\infty} B_j = \{x \in U\ |\ x \in B_j, \text{ for some } j \text{ with } j \ge 1\}\), y
\(\bigcap_{j = 1}^{\infty} B_j = \{x \in U\ |\ x \in B_j, \text{ for all } j \text{ with } j \ge 1\}\).
Por cada número natural\(n\), vamos\(A_n = \{1, n, n^2\}\). Por ejemplo,
\(A_1 = \{1\}\),\(A_2 = \{1, 2, 4\}\),\(A_3 = \{1, 3, 9\}\),
y
\(\bigcup_{j = 1}^{3} A_j = \{1, 2, 3, 4, 9\}\),\(\bigcap_{j = 1}^{3} A_j = \{1\}\).
Determine cada uno de los siguientes conjuntos:
- \(\bigcup_{j = 1}^{6} A_j\)
- \(\bigcap_{j = 1}^{6} A_j\)
- \(\bigcup_{j = 3}^{6} A_j\)
- \(\bigcap_{j = 3}^{6} A_j\)
- \(\bigcup_{j = 1}^{\infty} A_j\)
- \(\bigcap_{j = 1}^{\infty} A_j\)
- Contestar
-
Agrega textos aquí. No borre primero este texto.
En todos los ejemplos que hemos estudiado hasta ahora, hemos utilizado\(\mathbb{N}\) o un subconjunto de\(\mathbb{N}\) para indexar o etiquetar los conjuntos en una familia de conjuntos. Podemos usar otros conjuntos para indexar o etiquetar conjuntos en una familia de conjuntos. Por ejemplo, para cada número real\(x\), podemos\(B_x\) definir como el intervalo cerrado [x, x + 2]. Es decir,
\(B_x = \{y \in \mathbb{R}\ |\ x \le y \le x + 2\}\).
Por lo que hacemos la siguiente definición. En esta definición,\(\wedge\) es la letra griega mayúscula lambda y\(\alpha\) es la letra griega minúscula alfa.
Dejar\(\Lambda\) ser un conjunto no vacío y supongamos que para cada uno\(\alpha \in \wedge\), hay un conjunto correspondiente\(A_{\alpha}\). La familia de conjuntos\(\{A_{\alpha}\ |\ \alpha \in \wedge\}\) se denomina familia indexada de conjuntos indexados por\(\wedge\). Cada uno\(\alpha \in \wedge\) se llama índice y\(\Lambda\) se llama conjunto de indexación.
En cada una de las familias indexadas de conjuntos que hemos visto hasta ahora, si los índices eran diferentes, entonces los conjuntos eran diferentes. Es decir, si\(\Lambda\) es una indexación para la familia de conjuntos\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \wedge\}\), entonces si\(\alpha, \beta \in \wedge\) y\(\alpha \ne \beta\), entonces\(A_{\alpha} \ne A_{\beta}\). (Nota: La letra\(\beta\) es la beta minúscula griega.)
- Dejar\(\Lambda = \{1, 2, 3, 4\}\), y para cada uno\(n \in \Lambda\), dejar\(A_n = \{2n + 6, 16 - 3n\}\), y dejar\(\mathcal{A} = \{A_1, A_2, A_3, A_4\}\). Determinar\(A_1\),\(A_2\),\(A_3\), y\(A_4\).
- ¿La siguiente afirmación es verdadera o falsa para la familia indexada\(\mathcal{A}\) en (1)?
- Ahora vamos\(\Lambda = \mathbb{R}\). Para cada uno\(x \in \mathbb{R}\), defina\(B_x = \{0, x^2, x^4\}\). ¿Es cierta la siguiente afirmación para la familia indexada de conjunto\(\mathcal{B} = \{B_x\ |\ x \in \mathbb{R}\}\)?
Para todos\(x, y \in \mathbb{R}\), si\(x \ne y\), entonces\(B_x \ne B_y\).
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ahora replanteamos las definiciones de unión e intersección de una familia de conjuntos para una familia de conjuntos indexados.
Dejar\(\Lambda\) ser un conjunto de indexación no vacío y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia de conjuntos indexados. La unión sobre\(\mathcal{A}\) se define como el conjunto de todos los elementos que se encuentran en al menos uno de los conjuntos\(A_{\alpha}\), donde\(\alpha \in \wedge\). Escribimos
\(\bigcup_{\alpha \in \Lambda}^{} A_{\alpha} = \{x \in U\ |\ \text{ there exits an } \alpha \in \Lambda \text{ with } x \in A_{\alpha}\}\).
La intersección sobre (\ mathcal {A}\) es el conjunto de todos los elementos que están en todos los conjuntos\(A_{\alpha}\) para cada uno\(\alpha \in \Lambda\). Es decir,
\(\bigcap_{\alpha \in \wedge}^{} A_{\alpha} = \{x \in U\ |\ \text{ for all } \alpha \in \wedge, x \in A_{\alpha}\}\).
Para cada numbe real positivo\(\alpha\), deja\(A_{\alpha}\) ser el intervalo (-1,\(\alpha\)]. Es decir,
\(A_{\alpha} = \{x \in \mathbb{R}\ |\ -1 < x \le \alpha\}.\)
Si dejamos\(\mathbb{R} ^{+}\) ser el conjunto de números reales positivos, entonces tenemos una familia de conjuntos indexados por\(\mathbb{R} ^{+}\). Primero determinaremos la unión de esta familia de conjuntos. Observe que para cada uno\(\alpha \in mathbb{R} ^{+}\)\(\alpha \in A_{\alpha}\),, y si\(y\) es un número real con\(-1 < y \le 0\), entonces\(y \in A_{\alpha}\). También fíjese que si\(y \in \mathbb{R}\) y\(y < -1\), entonces para cada uno\(\alpha \in mathbb{R} ^{+}\),\(y \notin A_{\alpha}\). Con estas observaciones, concluimos que
\(\bigcup_{\alpha \in \mathbb{R} ^{+}}^{} A_{\alpha} = (-1, \infty) = \{x \in \mathbb{R}\ |\ -1 < x\}.\)
Para determinar la intersección de esta familia, observe que
- si\(y \in \mathbb{R}\) y\(y < -1\), entonces para cada uno\(\alpha \in \mathbb{R} ^{+}\),\(y \notin A_{\alpha}\);
- si\(y \in \mathbb{R}\) y\(-1 < y \le 0\), entonces\(y \in A_{\alpha}\) para cada uno\(\alpha \in mathbb{R} ^{+}\); y
- si\(y \in \mathbb{R}\) y\(y > 0\), entonces de dejamos\(\beta = \dfrac{y}{2}\),\(y > \beta\) y\(y \notin A_{\beta}\).
A partir de estas observaciones, concluimos que
\(\bigcap_{\alpha \in \mathbb{R} ^{+}}^{} A_{\alpha} = (-1, 0] = \{x \in \mathbb{R}\ |\ -1 < x \le 0\}.\)
Usando la familia de conjuntos del Ejemplo 5.28, para cada uno\(\alpha \in mathbb{R} ^{+}\), vemos que
\(A_{\alpha} ^c = (-\infty, 1] \cup (\alpha, \infty).\)
Utilice los resultados del Ejemplo 5.28 para ayudar a determinar cada uno de los siguientes conjuntos. Para cada conjunto, use notación de intervalo o notación de generador de conjuntos.
- \((\bigcup_{\alpha \in \mathbb{R} ^{+}}^{} A_{\alpha})^c\)
- \((\bigcap_{\alpha \in \mathbb{R} ^{+}}^{} A_{\alpha})^c\)
- \(\bigcap_{\alpha \in \mathbb{R} ^{+}}^{} A_{\alpha} ^c\)
- \(\bigcup_{\alpha \in \mathbb{R} ^{+}}^{} A_{\alpha} ^c\)
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Propiedades de Unión e Intersección
En Teorema 5.30, probaremos algunas propiedades de operaciones de conjuntos para familias indexadas de conjuntos. Algunas de estas propiedades son extensiones directas de propiedades correspondientes para dos conjuntos. Por ejemplo, ya hemos probado las Leyes de De Morgan para dos conjuntos en Teorema 5.20. El trabajo en las actividades de vista previa y Progress Check 5.29 sugiere que deberíamos obtener resultados similares usando operaciones de conjunto con una familia de conjuntos indexados. Por ejemplo, en Preview Activity\(\PageIndex{2}\), vimos que
\((\bigcap_{j = 1}^{4} A_j)^c = \bigcup_{j = 1}^{4} A_j ^c.\)
Dejar\(\Lambda\) ser un conjunto de indexación no vacío y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \wedge\}\) ser una familia de conjuntos indexados. Entonces
- Para cada uno\(\beta \in \Lambda\),\(\bigcap_{\alpha \in \Lambda} A_{\alpha} \subseteq A_{\beta}\)
- Para cada uno\(\beta \in \Lambda\),\(A_{\beta} \subseteq \bigcup_{\alpha \in \Lambda} A_{\alpha}\)
- \((\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})^c = \bigcup_{\alpha \in \Lambda}^{} A_{\alpha} ^c\)
- \((\bigcup_{\alpha \in \Lambda}^{} A_{\alpha})^c = \bigcap_{\alpha \in \Lambda}^{} A_{\alpha} ^c\)
Las partes (3) y (4) se conocen como Leyes de De Morgan.
- Prueba
-
Demostraremos Partes (1) y (3). Las pruebas de las Partes (2) y (4) están incluidas en el Ejercicio (4). Entonces dejamos\(\Lambda\) ser un conjunto de indexación no vacío y dejamos\(mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia indexada de conjuntos. Para probar la Parte (1), dejamos\(\beta \in \Lambda\) y notamos que si\(x \in \bigcap_{\alpha \in \Lambda}^{} A_{\alpha}\), entonces\(x \in A_{\alpha}\), para todos\(\alpha \in \Lambda\). Ya que\(\beta\) es un elemento en\(\Lambda\), podemos concluir que\(x \in A_{\beta}\). Esto lo demuestra\(\bigcap_{\alpha \in \Lambda}^{} A_{\alpha} \subseteq A_{\beta}\).
Para probar la Parte (3), probaremos que cada conjunto es un subconjunto del otro conjunto. Primero dejamos\(x \in (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})^c\). Esto significa que\(x \notin (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})\), y esto significa que
existe\(\beta \in \Lambda\) tal que\(x \notin A_{\beta}\).
De ahí,\(x \in A_{\beta} ^c\), lo que implica que\(x \in \bigcup_{\alpha \in \Lambda}^{} A_{\alpha} ^c\). Por lo tanto, hemos demostrado que
\[(\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})^c \subseteq \bigcup_{\alpha \in \Lambda}^{} A_{\alpha} ^c.\]
Ahora vamos\(y \in \bigcup_{\alpha \in \Lambda}^{} A_{\alpha} ^c\). Esto quiere decir que existe\(\beta \in \Lambda\) tal que\(y \in A_{\beta} ^c\) o\(y \notin A_{\beta}\). No obstante, ya que\(y \notin A_{\beta}\), podemos concluir que\(y \notin \bigcap_{\alpha \in \Lambda}^{} A_{\alpha}\) y, de ahí,\(y \in (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})^c\). Esto demuestra que
\[\bigcup_{\alpha \in \Lambda}^{} A_{\alpha} ^c \subseteq (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})^c.\]
Utilizando los resultados de (5.5.4) y (5.5.5), hemos demostrado que\((\bigcap_{\alpha \in \Lambda}^{} A_{\alpha})^c = \bigcup_{\alpha \in \Lambda}^{} A_{\alpha} ^c.\)
Muchas de las otras propiedades de las operaciones de conjunto también son verdaderas para familias indexadas de conjuntos. El teorema 5.31 establece las leyes distributivas para las operaciones de conjunto.
Dejar\(\Lambda\) ser un conjunto de indexación no vacío y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia indexada de conjuntos, y dejar\(B\) ser un conjunto. Entonces
- \(B \cap (\bigcup_{\alpha \in \Lambda}^{} A_{\alpha}) = \bigcup_{\alpha \in \Lambda}^{} (B \cap A_{\alpha})\), y
- \(B \cup (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha}) = \bigcap_{\alpha \in \Lambda}^{} (B \cup A_{\alpha})\).
- Prueba
-
La prueba del Teorema 5.31 es Ejercicio (5).
Familias de conjuntos disjuntos por pares
En la Sección 5.2, definimos dos conjuntos\(A\) y\(B\) ser disjuntos siempre que eso\(A \cap B = \emptyset\). De manera similar, si\(\Lambda\) es un conjunto de indexación no vacío y\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) es una familia de conjuntos indexados, podemos decir que esta familia de conjuntos indexados es disjunta siempre que\(\bigcap_{\alpha \in \Lambda}^{} A_{\alpha} = \emptyset\). Sin embargo, podemos usar el concepto de dos conjuntos disjuntos para definir un tipo de “desarticulación” algo más interesante para una familia de conjuntos indexados.
Dejar\(\Lambda\) ser un conjunto de indexación no vacío, y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia indexada de conjuntos. Decimos que\(\mathcal{A}\) es par sabio disjunta siempre que para todos\(\alpha\) y\(\beta\) en\(\Lambda\), si\(A_{\alpha} \ne A_{\beta}\), entonces\(A_{\alpha} \cap A_{\beta} = \emptyset\).
La Figura 5.7 muestra dos familias de conjuntos,
\(\mathcal{A} = \){\(A_1\),\(A_2\),\(A_3\),\(A_4\)} y\(\mathcal{B} = \) {\(B_1\),\(B_2\),\(B_3\),\(B_4\)}.
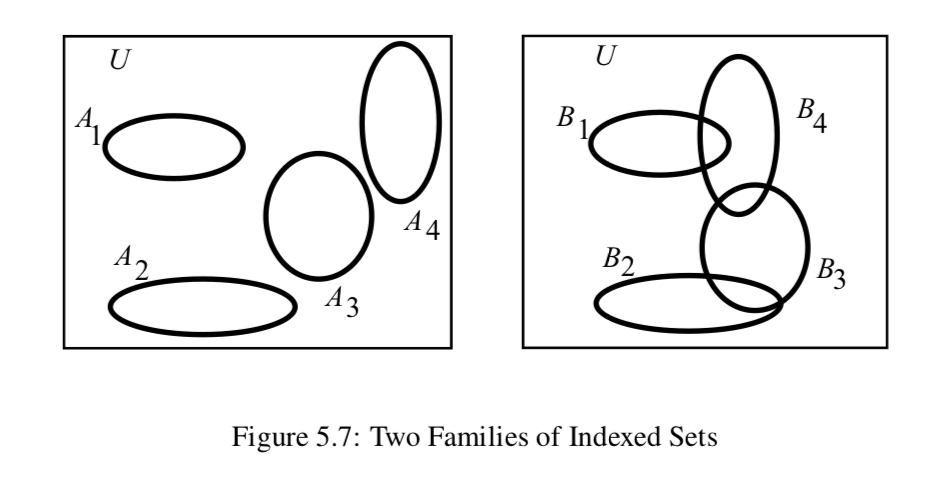
- ¿La familia de conjuntos es\(\mathcal{A}\) una familia disjunta de conjuntos? ¿Una familia disjunta de conjuntos por pares?
- ¿La familia de conjuntos es\(\mathcal{B}\) una familia disjunta de conjuntos? ¿Una familia disjunta de conjuntos por pares?
Ahora que lo universal sea\(\mathbb{R}\). Para cada uno\(n \in \mathbb{N}\), vamos\(C_n =\ (n, \infty)\), y vamos\(\mathcal{C} = \{C_n\ |\ n \in \mathbb{N}\}\). - ¿La familia de conjuntos es\(\mathcal{C}\) una familia disjunta de conjuntos? ¿Una familia disjunta de conjuntos por pares?
- Contestar
-
Agrega textos aquí. No borre primero este texto.
- Por cada número natural\(n\), vamos\(A_n = \{n, n + 1, n + 2, n + 3\}\). Utilice el método de lista para especificar cada uno de los siguientes conjuntos:
(a)\(\bigcap_{j = 1}^{3} A_j\)
(b)\(\bigcup_{j = 1}^{3} A_j\)
(c)\(\bigcap_{j = 3}^{7} A_j\)
(d)\(\bigcup_{j = 3}^{7} A_j\)
(e)\(A_9 \cap (\bigcup_{j = 3}^{7} A_j)\)
(f)\(\bigcup_{j = 3}^{7} (A_9 \cap A_j)\) - Por cada número natural\(n\), vamos\(A_n = \{k \in \mathbb{N}\ |\ k \ge n\}\). Utilice el método roster o la notación del generador de conjuntos para especificar cada uno de los siguientes conjuntos:
\(\bigcap_{j = 1}^{5} A_j\)
(a) (b)\((\bigcap_{j = 1}^{5} A_j)^c\)
(c)\(\bigcap_{j = 1}^{5} A_j ^c\)
(d)\(\bigcup_{j = 1}^{5} A_j ^c\)
(e)\(\bigcup_{j = 1}^{5} A_j\)
(f) \((\bigcup_{j = 1}^{5} A_j)^c\)
g\(\bigcap_{j \in \mathbb{N}^{} A_j\)
) h\(\bigcup_{j \in \mathbb{N}^{} A_j\) - Para cada número real positivo\(r\), defina\(T_r\) que sea el intervalo cerrado\([-r^2, r^2]\). Eso es
\[T_r = \{x \in \mathbb{R}\ |\ -r^2 \le x \le r^2\}.\]
Let\(\wedge = \{m \in \mathbb{N}\ |\ 1 \le m \le 10\}\). Use notación de intervalo o notación de generador de conjuntos para especificar cada uno de los siguientes conjuntos:
(a)\(\bigcup_{k \in \wedge}^{} T_k\)
(b)\(\bigcap_{k \in \wedge}^{} T_k\)
(c)\(\bigcup_{r \in \mathbb{R}^+}^{} T_k\)
(d)\(\bigcap_{r \in \mathbb{R}^+}^{} T_k\)
(e)\(\bigcup_{r \in \mathbb{N}}^{} T_k\)
f)\(\bigcap_{r \in \mathbb{N}}^{} T_k\) - Probar Partes (2) y (4) del Teorema 5.30. Dejar\(\Lambda\) ser un conjunto de indexación no vacío y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia de conjuntos indexados.
(a) Para cada uno\(\beta \in \Lambda\),\(A_{\beta} \subseteq \bigcup_{\alpha \in \Lambda}^{} A_{\alpha}\).
b)\((\bigcup_{\alpha \in \Lambda}^{} A_{\alpha})^c = \bigcap_{\alpha \in \Lambda}^{} A_{\alpha} ^c\) - Demostrar Teorema 5.31. Dejar\(\Lambda\) ser un conjunto de indexación no vacío, dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia indexada de conjuntos, y dejar\(B\) ser un conjunto. Después
(a)\(B \cap (\bigcup_{\alpha \in \Lambda}^{} A_{\alpha}) = \bigcup_{\alpha \in \Lambda}^{} (B \cap A_{\alpha})\), y
(b)\(B \cup (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha}) = \bigcap_{\alpha \in \Lambda}^{} (B \cup A_{\alpha})\). - Let\(\Lambda\) y\(\Gamma\) ser conjuntos de indexación no vacíos y let\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) y\(\mathcal{B} = \{B_{\beta}\ |\ \beta \in \Gamma\}\) ser indexados familias de conjuntos. Utilizar las leyes distributivas en el Ejercicio (5) para:
(a) Escribir\ ((\ bigcup_ {\ alpha\ in\ Lambda} ^ {} A_ {\ alpha})\ cap (\ bigcup_ {\ beta\ in\ Gamma} ^ {} B_ {\ beta}) como una unión de intersecciones de dos conjuntos.
(b) Escribe\ ((\ bigcap_ {\ alpha\ in\ Lambda} ^ {} A_ {\ alpha})\ cup (\ bigcap_ {\ beta\ in\ Gamma} ^ {} B_ {\ beta}) como una unión de intersecciones de dos conjuntos. - Dejar\(\Lambda\) ser un conjunto de indexación no vacío y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia de conjuntos indexados. También, supongamos que\(\Gamma \subseteq \Lambda\) y\(\Gamma \ne \emptyset\). (Nota: La letra\(\Gamma\) es la letra griega mayúscula gamma.) Demostrar que
(a)\(\bigcup_{\alpha \in \Gamma}^{} A_{\alpha} \subseteq \bigcup_{\alpha \in \Lambda}^{} A_{\alpha}\)
(b)\(\bigcap_{\alpha \in \Lambda}^{} A_{\alpha} \subseteq \bigcap_{\alpha \in \Gamma}^{} A_{\alpha}\) - Dejar\(\Lambda\) ser un conjunto de indexación no vacío y dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia de conjuntos indexados.
(a) Demostrar que si\(B\) es un conjunto tal que\(B \subseteq A_{\alpha}\) para cada\(\alpha \in \Lambda\), entonces\(B \subseteq \bigcap_{\alpha \in \Lambda}^{} A_{\alpha}\).
b) Demostrar que si\(C\) es un conjunto tal que\(A_{\alpha} \subseteq C\) para cada\(\alpha \in \Lambda\), entonces\(\bigcap_{\alpha \in \Lambda}^{} A_{\alpha} \subseteq C\). - Por cada número natural\(n\), vamos\(A_n = \{x \in \mathbb{R}\ |\ n - 1 < x < n\}\). Demostrar que\(\{A_n\ |\ n \in \mathbb{N}\}\) es una familia disjunta por pares de conjuntos y eso\(\bigcup_{n \in \mathbb{N}}^{} A_n = (\mathbb{R} ^{+} - \mathbb{N})\).
- Por cada número natural\(n\), vamos\(A_n = \{k \in \mathbb{N}\ |\ k \ge n\}\). Determinar si las siguientes afirmaciones son verdaderas o falsas. Justificar cada conclusión.
(a) Para todos\(j, k \in \mathbb{N}\), si\(j \ne k\), entonces\(A_j \cap A_k \ne \emptyset\).
b)\(\bigcap_{k \in \mathbb{N}}^{} A_k = \emptyset\). - Dé un ejemplo de una familia indexada de conjuntos\(\{A_n\ |\ n \in \mathbb{N}\}\) tal que las tres de las siguientes condiciones sean verdaderas:
(i) Para cada uno\(m \in \mathbb{N}\),\(A_m \subseteq (0,1)\);
(ii) Para cada uno\(j, k \in \mathbb{N}\), si\(j \ne k\), entonces\(A_j \cap A_k \ne \emptyset\); y
(iii)\(\bigcap_{k \in \mathbb{N}}^{} A_k = \emptyset\). - Dejar\(\Lambda\) ser un conjunto de indexación no vacío, dejar\(\mathcal{A} = \{A_{\alpha}\ |\ \alpha \in \Lambda\}\) ser una familia indexada de conjuntos, y dejar\(B\) ser un conjunto. Utilizar los resultados del Teorema 5.30 y del Teorema 5.31 para probar cada uno de los siguientes:
(a)\((\bigcup_{\alpha \in \Lambda}^{} A_{\alpha}) - B = \bigcup_{\alpha \in \Lambda}^{} (A_{\alpha} - B)\)
(b)\((\bigcap_{\alpha \in \Lambda}^{} A_{\alpha}) - B = \bigcap_{\alpha \in \Lambda}^{} (A_{\alpha} - B)\)
(c)\(B - (\bigcup_{\alpha \in \Lambda}^{} A_{\alpha}) = \bigcap_{\alpha \in \Lambda}^{} B - (A_{\alpha})\)
(d)\(B - (\bigcap_{\alpha \in \Lambda}^{} A_{\alpha}) = \bigcup_{\alpha \in \Lambda}^{} B - (A_{\alpha})\)
Exploraciones y Actividades - Una Familia Indexada de Subconjuntos del Plano Cartesiano. Dejar\(\mathbb{R} ^{\ast}\) ser el conjunto de números reales no negativos, y para cada uno\(r \in \mathbb{R} ^{\ast}\), dejar
\[\begin{array} {rcl} {C_r} &= & {\{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 = r^2\}} \\ {D_r} &= & {\{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 \le r^2\}} \\ {T_r} &= & {\{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 > r^2\} = D_r ^c.} \end{array}\]Si\(r > 0\), entonces el conjunto\(C_r\) es el círculo de radio\(r\) con centro en el origen como se muestra en la Figura 5.8, y el conjunto\(D_r\) es el disco sombreado (incluyendo el límite) que se muestra en la Figura 5.8.
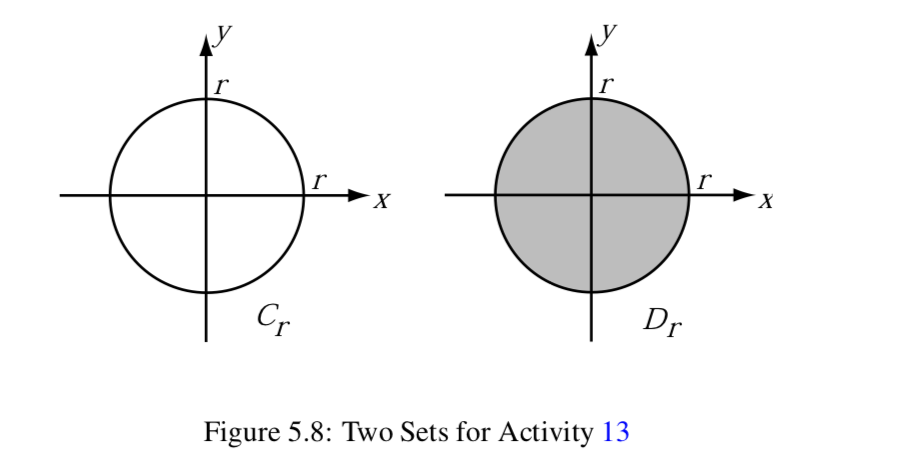
(a) Determinar\(\bigcup_{r \in \mathbb{R} ^{\ast}}^{} C_r\) y\(\bigcap_{r \in \mathbb{R} ^{\ast}}^{} C_r\)
(b) Determinar\(\bigcup_{r \in \mathbb{R} ^{\ast}}^{} D_r\) y\(\bigcap_{r \in \mathbb{R} ^{\ast}}^{} D_r\)
(c) Determinar\(\bigcup_{r \in \mathbb{R} ^{\ast}}^{} T_r\) y\(\bigcap_{r \in \mathbb{R} ^{\ast}}^{} T_r\)
(d) Dejar\(\mathcal{C} = \{C_r\ |\ r \in \mathbb{R} ^{\ast}\}\)\(\mathcal{D} = \{D_r\ |\ r \in \mathbb{R} ^{\ast}\}\), y\(\mathcal{T} = \{T_r\ |\ r \in \mathbb{R} ^{\ast}\}\) . ¿Alguna de estas familias indexadas de conjuntos por pares es disjunta? Explique.
Ahora deja\(I\) ser el intervalo cerrado [0, 2] y dejar\(J\) ser el intervalo cerrado [1, 2].
(e) Determinar\(\bigcup_{r \in I}^{} C_r\)\(\bigcap_{r \in I}^{} C_r\),\(\bigcup_{r \in J}^{} C_r\),, y\(\bigcap_{r \in J}^{} C_r\)
(f) Determinar\(\bigcup_{r \in I}^{} D_r\)\(\bigcap_{r \in I}^{} D_r\),\(\bigcup_{r \in J}^{} D_r\), y\(\bigcap_{r \in J}^{} D_r\)
(g) Determinar\((\bigcup_{r \in I}^{} D_r)^c\),\((\bigcap_{r \in I}^{} D_r)^c\)\((\bigcup_{r \in J}^{} D_r)^c\), y\((bigcap_{r \in J}^{} D_r)^c\)
(h) Determinar \(\bigcup_{r \in I}^{} T_r\),\(\bigcap_{r \in I}^{} T_r\)\(\bigcup_{r \in J}^{} T_r\), e i\(\bigcap_{r \in J}^{} T_r\)
) Usa las Leyes de De Morgan para explicar la relación entre tus respuestas en las Partes (13g) y (13h).
- Contestar
-
Agrega textos aquí. No borre primero este texto.


