6.6: Funciones que actúan sobre conjuntos
- Page ID
- 116101
Vista previa de la Actividad 1 (Funciones y Conjuntos)
Dejar\(S = \{a, b, c, d\}\) y\(T = \{s, t, u\}\). Definir\(f: S \to T\) por
\(f(a) = s\)\(f(b) = t\)\(f(c) = t\)\(f(d) = s\)
- Dejar\(A = \{a, c\}\) y\(B = \{a, d\}\). Observe que\(A\) y\(B\) son subconjuntos de\(S\). Utilice el método roster para especificar los elementos de los dos subconjuntos siguientes de\(T\):
(a)\(\{f(x)\ |\ x \in A\}\)
(b)\(\{f(x)\ |\ x \in B\}\) - Dejar\(C = \{s, t\}\) y\(D = \{s, u\}\). Observe que\(C\) y\(D\) son subconjuntos de\(T\). Utilice el método roster para especificar los elementos de los siguientes dos subconjuntos de\(S\):
(a)\(\{x \in S\ |\ f(x) \in C\}\)
(b)\(\{x \in S\ |\ f(x) \in D\}\)
Ahora deja\(g: \mathbb{R} \to \mathbb{R}\) ser definido por\(g(x) = x^2\), para cada uno\(x \in \mathbb{R}\). - Vamos\(A = \{1, 2, 3, -1\}\). Utilice el método roster para especificar los elementos del conjunto\(\{g(x)\ |\ x \in A\}\).
- Utilice el método roster para especificar los elementos de cada uno de los siguientes conjuntos:
(a)\(\{x \in \mathbb{R}\ |\ g(x) = 1\}\)
(b)\(\{x \in \mathbb{R}\ |\ g(x) = 9\}\)
(c)\(\{x \in \mathbb{R}\ |\ g(x) = 15\}\)
(d)\(\{x \in \mathbb{R}\ |\ g(x) = -1\}\) - Vamos\(B = \{1, 9, 15, -1\}\). Utilice el método roster para especificar los elementos del conjunto
\ {\ x\ in\ mathbb {R}\ |\ g (x)\ in B\}\).
Vista previa Actividad 2 (Funciones e Intervalos)
Dejar\(g: \mathbb{R} \to \mathbb{R}\) ser definido por\(g(x) = x^2\), para cada uno\(x \in \mathbb{R}\).
- Primero determinaremos dónde g mapea el intervalo cerrado [1, 2]. (Recordemos eso\([1, 2] = \{x \in R\ |\ 1 \le x \le 2\}\).) Es decir, describiremos, en términos más simples, el conjunto\(\{g(x)\ |\ x \in [1, 2]\}\). Este es el conjunto de todas las imágenes de los números reales en el intervalo cerrado [1, 2].
(a) Dibujar una gráfica de la función\(g\) utilizando\(-3 \le x \le 3\).
(b) En la gráfica, dibuje las líneas verticales\(x = 1\) y\(x = 2\) del eje x a la gráfica. Etiquetar los puntos\(P(1, f(1))\) y\(Q(2, f (2))\) en la gráfica.
(c) Ahora dibuje líneas horizontales desde los puntos\(P\) y\(Q\) hasta el eje y. Utilice esta información de la gráfica para describir el conjunto\(\{g(x)\ |\ x \in [1, 2]\}\) en términos más simples. Utilice notación de intervalo o notación de generador de conjuntos. - Ahora determinaremos todos los números reales que g mapea en el intervalo cerrado [1, 4]. Es decir, describiremos el conjunto\(\{x \in \mathbb{R}\ |\ g(x) \in [1, 4]\}\) en términos más simples. Este es el conjunto de todas las preimágenes de los números reales en el intervalo cerrado [1, 4].
(a) Dibujar una gráfica de la función\(g\) utilizando\(-3 \le x \le 3\).
(b) En la gráfica, dibuje las líneas horizontales\(y = 1\) y\(y = 4\) de su eje a la gráfica. Etiquetar todos los puntos donde estas dos líneas se cruzan con la gráfica.
(c) Ahora dibuje líneas verticales desde los puntos de la Parte (2) hasta el eje x, y luego use la información resultante para describir el conjunto\(\{x \in \mathbb{R}\ |\ g(x) \in [1, 4]\}\) en términos más simples. (Deberá describir este conjunto como una unión de dos intervalos. Utilice notación de intervalo o notación de generador de conjuntos.)
Funciones que actúan sobre conjuntos
En nuestro estudio de funciones, nos hemos centrado en cómo una función “mapea” elementos individuales de su dominio al codominio. También se estudió la preimagen de un elemento individual en su codominio. Por ejemplo, si\(f: \mathbb{R} \to \mathbb{R}\) se define por\(f(x) = x^2\), para cada uno\(x \in \mathbb{R}\), entonces
- \(f(2) = 4\). Decimos que los\(f\) mapas 2 a 4 o que 4 es la imagen de 2 bajo la función\(f\).
- Ya que\(f(2) = 4\) implica eso\(x = 2\) o\(x = -2\), decimos que las preimágenes de 4 son 2 y -2 o que el conjunto de preimágenes de 4 es {-2, 2}.
Para una función\(f: S \to T\), el siguiente paso es considerar subconjuntos de\(S\) o\(T\) y qué les corresponde en el otro conjunto. Esto lo hicimos en las Actividades de Vista Previa. Daremos algunas definiciones y luego revisaremos los ejemplos en la Vista previa de Actividades a la luz de estas definiciones. Primero consideraremos la situación donde\(A\) se encuentra un subconjunto de\(S\) y consideraremos el conjunto de salidas de cuyas entradas son de\(A\). Este será un subconjunto de\(T\).
Vamos\(f: S \to T\). Si\(A \subseteq S\), entonces la imagen de\(A\) debajo\(f\) es el conjunto\(f(A)\), donde
\(f(A) = \{f(x)\ |\ x \in A\}\).
Si no hay confusión en cuanto a qué función se está utilizando, llamamos a\(f(A)\) la imagen de\(A\).
Consideramos ahora la situación en la que\(C\) se encuentra un subconjunto de\(T\) y consideramos el subconjunto de\(A\) que consiste en todos los elementos de\(T\) cuyos resultados se encuentran en\(C\).
Vamos\(f: S \to T\). Si\(C \subseteq T\), entonces la preimagen de\(C\) bajo\(f\) es el conjunto\(f^{-1}(C)\), donde
\(f^{-1}(C) = \{x \in S\ |\ f(x) \in C\}\).
Si no hay confusión en cuanto a qué función se está utilizando, llamamos a\(f^{-1}(C)\) la preimagen de\(C\). La preimagen del conjunto\(C\) bajo también\(f\) se llama la imagen inversa de\(C\) bajo\(f\).
Observe que el conjunto\(f^{-1}(C)\) se define si\(f^{-1}\) es o no una función.
Dejar\(S = \{a, b, c, d\}\) y\(T = \{s, t, u\}\). Definir\(f: S \to T\) por
\(f(a) = s\)\(f(b) = t\)\(f(c) = t\)\(f(d) = s\).
Vamos\(A = \{a, c\}\),\(B = \{a, d\}\),\(C = \{s, t\}\), y\(D=\{s, u\}\).
Usa tu trabajo en Vista previa de Actividad\(\PageIndex{1}\) para determinar cada uno de los siguientes conjuntos:
- \(f(A)\)
- \(f(B)\)
- \(f^{-1}(C)\)
- \(f^{-1}(D)\)
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Dejar\(g: \mathbb{R} \to \mathbb{R}\) ser definido por\(g(x) = x^2\), para cada uno\(x \in \mathbb{R}\). Los siguientes resultados se basan en los ejemplos de Vista previa de la actividad\(\PageIndex{1}\) y Vista previa de la actividad\(\PageIndex{2}\).
- Vamos\(A = \{1, 2, 3, -1\}\). Entonces\(f(A) = \{1, 4, 9\}\).
- Vamos\(B = \{1, 9 ,15, -1\}\). Entonces\(f^{-1}(B) = \{-\sqrt{15}, -3, -1, 1, 3, \sqrt{15}\}\).
Las gráficas de la Actividad de Vista Previa\(\PageIndex{2}\) ilustran los siguientes resultados:
- Si\(T\) es el intervalo cerrado [1, 2], entonces la imagen del conjunto\(T\) es
\[\begin{array} {rcl} {f(T)} &= & {\{f(x)\ |\ x \in [1, 2]\}} \\ {} &= & {[1, 4].} \end{array}\] - Si\(C\) es el intervalo cerrado [1, 4], entonces la preimagen del conjunto\(C\) es
\[f^{-1}(C) = \{x \in \mathbb{R}\ |\ f(x) \in [1, 4]\} = [-2, -1] \cup [1, 2].\]
Operaciones de conjunto y funciones que actúan sobre conjuntos
Consideraremos ahora la siguiente situación: Let\(S\) and\(T\) be sets y let f be a function from\(S\) to\(T\). También, dejar\(A\) y\(B\) ser subconjuntos de\(S\) y dejar\(C\) y\(D\) ser subconjuntos de\(T\). En lo que resta de esta sección, consideraremos las siguientes situaciones y responderemos a las preguntas que se planteen en cada caso.
- El conjunto\(A \cap B\) es un subconjunto de\(S\) y por lo tanto\(f(A \cap B\) es un subconjunto de\(T\). Además,\(f(A)\) y\(f(B)\) son subconjuntos de\(T\). De ahí,\(f(A) \cap f(B)\) es un subconjunto de\(T\).
¿Existe alguna relación entre\(f(A \cap B\) y\(f(A) \cap f(B)\)? - El conjunto\(A \cup B\) es un subconjunto de\(S\) y por lo tanto\(f(A \cup B\) es un subconjunto de\(T\). Además,\(f(A)\) y\(f(B)\) son subconjuntos de\(T\). De ahí,\(f(A) \cup f(B)\) es un subconjunto de\(T\).
¿Existe alguna relación entre\(f(A \cup B\) y\(f(A) \cup f(B)\)? - El conjunto\(C \cap D\) es un subconjunto de\(T\) y por lo tanto\(f^{-1}(C \cap D)\) es un subconjunto de\(S\). Además,\(f^{-1}(C)\) y\(f^{-1}(D)\) son subconjuntos de\(S\). De ahí,\(f^{-1}(C) \cap f^{-1}(D)\) es un subconjunto de\(S\).
¿Existe alguna relación entre los conjuntos\(f^{-1}(C \cap D)\) y\(f^{-1}(C) \cap f^{-1}(D)\)? - El conjunto\(C \cup D\) es un subconjunto de\(T\) y por lo tanto\(f^{-1}(C \cup D)\) es un subconjunto de\(S\). Además,\(f^{-1}(C)\) y\(f^{-1}(D)\) son subconjuntos de\(S\). De ahí,\(f^{-1}(C) \cup f^{-1}(D)\) es un subconjunto de\(S\).
¿Existe alguna relación entre los conjuntos\(f^{-1}(C \cup D)\) y\(f^{-1}(C) \cup f^{-1}(D)\)?
Estas y otras preguntas serán exploradas en la próxima comprobación de progreso.
En la Sección 6.2, introdujimos funciones que involucran congruencias. Por ejemplo, si dejamos
\(\mathbb{Z}_8 = \{0, 1, 2, 3, 4, 5, 6, 7\}.\)
entonces podemos definir\(f: \mathbb{Z}_8 \to \mathbb{Z}_8\) por\(f(x) = r\), donde\((x^2 + 2) \equiv r\) (mod 8) y\(r \in \mathbb{Z}_8\). Además, acortamos esta notación a
\(f(x) = (x^2 + 2)\)(mod 8)
Utilizaremos los siguientes subconjuntos de\(\mathbb{Z}_8\):
\(A = \{1, 2, 4\}\)\(B = \{3, 4, 6\}\)\(C = \{1, 2, 3\}\)\(D = \{3, 4, 5\}\)
- Verificar que\(f(0) = 2\),\(f(1) = 3\),\(f(2) = 6\), y\(f(3) = 3\). Después determinar\(f(4)\),\(f(5)\),\(f(6)\) y\(f(7)\).
- Determinar\(f(A)\),\(F=f(A=B)\),\(f^{-1}(C)\), y\(f^{-1}(D)\).
- Para cada uno de los siguientes, determine los dos subconjuntos de\(\mathbb{Z}_8\) y luego determine si existe una relación entre los dos conjuntos. Por ejemplo,\(A \cap B = \{4\}\) y desde entonces\(f(4) = 2\), vemos eso\(f(A \cap B) = \{2\}\).
a)\(f(A \cap B)\) y\(f(A) \cap f(B)\)
b)\(f(A \cup B)\) y\(f(A) \cup f(B)\)
c)\(f^{-1}(C \cap D)\) y\(f^{-1}(C) \cap f^{-1}(D)\)
d)\(f^{-1}(C \cup D)\) y\(f^{-1}(C) \cup f^{-1}(D)\) - Observe que\(f(A)\) es un subconjunto del codominio,\(\mathbb{Z}_8\). En consecuencia,\(f^{-1}(f(A))\) es un subconjunto del dominio,\(\mathbb{Z}_8\). ¿Hay alguna relación entre\(A\) y\(f^{-1}f(A))\) en este caso?
- Observe que\(f^{-1}(C)\) es un subconjunto del codominio,\(\mathbb{Z}_8\). En consecuencia,\(f(f^{-1}(f(C))\) es un subconjunto del dominio,\(\mathbb{Z}_8\). ¿Hay alguna relación entre\(C\) y\(f(f^{-1}f(C))\) en este caso?
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Definir\(f: \mathbb{R} \to \mathbb{R}\) por\(f(x) = x^2 + 2\) para todos\(x \in \mathbb{R}\). Será útil utilizar la gráfica que se muestra en la Figura 6.11.
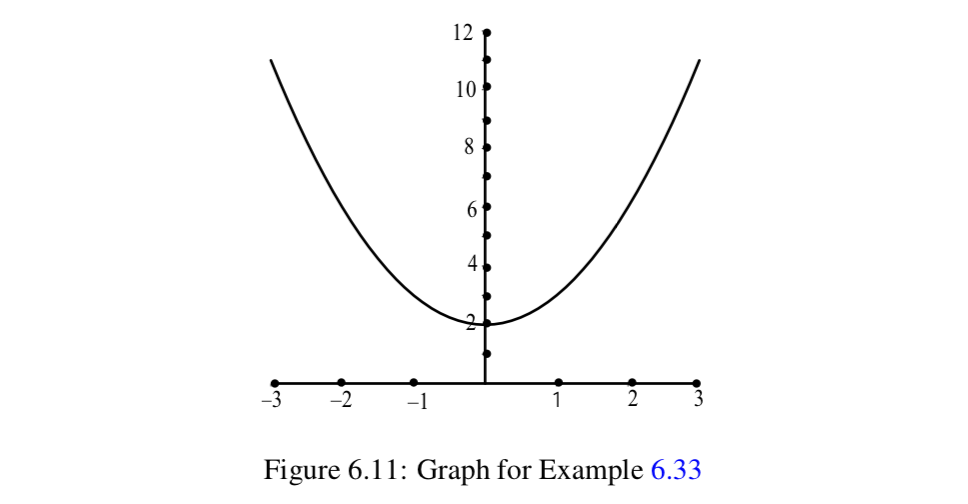
Utilizaremos los siguientes intervalos cerrados:
\(A = [0, 3]\)\(B = [-2, 1]\)\(C = [2, 6]\)\(D = [0, 3]\).
- Verificar eso\(f(A) = [2, 11]\),\(f(B) = [2, 6]\),\(f^{-1}(C) = [-2, 2]\), y eso\(f^{-1}(D) = [-1, 1]\).
- a) Explicar por qué\(f(A \cap B) = [2, 3]\) y\(f(A) \cap f(B) = [2, 6]\). Entonces en este caso,\(f(A \cap B) \subseteq f(A) \cap f(B)\).
b) Explicar por qué\(f(A \cup B) = [2, 11]\) y\(f(A) \cup f(B) = [2, 11]\). Entonces en este caso,\(f(A \cup B) \subseteq f(A) \cup f(B)\).
c) Explicar por qué\(f^{-1}(C \cap D) = [-1, 1]\) y\(f^{-1}(C) \cap f^{-1}(D) = [-1, 1]\). Entonces en este caso,\(f^{-1}(C \cap D) \subseteq f^{-1}(C) \cap f^{-1}(D)\).
d) Explicar por qué\(f^{-1}(C \cup D) = [-2, 2]\) y\(f^{-1}(C) \cap f^{-1}(D) = [-2, 2]\). Entonces en este caso,\(f^{-1}(C \cup D) \subseteq f^{-1}(C) \cup f^{-1}(D)\). - Reacll eso\(A = [0, 3]\). \(f(A) = [2, 11]\)El aviso es un subconjunto del codominio,\(\mathbb{R}\). Explique por qué\(f^{-1}(f(A)) = [-3, 3]\). Ya que\(f^{-1}f(A))\) es un subconjunto del dominio\(\mathbb{R}\),, vemos que en este caso,\(A \subseteq f^{-1}(f(A))\).
- Reacll eso\(C = [2, 6]\). \(f^{-1}(C) = [-2, 2]\)El aviso es un subconjunto del codominio,\(\mathbb{R}\). Explique por qué\(f(f^{-1}f(C)) = [2, 6]\). Ya que\(f^{-1}f(C))\) es un subconjunto del dominio\(\mathbb{R}\),, vemos que en este caso,\(f(f^{-1}(C)) = C\).
Los ejemplos en Progress Check 6.32 y Ejemplo 6.33 tenían como objetivo ilustrar resultados generales sobre cómo actúan las funciones en los conjuntos. En particular, investigamos cómo la acción de una función sobre conjuntos interactúa con las operaciones de conjunto de intersección y unión. Ahora vamos a exponer los teoremas que estos ejemplos estaban destinados a ilustrar. Algunas de las pruebas se dejarán como ejercicios.
Dejar\(f: S \to T\) ser una función y dejar\(A\) y\(B\) ser subconjuntos de\(S\). Entonces
- \(f(A \cap B\)\ subseteq f (A)\ cap f (B)\)
- \(f(A \cup B\)= f (A)\ copa f (B)\)
- Prueba
-
Demostraremos la Parte (1). El comprobante de la Parte (2) es Ejercicio (5).
Supongamos que\(f: S \to T\) es una función y dejar\(A\) y\(B\) ser subconjuntos de\(S\). Vamos a probar que\(f(A \cap B\)\ subseteq f (A)\ cap f (B)\) demostrando que para todos\(y \in T\), si\(y \in f(A \cap B)\), entonces\(y \in f(A) \cap f(B)\).
Eso lo asumimos\(y \in f(A \cap B)\). Esto quiere decir que existe\(x \in A \cap B\) tal que\(f(x) = y\). Ya que\(x \in A \cap B\), concluimos que\(x \in A\) y\(x \in B\).
- Desde\(x \in A\) y\(f(x) = y\), concluimos que\(y \in f(A)\).
- Desde\(x \in B\) y\(f(x) = y\), concluimos que\(y \in f(B)\).
Desde\(x \in f(A)\) y\(y \in f(B)\),\(y \in f(A) \cap f(B)\). Esto prueba que si\(y \in f(A \cap B)\), entonces\(y \in f(A) \cap f(B)\). De ahí\(f(A \cap B\)\ subseteq f (A)\ cap f (B)\).
Dejar\(f: S \to T\) ser una función y dejar\(C\) y\(D\) ser subconjuntos de\(T\). Entonces
- \(f^{-1}(C \cap D) = f^{-1}(C) \cap f^{-1}(D)\)
- \(f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)\)
- Prueba
-
Demostraremos la Parte (2). El comprobante de la Parte (1) es Ejercicio (6).
Supongamos que\(f: S \to T\) es una función y que\(C\) y\(D\) son subconjuntos de\(T\). Lo demostraremos\(f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)\) demostrando que cada conjunto es un subconjunto del otro.
Empezamos por dejar\(x\) ser un elemento de\(f^{-1}(C \cup D)\). Esto significa que\(f(x)\) es un elemento de\(C \cup D\). Por lo tanto,
\(f(x) \in C\)o\(f(x) \in D\)
En el caso donde\(f(x) \in C\), concluimos eso\(x \in f^{-1}(C)\), y de ahí eso\(x \in f^{-1}(C) \cup f^{-1}(D)\). En el caso donde\(f(x) \in D\), vemos eso\(x \in f^{-1}(D)\), y de ahí eso\(x \in f^{-1}(C) \cup f^{-1}(D)\). Entonces en ambos casos\(x \in f^{-1}(C) \cup f^{-1}(D)\),, y hemos demostrado que\(f^{-1}(C \cup D) \subseteq f^{-1}(C) \cup f^{-1}(D)\)
Ahora vamos\(t \in f^{-1}(C) \cup f^{-1}(D)\). Esto significa que
\(t \in f^{-1}(C)\)o\(t \in f^{-1}(D)\)
- En el caso donde\(t \in f^{-1}(C)\), concluimos eso\(f(t) \in C\) y por lo tanto eso\(f(t) \in C \cup D\). Esto significa que\(t \in f^{-1}(C \cup D)\).
- De igual manera, cuando\(t \in f^{-1}(D)\), se deduce eso\(f(t) \in D\) y de ahí aquello\(f(t) \in C \cup D\). Esto significa que\(t \in f^{-1}(C \cup D)\).
Estos dos casos prueban que si\(t \in f^{-1}(C) \cup f^{-1}(D)\), entonces\(t \in f^{-1}(C \cup D)\). Por lo tanto,\(f^{-1}(C) \cup f^{-1}(D) \subseteq f^{-1}(C \cup D)\).
Dado que ahora hemos demostrado que cada uno de los dos conjuntos es un subconjunto del otro conjunto, podemos concluir que\(f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)\).
Dejar\(f: S \to T\) ser una función y dejar\(A\) ser un subconjunto de\(S\) y dejar\(C\) ser un subconjunto de\(T\). Entonces
- \(A \subseteq f^{-1}(f(A))\)
- \(f(f^{-1}(C)) \subseteq C\)
- Prueba
-
Demostraremos la Parte (1). El comprobante de la Parte (2) es Ejercicio (7).
Para probar la Parte (1), lo probaremos para todos\(a \in S\), si\(a \in A\), entonces\(a \in f^{-1}(f(A))\). Así que vamos\(a \in A\). Entonces, por definición,\(f(a) \in f(A)\). Eso lo sabemos\(f(A) \subseteq T\), y así\(f^{-1}(f(A)) \subseteq S\). Observe que
\(f^{-1}(f(A)) = \{x \in S\ |\ f(x) \in f(A)\}.\)
Ya que\(f(a) \in f(A)\), usamos esto para concluir que\(a \in f^{-1}(f(A)). This proves that if \(a \in A\), entonces\(a \in f^{-1}(f(A))\), y de ahí que\(A \in f^{-1}(f(A))\)
- Let\(f: S \to T\). let\(A\) y\(B\) ser subconjuntos de\(S\), y let\(C\) y\(D\) ser subconjuntos de\(T\). Porque\(x \in S\) y\(y \in T\), explique cuidadosamente lo que significa decir que
a\(y \in f(A \cap B)\)
)\(y \in f(A \cup B)\)
b)\(y \in f(A )\cap f(B)\)
c) d\(y \in f(A )\cup f(B)\)
) e\(x \in f^{-1}(C \cap D)\)
) f \(x \in f^{-1}(C \cup D)\)
g\(x \in f^{-1}(C) \cap f^{-1}(D)\)
) h\(x \in f^{-1}(C) \cup f^{-1}(D)\) - Dejar\(f: \mathbb{R} \to \mathbb{R}\) pasar\(f(x) = -2x + 1\). Vamos
\(A = [2, 5]\)\(B = [-1, 3]\)\(C = [-2, 3]\)\(D = [1, 4]\).
Encuentre cada uno de los siguientes: a
\(f(A)\)
)\(f^{-1}(f(A))\)
b) c\(f^{-1}(C)\)
) d\(f(f^{-1}(C))\)
) e\(f(A \cap B)\)
) f)\(f(A )\cap f(B)\)
g\(f^{-1}(C \cap D)\)
) h\(f^{-1}(C) \cap f^{-1}(D)\) - Dejar pasar\(g: \mathbb{N} \times \mathbb{N} \to \mathbb{N}\)\(g(m, n) = 2^m 3^n\), dejar\(A = \{1, 2, 3\}\), y dejar\(C = \{1, 4, 6, 9, 12, 16, 18\}\). Buscar
(a)\(g(A \times A)\)
(b)\(g^{-1}(C)\)
(c)\(g^{-1}(g(A \times A))\)
(d)\(g(g^{-1}(C))\) - (a) Dejar\(S = \{1, 2, 3, 4\}\). Definir\(F: S \to \mathbb{N}\) por\(F(x) = x^2\) para cada uno\(x \in s\). ¿Cuál es el rango de la función\(F\) y qué es\(F(S)\)? ¿Cómo se comparan estos dos conjuntos?
Ahora dejar\(A\) y\(B\) ser conjuntos y dejar\(f: A \to B\) ser una función arbitraria de\(A\) a\(B\).
b) Explique por qué\(f(A) = \text{range}(f)\).
(c) Definir una función\(g: A \to f(A)\) por\(g(x) = f(x)\) para todos\(x\) en\(A\). Demostrar que la función\(g\) es una sobrejección. - Demostrar Parte (2) del Teorema 6.34.
Dejar\(f: S \to T\) ser una función y dejar\(A\) y\(B\) ser subconjuntos de\(S\). Entonces\(f(A \cup B) = f(A) \cup f(B)\). - Demostrar Parte (1) del Teorema 6.35.
Dejar\(f: S \to T\) ser una función y dejar\(C\) y\(D\) ser subconjuntos de\(T\). Entonces\(f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)\). - Demostrar Parte (2) del Teorema 6.36.
Dejar\(f: S \to T\) ser una función y dejar\(C \subseteq T\). Entonces\(f(f^{-1}(C)) \subseteq C\). - Dejar\(f: S \to T\) y dejar\(A\) y\(B\) ser subconjuntos de\(S\). Demostrar o desacreditar cada uno de los siguientes: a
) Si\(A \subseteq B\), entonces\(f(A) \subseteq f(B)\).
b) Si\(f(A) \subseteq f(B)\), entonces\(A \subseteq B\). - Dejar\(f: S \to T\) y dejar\(C\) y\(D\) ser subconjuntos de\(T\). Demostrar o desacreditar cada uno de los siguientes: a
) Si\(C \subseteq D\), entonces\(f^{-1}(C) \subseteq f^{-1}(D)\).
b) Si\(f^{-1}(C) \subseteq f^{-1}(D)\), entonces\(C \subseteq D\). - Demostrar o desmentir:
Si\(f: S \to T\) es una función\(A\) y y\(B\) son subconjuntos de\(S\), entonces
\(f(A) \cap f(B) \subseteq f(A \cap B)\).
Nota: La Parte (1) del Teorema 6.34 establece que\(f(A \cap B) \subseteq f(A) \cap f(B)\). - Si\(f: S \to T\) es una función, let\(A \subseteq S\), y let\(C \subseteq T\).
(a) La parte (1) del Teorema 6.36 establece que\(A \subseteq f^{-1}(f(A))\). Dar un ejemplo donde\(f^{-1}(f(A)) \notsubseteq A\).
(b) La Parte (2) del Teorema 6.36 establece que\(f(f^{-1}(C)) \subseteq C\). Dar un ejemplo donde\(C \notsubseteq f(f^{-1}(C))\). - ¿La siguiente proposición es verdadera o falsa? Justifica tu conclusión con una prueba o un contraejemplo.
Si\(f: S \to T\) es una inyección y\(A \subseteq S\), entonces\(f^{-1}(f(A)) = A\). - ¿La siguiente proposición es verdadera o falsa? Justifica tu conclusión con una prueba o un contraejemplo.
Si\(f: S \to T\) es una inyección y\(C \subseteq T\), entonces\(f^{-1}(f(C)) = C\). - Dejar (f: S\ a T\). Demostrarlo\(f(A \cap B) = f(A) \cap f(B)\) para todos los subconjuntos\(A\) y\(B\) de\(S\) si y solo si\(f\) es una inyección.
- Responder
-
Agrega textos aquí. No elimine primero este texto.


