7.3: Clases de equivalencia

PREVIAR ACTIVIDAD\(\PageIndex{1}\): Sets Associated with a Relation

Como se indicó en la Sección 7.2, una relación de equivalencia en un conjunto\(A\) es una relación con una cierta combinación de propiedades (reflexivas, simétricas y transitivas) que permiten ordenar los elementos del conjunto en ciertas clases. Esto se hace por medio de ciertos subconjuntos de los\(A\) que están asociados con los elementos del conjunto\(A\). Esto se ilustrará con el siguiente ejemplo. Dejar\(A = \{a, b, c, d, e\}\), y dejar que\(R\) sea la relación sobre el conjunto\(A\) definido de la siguiente manera:

\(a\ R\ a\)\(b\ R\ b\)\(c\ R\ c\)\(d\ R\ d\)\(e\ R\ e\)
\(a\ R\ b\)\(b\ R\ a\)\(b\ R\ e\)\(e\ R\ b\)
\(a\ R\ e\)\(e\ R\ a\)\(c\ R\ d\)\(d\ R\ c\)

Para cada uno\(y \in A\), defina el subconjunto\(R[y]\) de la\(A\) siguiente manera:

\(R[y] = \{x \in A\ |\ x\ R\ y\}.\)

Es decir,\(R[y]\) consiste en esos elementos en\(A\) tal que\(x\ R\ y\). Por ejemplo, usando\(y = a\), vemos eso\(a\ R\ a\),\(b\ R\ a\), y\(e\ R\ a\), y así\(R[a] = \{a, b, e\}\).

1. Determinar\(R[b]\),\(R[c]\),\(R[d]\) y\(R[e]\).
2. Dibujar una gráfica dirigida para la relación\(R\) y explicar por qué\(R\) es una relación de equivalencia en\(A\).
3. ¿Cuáles de los conjuntos\(R[a]\),\(R[b]\),\(R[c]\),\(R[d]\) y\(R[e]\) son iguales?
4. ¿Cuáles de los conjuntos\(R[a]\)\(R[b]\),,\(R[c]\),\(R[d]\) y\(R[e]\) son disjuntos?

Como veremos en esta sección, las relaciones entre estos conjuntos son típicas para una relación de equivalencia. El siguiente ejemplo mostrará cuán diferente puede ser esto para una relación que no es una relación de equivalencia.

Dejar\(A = \{a, b, c, d\}\), y dejar que\(S\) sea la relación sobre el conjunto\(A\) definido de la siguiente manera:

\(b\ S\ b\)\(c\ S\ c\)\(d\ S\ d\)\(e\ S\ e\)
\(a\ S\ b\)\(a\ S\ d\)\(b\ S\ c\)
\(c\ S\ d\)\(d\ S\ c\)

5. Dibuja un dígrafo que represente la relación\(S\) sobre\(A\). \(S\)Explique por qué no es una relación de equivalencia sobre\(A\).

Para cada uno\(y \in A\), defina el subconjunto\(S[y]\) de la\(A\) siguiente manera:
\(S[y] = \{x \in A\ |\ x\ S\ y\} = \{x \in A\ |\ (x, y) \in S\}.\)

Por ejemplo, usando\(y = b\), vemos que\(S[b] = \{a, b\}\) desde\((a, b) \in S\) y\((b, b) \in S\). Además, vemos que\(S[a] = \emptyset\) ya que no hay x 2 A tal que.x; a/ 2 S.

6. Determinar\(S[c]\),\(S[d]\), y\(S[e]\).

7. ¿Cuáles de los conjuntos\(S[a]\)\(S[b]\),,\(S[c]\),\(S[d]\), y\(S[e]\) son iguales?

8. ¿Cuáles de los conjuntos\(S[b]\)\(S[c]\),,\(S[d]\), y\(S[e]\) son disjuntos?

PREVIAR ACTIVIDAD\(\PageIndex{2}\): Congruence Modulo 3

Una relación de equivalencia importante que hemos estudiado es el módulo de congruencia\(n\) en los enteros. También podemos definir subconjuntos de los enteros basados en el módulo de congruencia\(n\). Ilustraremos esto con congruencia módulo 3. Por ejemplo, podemos\(C[0]\) definir como el conjunto de todos los enteros a que sean congruentes a 0 módulo 3. Es decir,

\(C[0] = \{a \in \mathbb{Z}\ |\ a \equiv 0\text{ (mod 3)}\}.\)

Dado que un entero\(a\) es congruente con 0 módulo 3 si un solo si 3 se divide\(a\), podemos usar el método roster para especificar este conjunto de la siguiente manera:

\(C[0] = \{..., -9, -6, -3, 0, 3, 6, 9, ...\}.\)

1. Utilice el método roster para especificar cada uno de los siguientes conjuntos:
   
   (a) El conjunto\(C[1]\) de todos los enteros\(a\) que son congruentes a 1 módulo 3. Es decir,\(C[1] = \{a \in \mathbb{Z}\ |\ a \equiv 1 \text{ (mod 3)}\}.\)
   (b) El conjunto\(C[2]\) de todos los enteros\(a\) que son congruentes a 2 módulo 3. Es decir,\(C[2] = \{a \in \mathbb{Z}\ |\ a \equiv 2 \text{ (mod 3)}\}.\)
   (c) El conjunto\(C[3]\) de todos los enteros\(a\) que son congruentes a 3 módulo 3. Es decir,\(C[3] = \{a \in \mathbb{Z}\ |\ a \equiv 3 \text{ (mod 3)}\}.\)
2. Ahora considere los tres conjuntos,\(C[0]\),\(C[1]\), y\(C[2]\).
   
   (a) Determinar la intersección de cualquiera de estos dos conjuntos. Es decir, determinar\(C[0] \cap C[1]\),\(C[0] \cap C[2]\), y\(C[1] \cap C[2]\).
   b) Dejar\(n = 734\). ¿Cuál es el resto cuando\(n\) se divide por 3? ¿Cuál de los tres conjuntos, si los hay, contiene\(n = 734\)?
   (c) Repetir la Parte (2b) para\(n = 79\) y para\(n = -79\).
   (d) ¿Cree que\(C[0] \cup C[1] \cup C[2] = \mathbb{Z}\) Explique.
   e) ¿El conjunto es\(C[3]\) igual a uno de los conjuntos\(C[0]\)\(C[1]\), o\(C[2]\)?
   (f) También podemos definir\(C[4] = \{a \in \mathbb{Z}\ |\ a \equiv 4 \text{ (mod 3)}\}\). ¿Este conjunto es igual a alguno de los conjuntos anteriores que hemos estudiado en esta parte? Explique.

La definición de una clase de equivalencia

Hemos indicado que una relación de equivalencia en un conjunto es una relación con una cierta combinación de propiedades (reflexivas, simétricas y transitivas) que nos permiten ordenar los elementos del conjunto en ciertas clases. Vimos que esto sucedía en las actividades de vista previa. Ahora podemos ilustrar específicamente lo que esto significa. Por ejemplo, en Preview Activity\(\PageIndex{2}\), utilizamos la relación de equivalencia del módulo 3 de congruencia\(\mathbb{Z}\) para construir los siguientes tres conjuntos:

\[\begin{array} {rcl} {C[0]} &= & {\{a \in \mathbb{Z}\ |\ a \equiv 0\text{ (mod 3)}\},} \\ {C[1]} &= & {\{a \in \mathbb{Z}\ |\ a \equiv 1\text{ (mod 3)}\},\text{ and}} \\ {C[2]} &= & {\{a \in \mathbb{Z}\ |\ a \equiv 2\text{ (mod 3)}\}.} \end{array}\]

Los principales resultados que queremos usar ahora son el Teorema 3.31 y el Corolario 3.32 en la página 150. Este corolario nos dice que para cualquiera\(a \in \mathbb{Z}\),\(a\) es congruente precisamente con uno de los enteros 0, 1 o 2. En consecuencia, el entero\(a\) debe ser congruente con 0, 1 o 2, y no puede ser congruente con dos de estos números. Así

1. Para cada uno\(a \in \mathbb{Z}\)\(a \in C[0]\),,\(a \in C[1]\), o\(a \in C[2]\); y
2. \(C[0] \cap C[1] = \emptyset\),\(C[0] \cap C[2] = \emptyset\), y\(C[1] \cap C[2] = \emptyset\).

Esto significa que la relación de congruencia módulo 3 ordena los enteros en tres conjuntos distintos, o clases, y que cada par de estos conjuntos no tiene elementos en común. Entonces, si usamos un rectángulo para representar\(\mathbb{Z}\), podemos dividir ese rectángulo en tres rectángulos más pequeños, correspondientes a\(C[0]\)\(C[1]\), y\(C[2]\) y podríamos imaginarnos esta situación de la siguiente manera:

Los enteros

\(C[0]\)que consiste en todos los números enteros con un resto de 0 cuando se divide por 3

\(C[1]\)que consiste en todos los números enteros con un resto de 1 cuando se divide por 3

\(C[2]\)que consiste en todos los números enteros con un resto de 2 cuando se divide por 3

Cada entero está exactamente en uno de los tres conjuntos (C [0]\)\(C[1]\), o\(C[2]\), y dos enteros son congruentes módulo 3 si y sólo si están en el mismo conjunto. Veremos que, de manera similar, si\(n\) hay algún número natural, entonces la relación de módulo de congruencia se\(n\) puede utilizar para ordenar los enteros en\(n\) clases. También veremos que en general, si tenemos una relación de equivalencia\(R\) en un conjunto\(A\), podemos ordenar los elementos del conjunto\(A\) en clases de manera similar.

Definición

Dejar\(\sim\) ser una relación de equivalencia sobre un conjunto no vacío\(A\). Para cada uno\(a \in A\), la clase de equivalencia de\(a\) determinada por\(\sim\) es el subconjunto de\(A\), denotado por [\(a\)], que consiste en todos los elementos de los\(A\) que son equivalentes a\(a\). Es decir,

\([a] = \{x \in A\ |\ x \sim a\}.\)

Leemos [\(a\)] como “la clase de equivalencia de\(a\)" o como “corchete”\(a\).

Notas

1. Usamos la notación [\(a\)] cuando solo se está utilizando una relación de equivalencia. Si hay más de una relación de equivalencia, entonces necesitamos distinguir entre las clases de equivalencia para cada relación. A menudo usamos algo así como\([a]_{\sim}\), o si\(R\) es el nombre de la relación, podemos usar\(R[a]\) o\([a]_R\) para la clase de equivalencia de un determinado por\(R\). En cualquier caso, recuerde siempre que cuando estamos trabajando con alguna relación de equivalencia en un conjunto A si\(a \in A\), entonces la clase de equivalencia [\(a\)] es un subconjunto de\(A\).
2. Sabemos que cada entero tiene una clase de equivalencia para la relación de equivalencia de congruencia módulo 3. Pero como hemos visto, en realidad sólo hay tres clases de equivalencia distintas. Usando la notación de la definición, son:
   
   \([0] = \{a \in \mathbb{Z}\ |\ a \equiv 0 \text{ (mod 3)}\},\)
   \([1] = \{a \in \mathbb{Z}\ |\ a \equiv 1 \text{ (mod 3)}\},\) y
   \([2] = \{a \in \mathbb{Z}\ |\ a \equiv 2 \text{ (mod 3)}\}.\)

Comprobación de progreso 7.12 (Clases de equivalencia de la actividad previa\(\PageIndex{1}\))

Sin usar la terminología en ese momento, en realidad determinamos las clases de equivalencia de la relación de equivalencia\(R\) en Actividad Previa\(\PageIndex{1}\). ¿Cuáles son las distintas clases de equivalencia para esta relación de equivalencia?

Responder

Agrega textos aquí. No elimine primero este texto.

Congruencia Modulo\(n\) y Clases de Congruencia

En Preview Activity\(\PageIndex{2}\), usamos la notación\(C[k]\) para el conjunto de todos los enteros que son congruentes con el\(k\) módulo 3. Podríamos haber utilizado una notación similar para las clases de equivalencia, y esto hubiera sido perfectamente aceptable. Sin embargo, la notación [\(a\)] es probablemente la notación más común para la clase de equivalencia de\(a\). Ahora usaremos esta misma notación al tratar con módulo de congruencia\(n\) cuando solo se esté considerando una relación de congruencia.

Definición: clase de congruencia de\(a\) modulo \(n\).

Vamos\(n \in \mathbb{N}\). El módulo de congruencia\(n\) es una relación de equivalencia sobre\(\mathbb{Z}\). Así que para\(a \in \mathbb{Z}\),

\([a] = \{x \in \mathbb{Z}\ |\ x \equiv a \text{ (mod \(n\))}\}.\)

En este caso, [\(a\)] se llama la clase de congruencia de\(a\) módulo\(n\).

Hemos visto que congruencia módulo 3 divide los enteros en tres clases de congruencia distintas. Cada clase de congruencia consiste en aquellos enteros con el mismo resto cuando se divide por 3. De manera similar, si usamos congruencia módulo 2, simplemente dividimos los enteros en dos clases. Una clase constará de todos los enteros que tienen un resto de 0 cuando se divide por 2, y la otra clase consistirá en todos los enteros que tienen un resto de 1 cuando se dividen por 2. Es decir, congruencia módulo 2 simplemente divide los enteros en los enteros pares e impares.

Comprobación de Progreso 7.13: Congruencia Modulo 4

Determinar todas las clases de congruencia distintas para la relación de equivalencia del módulo 4 de congruencia en los enteros. Especifique cada clase de congruencia usando el método roster.

Responder

Agrega textos aquí. No elimine primero este texto.

Propiedades de Clases de Equivalencia

Como hemos visto, en Preview Activity\(\PageIndex{1}\), la relación R fue una relación de equivalencia. Para esa actividad de vista previa, usamos\(R[y]\) para denotar la clase de equivalencia de\(y \in A\), y observamos que estas clases de equivalencia eran iguales o disjuntas.

Sin embargo, en Preview Activity\(\PageIndex{1}\), la relación no\(S\) era una relación de equivalencia, y por lo tanto no utilizamos el término “clase de equivalencia” para esta relación. Debemos señalar, sin embargo, que los conjuntos no\(S[y]\) fueron iguales y no fueron disjuntos. Esto exhibe una de las principales distinciones entre las relaciones de equivalencia y las relaciones que no son relaciones de equivalencia.

En el Teorema 7.14, vamos a demostrar que si\(\sim\) es una relación de equivalencia en el conjunto\(A\), entonces podemos “ordenar” los elementos de\(A\) en distintas clases de equivalencia. Las propiedades de las clases de equivalencia que probaremos son las siguientes: (1) Cada elemento de A está en su propia clase de equivalencia; (2) dos elementos son equivalentes si y sólo si sus clases de equivalencia son iguales; y (3) dos clases de equivalencia son idénticas o son disjuntas.

Teorema 7.14

Dejar\(A\) ser un conjunto no vacío y dejar\(\sim\) ser una relación de equivalencia en el conjunto\(A\). Entonces,

1. Para cada uno\(a \in A\),\(a \in [a]\).
2. Para cada uno\(a, b \in A\),\(a \sim b\) si y sólo si\([a] = [b]\),
3. Para cada uno\(a, b \in A\),\([a] = [b]\) o\([a] \cap [b] = \emptyset\).

Prueba

Que A sea un conjunto no vacío y supongamos que\(\sim\) es una relación de equivalencia en\(A\). Para probar la primera parte del teorema, vamos\(a \in A\). Ya que\(\sim\) es una relación de equivalencia sobre\(A\), es reflexiva sobre\(A\). Así,\(a \sim a\), y podemos concluir que\(a \in [a]\).

La segunda parte de este teorema es una declaración bicondicional. Lo probaremos probando dos declaraciones condicionales. Primero lo probaremos si\(a \sim b\), entonces\([a] = [b]\). Así que vamos\(a, b \in A\) y asumamos eso\(a \sim b\). Ahora vamos a demostrar que los dos conjuntos\([a]\) y\([b]\) son iguales. Esto lo haremos demostrando que cada uno es un subconjunto del otro.

Primero, asuma eso\(x \in [a]\). Entonces, por definición,\(x \sim a\). Ya que hemos asumido eso\(a \sim b\), podemos usar la propiedad transitiva de\(\sim\) para concluir eso\(x \sim b\), y esto significa que\(x \in [b]\). Esto lo demuestra\([a] \subseteq [b]\).

Ahora asumimos eso\(y \in [b]\). Esto significa que\(y \sim b\), y por lo tanto por la propiedad simétrica, eso\(b \sim y\). Nuevamente, estamos asumiendo eso\(a \sim b\). Así que tenemos

\(a \sim b\)y\(b \sim y\).

Usamos la propiedad transitiva para concluir eso\(a \sim y\) y luego, usando la propiedad simétrica, concluimos que\(y \sim a\). Esto prueba eso\(y \in [a]\) y, por lo tanto, eso\([b] \subseteq [a]\). Esto significa que podemos concluir que si\(a \sim b\), entonces\([a] = [b]\).

Ahora debemos probarlo si\([a] = [b]\), entonces\(a \sim b\). Dejemos\(a, b \in A\) y asumamos eso\([a] = [b]\). Usando la primera parte del teorema, lo sabemos\(a \in [a]\) y como los dos conjuntos son iguales, esto nos dice eso\(a \in [b]\). De ahí que por la definición de\([b]\), concluimos que\(a \sim b\). Esto completa la prueba de la segunda parte del teorema.

Para la tercera parte del teorema, vamos\(a, b \in A\). Dado que esta parte del teorema es una disyunción, consideraremos dos casos: O bien

\([a] \cap [b] = \emptyset\)o\([a] \cap [b] \ne \emptyset\).

En el caso donde\([a] \cap [b] = \emptyset\), la primera parte de la disyunción es cierta, y de ahí no hay nada que probar. Entonces asumimos eso\([a] \cap [b] \ne \emptyset\); y lo demostraremos\([a] = [b]\). Ya que\([a] \cap [b] \ne \emptyset\), hay un elemento\(x\) en\(A\) tal que

\(a \in [a] \cap [b]\).

Esto significa que\(x \in [a]\) y\(x \in [b]\). En consecuencia\(x \in b\),\(x \in a\) y, y así podemos utilizar la primera parte del teorema para concluir que\([x] = [a]\) y\([x] = [b]\). De ahí\([a] = [b]\),, y hemos demostrado que\([a] = [b]\) o\([a] \cap [b] = \emptyset\).

El teorema 7.14 da las propiedades primarias de las clases de equivalencia. Las consecuencias de estas propiedades serán exploradas en los ejercicios. En la siguiente tabla se reafirman las propiedades en el Teorema 7.14 y se da una descripción verbal de cada una.

Declaración Formal del Teorema 7.14	Descripción Verbal
Para cada uno\(a \in A\),\(a \in [a]\).	Cada elemento de\(A\) está en su propia clase de equivalencia.
Para cada uno\(a, b \in A\),\(a \sim b\) si y solo si\([a] = [b]\).	Dos elementos de\(A\) son equivalentes si y sólo si sus clases de equivalencia son iguales.
Para cada uno\(a, b \in A\),\([a] = [b]\) o\([a] \cap [b] = \emptyset\)	Cualquiera de las dos clases de equivalencia son iguales o disjuntas. Esto quiere decir que si dos clases de equivalencia no son disjuntas entonces deben ser iguales.

Comprobación de Progreso 7.15: Clases de Equivalencia

Dejar\(f: \mathbb{R} \to \mathbb{R}\) ser definido por\(f(x) = x^2 - 4\) para cada uno\(x \in \mathbb{R}\). Defina una relación\(\sim\) de la\(\mathbb{R}\) siguiente manera:

Para\(a, b \in \mathbb{R}\),\(a \sim b\) si y solo si\(f(a) = f(b)\).

En el Ejercicio (6) de la Sección 7.2, probamos que\(\sim\) es una relación de equivalencia sobre\(\mathbb{R}\). En consecuencia, cada número real tiene una clase de equivalencia. Para esta relación de equivalencia,

1. Determinar las clases de equivalencia de 5, -5, 10, -10\(\pi\), y\(-\pi\).
2. Determinar la clase de equivalencia de 0.
3. Si\(a \in \mathbb{R}\), utilice el método roster para especificar los elementos de la clase de equivalencia\([a]\).

Responder

Agrega textos aquí. No elimine primero este texto.

Los resultados del Teorema 7.14 son consistentes con todas las relaciones de equivalencia estudiadas en las actividades de vista previa y en las comprobaciones de progreso. Dado que este teorema se aplica a todas las relaciones de equivalencia, se aplica a la relación de módulo de congruencia\(n\) sobre los enteros. Debido a la importancia de esta relación de equivalencia, estos resultados para congruencia módulo n se dan en el siguiente corolario.

Corolario 7.16.

Vamos\(n \in \mathbb{N}\). Para cada uno\(a \in \mathbb{Z}\), vamos a\([a]\) representar la clase de congruencia de\(a\) módulo\(n\).

1. Para cada uno\(a \in \mathbb{Z}\),\(a \in [a]\).
2. Para cada uno\(a, b \in \mathbb{Z}\),\(a \equiv b\) (mod\(n\)) si y solo si\([a] = [b]\).
3. Para cada uno\(a, b \in \mathbb{Z}\),\([a] = [b]\) o\([a] \cap [b] = \emptyset\).

Para la relación de equivalencia del módulo de congruencia\(n\), el Teorema 3.31 y el Corolario 3.32 nos dicen que cada entero es congruente con su resto cuando se divide por\(n\), y que cada entero es módulo\(n\) congruente con precisamente uno de los enteros\(0, 1, 2, ..., n - 1\). Esto significa que cada entero está precisamente en una de las clases de congruencia\([0], [1], [2], ..., [n - 1]\). De ahí que el Corolario 7.16 nos da el siguiente resultado

Teorema\(\PageIndex{1}\)

Vamos\(n \in \mathbb{N}\). Para cada uno\(a \in \mathbb{Z}\), vamos a\([a]\) representar la clase de congruencia de\(a\) módulo\(n\).

1. \(\mathbb{Z} = [0] \cup [1] \cup [2] \cup \cdot\cdot\cdot \cup [n - 1]\)
2. Para\(j, k \in \{0, 1, 2, ..., n -1\}\), si\(j \ne k\), entonces\([j] \cap [k] = \emptyset\).

Particiones y Relaciones de Equivalencia

Una partición de un conjunto\(A\) es una colección de subconjuntos\(A\) que “divide” el conjunto\(A\) en subconjuntos disjuntos. Técnicamente, cada par de subconjuntos distintos de la colección debe ser disjunta. Entonces decimos que la colección de subconjuntos es disjunta por pares. Introducimos la siguiente definición formal.

Definición: partición de\(A\)

Dejar\(A\) ser un conjunto no vacío, y dejar\(\mathcal{C}\) ser una colección de subconjuntos de\(A\). La colección de subconjuntos\(\mathcal{C}\) es una partición de\(A\) siempre que

1. Para cada uno\(V \in \mathcal{C}\),\(V \ne \emptyset\).
2. Para cada uno\(x \in A\), existe\(V \in \mathcal{C}\) tal que\(x \in V\).
3. Para cada\(V, W \in \mathcal{C}\),\(V = W\) o\(V \cap W = \emptyset\).

Existe una estrecha relación entre particiones y clases de equivalencia ya que las clases de equivalencia de una relación de equivalencia forman una partición del conjunto subyacente, como se demostrará en el Teorema 7.18. La prueba de este teorema se basa en los resultados del Teorema 7.14.

Teorema 7.18

Dejar\(\sim\) ser una relación de equivalencia sobre el conjunto no vacío\(A\). Entonces la colección\(\mathcal{C}\) de todas las clases de equivalencia determinadas por\(\sim\) es una partición del conjunto\(A\).

Prueba

Dejar\(\sim\) ser una relación de equivalencia sobre el conjunto no vacío\(A\), y dejar\(\mathcal{C}\) ser la colección de todas las clases de equivalencia determinadas por\(\sim\). Es decir,

\(\mathcal{C} = \{[a]\ |\ a \in A\}\).

Vamos a utilizar el Teorema 7.14 para demostrar que\(\mathcal{C}\) es una partición de\(A\).

La Parte (1) del Teorema 7.14 establece que para cada uno\(a \in A\),\(a \in [a]\). En términos de las clases de equivalencia, esto significa que cada clase de equivalencia no está vacía ya que cada elemento de\(A\) está en su propia clase de equivalencia. En consecuencia\(\mathcal{C}\),, la colección de todas las clases de equivalencia determinadas por\(\sim\), satisface las dos primeras condiciones de la definición de una partición.

Ahora debemos demostrar que la colección\(\mathcal{C}\) de todas las clases de equivalencia determinadas por\(\sim\) satisface la tercera condición para ser una partición. Es decir, necesitamos demostrar que dos clases de equivalencia cualesquiera son iguales o disjuntas. Sin embargo, este es exactamente el resultado en la Parte (3) del Teorema 7.14.

De ahí que se haya comprobado que la colección C de todas las clases de equivalencia determinadas por\(\sim\) es una partición del conjunto A.

Nota: El teorema 7.18 nos ha demostrado que si\(\sim\) es una relación de equivalencia sobre un conjunto no vacío\(A\), entonces la colección de las clases de equivalencia determinadas por\(\sim\) formar una partición del conjunto\(A\).

Este proceso se puede revertir. Esto significa que dada una partición\(\mathcal{C}\) de un conjunto no vacío\(A\), podemos definir una relación de equivalencia en\(A\) cuyas clases de equivalencia son precisamente los subconjuntos de\(A\) que forman la partición. Esto se explorará en Ejercicio (12).

Ejercicio 7.3

1. Dejar\(A = \{a, b, c, d, e\}\) y dejar\(\sim\) ser la relación sobre la\(A\) que está representada por la gráfica dirigida en la Figura 7.4.
   
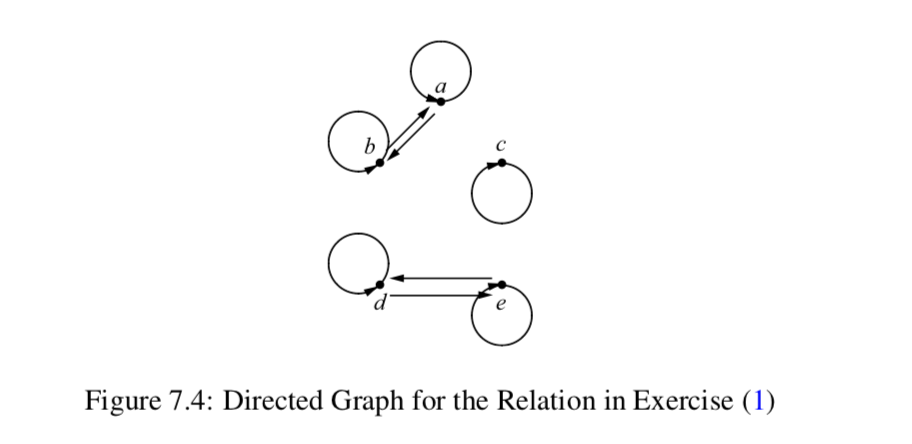
   Demostrar que\(\sim\) es una relación de equivalencia en el conjunto\(A\), y determinar todas las clases de equivalencia determinadas por esta relación de equivalencia.
2. Vamos\(A = \{a, b, c, d, e, f\}\), y supongamos que\(\sim\) es una relación de equivalencia sobre\(A\). También supongamos que se sabe que
   \(a \sim b\)\(a \nsim c\)\(e \sim f\)
   \(a \sim d\)\(a \nsim f\)\(e \nsim c\)
   Dibuja una gráfica dirigida completa para la relación de equivalencia\(\sim\) en el conjunto\(A\), y luego determinar todas las clases de equivalencia para esta relación de equivalencia.
3. Vamos\(A = \{0, 1, 2, 3, ..., 999, 1000\}\). Definir\(R\) la relación\(A\) como sigue:
   Para\(x, y \in A\),\(x\ R\ y\) si y solo si\(x\) y\(y\) tener el mismo número de dígitos.

   Demostrar que\(R\) es una relación de equivalencia en el conjunto\(A\) y determinar todas las clases de equivalencia distintas determinadas por\(R\).

4. Determinar todas las clases de congruencia para la relación de congruencia módulo 5 en el conjunto de enteros.
5. Vamos\(\mathbb{Z}_9 = \{0, 1, 2, 3, 4, 5, 6, 7, 8\}\).
   a) Definir la relación de\(\sim\) la\(\mathbb{Z}_9\) siguiente manera: para todos\(a, b \in \mathbb{Z}_9\),\(a \sim b\) si y sólo si\(a^2 \equiv b^2\) (mod 9). Demostrar que\(\sim\) es una relación de equivalencia\(\mathbb{Z}_9\) y determinar todas las clases de equivalencia distintas de esta relación de equivalencia.
   b) Definir la relación de\(\approx\) la\(\mathbb{Z}_9\) siguiente manera: Para todos\(a, b \in \mathbb{Z}_9\),\(a \approx b\) si y sólo si\(a^3 \equiv b^3\) (mod 9). Demostrar que\(\approx\) es una relación de equivalencia\(\mathbb{Z}_9\) y determinar todas las clases de equivalencia distintas de esta relación de equivalencia.
6. Defina la relación\(\sim\) de la\(\mathbb{Q}\) siguiente manera: Para\(a, b \in \mathbb{Q}\),\(a \sim b\) si y solo si\(a - b \in \mathbb{Z}\). En Avance Comprobación 7.9 de la Sección 7.2, se demostró que la relación\(\sim\) es una relación de equivalencia sobre\(\mathbb{Q}\). También, véase Ejercicio (9) en la Sección 7.2.
   
   a) Demostrarlo\([\dfrac{5}{7} = \{m + \dfrac{5}{7}\ |\ m \in \mathbb{Z}\}\).
   b) Si\(a \in \mathbb{Z}\), entonces, ¿cuál es la clase de equivalencia\(a\)?
   (c) Si\(a \in \mathbb{Z}\), demostrar que existe una biyección de\([a]\) a\([\dfrac{5}{7}]\).
7. Defina la relación\(\sim\) de la\(\mathbb{R}\) siguiente manera:
   Para\(x, y \in \mathbb{R}\),\(x \sim y\) si y solo si\(x - y \in \mathbb{Q}\).
   
   a) Demostrar que\(\sim\) es una relación de equivalencia sobre\(\mathbb{R}\).
   b) Enumerar cuatro números reales diferentes que se encuentran en la clase de equivalencia de\(\sqrt{2}\).
   c) Si\(a \in \mathbb{Q}\), ¿cuál es la clase de equivalencia\(a\)?
   d) Demostrarlo\([\sqrt{2}] = \{r + \sqrt{2}\ |\ r \in \mathbb{Q}\}\).
   (e) Si\(a \in \mathbb{Q}\), demostrar que existe una biyección de\([a]\) a\([\sqrt{2}]\).
8. Define la relación\(\sim\) sobre de la\(\mathbb{Z}\) siguiente manera: Para\(a, b \in \mathbb{Z}\),\(a \sim b\) si y solo si\((2a + 3b \equiv 0\) (mod 5). La relación\(\sim\) es una relación de equivalencia sobre\(\mathbb{Z}\). (Ver Ejercicio (13) en la Sección 7.2). Determinar todas las clases de equivalencia distintas para esta relación de equivalencia.
9. Vamos\(A = \mathbb{Z} \times (\mathbb{Z} - \{0\})\). Es decir,\(A = \{(a, b) \in \mathbb{Z} \times \mathbb{Z}\ |\ b \ne 0\}\). Defina la relación\(\approx\) de la\(A\) siguiente manera:
   Para\((a, b), (c, d) \in A\),\((a, b) \approx (c, d)\) si y solo si\(ad = bc\).
   
   a) Demostrar que\(\approx\) es una relación de equivalencia sobre\(A\).
   b) ¿Por qué fue necesario incluir la restricción que\(b \ne 0\) en la definición del conjunto\(A\)?
   (c) Determinar una ecuación que dé una relación entre\(a\) y\(b\) si\((a, b) \in A\) y\((a, b) \approx (2, 3)\).
   d) Determinar al menos cuatro elementos diferentes en [(2, 3)], la clase de equivalencia de (2, 3).
   (e) Utilice la noción de constructor de conjuntos para describir [(2, 3)], la clase de equivalencia de (2, 3).
10. Para\((a, b) (c, d) \in \mathbb{R} \times \mathbb{R}\), defina\((a, b) \sim (c, d)\) si y solo si\(a^2 + b^2 = c^2 + d^2\). En el Ejercicio (15) de la Sección 7.2, probamos que\(\sim\) es una relación de equivalencia sobre\(\mathbb{R} \times \mathbb{R}\).
    
    (a) Determinar la clase de equivalencia de (0, 0).
    (b) Utilice la notación set builder (y no utilice el símbolo\(\sim\)) para describir la clase de equivalencia de (2, 3) y luego dar una descripción geométrica de esta clase de equivalencia.
    c) Dar una descripción geométrica de una clase de equivalencia típica para esta relación de equivalencia.
    (d) Dejar\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\). Demostrar que existe una correspondencia uno a uno (biyección) entre\(\mathbb{R}^{\ast}\) y el conjunto de todas las clases de equivalencia para esta relación de equivalencia.
11. Dejar\(A\) ser un conjunto no vacío y dejar\(\sim\) ser una relación de equivalencia en\(A\). Demostrar cada uno de los siguientes: a
    
    ) Para cada uno\(a, b \in A\),\(a \nsim b\) si y sólo si\([a] \cap [b] = \emptyset\).
    b) Para cada uno\(a, b \in A\), si\([a] \ne [b]\), entonces\([a] \cap [b] = \emptyset\).
    (c) Para cada uno\(a, b \in A\), si\([a] \cap [b] \ne \emptyset\) entonces\([a] = [b]\).
    
    Exploraciones y actividades
12. Una partición define una relación de equivalencia. Dejar\(A = \{a, b, c, d, e\}\) y dejar\(\mathcal{C} = \{\{a, b, c\}, \{d, e\}\}\).
    
    (a) Explicar por qué\(\mathcal{C}\) es una partición de\(A\).
    
    Definir una relación\(\sim\) sobre de la\(A\) siguiente manera: Para\(x, y \in A\),\(x \sim y\) si y sólo si existe un conjunto\(U\) en\(\mathcal{C}\) tal que\(x \in U\) y\(y \in U\).
    
    b) Demostrar que\(\sim\) es una relación de equivalencia en el conjunto\(A\), y luego determinar todas las clases de equivalencia para\(\sim\). ¿Cómo se compara la colección de todas las clases de equivalencia\(\mathcal{C}\)?
    
    Lo que hicimos para la partición específica en la Parte (12b) se puede hacer para cualquier partición de un conjunto. Entonces para generalizar la Parte (12b), dejamos\(A\) ser un conjunto no vacío y dejamos\(\mathcal{C}\) ser una partición de\(A\). Luego definimos una relación\(\sim\) sobre de la\(A\) siguiente manera:
    Para\(x, y \in A\),\(x \sim y\) si y sólo si existe un conjunto\(U\) en\(\mathcal{C}\) tal que\(x \in U\) y\(y \in U\).
    
    c) Demostrar que\(\sim\) es una relación de equivalencia en el conjunto\(A\).
    d) Dejar\(a \in A\) y dejar\(U \in \mathcal{C}\) tal que\(a \in U\). \([a] = U\)Demuéstralo.
13. Relaciones de equivalencia en un conjunto de matrices. Los siguientes ejercicios requieren un conocimiento de álgebra lineal elemental. Dejamos\(\mathcal{M}_{n,n} (\mathbb{R}\) ser el conjunto de todas\(n\) por\(n\) matrices con entradas de número real.
    
    a) Definir una relación\(\sim\) sobre de la\(\mathcal{M}_{n,n} (\mathbb{R}\) siguiente manera: Para todos\(A, B \in \mathcal{M}_{n,n} (\mathbb{R}\),\(A \sim B\) si y sólo si existe una matriz invertible\(P\) en\(\mathcal{M}_{n,n} (\mathbb{R}\) tal que\(B = PAP^{-1}\). ¿Está\(\sim\) encendida una relación de equivalencia\(\mathcal{M}_{n,n} (\mathbb{R}\)? Justifica tu conclusión.
    b) Definir una relación de\(R\) la\(\mathcal{M}_{n,n} (\mathbb{R}\) siguiente manera: Para todos\(A, B \in \mathcal{M}_{n,n} (\mathbb{R}\),\(A\ R\ B\) si y sólo si det (\(A\)) = det (\(B\)). ¿Está\(R\) encendida una relación de equivalencia\(\mathcal{M}_{n,n} (\mathbb{R}\)? Justifica tu conclusión.
    (c)\(\sim\) Sea una relación de equivalencia sobre\(\mathbb{R}\). Definir una relación\(\approx\) de la\(\mathcal{M}_{n,n} (\mathbb{R}\) siguiente manera: Para todos\(A, B \in \mathcal{M}_{n,n} (\mathbb{R}\),\(A \approx B\) si y solo si det (\(A\))\(\sim\) det (\(B\)). ¿Está\(\approx\) encendida una relación de equivalencia\(\mathcal{M}_{n,n} (\mathbb{R}\)? Justifica tu conclusión.

Responder

Agrega textos aquí. No elimine primero este texto.