7.4: Aritmética Modular

PREVIAR ACTIVIDAD\(\PageIndex{1}\): Congruence Modulo 6

Para esta actividad de vista previa, solo usaremos la relación de congruencia módulo 6 en el conjunto de enteros.

1. Encuentra cinco enteros diferentes a tal que\(a \equiv 3\) (mod 6) y encuentra cinco enteros diferentes\(b\) tal que\(b \equiv 4\) (mod 6). Es decir, encontrar cinco enteros diferentes en [3], la clase de congruencia de 3 módulo 6 y cinco enteros diferentes en [4], la clase de congruencia de 4 módulo 6.
2. Calcular\(s = a + b\) usando varios valores de\(a\) en [3] y varios valores de\(b\) en [4] de la Parte (1). Por cada suma\(s\) que se calcula, encuentra\(r\) así que\(0 \le r < 6\) y\(s \equiv r\) (mod 6). ¿Qué observas?
3. Calcular\(p = a \cdot b\) usando varios valores de\(a\) en [3] y varios valores de\(b\) en [4] de la Parte (1). Por cada producto\(p\) que se calcula, encuentra\(r\) así que eso\(0 \le r < 6\) y\(p \equiv r\) (mod 6). ¿Qué observas?
4. Calcular\(q = a^2\) usando varios valores de a en [3] de la Parte (1). Por cada producto\(q\) que se calcula, encuentra\(r\) así que eso\(0 \le r < 6\) y\(q \equiv r\) (mod 6). ¿Qué observas?

PREVIAR ACTIVIDAD\(\PageIndex{2}\): The Remainder When Dividing by 9

Si a y b son enteros con b > 0, entonces desde el Algoritmo de División, sabemos que existen enteros únicos\(q\) y\(r\) tales que

\(a =bq + r\)y\(0 \le r < b\).

En esta actividad, nos interesa el resto\(r\). Observe eso\(r = a - bq\). Entonces, dado\(a\) y\(b\), si podemos calcular\(q\), entonces podemos calcular\(r\).

Podemos usar la función “int” en una calculadora para calcular\(q\). [La función “int” es la “mayor función entera”. Si\(x\) es un número real, entonces int (\(x\)) es el mayor número entero que es menor o igual a\(x\).]

Entonces, en el contexto del Algoritmo de División,\(q = \text{int}(\dfrac{a}{b})\). En consecuencia,

\(r = a - b \cdot \text{int}(\dfrac{a}{b})\).

Si\(n\) es un entero positivo, vamos a dejar\(s(n)\) denotar la suma de los dígitos de\(n\). Por ejemplo, si\(n = 731\), entonces

\(s(731) = 7 + 3 + 1 = 11\).

Para cada uno de los siguientes valores de\(n\), calcular

• El resto cuando\(n\) se divide por 9, y
• El valor de\(s(n)\) y el resto cuando\(s(n)\) se divide por 9.

1. \(n = 498\)
2. \(n = 7319\)
3. \(n = 4672\)
4. \(n = 9845\)
5. \(n = 51381\)
6. \(n = 305877\)

¿Qué observas?

El módulo de enteros\(n\)

Vamos\(n \in \mathbb{N}\). Dado que la relación de congruencia módulo n es una relación de equivalencia sobre\(\mathbb{Z}\), podemos discutir sus clases de equivalencia. Recordemos que en esta situación, nos referimos a las clases de equivalencia como clases de congruencia.

Definición: integers modulo\(n\)

Vamos\(n \in \mathbb{N}\). El conjunto de clases de congruencia para la relación de congruencia módulo\(n\) on\(\mathbb{Z}\) es el conjunto de enteros módulo\(n\), o el conjunto de enteros mod\(n\). Denotaremos este conjunto de clases de congruencia por\(\mathbb{Z}_n\).

Corolario 7.17 nos dice que

\(\mathbb{Z} = [0] \cup [1] \cup [2] \cup \cdot\cdot\cdot \cup [n - 1]\).

Además, sabemos que cada entero es congruente con precisamente uno de los enteros 0, 1, 2,...,\(n - 1\). Esto nos dice que una forma de representar\(\mathbb{Z}_n\) es

\(\mathbb{Z}_n = \{[0], [1], [2], ... [n - 1]\}\).

En consecuencia, aunque cada entero tiene una clase de congruencia, el conjunto solo\(\mathbb{Z}_n\) tiene clases de congruencia\(n\) distintas.

El conjunto de enteros\(\mathbb{Z}\) es más que un conjunto. Podemos sumar y multiplicar enteros. Es decir, están las operaciones aritméticas de suma y multiplicación en el conjunto\(\mathbb{Z}\), y sabemos que\(\mathbb{Z}\) se cierra con respecto a estas dos operaciones.

Uno de los problemas básicos tratados en el álgebra moderna es determinar si las operaciones aritméticas en un conjunto “se transfieren” a un conjunto relacionado. En este caso, el conjunto relacionado es\(\mathbb{Z}_n\). Por ejemplo, en los enteros módulo 5,\(\mathbb{Z}_5\), ¿es posible agregar las clases de congruencia [4] y [2] de la siguiente manera?

\[\begin{array} {rcl} {[4] \oplus [2]} &= & {[4 + 2]} \\ {} &= & {[6]} \\ {} &= & {[1].} \end{array}\]

Hemos utilizado el símbolo para denotar adición en\(\mathbb{Z}_5\) para que no lo confundamos con adición en\(\mathbb{Z}\). Esto parece bastante simple, pero hay un problema. Las clases de congruencia [4] y [2] no son números, son conjuntos infinitos. Tenemos que asegurarnos de que obtenemos la misma respuesta sin importar qué elemento de [4] usemos y no importa qué elemento de [2] usamos. Por ejemplo,

\(9 \equiv 4\)(mod 5) y así [9] = [4]. También,
\(7 \equiv 2\) (mod 5) y así [7] = [2].

¿Obtenemos el mismo resultado si sumamos [9] y [7] de la manera en que lo hicimos cuando agregamos [4] y [2]? El siguiente cálculo confirma que hacemos:

\[\begin{array} {rcl} {[9] \oplus [7]} &= & {[9 + 7]} \\ {} &= & {[16]} \\ {} &= & {[1].} \end{array}\]

Esta es una de las ideas que se exploró en Preview Activity\(\PageIndex{1}\). La principal diferencia es que en esta actividad de vista previa, utilizamos la relación de congruencia, y aquí estamos usando clases de congruencia. Todos los ejemplos en Preview Activity\(\PageIndex{1}\) deberían haber ilustrado las propiedades del módulo de congruencia 6 en la siguiente tabla. El lado izquierdo muestra las propiedades en términos de la relación de congruencia y el lado derecho muestra las propiedades en términos de las clases de congruencia.

Si\(a \equiv 3\) (mod 6) y\(b \equiv 4\) (mod 6), entonces \((a + b) \equiv (3 + 4)\)(mod 6); \((a \cdot b) \equiv (3 \cdot 4)\)(mod 6).

Si\([a] = [3]\) y\([b] = [4]\) dentro\(\mathbb{Z}_6\), entonces \([a + b] = [3 + 4]\); \([a \cdot b] = [3 \cdot 4]\).

Estas son ilustraciones de propiedades generales que ya hemos probado en el Teorema 3.28. Repetimos aquí la afirmación del teorema porque es muy importante para definir las operaciones de suma y multiplicación en\(\mathbb{Z}_n\).

Teorema 3.28

Dejar\(n\) ser un número natural y dejar\(a\)\(b\),\(c\),, y\(d\) ser enteros. Entonces

1. Si\(a \equiv b\) (mod\(n\)) y\(c \equiv d\) (mod\(n\)), entonces\((a + c) \equiv (b + d)\) (mod\(n\)).
2. Si\(a \equiv b\) (mod\(n\)) y\(c \equiv d\) (mod\(n\)), entonces\(ac \equiv bd\) (mod\(n\)).
3. Si\(a \equiv b\) (mod\(n\)) y\(m \in \mathbb{N}\), entonces\(a^m \equiv b^m\) (mod\(n\)).

Prueba

Agrega prueba aquí y automáticamente se ocultará

Desde\(x \equiv y\) (mod\(n\)) si y solo si\([x] = [y]\), podemos reafirmar el resultado de este Teorema 3.28 en cuanto a clases de congruencia en\(\mathbb{Z}_n\).

Corolario 7.19.

Dejar\(n\) ser un número natural y dejar\(a\)\(b\),\(c\),, y\(d\) ser enteros. Entonces, en\(\mathbb{Z}_n\).

1. Si\([a] = [b]\) y\([c] = [d]\), entonces\([a + c] = [b + d]\).
2. Si\([a] = [b]\) y\([c] = [d]\), entonces\([a \cdot c] = [b \cdot d]\).
3. Si\([a] = [b]\) y\(m \in \mathbb{N}\), entonces\([a]^m = [b]^m\).

Debido al Corolario 7.19, sabemos que la siguiente definición formal de adición y multiplicación de clases de congruencia en\(\mathbb{Z}_n\) es independiente de la elección de los elementos que elegimos de cada clase. Decimos que estas definiciones de suma y multiplicación están bien definidas.

Definición

Vamos\(n \in \mathbb{N}\). La suma y multiplicación en\(\mathbb{Z}_n\) se definen de la siguiente manera: Para\([a], [c] \in \mathbb{Z}_n\),

\([a] \oplus [c] = [a + c]\)y\([a] \odot [c] = [ac]\).

El término aritmética modular se utiliza para referirse a las operaciones de suma y multiplicación de clases de congruencia en el módulo de enteros\(n\).

Entonces si\(n \in \mathbb{N}\), entonces tenemos una suma y multiplicación definida en\(\mathbb{Z}_n\), los enteros módulo\(n\).

Recuerde siempre que para cada una de las ecuaciones en las definiciones, las operaciones de la izquierda,\(\oplus\) y\(\odot\), son las nuevas operaciones que se están definiendo. Las operaciones en el lado derecho de las ecuaciones (+ y\(\cdot\)) son las operaciones conocidas de suma y multiplicación en\(\mathbb{Z}\).

Dado que\(\mathbb{Z}_n\) es un conjunto finito, es posible construir tablas de suma y multiplicación para\(\mathbb{Z}_n\). Al construir estas tablas, seguimos la convención de que todas las sumas y productos deben estar en la forma [\(r\)], donde\(0 \le r < n\). Por ejemplo, en\(\mathbb{Z}_3\), vemos eso por la definición,\([1] \oplus [2] = [3]\), pero desde\(3 \equiv 0\) (mod 3), vemos eso\([3] = [0]\) y así escribimos

\([1] \oplus [2] = [3] = [0]\)

Del mismo modo, por definición\([2] \odot [2] = [4]\), y en\(\mathbb{Z}_3\), [4] = [1]. Así que escribimos

\([2] \odot [2] = [4] = [1]\)

Las tablas completas de suma y multiplicación para\(\mathbb{Z}_3\) son

Comprobación de progreso 7.20 (Aritmética Modular en\(\mathbb{Z}_2\), \(\mathbb{Z}_5\), and \(\mathbb{Z}_6\))

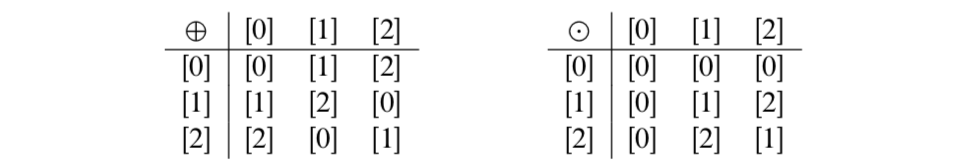
1. Construir tablas de suma y multiplicación para\(\mathbb{Z}_2\), los enteros módulo 2.
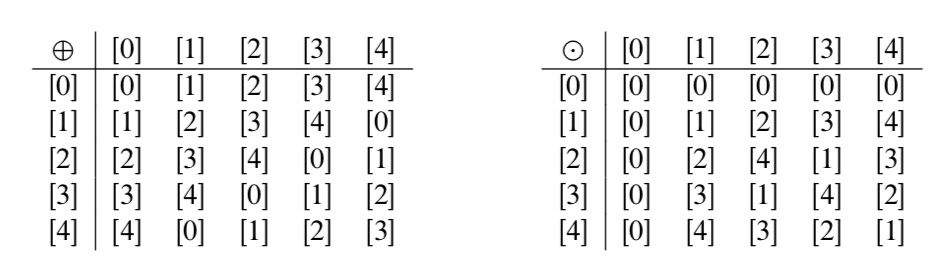
2. Verificar que las siguientes tablas de suma y multiplicación para\(\mathbb{Z}_5\) sean correctas.
   
3. Construir tablas completas de suma y multiplicación para\(\mathbb{Z}_6\).
4. En los enteros, la siguiente declaración es verdadera. A veces llamamos a esto la propiedad cero del producto para los enteros.
   Para todos\(a, b \in \mathbb{Z}\), si\(a \cdot b = 0\), entonces\(a = 0\) o\(b = 0\).
   Escriba el contrapositivo de la declaración condicional en esta propiedad.
5. ¿Son verdaderas o falsas las siguientes afirmaciones? Justifica tus conclusiones.
   
   (a) Para todos\([a], [b] \in \mathbb{Z}_5\), si\([a] \odot [b] = [0]\), entonces\([a] = [0]\) o\([b] = [0]\).
   b) Para todos\([a], [b] \in \mathbb{Z}_6\), si\([a] \odot [b] = [0]\), entonces\([a] = [0]\) o\([b] = [0]\).

Responder

Agrega textos aquí. No elimine primero este texto.

Pruebas de Divisibilidad

La aritmética de congruencia se puede utilizar para probar ciertas pruebas de divisibilidad. Por ejemplo, es posible que hayas aprendido que un número natural es divisible por 9 si la suma de sus dígitos es divisible por 9. Como ejemplo fácil, nótese que la suma de los dígitos de 5823 es igual a\(5 + 8 + 2 + 3 = 18\), y sabemos que 18 es divisible por 9. También se puede verificar que 5823 es divisible por 9. (El cociente es 647.) De hecho, podemos generalizar esta propiedad tratando con restos cuando un número natural se divide por 9.

Dejar\(n \in \mathbb{N}\) y dejar s.n/ denotar la suma de los dígitos de\(n\). Por ejemplo, si\(n = 7319\), entonces\(s(7319) = 7 + 3 + 1 + 9 = 20\). En Preview Activity\(\PageIndex{2}\), vimos que

\(7319 \equiv 2\)(mod 9) y\(20 \equiv 2\) (mod 9).

De hecho, por cada ejemplo en Preview Activity\(\PageIndex{2}\), vimos que n y s.n/ eran congruentes módulo 9 ya que ambos tenían el mismo resto al dividirse por 9. Los conceptos de congruencia y clases de congruencia pueden ayudar a demostrar que esto siempre es cierto.

Utilizaremos el caso de\(n = 7319\) para ilustrar el proceso general. Debemos utilizar nuestro sistema estándar de valor posicional. Con esto, queremos decir que escribiremos 7319 de la siguiente manera:

\[7319 = (7 \times 10^3) + (3 \times 10^2) + (1 \times 10^1) + (9 \times 10^0).\]

La idea es ahora usar la definición de suma y multiplicación en\(\mathbb{Z}_9\) para convertir la ecuación (7.4.3) en una ecuación en\(\mathbb{Z}_9\). Hacemos esto de la siguiente manera:

\[\begin{array} {rcl} {[7319]} &= & {[(7 \times 10^3) + (3 \times 10^2) + (1 \times 10^1) + (9 \times 10^0)]} \\ {} &= & {[7 \times 10^3] \oplus [3 \times 10^2] \oplus [1 \times 10^1] \oplus [9 \times 10^0]} \\ {} &= & {([7] \odot [10^3]) \oplus ([3] \odot [10^2]) \oplus ([1] \odot [10^1]) \oplus ([9] \odot [1]).} \end{array}\]

Desde\(10^3 \equiv 1\) (mod 9),\(10^2 \equiv 1\) (mod 9) y\(10 \equiv 1\) (mod 9), podemos concluir que\([10^3] = [1]\),\([10^2] = [1]\) y\([10] = [1]\). Por lo tanto, podemos usar estos hechos y la ecuación (7.4.4) para obtener

\[\begin{array} {rcl} {[7319]} &= & {([7] \odot [10^3]) \oplus ([3] \odot [10^2]) \oplus ([1] \odot [10]) \oplus ([9] \odot [1])} \\ {} &= & {([7] \odot [1]) \oplus ([3] \odot [1]) \oplus ([1] \odot [1]) \oplus ([9] \odot [1])} \\ {} &= & {[7] \oplus [3] \oplus [1] \oplus [9]} \\ {} &= & {[7 + 3 + 1 + 9].} \end{array}\]

La ecuación (7.4.5) nos dice que 7319 tiene el mismo resto cuando se divide por 9 como la suma de sus dígitos. Es fácil comprobar que la suma de los dígitos es 20 y por lo tanto tiene un resto de 2. Esto quiere decir que cuando 7319 se divide por 9, el resto es 2.

Para probar que cualquier número natural tiene el mismo resto cuando se divide por 9 como la suma de sus dígitos, es útil introducir notación para la representación decimal de un número natural. La notación que usaremos es similar a la notación para el número 7319 en la ecuación (7.4.3).

En general, si\(n \in \mathbb{N}\), y\(n = a_{k}a_{k - 1} \cdot\cdot\cdot a_{1}a_{0}\) es la representación decimal de\(n\), entonces

\(n = (a_k \times 10^{k}) + (a_{k - 1} \times 10^{k-1}) + \cdot\cdot\cdot + (a_{1} \times 10^{1}) + (a_{0} \times 10^{0}).\)

Esto también se puede escribir usando la notación de suma de la siguiente manera:

\(n = \sum_{j = 0}^{k} (a_{j} \times 10^{j}).\)

Usando clases de congruencia para congruencia módulo 9, tenemos

\[\begin{array} {rcl} {[n]} &= & {[(a_k \times 10^{k}) + (a_{k - 1} \times 10^{k-1}) + \cdot\cdot\cdot + (a_{1} \times 10^{1}) + (a_{0} \times 10^{0})]} \\ {} &= & {[a_k \times 10^{k}] \oplus [a_{k - 1} \times 10^{k-1}] \oplus \cdot\cdot\cdot \oplus [a_{1} \times 10^{1}] \oplus [a_{0} \times 10^{0}]} \\ {} &= & {([a_k] \odot [10^k]) \oplus ([a_{k - 1}] \odot [10^{k - 1}]) \oplus \cdot\cdot\cdot \oplus ([a_1] \odot [10^{1}]) \oplus ([a_0] \odot [10^{0}]).} \end{array}\]

Se necesita un último detalle. Se da en la Proposición 7.21. La prueba por inducción matemática es Ejercicio (6).

Proposición 7.21.

Si\(n\) es un entero no negativo, entonces\(10^{n} \equiv 1\) (mod 9), y por lo tanto para la relación de equivalencia de congruencia módulo 9,\([10^{n}] = [1]\).

Si dejamos\(s(n)\) denotar la suma de los dígitos de\(n\), entonces

\(s(n) = a_k + a_{k - 1} + \cdot\cdot\cdot + a_1 + a_0.\)

Ahora usando la ecuación (7.4.6) y la Proposición 7.21, obtenemos

\[\begin{array} {rcl} {[n]} &= & {([a_k] \odot [1]) \oplus ([a_{k - 1}] \odot [1]) \oplus \cdot\cdot\cdot \oplus ([a_1] \odot [1]) \oplus ([a_0] \odot [1])} \\ {} &= & {[a_k] \oplus [a_{k - 1}] \oplus \cdot\cdot\cdot \oplus [a_1] \oplus [a_0] \\ {} &= & {[a_k + a_{k-1} + \cdot\cdot\cdot + a_1 + a_0].} \\ {} &= & {[s(n)].} \end{array}\]

Esto completa la prueba del Teorema 7.22.

Teorema 7.22.

Dejar\(n \in \mathbb{N}\) y dejar\(s(n)\) denotar la suma de los dígitos de\(n\). Entonces

1. \([n] = [s(n)]\), utilizando clases de congruencia módulo 9.
2. \(n \equiv s(n)\)(mod 9)
3. \(9\ |\ n\)si y sólo si\(9\ |\ s(n)\).

La parte (3) del Teorema 7.22 se denomina prueba de divisibilidad. Si da una condición necesaria y suficiente para que un número natural sea divisible por 9. En los ejercicios se explorarán otras pruebas de divisibilidad. La mayoría de estas pruebas de divisibilidad pueden probarse de manera similar a la prueba de la prueba de divisibilidad para 9.

Ejercicio 7.4

1. (a) Completar las tablas de suma y multiplicación para\(\mathbb{Z}_4\).
   (b) Completar las tablas de suma y multiplicación para\(\mathbb{Z}_7\).
   (c) Completar las tablas de suma y multiplicación para\(\mathbb{Z}_8\).
2. El conjunto\(\mathbb{Z}_n\) contiene\(n\) elementos. Una forma de resolver una ecuación en\(\mathbb{Z}_n\) es sustituir cada uno de estos\(n\) elementos en la ecuación para verificar cuáles son soluciones. En\(\mathbb{Z}_n\), cuando no se utilizan paréntesis, seguimos el orden habitual de las operaciones, lo que significa que las multiplicaciones se hacen primero y luego las adiciones. Resolver cada una de las siguientes ecuaciones:
   
   (a)\([x]^2 = [1]\) en\(\mathbb{Z}_4\)
   (b)\([x]^2 = [1]\) en\(\mathbb{Z}_8\)
   (c)\([x]^4 = [1]\) en\(\mathbb{Z}_5\)
   (d)\([x]^2 \oplus [3] \odot [x] = [3]\) en\(\mathbb{Z}_6\)
   (e)\([x]^2 \oplus [1] = [0]\) en \(\mathbb{Z}_5\)
   (f)\([3] \odot [x] \oplus [2] = [0]\) en\(\mathbb{Z}_5\)
   (g)\([3] \odot [x] \oplus [2] = [0]\) en\(\mathbb{Z}_6\)
   (h)\([3] \odot [x] \oplus [2] = [0]\) en\(\mathbb{Z}_9\)
3. En cada caso, determinar si la declaración es verdadera o falsa.
   
   (a) Para todos\([a] \in \mathbb{Z}_6\)\([a] \ne [0]\), si, entonces existe\([b] \in \mathbb{Z}_6\) tal que\([a] \odot [b] = [1]\).
   b) Para todos\([a] \in \mathbb{Z}_5\), si\([a] \ne [0]\), entonces existe\([b] \in \mathbb{Z}_5\) tal que\([a] \odot [b] = [1]\).
4. En cada caso, determinar si la declaración es verdadera o falsa.
   
   (a) Para todos\([a], [b] \in \mathbb{Z}_6\), si\([a] \ne [0]\) y\([b] \ne [0]\), entonces\([a] \odot [b] \ne [0]\).
   b) Para todos\([a], [b] \in \mathbb{Z}_5\), si\([a] \ne [0]\) y\([b] \ne [0]\), entonces\([a] \odot [b] \ne [0]\).
5. a) Demostrar la siguiente proposición:
   Para cada uno\([a] \in \mathbb{Z}_5\), si\([a] \ne [0]\), entonces\([a]^2 = [1]\) o\([a]^2 = [4]\).
   b) ¿Existe un entero\(a\) tal que\(a^2 = 5, 158, 232, 468, 953, 153\)? Utilice su trabajo en la Parte (a) para justificar su conclusión. Comparar con Ejercicio (10) en la Sección 3.5.
6. Utilizar la inducción matemática para probar la Proposición 7.21.
   Si\(n\) es un entero no negativo, entonces\(10^n \equiv 1\) (mod 9), y por lo tanto para la relación de equivalencia de congruencia módulo 9,\([10^n] = [1]\).
7. Usa la inducción matemática para demostrar que si\(n\) es un entero no negativo, entonces\(10^n \equiv 1\) (mod 3). De ahí que para las clases de congruencia módulo 3, si n es un entero no negativo, entonces\([10^n] = [1]\).
8. Dejar\(n \in \mathbb{N}\) y dejar\(s(n)\) denotar la suma de los dígitos de\(n\) .Entonces si escribimos
   \[n = (a_k \times 10^k\) + (a_{k - 1} \times 10^{k - 1} + \cdot\cdot\cdot + (a_1 \times 10^{1}) + (a_0 \times 10^{0}).\]
   entonces\(s(n) = a_k + a_{k - 1} + \cdot\cdot\cdot + a_1 + a_0\). Utilizar el resultado en el Ejercicio (7) para ayudar a probar cada uno de los siguientes:
   
   (a)\([n] = [s(n)]\), utilizando clases de congruencia módulo 3.
   b)\(n \equiv s(n)\) (mod 3).
   c)\(3\ |\ n\) si sólo si\(3\ |\ s(n)\).
9. Usa la inducción matemática para demostrar que si\(n\) es un número entero y\(n ge 1\), entonces\(10^n \equiv 0\) (mod 5). De ahí, para clases de congruencia módulo 5, si\(n\) es un número entero y\(n \ge 1\), entonces\([10^n] = [0]\).
10. Dejar\(n \in \mathbb{N}\) y asumir
    \[n = (a_k \times 10^k) + (a_{k - 1} \times 10^{k - 1} + \cdot\cdot\cdot + (a_1 \times 10^{1}) + (a_0 \times 10^{0}).\]
    Utilizar el resultado en el Ejercicio (9) para ayudar a probar cada uno de los siguientes:
    
    (a)\([n] = [a_0]\), utilizando clases de congruencia módulo 5.
    b)\(n \equiv a_0\) (mod 5).
    c)\(5\ |\ n\) si sólo si\(5\ |\ a_0\).
11. Usa la inducción matemática para demostrar que si\(n\) es un número entero y\(n ge 2\), entonces\(10^n \equiv 0\) (mod 4). De ahí, para clases de congruencia módulo 4, si\(n\) es un número entero y\(n \ge 2\), entonces\([10^n] = [0]\).
12. Dejar\(n \in \mathbb{N}\) y asumir
    \[n = (a_k \times 10^k) + (a_{k - 1} \times 10^{k - 1} + \cdot\cdot\cdot + (a_1 \times 10^{1}) + (a_0 \times 10^{0}).\]
    Utilizar el resultado en el Ejercicio (11) para ayudar a probar cada uno de los siguientes:
    
    (a)\([n] = [10a_1 + a_0]\), utilizando clases de congruencia módulo 4.
    b)\(n \equiv (10a_1 + a_0)\) (mod 5).
    c)\(4\ |\ n\) si sólo si\(4\ |\ (10a_1 + a_0)\).
13. Usa la inducción matemática para demostrar que si\(n\) es un entero y\(n ge 3\), entonces\(10^n \equiv 0\) (mod 8). De ahí, para clases de congruencia módulo 8, si\(n\) es un número entero y\(n \ge 3\), entonces\([10^n] = [0]\).
14. Dejar\(n \in \mathbb{N}\) y asumir
    \[n = (a_k \times 10^k) + (a_{k - 1} \times 10^{k - 1} + \cdot\cdot\cdot + (a_1 \times 10^{1}) + (a_0 \times 10^{0}).\]
    Utilizar el resultado en el Ejercicio (13) para ayudar a desarrollar una prueba de divisibilidad para 8. Demuestra que tu prueba de divisibilidad es correcta.
15. Usa la inducción matemática para demostrar que si\(n\) es un entero no negativo entonces\(10^n \equiv (-1)^n (mod 11)\). De ahí, para clases de congruencia módulo 11, si\(n\) es un entero no negativo, entonces\([10^n] = [(-1)^n]\).
16. Dejar\(n \in \mathbb{N}\) y asumir
    \[n = (a_k \times 10^k) + (a_{k - 1} \times 10^{k - 1} + \cdot\cdot\cdot + (a_1 \times 10^{1}) + (a_0 \times 10^{0}).\]
    Utilizar el resultado en el Ejercicio (15) para ayudar a probar cada uno de los siguientes:
    
    (a)\(n \equiv \sum_{j = 0}^{k} (-1)^j a_j\) (mod 11).
    (b)\([n] = [\sum_{j = 0}^{k} (-1)^j a_j]\), utilizando clases de congruencia módulo 11.
    c) 11 divide\(n\) si y sólo si 11 divide\(\sum_{j = 0}^{k} (-1)^j a_j\)
17. a) Demostrar la siguiente proposición:
    Para todos\([a], [b] \in \mathbb{Z}_3\), si\([a]^2 + [b]^2 = [0]\), entonces\([a] = 0\) y\([b] = [0]\).
    b) Utilizar el Ejercicio (17a) para acreditar la siguiente proposición:
    Vamos\(a, b \in \mathbb{Z}\). Si\((a^2 + b^2) \equiv 0\) (mod 3), entonces\(a \equiv 0\) (mod 3) y\(b \equiv 0\) (mod 3).
    (c) Utilice el Ejercicio (17b) para probar la siguiente proposición:
    Dejar\(a, b \in \mathbb{Z}\), si 3 divide\((a^2 + b^2)\), entonces 3 divide\(a\) y 3 divide\(b\).
18. Demostrar la siguiente proposición:
    Para cada uno\(a \in \mathbb{Z}\), si existen enteros\(b\) y\(c\) tal que\(a = b^4 + c^4\), entonces las unidades dígito de\(a\) deben ser 0, 1, 2, 5, 6 o 7.
19. ¿La siguiente proposición es verdadera o falsa? Justifica tu conclusión.
    Para\(n \in \mathbb{Z}\). Si\(n\) es impar, entonces\(8\ |\ (n^2 - 1)\). Pista: ¿Cuáles son los valores posibles de\(n\) (mod 8)?
20. Demostrar la siguiente proposición:
    Por\(n \in \mathbb{Z}\). Si\(n \equiv 7\) (mod 8), entonces no\(n\) es la suma de tres cuadrados. Es decir, no existen números naturales\(a\),\(b\), y\(c\) tal que\(n = a^2 + b^2 + c^2\).
    
    Exploraciones y actividades
21. Usando Congruencia Modulo 4. El conjunto\(\mathbb{Z}_n\) es un conjunto finito y, por lo tanto, una forma de probar las cosas\(\mathbb{Z}_n\) es simplemente usar los\(n\) elementos\(\mathbb{Z}_n\) como\(n\) casos para una prueba usando casos. Por ejemplo, si\(n \in \mathbb{Z}\), entonces en\(\mathbb{Z}_4\),\([n] = [0]\),\([n] = [1]\),\([n] = [2]\), o\([n] = [3]\).
    
    (a) Demostrar que si\(n \in \mathbb{Z}\), entonces en\(\mathbb{Z}_4\),\([n]^2 = [0]\) o\([n]^2 = [1]\). Use esto para concluir que en\(\mathbb{Z}_4\),\([n^2] = [0]\) o\([n^2] = [1]\).
    (b) Traducir las ecuaciones\([n^2] = [0]\) y\([n^2] = [1]\)\(\mathbb{Z}_4\) en congruencias módulo 4.
    (c) Utilizar un resultado en el Ejercicio (12) para determinar el valor de\(r\) para que\(r \in \mathbb{Z}\),\(0 \le r < 3\), y Es
    \[104\ 257\ 833\ 259 \equiv r \text{ (mod 4).}\]
    decir,\([104\ 257\ 833\ 259] = [r]\) en\(\mathbb{Z}_4\).
    d) ¿Es el número natural 104 257 833 259 un cuadrado perfecto? Justifica tu conclusión.

Responder

Agrega textos aquí. No elimine primero este texto.