1.7: Relaciones
- Page ID
- 114049
Una de las principales formas en que la escritura matemática difiere de la escritura ordinaria es en su increíble brevedad. Por ejemplo, una tesis de doctorado para alguien en humanidades sería muy sospechosa si su longitud fuera menor que\(300\) las páginas, mientras que sería bastante aceptable que un estudiante de doctorado en matemáticas presentara una tesis de menos de\(100\) páginas. En efecto, el criterio habitual para una tesis doctoral (o de hecho cualquier trabajo académico en matemáticas) es que sea “nueva, verdadera e interesante”. Si uno puede demostrar un resultado verdaderamente interesante y novedoso en una sola página, probablemente entreguen la piel de oveja.
¿Cómo se logra esta gran brevedad? ¡Insertando símbolos únicos en lugar de palabras de todo un párrafo! Una clase de símbolos en particular tiene un poder inmenso, los llamados símbolos relacionales. Cuando colocas un símbolo relacional entre dos expresiones, creas una oración que dice que la relación se mantiene. ¡Probablemente debería pronunciarse el periodo al final de la última frase! “¡La relación se mantiene, punto!” En otras palabras, cuando escribes una oración matemática que involucra una relación, estás afirmando que la relación es True (el capital\(\text{T}\) es intencional). Por eso está bien escribir “\(2 < 3\)” pero no está bien escribir “”\(3 < 2\). El símbolo\(<\) es un símbolo de relación y se supone que solo debes ponerlo entre dos cosas cuando realmente llevan esta relación entre sí.
La situación se vuelve un poco más complicada cuando tenemos variables en expresiones relacionales, pero antes de proceder a considerar esa complicación hagamos una lista de las relaciones que hemos visto hasta la fecha:
\(=,\; <,\; >,\; ≤,\; ≥,\; |, \text{ and } ≡ (\text{mod } m).\)
Cada uno de estos, cuando se coloca entre números, produce una declaración que es verdadera o falsa. Normalmente no escribiríamos los falsos, sino que deberíamos expresar que sabemos que la relación no se sostiene negando el símbolo de relación (a menudo dibujando una barra a través de él, pero algunos de los símbolos anteriores son negaciones de otros).
Entonces, ¿qué pasa con las expresiones que involucran variables y estos símbolos de relación? Por ejemplo, ¿qué significa\(x < y\) realmente? Bien, sé que sabes lo que\(x < y\) significa pero, filosóficamente, un símbolo de relación que involucra variables está haciendo algo de lo que quizás solo hayas estado vagamente consciente en el pasado —es introducir una suposición. ¡Cuidado con los símbolos de relación que involucran variables! Siempre que los encuentres significa que las reglas del juego se están alterando sutilmente —hasta el punto en que veas\(x < y\),\(x\) y\(y\) son solo dos números aleatorios, pero después de ese punto debemos suponer que\(x\) es el menor de los dos.
Las relaciones que hemos discutido hasta ahora son relaciones binarias, es decir, van entre dos números. También hay relaciones de orden superior. Por ejemplo, una famosa relación ternaria (una relación entre tres cosas) es la noción de “entretenimiento”. Si\(A\),\(B\) y\(C\) son tres puntos los cuales se encuentran todos en una sola línea, escribimos\(A \star B \star C\) si\(B\) cae en algún lugar del segmento de línea\(\overline{AC}\). Entonces el símbolo\(A \star B \star C\) es la taquigrafía de la oración “El punto\(B\) se encuentra en algún lugar entre puntos\(A\) y\(C\) en la línea determinada por ellos”.
Hay una tendencia un poco tonta en estos días a definir funciones como una clase especial de relaciones. (Esto es un poco tonto no porque esté mal —de hecho, las funciones son un tipo especial de relación—, sino porque es el enfoque menos intuitivo posible, y suele ser frustrado en estudiantes de secundaria o preparatoria). Cuando se toma este enfoque, primero definimos una relación como cualquier conjunto de pares ordenados y luego establecemos una restricción sobre los pares ordenados que pueden estar en una relación si va a ser una función. Claramente de lo que están hablando estos autores de libros de texto de Álgebra son relaciones binarias, una relación ternaria sería en realidad un conjunto de triples ordenados, y las relaciones de orden superior podrían involucrar\(4\) -tuplas o\(5\) -tuplas ordenadas, etc. Un par de pequeños ejemplos deberían ayudar a aclarar esto conexión entre un símbolo de relación y algún conjunto de tuplas.
Considere los números de\(1\) a\(5\) y la relación menor que,\(<\). Como conjunto de pares ordenados, esta relación es el conjunto
\(\{(1, 2),(1, 3),(1, 4),(1, 5),(2, 3),(2, 4),(2, 5),(3, 4),(3, 5),(4, 5)\}.\)
Los pares que están en la relación son aquellos tales que el primero es menor que el segundo.
Un ejemplo que involucra la relación ternaria “entretenimientos” se puede tener a partir del siguiente diagrama.
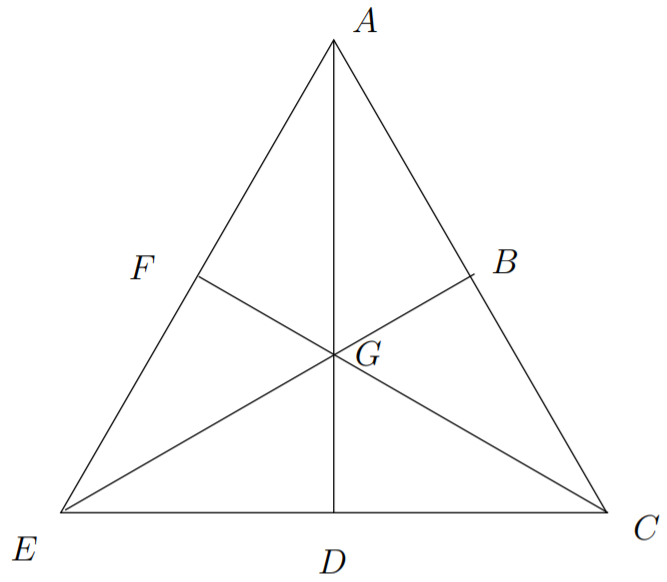
La relación entre los puntos de este diagrama consta de las siguientes triples.
\(\{(A, B, C),(A, G, D),(A, F, E),(B, G, E),(C, B, A),(C, G, F),(C, D, E), (D, G, A),(E, D, C),(E, G, B),(E, F, A),(F, G, C)\}\).
Al pensar en una función como un tipo especial de relación, los pares son de la forma\((x, f(x))\). Es decir, consisten en una entrada y la salida correspondiente. ¿Cuál es la restricción que se debe poner a los pares en una relación si va a ser una función? (Pista: piensa en la llamada prueba de línea vertical.)
Ejercicios
Considera los números del\(1\) al\(10\). Dar el conjunto de pares de estos números que corresponda a la relación de divisibilidad.
El dominio de una función (o relación binaria) es el conjunto de números que aparecen en la primera coordenada. El rango de una función (o relación binaria) es el conjunto de números que aparecen en la segunda coordenada.
Considera el conjunto\(\{0, 1, 2, 3, 4, 5, 6\}\) y la función\(f(x) = x^2 (\text{ mod } 7)\). Expresar esta función como una relación escribiendo explícitamente el conjunto de pares ordenados que contiene. ¿Cuál es el rango de esta función?
¿Qué relación en los números de\(1\) a\(10\) representa el siguiente conjunto de pares ordenados?
\(\{(1, 1),(1, 2),(1, 3),(1, 4),(1, 5),(1, 6),(1, 7),(1, 8),(1, 9),(1, 10),\)
\((2, 2),(2, 3),(2, 4),(2, 5),(2, 6),(2, 7),(2, 8),(2, 9),(2, 10),\)
\((3, 3),(3, 4),(3, 5),(3, 6),(3, 7),(3, 8),(3, 9),(3, 10),\)
\((4, 4),(4, 5),(4, 6),(4, 7),(4, 8),(4, 9),(4, 10),\)
\((5, 5),(5, 6),(5, 7),(5, 8),(5, 9),(5, 10),\)
\((6, 6),(6, 7),(6, 8),(6, 9),(6, 10),\)
\((7, 7),(7, 8),(7, 9),(7, 10),\)
\((8, 8),(8, 9),(8, 10),\)
\((9, 9),(9, 10),\)
\((10, 10)\}\)
Dibuja una estrella de cinco puntas, etiqueta todos los\(10\) puntos. Hay\(40\) triples de estas etiquetas que satisfacen la relación entre medias. Enumerarlos.
Esbozar una gráfica de la relación
\(\{(x, y) x, y ∈ R \text{ and } y > x^2\}\).
Se dice que una función\(f(x)\) es invertible si hay otra función\(g(x)\) tal que\(g(f(x)) = x\) para todos los valores de\(x\). (Por lo general, la función inversa, se\(g(x)\) denotaría\(f^{−1} (x)\).) Supongamos que se le presenta una función como una relación —es decir, se le acaba de dar un conjunto de pares. ¿Cómo se puede distinguir si la función representada por esta lista de pares de entrada/salida es invertible? ¿Cómo se puede producir la inversa (como un conjunto de pares ordenados)?
Hay una relación conocida como “tiene color” que va desde el conjunto
\(F = \{\text{orange}, \text{ cherry} , \text{ pumpkin} , \text{ banana}\}\)
al conjunto
\(C = \{\text{orange}, \text{ red}, \text{ green}, \text{ yellow}\}.\)
¿Qué pares están en “tiene color”?