2.3: Equivalencias lógicas
- Page ID
- 114059
Algunas declaraciones lógicas son “lo mismo”. Por ejemplo, en el último apartado, discutimos el hecho de que un condicional y su contrapositivo tienen el mismo contenido lógico. ¿No estaríamos justificados por escribir algo como lo siguiente?
\(A \implies B = ¬B \implies ¬A\)
Bueno, una objeción bastante seria a hacer eso es que el signo de iguales ya\((=)\) tiene trabajo; se usa para indicar que dos cantidades numéricas son iguales. ¡Lo que estamos haciendo aquí es realmente algo diferente! Sin embargo, existe un concepto de “igualdad” entre ciertos enunciados compuestos, y necesitamos una forma simbólica de expresarlo. Hay dos notaciones de uso común. La notación que parece preferir los logísticos es la bicondicional\((\iff)\). La notación que usaremos en el resto de este libro es un signo de igual con un poco de decoración extra en él\((\cong)\).
Así podemos escribir
\((A \implies B) \iff (¬B \implies ¬A)\)
o
\(A \implies B \cong ¬B \implies ¬A.\)
A mí me gusta este último, pero usa la forma que quieras — nadie va a tener ningún problema para entender tampoco.
La definición formal de equivalencia lógica, que es lo que hemos estado describiendo, es la siguiente: dos oraciones compuestas son lógicamente equivalentes si en una tabla de verdad (que contiene todas las combinaciones posibles de los valores de verdad de las variables predicadas en sus filas) los valores de verdad de las dos oraciones son iguales en cada fila.
Considere las dos oraciones compuestas\(A ∨ B\) y\(A ∨ (¬A ∧ B)\). Hay un total de variables\(2\) predicadas entre ellas, por lo que bastará con una tabla de verdad con\(4\) filas. Rellene las entradas faltantes en la tabla de verdad y determine si las declaraciones son equivalentes.
| \(A\) | \(B\) | \(A ∨ B\) | \(A ∨ (¬A ∧ B)\) |
|---|---|---|---|
| \ (A\) ">\(T\) | \ (B\) ">\(T\) | \ (A; A; B;) "> | \ (A;;;;;;;;;;;) "> |
| \ (A\) ">\(T\) | \ (B\) ">\(\phi\) | \ (A; A; B;) "> | \ (A;;;;;;;;;;;) "> |
| \ (A\) ">\(\phi\) | \ (B\) ">\(T\) | \ (A; A; B;) "> | \ (A;;;;;;;;;;;) "> |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\phi\) | \ (A; A; B;) "> | \ (A;;;;;;;;;;;) "> |
Uno podría, en principio, verificar todas las equivalencias lógicas rellenando tablas de verdad. En efecto, en los ejercicios para esta sección, te pediremos que desarrolles una cierta facilidad en esta tarea. Si bien esta actividad puede ser algo divertida, y muchos de mis alumnos quieren que el relleno de tablas de verdad sea una parte importante de su examen de mitad de período, probablemente eventualmente llegarás a encontrarlo algo tedioso. Un enfoque un poco más maduro de las equivalencias lógicas es este: utilizar un conjunto de equivalencias básicas —que a su vez pueden verificarse a través de tablas de verdad— como reglas básicas o leyes de equivalencia lógica, y desarrollar una estrategia para convertir una oración en otra usando estas reglas. Este proceso se sentirá muy familiar, es como “hacer” álgebra, pero las reglas que uno está permitido usar son sutilmente diferentes.
Primero, tenemos las leyes conmutativas, una para cada una de conjunción y disyunción. Vale la pena señalar que no existe una ley conmutativa para la implicación.
Eso dice la propiedad conmutativa de la conjunción\(A∧B \cong B ∧A\). Esta es una afirmación bastante aparente desde la perspectiva de la lingüística. Seguramente es lo mismo decir “el clima es frío y nevado” como es decir “el clima es nevado y frío”. Esta propiedad conmutativa también es clara desde la perspectiva de los circuitos lógicos digitales.
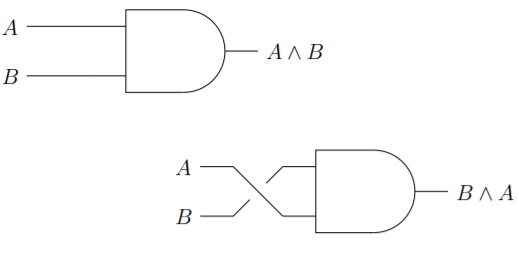
La propiedad conmutativa de las disyunciones es igualmente transparente desde la perspectiva de un diagrama de circuito.
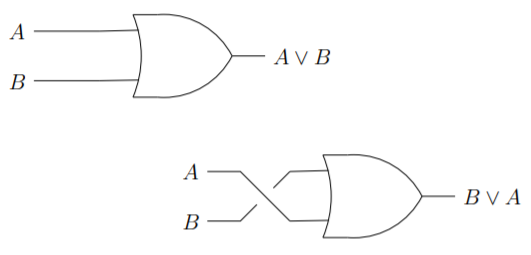
Las leyes asociativas también tienen algo que ver con lo que se realizan las operaciones de orden. Se podría pensar en la diferencia en los siguientes términos: Las propiedades conmutativas involucran orden espacial o físico y las propiedades asociativas involucran orden temporal. La ley asociativa de suma podría usarse para decir que obtendremos el mismo resultado si agregamos\(2\) y\(3\) primero, luego agregamos\(4\), o si agregamos\(2\) a la suma de\(3\) y\(4\) (es decir, que\((2+3)+4\) es lo mismo que\(2+ (3+4)\).) Tenga en cuenta que físicamente, los números están en el mismo orden (\(2\)entonces\(3\) entonces\(4\)) en ambas expresiones pero que los paréntesis indican una precedencia en cuando se evalúan los signos más.
La ley asociativa de conjunción establece que\(A∧(B ∧C) \cong (A∧B)∧C\). En términos visuales, esto significa que los siguientes dos diagramas de circuito son equivalentes.
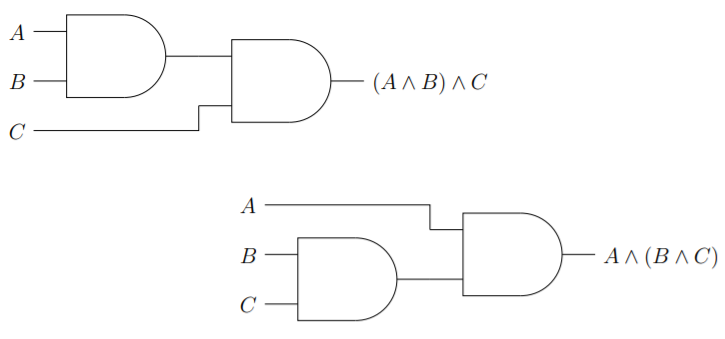
La ley asociativa de disyunción establece que\(A∨(B ∨ C) \cong (A∨B)∨ C\). Visualmente, esto se ve así:
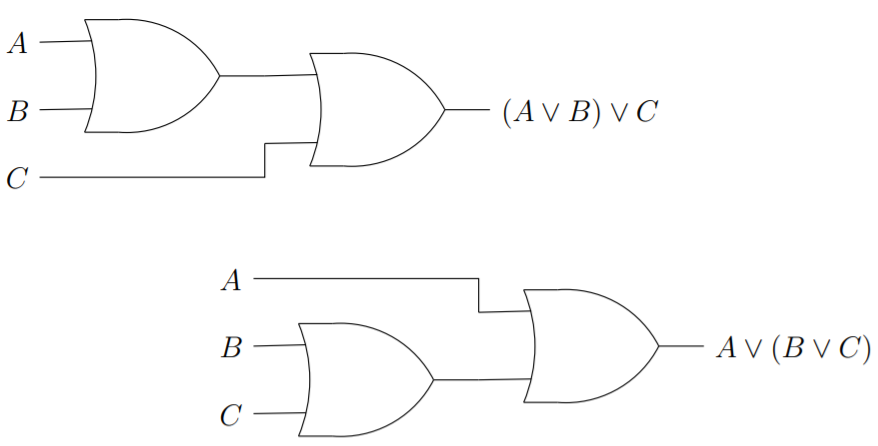
En una situación en la que tanto la asociatividad como la conmutatividad pertenecen los símbolos involucrados pueden aparecer en cualquier orden y con cualquier paréntesis razonable. ¿De cuántas maneras diferentes se\(2 + 3 + 4\) puede expresar la suma? Consideremos únicamente expresiones que estén completamente entre paréntesis.
El siguiente tipo de equivalencias lógicas básicas que consideraremos son las llamadas leyes distributivas. Las leyes distributivas implican la interacción de dos operaciones, cuando distribuimos la multiplicación sobre una suma, reemplazamos efectivamente una instancia de un operando y el operador asociado, por dos instancias, como se ilustra a continuación.
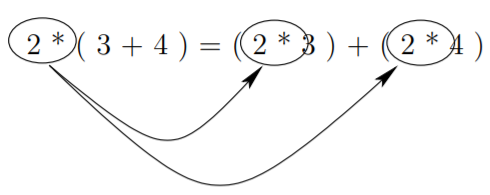
Cada uno de los operadores lógicos se distribuyen sobre el otro. Así tenemos la ley distributiva de conjunción sobre disyunción, que se expresa en la equivalencia\(A ∧ (B ∨ C) \cong (A ∧ B) ∨ (A ∧ C)\) y en el siguiente diagrama de circuito lógico digital.
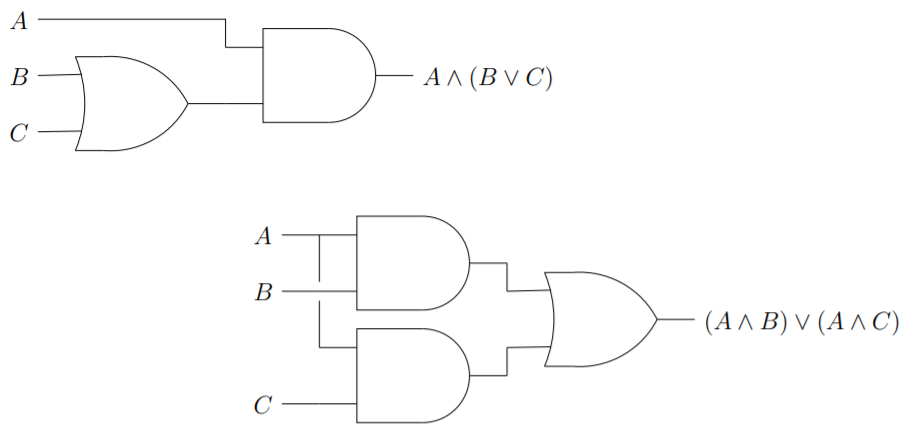
También tenemos la ley distributiva de disyunción sobre conjunción que viene dada por la equivalencia\(A ∨ (B ∧ C) \cong (A ∨ B) ∧ (A ∨ C)\) y en el diagrama de circuito:
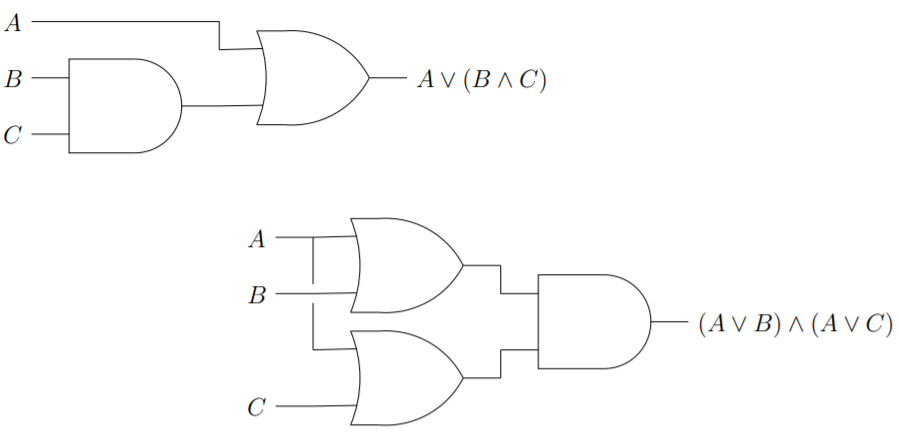
Tradicionalmente, las leyes que acabamos de exponer se llamarían leyes distributivas de izquierda y también necesitaríamos afirmar que existen leyes derecho-distributivas que se aplican. Ya que, en el escenario actual, ya hemos dicho que la ley conmutativa es válida, esto no es realmente necesario.
Declarar las versiones de la derecha de las leyes distributivas.
El siguiente conjunto de leyes que consideraremos proviene de tratar de averiguar a qué\((−(x + y) = −x + −y)\) debería corresponder la distribución de un signo menos sobre una suma en álgebra booleana. Al principio se puede suponer que lo análogo en el álgebra booleana sería algo así como\(¬(A∧B) \cong ¬A∧¬B\), pero podemos descartarlo fácilmente mirando una tabla de la verdad.
| \(A\) | \(B\) | \(¬(A ∧ B)\) | \(¬A ∧ ¬B\) |
|---|---|---|---|
| \ (A\) ">\(T\) | \ (B\) ">\(T\) | \ (¬ (A B)\) ">\(\phi\) | \ (¬A ¬B\) ">\(\phi\) |
| \ (A\) ">\(T\) | \ (B\) ">\(\phi\) | \ (¬ (A B)\) ">\(T\) | \ (¬A ¬B\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(T\) | \ (¬ (A B)\) ">\(T\) | \ (¬A ¬B\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\phi\) | \ (¬ (A B)\) ">\(T\) | \ (¬A ¬B\) ">\(T\) |
Lo que realmente funciona es un conjunto de reglas conocidas como leyes de DeMorgan, que básicamente dicen que se distribuye el signo negativo pero también se debe cambiar el operador. Como equivalencias lógicas, las leyes de DeMorgan son
\(¬(A ∧ B) \cong ¬A ∨ ¬B\)
y
\ (¬ (A) (A)\ cong ¬A ¬B.)
En la aritmética ordinaria, hay dos nociones de “inversa”. El negativo de un número se conoce como su inverso aditivo y el recíproco de un número es su inverso multiplicativo. Estas nociones conducen a un par de ecuaciones,
\(x + −x = 0\)
y
\(x · \dfrac{1}{x} = 1.\)
El álgebra booleana sólo tiene un concepto “inverso”, la negación de un predicado (es decir, negación lógica), pero las ecuaciones anteriores tienen análogos, al igual que los símbolos\(0\) y\(1\) que aparecen en ellos. Primero, considere la expresión booleana\(A ∨ ¬A\). Esto es lo lógico o de una declaración y su opuesto exacto; cuando uno es verdadero el otro es falso y viceversa. Pero, ¡la disyunción\(A ∨ ¬A\), siempre es verdad! Usamos el símbolo\(t\) (que significa tautología) para representar una oración compuesta cuyo valor de verdad es siempre verdadero. Una tautología (\(t\)) es
Álgebra booleana algo así como un cero (\(0\)) es a la aritmética. Pensamiento similar sobre la expresión booleana\(A ∧ ¬A\) lleva a la definición del símbolo\(c\) (que significa contradicción) para representar una oración que siempre es falsa. Las reglas que hemos estado discutiendo se conocen como leyes de complementariedad:
\(A ∨ ¬A \cong t\)y\(A ∧ ¬A \cong c\)
Ahora que tenemos las frases lógicas especiales representadas por\(t\) y\(c\) podemos presentar las llamadas leyes de identidad,\(A ∧ t \cong A\) y\(A ∨ c \cong A\). Si “y” una afirmación con algo que siempre es cierto, este nuevo compuesto tiene exactamente los mismos valores de verdad que el original. Si “o” una declaración con algo que siempre es falso, la nueva declaración compuesta tampoco se modifica con respecto a la original. Así, realizar una conjunción con una tautología no tiene ningún efecto —algo así como multiplicar por\(1\). Realizar una disyunción con una contradicción tampoco tiene ningún efecto —esto es algo parecido a sumar\(0\).
El número\(0\) tiene una propiedad especial:\(0 · x = 0\) es una ecuación que sostiene sin importar lo que\(x\) sea. Esto se conoce como una propiedad de dominación. Tenga en cuenta que no hay una regla de dominio que implique\(1\). En el lado booleano, tanto los símbolos\(t\) como\(c\) tienen reglas de dominación relacionadas.
\(A ∨ t \cong t\)y\(A ∧ c \cong c\)
En matemáticas, la palabra idempotente se emplea para describir situaciones en las que los poderes de una cosa son iguales a esa cosa. Por ejemplo, porque cada poder de\(1\) es\(1\), decimos que\(1\) es un idempotente. Ambas operaciones booleanas tienen relaciones de idempotencia que simplemente siempre funcionan (independientemente del operando). En álgebra ordinaria los idempotentes son muy raros (\(0\)y\(1\) son los únicos que vienen a la mente), pero en álgebra booleana cada declaración es equivalente a su cuadrado —donde el cuadrado de\(A\) puede interpretarse como\(A ∧ A\) o como\(A ∨ A\).
\(A ∨ A \cong A\)y\(A ∧ A \cong A\)
Hay un par de propiedades del operador de negación lógica que deben afirmarse, aunque probablemente parezcan evidentes. Si formas la negación de una negación, vuelves a lo mismo que el original; también los símbolos\(c\) y\(t\) son negaciones unas de otras.
\(¬(¬A) \cong A\)y\(¬t \cong c\)
Por último, debemos mencionar una propiedad realmente extraña, llamada absorción, que afirma que las expresiones\(A∧(A∨B)\) y en realidad\(A∨(A∧B)\) no tienen nada que ver con nada\(B\) en absoluto! Ambos de los enunciados anteriores son equivalentes a\(A\).
\(A ∧ (A ∨ B) \cong A\)y\(A ∨ (A ∧ B) \cong A\)
En el Cuadro 2.3.1, hemos recopilado todas estas equivalencias lógicas básicas en un solo lugar.
| Cuadro 2.3.1: Equivalencias Lógicas Básicas. | |||
|---|---|---|---|
| Versión Conjuntiva | Versión Disyuntiva | Analógico algebraico | |
| Leyes conmutativas | \(A∧B≅B∧A\) | \(A∨B≅B∨A\) | \(2+3=3+2\) |
| Leyes asociativas | \(A∧(B∧C)A∧(B∧C) ≅(A∧B)∧C\) | \(A∨(B∨C)A∨(B∨C) ≅(A∨B)∨C\) | \(2+(3+4)2+(3+4) =(2+3)+4\) |
| Leyes Distributivas | \(A∧(B∨C)≅A∧(B∨C)≅ \\(A∧B)∨(A∧C)\) | \(A∨(B∧C) ≅ \\ (A∨B)∧(A∨C)\) | \(2⋅(3+4)2⋅(3+4) =(2⋅3+2⋅4)\) |
| Leyes de DeMorgan | \(¬(A∧B)¬(A∧B) ≅¬A∨¬B\) | \(¬(A∨B)¬(A∨B) ≅¬A∧¬B\) | \(\text{none}\) |
| Doble negación | \(¬(¬A)≅A\) | \(\text{same}\) | \(−(−2)=2\) |
| Complementariedad | \(A∧¬A≅c\) | \(A∨¬A≅t\) | \(2+(−2)=0\) |
| Leyes de Identidad | \(A∧t≅A\) | \(A∨c≅A\) | \(7+0=7\) |
| Dominación | \(A∧c≅c\) | \(A∨t≅t\) | \(7⋅0=0\) |
| Idempotencia | \(A∧A≅A\) | \(A∨A≅A\) | \(1⋅1=1\) |
| Absorción | \(A∧(A∨B)≅A\) | \(A∨(A∧B)≅A\) | \(\text{none}\) |
Ejercicios:
Hay\(3\) operaciones utilizadas en álgebra básica (suma, multiplicación y exponenciación) y así existen leyes distributivas potencialmente\(6\) diferentes. Declarar todas las\(6\) “leyes” y determinar cuáles\(2\) son realmente válidas. (A modo de ejemplo, se vería la ley distributiva de la suma sobre la multiplicación\(x + (y · z) = (x + y) · (x + z)\), esta no es una de las verdaderas).
Utilice tablas de verdad para verificar o refutar las siguientes equivalencias lógicas.
- \((A ∧ B) ∨ B \cong (A ∨ B) ∧ B\)
- \(A ∧ (B ∨ ¬A) \cong A ∧ B\)
- \((A ∧ ¬B) ∨ (¬A ∧ ¬B) \cong (A ∨ ¬B) ∧ (¬A ∨ ¬B)\)
- Las leyes de absorción.
Dibuje pares de circuitos lógicos digitales relacionados que ilustren las leyes de DeMorgan.
Encuentra la negación de cada uno de los siguientes y simplifica lo más posible.
\((A ∨ B) \iff C\)
\((A ∨ B) \implies (A ∧ B)\)
Debido a que una sentencia condicional equivale a una cierta disyuntiva, y porque la ley de DeMorgan nos dice que la negación de una disyunción es una conjunción, se deduce que la negación de un condicional es una conjunción. Encuentra negaciones (la negación de una oración a menudo se llama su “negación”) para cada uno de los siguientes condicionales.
- “Si fumas, tendrás cáncer de pulmón”.
- “Si una sustancia brilla, no es necesariamente oro”.
- “Si hay humo, también debe haber fuego”.
- “Si se cuadra un número, el resultado es positivo”.
- “Si una matriz es cuadrada, es invertible”.
La llamada “ética de la reciprocidad” es una idea que ha surgido en muchas de las religiones y filosofías del mundo. A continuación se presentan declaraciones de la ética de varias fuentes. Discutir sus significados lógicos y determinar cuáles (si los hay) son lógicamente equivalentes.
- “Uno no debe comportarse con los demás de una manera que sea desagradable para uno mismo”. Mencio VII.A.4 (Hinduismo)
- “Ninguno de ustedes cree [de verdad] hasta que desee para su hermano lo que desea para sí mismo”. Número 13 del Imán “Cuarenta Hadices de Al-Nawawi”. (Islam)
- “Y como quisierais que los hombres os hicieran, haced también vosotros con ellos de la misma manera”. Lucas 6:31, Versión King James. (Cristianismo)
- “Lo que es odioso para ti, no lo hagas a tus semejantes. Esta es la ley: todo lo demás es comentario”. Talmud, Shabat 31a. (Judaísmo)
- “Y no daña a nadie, haz lo que quieras” (Wicca)
- “Lo que evitarías sufrir a ti mismo, buscarías no imponerle a los demás”. (el filósofo griego Epicteto — siglo I d.C.)
- “No hagas a los demás como esperas que ellos te hagan. Sus gustos pueden no ser los mismos”. (el dramaturgo irlandés George Bernard Shaw —\(20^{\text{th}}\) siglo d.C.)
Te encuentras con dos nativos de la tierra de caballeros y bribones. Rellenar una explicación para cada línea de las pruebas de sus identidades.
- Natasha dice: “Boris es un bridon”. Boris dice: “Natasha y yo somos caballeros”.
Reclamación: Natasha es un caballero, y Boris es un bridon.
Prueba: Si Natasha es un bridón, entonces Boris es un caballero.
Si Boris es un caballero, entonces Natasha es un caballero.
Por lo tanto, si Natasha es un bridon, entonces Natasha es un caballero.
De ahí que Natasha sea un caballero.
Por lo tanto, Boris es un bridon.
Q.E.D.
- Bonaparte dice “Yo soy un caballero y Wellington es un bridon”. Wellington dice “Te diría que B es un caballero”.
Reclamación: Bonaparte es un caballero y Wellington es un bridón.
Prueba: O Wellington es un bridón o Wellington es un caballero.
Si Wellington es un caballero se deduce que Bonaparte es un caballero.
Si Bonaparte es un caballero entonces Wellington es un bridon.
Entonces, si Wellington es un caballero entonces Wellington es un bridon (¡lo cual es imposible!)
Así, Wellington es un bridon.
Ya que Wellington es un bridón, su declaración “Yo te diría que Bonaparte es un caballero” es falsa.
Entonces Wellington de hecho nos diría que Bonaparte es un bridon.
Dado que Wellington es un bridón concluimos que Bonaparte es un caballero.
Así Bonaparte es un caballero y Wellington es un bridon (como se afirma).
Q.E.D.


