6.1: Relaciones
- Page ID
- 114106
Una relación en matemáticas es un símbolo que se puede colocar entre dos números (o variables) para crear una sentencia lógica (o oración abierta). El punto principal aquí es que la inserción de un símbolo de relación entre dos números crea una declaración cuyo valor es verdadero o falso. Por ejemplo, hemos visto previamente el símbolo de divisibilidad (\(|\)) y anotado el error común de confundirlo con el símbolo de división (\(/\)); uno de estos nos dice realizar una operación aritmética, el otro nos pregunta si si se realizara tal operación habría una resto. Hay muchos otros símbolos que hemos visto que tienen esta característica, el más importante es probablemente\(=\), pero hay muchos:\(\neq, <, \leq, >, ≥\) todos funcionan de esta manera —si los colocamos entre dos números obtenemos una cosa booleana, es verdad o falsa. Si, en lugar de números, pensamos en colocar conjuntos a cada lado de un símbolo de relación, entonces\(=\),\(⊆\) y\(⊇\) son símbolos de relación válidos. Si pensamos en colocar expresiones lógicas a ambos lados de una relación entonces, honestamente, cualquiera de los símbolos lógicos es una relación, pero normalmente pensamos en\(∧\) y\(∨\) como operadores y damos cosas como\(≡\),\(\implies\) y\(\iff\) el estado de las relaciones.
En los ejemplos que hemos visto las cosas a cada lado de una relación son del mismo tipo. Esto suele ser, pero no siempre, el caso. La prevalencia de relaciones con el mismo tipo de cosas que se comparan ha llevado incluso al aforismo “No compare manzanas y naranjas”. Piensa en el símbolo\(∈\) por un momento. Como hemos visto anteriormente, no suele ser apropiado poner conjuntos a ambos lados de este, podríamos tener números u otros objetos a la izquierda y conjuntos a la derecha. Veamos un pequeño ejemplo. Dejar\(A = \{1, 2, 3, a, b\}\) y dejar\(B = \{\{1, 2, a\}, \{1, 3, 5, 7, . . .\}, \{1\}\}\). El “elemento de” relación,\(∈\), es una relación de\(A\) a\(B\).
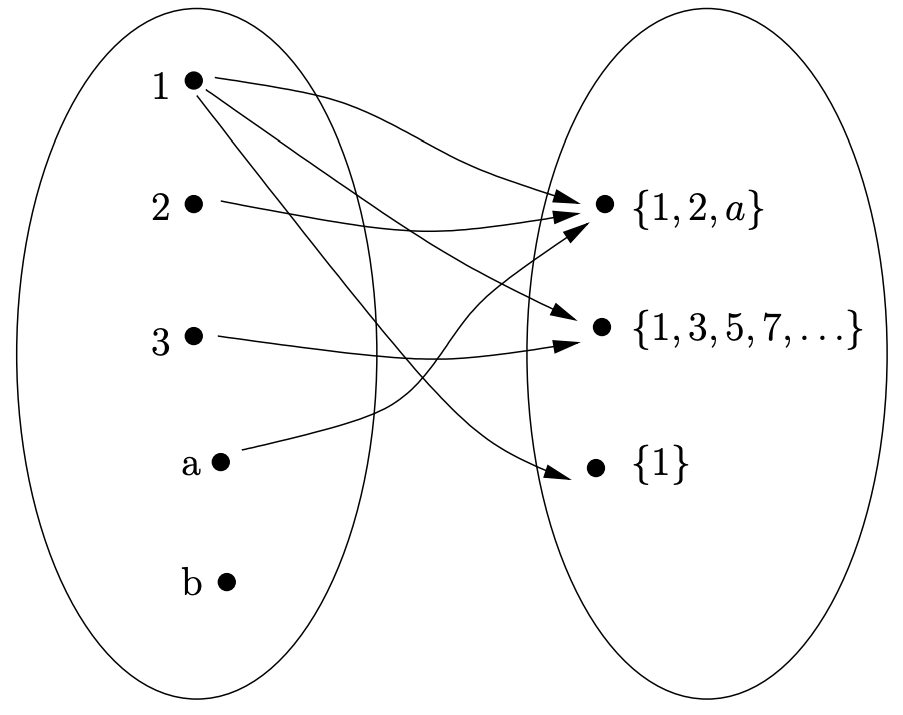
Un diagrama como el que hemos dado en Figura\(6.1.1\) parece algo muy natural. Tales imágenes ciertamente nos dan una herramienta visual fácil para pensar en las relaciones. Pero debemos señalar ciertas suposiciones ocultas. Primero, solo funcionarán si estamos tratando con conjuntos finitos, o conjuntos como los números impares en nuestro ejemplo (conjuntos que son infinitos pero que en principio podrían enumerarse). Segundo, al dibujar los dos conjuntos por separado, parece que estamos asumiendo que no sólo son diferentes, sino disjuntos. Los sets no solo no necesitan ser disjuntos, sino a menudo (¡la mayoría de las veces!) tenemos relaciones que van de un conjunto a sí mismo así que los sets en una imagen como esta pueden ser idénticos. En Figura\(6.1.2\) ilustramos la relación de divisibilidad en el conjunto de todos los divisores de\(6\) — este es un ejemplo en el que los conjuntos a cada lado de la relación son los mismos. Observe la distinción lingüística, podemos hablar ya sea de “una relación de\(A\) a\(B\)” (cuando realmente hay dos conjuntos diferentes) o de “una relación sobre\(A\)” (cuando solo hay uno).
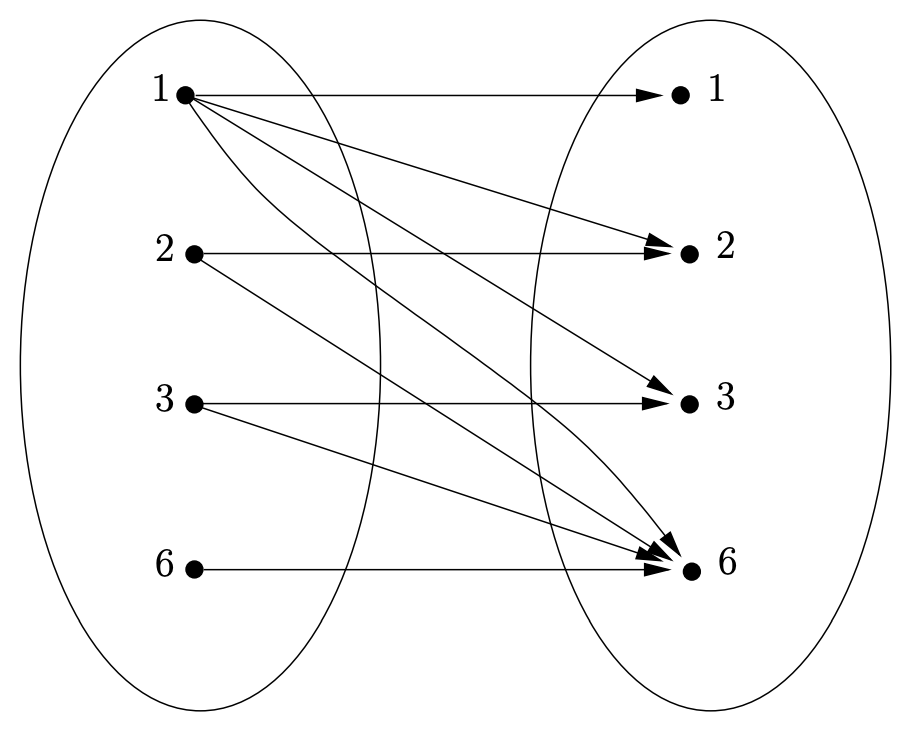
Los puristas notarán que es realmente inapropiado representar el mismo conjunto en dos lugares diferentes en un diagrama de Venn. El diagrama en la Figura realmente\(6.1.2\) debería verse así:
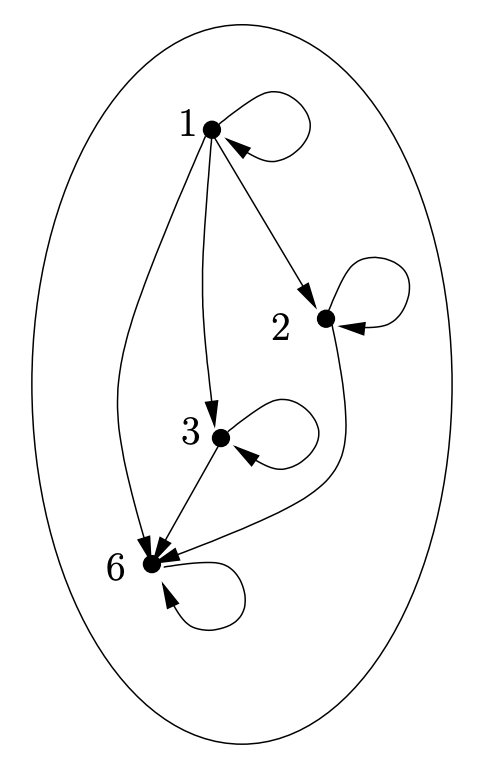
En efecto, esta representación es definitivamente preferible, aunque puede estar más concurrida. Una imagen como esta se conoce como la gráfica dirigida (también conocida como dígrafo) de la relación.
Recordemos que cuando estábamos discutiendo conjuntos dijimos que la mejor manera de describir un conjunto es simplemente enumerar todos sus elementos. Bueno, ¿cuál es la mejor manera de describir una relación? En el mismo espíritu, parecería que deberíamos enumerar explícitamente todas las cosas que hacen cierta la relación. Pero se necesitan un par de cosas, una para ir por el lado izquierdo y otra para ir por la derecha, para hacer una relación verdadera (¡o para el caso falsa!). Además, debe ser evidente que el orden es importante en este contexto, por ejemplo\(2 < 3\) es cierto pero\(3 < 2\) no lo es La identidad de una relación está tan íntimamente ligada al conjunto de pares ordenados que la hacen cierta, que al tratar relaciones abstractas las definimos como conjuntos de ordenadas pares.
Dado dos conjuntos,\(A\) y\(B\), el producto cartesiano de\(A\) y\(B\) es el conjunto de todos los pares ordenados\((a, b)\) donde\(a\) está en\(A\) y\(b\) está en\(B\). Denotamos el producto cartesiano usando el símbolo\(×\).
\(A × B = \{(a, b) a ∈ A ∧ b ∈ B\}\)
De aquí en adelante en tu carrera matemática, deberás tomar nota del contexto en el que\(×\) aparece el símbolo. Si aparece entre números sigue adelante y multiplica, pero si aparece entre conjuntos estás haciendo algo diferente —formando el producto cartesiano.
El familiar\(x\) —\(y\) plano, a menudo se llama el plano cartesiano. Esto se hace por dos razones. René Descartes, el famoso matemático y filósofo, fue el primero en considerar la coordinación del plano y así es responsable de nuestra comprensión actual de la relación entre geometría y álgebra. El nombre de René Descartes también se memoriza en la definición del producto cartesiano de conjuntos, y el plano no es más que el producto\(\mathbb{R} × \mathbb{R}\). En efecto, el plano proporcionó el primer ejemplo del concepto que posteriormente se generalizó al producto cartesiano de conjuntos.
Supongamos\(A = \{1, 2, 3\}\) y\(B = \{a, b, c\}\). ¿Está\((a, 1)\) en el producto cartesiano\(A × B\)? Listar todos los elementos de\(A × B\).
En resumen, podemos definir una relación como cualquier subconjunto de un producto cartesiano apropiado. Entonces, una relación abstracta\(\text{R}\) de un conjunto\(A\) a un conjunto\(B\) es solo un subconjunto de A×B. similar, una relación\(\text{R}\) en un conjunto\(S\) se define por un subconjunto de\(S × S\). Esta definición se ve un poco extraña cuando la aplicamos a una relación real (concreta) que ya conocemos. Considera la relación “menor que”. Para describir “menos que” como un subconjunto de un producto cartesiano debemos escribir
\(< = \{(x, y) ∈ \mathbb{R} × \mathbb{R} y − x ∈ \mathbb{R}^+\}\).
Esto se ve gracioso.
También, si hemos definido alguna relación\(\text{R} ⊆ A × B\), entonces para decir que un par particular,\((a, b)\), de las cosas hacen verdadera la relación tenemos que escribir
\(a\text{R}b\).
Esto también se ve gracioso.
A pesar de las extrañas apariencias, estos ejemplos sí expresan la forma correcta de lidiar con las relaciones.
Hagamos un ejemplo completamente maquillado. Supongamos que\(A\) es el conjunto\(\{a, e, i, o, u\}\) y\(B\) es el conjunto\(\{r, s, t, l, n\}\) y definimos una relación de\(A\) a\(B\) por
\(R = \{(a, s),(a, t),(a, n),(e, t),(e, l),(e, n),(i, s),(i, t),(o, r),(o, n),(u, s)\}\).
Entonces, por ejemplo, porque\((e, t) ∈ \text{R}\) podemos escribir\(e\text{R}t\). Indicamos la negación del concepto de que dos elementos están relacionados dibujando un slash a través del nombre de la relación, por ejemplo la notación\(\neq\) es ciertamente familiar para usted, tal como es\(\nless\) (aunque en este último caso normalmente escribiríamos en\(≥\) su lugar). Podemos denotar el hecho de que no\((a, l)\) es un par que haga verdadera la relación por escrito\(a \not \text{R} l\).
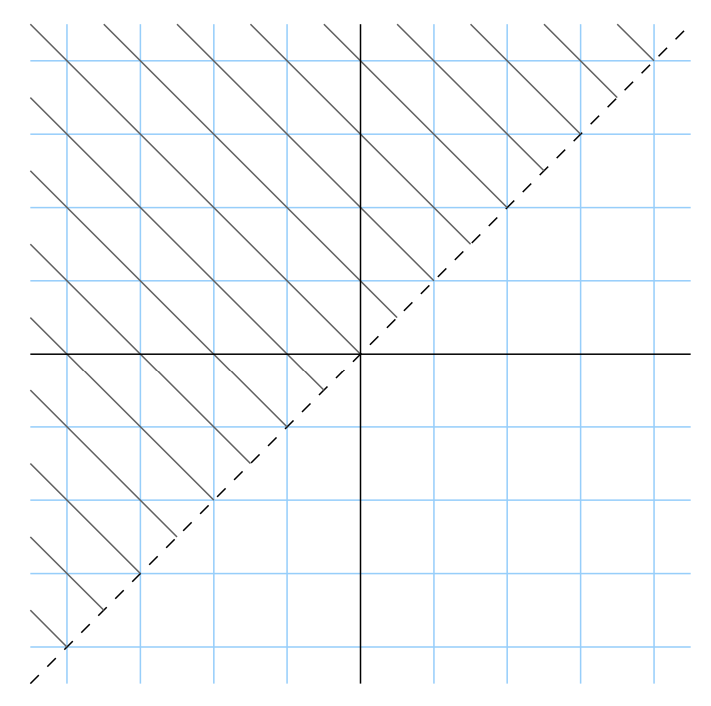
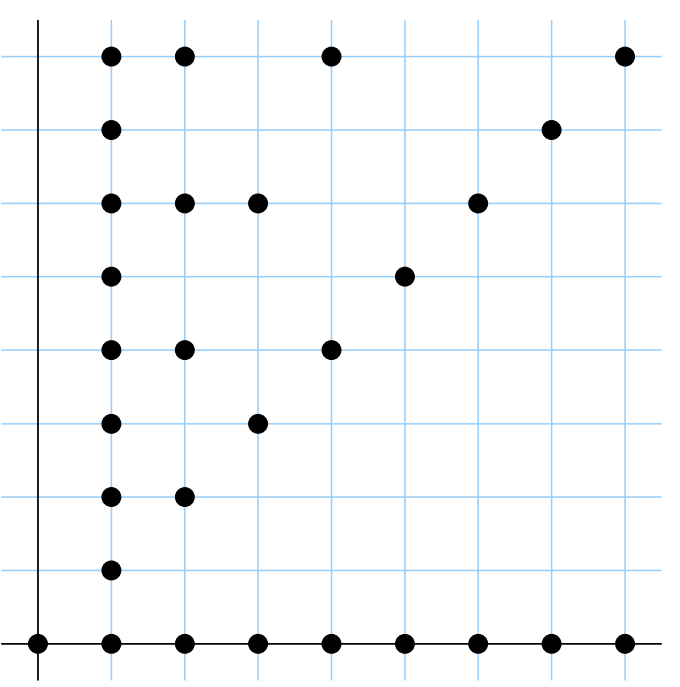
Habría que mencionar otra forma de visualizar las relaciones. Cuando estamos tratando con una relación en\(\mathbb{R}\), la relación es en realidad un subconjunto de\(\mathbb{R} × \mathbb{R}\), eso significa que podemos ver la relación como un subconjunto del\(y\) plano\(x\) —. En otras palabras, podemos graficarlo. La gráfica de la relación “\(<\)” se da en la Figura\(6.1.3\).
También se\(\mathbb{R}\) puede graficar una relación en cualquier conjunto que sea un subconjunto de. La gráfica de la relación “\(|\)” se da en la Figura\(6.1.4\).
Eventualmente, nos pondremos en torno a definir funciones como relaciones que tienen cierta propiedad agradable. Por el momento, solo notaremos que algunas de las operaciones a las que estás acostumbrado a usar con funciones también se aplican con las relaciones. Cuando una función “deshace” lo que otra función “hace” decimos que las funciones son inversas. Por ejemplo, la función\(f(x) = 2x\) (es decir, duplicar) y la función\(g(x) = \dfrac{x}{2}\) (halving) son funciones inversas porque, no importa con qué número comencemos, si la doblamos y luego dividimos a la mitad ese resultado, terminamos con el número original. Se escribe el inverso de una relación\(\text{R}\)\(\text{R}^{−1}\) y consiste en las inversiones de los pares en\(\text{R}\),
\(\text{R}^{−1} = \{(b, a) (a, b) ∈ \text{R}\}\).
Esto también se puede expresar por escrito
\(b\text{R}^{−1}a \iff a\text{R}b.\)
El proceso de “hacer una función y luego hacer otra” se conoce como composición funcional. Por ejemplo, si\(f(x) = 2x + 1\) y\(g(x) = \sqrt{x}\), entonces podemos componerlos (en dos órdenes diferentes) para obtener cualquiera\(f(g(x)) = 2 \sqrt{x} + 1\) o\(g(f(x)) = \sqrt{2x + 1}\). Al componer funciones hay un “resultado intermedio” que obtienes aplicando la primera función a tu entrada, y luego calculas el valor de la segunda función en el resultado intermedio. (Por ejemplo, en el cálculo\(g(f(4))\) obtenemos el resultado intermedio\(f(4) = 9\) y luego pasamos a calcular\(g(9) = 3\).)
La definición del compuesto de dos relaciones se centra mucho en esta idea del resultado intermedio. Supongamos que\(\text{R}\) es una relación de\(A\) a\(B\) y\(\text{S}\) es una relación de\(B\) a\(C\) entonces el compuesto\(\text{S} ◦ \text{R}\) viene dado por
\(\text{S} ◦ \text{R} = \{(a, c) ∃b ∈ B,(a, b) ∈ \text{R} ∧ (b, c) ∈ \text{S}\}\).
En esta definición,\(b\) está el “resultado intermedio”, si no existe tal b que sirva\(a\) para conectarse\(c\) entonces\((a, c)\) no estará en el compuesto. Además, fíjate que esta es la composición\(\text{R}\) primero\(\text{S}\), luego, pero está escrita como\(\text{S} ◦ \text{R}\) — ¡cuidado con esto! Las composiciones de las relaciones deben leerse de derecha a izquierda. Esta convención tiene sentido cuando se considera la composición funcional,\(f(g(x))\) significa\(g\) primero, entonces\(f\) entonces si usamos la notación de “pequeño círculo” para la composición de las relaciones\(f ◦g(x) = f(g(x))\) que tenemos lo cual es agradable porque los símbolos\(f\) y\(g\) aparecen en el mismo orden. ¡Pero ten cuidado! hay atavistas por ahí que escriben sus composiciones al revés.
Probablemente deberías tener en mente un diagrama como el siguiente mientras piensas en la composición de las relaciones. Aquí, tenemos el set\(A = \{1, 2, 3, 4\}\), el conjunto\(B\) es\(\{a, b, c, d\}\) y\(C = \{w, x, y, z\}\). La relación\(\text{R}\) va de\(A\) a\(B\) y consiste en el siguiente conjunto de pares,
\(R = \{(1, a),(1, c),(2, d),(3, c),(3, d)\}\).
Y
\(S = \{(a, y),(b, w),(b, x),(b, z)\}\).
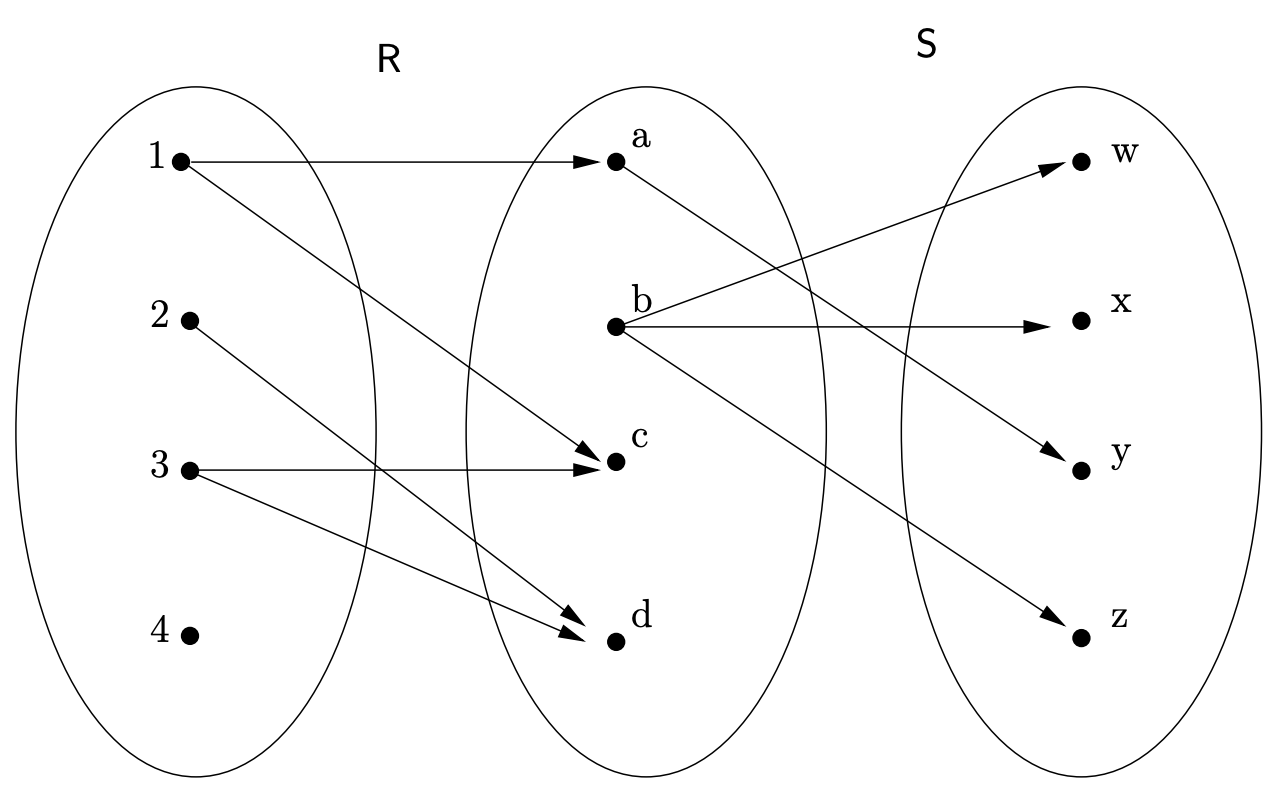
Observe que la composición\(\text{R} ◦ \text{S}\) es imposible (o, más propiamente, está vacía). ¿Por qué? ¿Cuál es el (único) par en la composición\(\text{S} ◦ \text{R}\)?
Ejercicios:
El orden lexicográfico,\(<_{\text{lex}}\), es una relación en el conjunto de todas las palabras, donde\(x <_{\text{lex}} y\) significa que\(x\) vendría antes\(y\) en el diccionario. Considera solo las palabras de tres letras como “iff”, “higo”, “la”, etcétera. Cree una definición utilizable para\(x_1x_2x_3 <_{\text{lex}} y_1y_2y_3\).
¿Cuál es la gráfica de “\(=\)” en\(\mathbb{R} × \mathbb{R}\)?
Se denota la inversa\(\text{R}\) de una relación\(\text{R}^{−1}\). Contiene exactamente los mismos pares ordenados que\(\text{R}\) pero con la orden conmutada. (Entonces, técnicamente, no son exactamente los mismos pares ordenados.)
\(\text{R}^{−1} = \{(b, a) (a, b) ∈ \text{R}\}\)
Definir una relación\(\text{S}\) sobre\(\mathbb{R} × \mathbb{R}\) por\(\text{S} = \{(x, y) y = \sin x\}\). ¿Qué es\(\text{S}^{−1}\)? Dibuja una sola gráfica que contenga\(\text{S}\) y\(\text{S}^{−1}\).
La regla de los “calcetines y zapatos” es una pequeña mnemotécnica muy tonta para recordar cómo invertir una composición. Si pensamos en deshacer el proceso de ponernos los calcetines y los zapatos (eso son los calcetines primero, luego los zapatos) primero tenemos que quitarnos los zapatos, luego quitarnos los calcetines.
La regla de calcetines y zapatos también es válida para las relaciones.
\((\text{S} ◦ \text{R})^{−1} = \text{R}^{−1} ◦ \text{S}^{−1}\)Demuéstralo.