1.2: El primer álgebra y la primera interpretación
( \newcommand{\kernel}{\mathrm{null}\,}\)
Antes de hablar de álgebra, uno debe en principio saber qué se entiende por esa palabra. Por el momento, sin embargo, dejaremos de lado esta cuestión; volveremos a ella al final del libro; todo lo que necesitamos saber por el momento es que el álgebra tiene que ver con ecuaciones.

En efecto, cuando los historiadores de las matemáticas descubrieron a finales de la década de 1920 que ciertos textos cuneiformes (véase el recuadro “Escritura cuneiforme”, página 10) contienen problemas “algebraicos”, creían que todos conocían el significado de la palabra.
Aceptémoslo para entrar en su pensamiento, y veamos un ejemplo muy sencillo extraído de un texto escrito durante el siglo XVIII a. C. en la transliteración normalmente utilizada por los asiriólogos, en cuanto a la función de cursiva y minúsculas, véase la página 23 y la casilla “Escritura cuneiforme, ” página 10 (La figura 1.1 muestra la versión cuneiforme del texto):
1 a.šà l [am] ù mi-it-ar-ti ak-m [ur-m] a 45-e 1 wa-ṣi-tam
2 ta-ša-ka-an ba-ma-at 1 te-e-pe [3] 0 ù 30 tu-uš-ta-kal
3 15 a-na 45 tu-ṣa-ab-ma 1- [e] 1 íb.si 8 30 ša tu-uš-ta-ki-lu
4 lìb-ba 1 ta-na-sà-a-ma 30 mi-it-ar-tum
El lector desprevenido, al encontrar esto complicado, debería saber que para los pioneros era casi igual de complicado. Ochenta años después entendemos la terminología técnica de los textos matemáticos babilónicos antiguos; pero en 1928 aún no se había descifrado, y los números contenidos en los textos tenían que proporcionar el punto de partida. 1
Escritura Cuneiforme
Desde su primer inicio, la escritura mesopotámica se realizó sobre una pieza aplanada de arcilla, que luego se secó al aire después de la inscripción (una “tablilla”). En el cuarto milenio, los signos eran dibujos realizados por medio de un lápiz puntiagudo, en su mayoría dibujos de objetos reconocibles que representaban conceptos simples. Los conceptos complejos se podían expresar a través de la combinación de los signos; una cabeza y un tazón que contenían la ración diaria de un trabajador significaban “asignación de grano” (y posteriormente “para comer”).
Los signos para números y medidas, sin embargo, fueron hechos por impresión vertical u oblicua de un lápiz cilíndrico.
Con el tiempo, el carácter del guión cambió de dos maneras. En primer lugar, en lugar de trazar señales consistentes en líneas curvas, uno los impresionó con un lápiz con bordes afilados, disolviendo las líneas curvas en una secuencia de segmentos rectos. De esta manera, los signos parecen estar compuestos por pequeñas cuñas (de ahí el nombre “cuneiforme”).
En la segunda mitad del tercer milenio, los signos numéricos y metrológicos llegaron a escribirse de la misma manera. Los signos se volvieron cada vez más estilizados, perdiendo su calidad pictográfica; entonces no es posible adivinar el dibujo subyacente a menos que se conozca el desarrollo histórico detrás del letrero. Hasta alrededor del 2000 a. C., sin embargo, las variaciones de personajes de un escriba a otro muestran que los escribas conocían los dibujos originales.
Veamos, por ejemplo, el personaje que inicialmente representaba un jarrón con un pico (izquierda).
En el medio vemos tres variantes del tercer milenio del mismo personaje (debido a que el guión se giró 90 grados a la izquierda en el segundo milenio, es habitual mostrar el guión del tercer milenio de la misma manera). Si conoces el origen, aún es fácil reconocer la imagen subyacente. A la derecha vemos dos variantes babilónicas antiguas; aquí ya no se sugiere la imagen.
El otro cambio se refiere al uso de la forma en que se utilizaron los signos (lo que implica que mejor deberíamos hablar de ellos como “personajes”). Se excava la palabra sumeria para el jarrón. A medida que diversos géneros literarios se desarrollaban junto a la contabilidad (por ejemplo, inscripciones reales, contratos y colecciones de proverbios), los escribas necesitaban formas de escribir sílabas que sirvieran para indicar declinaciones gramaticales o sustantivos propios. Este sistema silábico sirvió también en la escritura de acadio. Para ello, se utilizaron signos según su valor fonético aproximado; el “jarrón” puede representar así las sílabas cavadas, duk, remolcador y tuk. En la escritura babilónica, el signo sumerio también podría servir como un “logograma” o “signo de palabra” para una palabra que significa lo mismo que cavado, es decir, karpatum
Las palabras que deben leerse como logogramas o en sumerio se transliteran en minúsculas; los especialistas (cf. Apéndice B) a menudo distinguen las palabras sumerias cuyo valor fonético se supone que debe conocerse, las cuales luego se escriben en s p a c e d w r i t i n g, de las renderizadas por su “nombre de signo” (correspondiente a posible lectura), que se escriben como pequeñas mayúsculas. La escritura fonética acadio se transcribe en cursiva.
Los asiriólogos distinguen “transcripciones” de “transliteraciones”. Una “transcripción” es una traducción intencionada al acadio escrita en alfabeto latino. En una “transliteración” cada carácter cuneiforme se renderiza por separado según su supuesto valor fonético o logográfico.
Ya se sabía que estos números estaban escritos en un sistema de valor posicional con base 60 pero sin indicación de orden absoluto de magnitud (véase el recuadro “El Sistema Sexagesimal”, página 14). Debemos suponer que los números que aparecen en el texto están conectados, y que son de al menos aproximadamente el mismo orden de magnitud (recordamos que “1” puede significar uno así como 60 o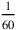 ). Por lo tanto, intentemos interpretar estos números en el siguiente orden:
). Por lo tanto, intentemos interpretar estos números en el siguiente orden:
45′(=34)−1∘−1∘−30′(=12)−30′−15′(=14)−45′−1∘−1∘−30′−1∘−30′.
Para dar el siguiente paso se necesita algo de fantasía. Notando que30′ es12⋅1 y15′=(30′)2 podemos pensar en la ecuación
x2+1⋅x=34.
Hoy lo resolvemos en estos pasos (descuidando números negativos, una invención moderna):
\ begin {alineado}
x^ {2} +1\ cdot x=\ frac {3} {4} &\ Leftrightarrow x^ {2} +1\ cdot x+\ izquierda (\ frac {1} {2}\ derecha) ^ {2} =\ frac {3} {4} +\ izquierda (\ frac {1} {2}\ derecha) ^ {2}
\\ Izquierda y x^ {2} +1\ cdot x+\ izquierda (\ frac {1} {2}\ derecha) ^ {2} =\ frac {3} {4} +\ frac {1} {4} =1\\
&\ Izquierda fila\ izquierda (x+\ frac {1} {2}\ derecha) ^ {2} =1\\
\ Izquierda y x+\ frac {1} {2} =\ sqrt {1} =1\\\ Izquierda y x=1-
\ frac {1} {2} =\ frac {1} {2} =\ frac {1} {2}
\ final {alineado}.
Como vemos, el método se basa en la suma, a ambos lados de la ecuación, del cuadrado sobre la mitad del coeficiente del término de primer grado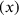 —aquí
—aquí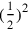 . Eso nos permite reescribir el lado izquierdo como el cuadrado en un binomio:
. Eso nos permite reescribir el lado izquierdo como el cuadrado en un binomio:
x2+1⋅x+(12)2=x2+2⋅12⋅x+(12)2=(x+12)2.
Este pequeño truco se llama una “finalización cuadrática”.
Comparando el texto antiguo y la solución moderna notamos que los mismos números ocurren casi en el mismo orden. Lo mismo vale para muchos otros textos. A principios de la década de 1930 los historiadores de las matemáticas se convencieron de que entre 1800 y 1600 a. C. los escribas babilónicos sabían algo muy similar a nuestra álgebra de ecuaciones. Este periodo constituye la segunda mitad de lo que se conoce como la época “Babilónica antigua” (véase el recuadro “Rudimentos de la Historia General”, página 7).
El siguiente paso fue interpretar los textos con precisión. Hasta cierto punto, el significado general, no técnico, del vocabulario podría ayudar. En la línea 1 del problema de la página 9, ak-mur puede traducirse “He colmado”. Una comprensión del “amontonamiento” de dos números como una adición parece natural y concuerda con la observación de que el “amontonamiento” de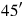 y
y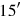 (es decir, de
(es decir, de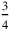 y
y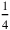 ) produce 1. Cuando otros textos “elevan” (našûm) una magnitud a otra, se vuelve más difícil. Sin embargo, se puede observar que el “aumento” de 3 a 4 produce 12, mientras que 5 “elevado” a 6 rinde 30, y con ello adivinar que “subir” es una multiplicación.
) produce 1. Cuando otros textos “elevan” (našûm) una magnitud a otra, se vuelve más difícil. Sin embargo, se puede observar que el “aumento” de 3 a 4 produce 12, mientras que 5 “elevado” a 6 rinde 30, y con ello adivinar que “subir” es una multiplicación.
De esta manera, los estudiosos de la década de 1930 llegaron a elegir una interpretación puramente aritmética de las operaciones, es decir, como sumas, restas, multiplicaciones y divisiones de números. Esta traducción ofrece un ejemplo: 2
1 He añadido la superficie y (el lado de) mi cuadrado:45′.
2 Usted postula1∘, la unidad. Se rompe en dos1∘:30′. Multiplica (entre sí)[30′]and30r:
315′. Te unes15′ a45′:1∘. 1∘es el cuadrado de1∘. 30′, que has multiplicado (por sí mismo),
4 de1∘ ti restar:30′ es el (lado del) cuadrado.
Tales traducciones aún se encuentran hoy en día en las historias generales de las matemáticas. Explican los números que aparecen en los textos, y dan una impresión casi moderna de los antiguos métodos babilónicos. No hay diferencia fundamental entre la traducción anterior y la solución por medio de ecuaciones. Si el lado de la plaza esx, entonces su área esx2. Por lo tanto, la primera línea del texto —el problema a resolver— corresponde a la ecuaciónx2+1⋅x=34. Continuando con la lectura de la traducción vemos que sigue las transformaciones simbólicas en la página 12 paso a paso.
Sin embargo, aunque la presente traducción así como otras realizadas según los mismos principios explican los números de los textos, coinciden menos con sus palabras, y a veces no con el orden de las operaciones. En primer lugar, estas traducciones no toman en cuenta el carácter geométrico de la terminología, suponiendo que palabras y expresiones como “(el lado de) mi cuadrado”, “largo”, “ancho” y “área” de un rectángulo denotan nada más que números desconocidos y sus productos. Hay que reconocer que en la década de 1930 eso no parecía imposible a priori —nosotros también hablamos32 como el “cuadrado de 3" sin pensar en un cuadrilátero.
Pero hay otros problemas. El más severo es probablemente que el número de operaciones es demasiado grande. Por ejemplo, hay dos operaciones que en la interpretación tradicional se entienden como adición: “unirse a” (waṣābum /da [+.1ex] h, el infinitivo correspondiente al tu-ṣa-ab de nuestro texto) y “a montón” (kamārum /gar.gar, a partir de las cuales el ak-mur del texto). Ambas operaciones se encuentran así en nuestro breve texto, “apilando” en la línea 1 (donde aparece como “agregar”) y “unir” en la línea 3.
El Sistema Sexagesimal de Plaze-Valor
Los textos matemáticos babilónicos antiguos hacen uso de un sistema numérico de valor posicional60 con base sin indicación de un “punto sexagesimal”. Dentro de la notación, que también emplea el valor posicional, el dígito1 "" ciertamente puede representar el número1, pero también los números10100...,,, así como0.1,0.01,.... Su valor está determinado por su distancia desde el punto decimal.
Del mismo modo,45 "" escrito por un escriba babilónico puede significar45; pero también puede significar4560 (así34); para45⋅60; etc. Ningún punto decimal determina su valor “verdadero”. El sistema corresponde a la regla de cálculo de la cual los ingenieros hicieron uso antes de la llegada de la calculadora electrónica de bolsillo. Este dispositivo tampoco tenía punto decimal, y por lo tanto no indicaba el orden absoluto de magnitud. Para saber si una construcción específica pediría3.5m3,35m3 o350m3 de concreto, el ingeniero recurrió al cálculo mental.
Para escribir números entre 1 y 59, los babilonios hicieron uso de una cuña vertical (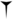 ) repetida hasta 9 veces en patrones fijos para los números del 1 al 9, y de un Winkelhaken (una palabra prestada alemana que originalmente significa “gancho angular”) (
) repetida hasta 9 veces en patrones fijos para los números del 1 al 9, y de un Winkelhaken (una palabra prestada alemana que originalmente significa “gancho angular”) ( ) repetida hasta 5 veces para los números 10,20,...,50.
) repetida hasta 5 veces para los números 10,20,...,50.
Un lector moderno no está acostumbrado a leer números con un orden de magnitud indeterminado. En las traducciones de textos matemáticos babilónicos es por lo tanto costumbre indicar el orden de magnitud que se tiene que atribuir a los números. Varios métodos para hacer eso están en uso. En el presente trabajo emplearemos una generalización de la notación grado-minuto-segundo. Si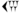 significa1560, lo transcribiremos15′, si corresponde1560⋅60, escribiremos15′′. Si representa15⋅60, escribimos
significa1560, lo transcribiremos15′, si corresponde1560⋅60, escribiremos15′′. Si representa15⋅60, escribimos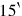 , etc. si representa15, escribimos15 o, si eso es necesario para evitar malentendidos,15∘.
, etc. si representa15, escribimos15 o, si eso es necesario para evitar malentendidos,15∘. 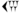 entendido como así10+5⋅60−1 será transcrito10∘5′
entendido como así10+5⋅60−1 será transcrito10∘5′
 entendido como30′ así significa12.
entendido como30′ así significa12.
 entendidos como45′ medios34.
entendidos como45′ medios34.
 entendido como12′ medio15; entendido como
entendido como12′ medio15; entendido como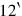 significa720.
significa720.
 entendidos como10′ medios16.
entendidos como10′ medios16.
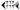 puede significar
puede significar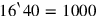 o16∘40′=1623, etc.
o16∘40′=1623, etc.
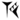 puede significar
puede significar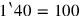 1∘40′=123,1′40′′=136,, etc.
1∘40′=123,1′40′′=136,, etc.
Fuera de la escuela, los babilonios emplearon el sistema de valor posicional exclusivamente para cálculos intermedios (exactamente como un ingeniero utilizó la regla de cálculo hace cincuenta años). Cuando un resultado iba a insertarse en un contrato o en una cuenta, obviamente no podían permitirse ser ambiguos; otras anotaciones les permitían expresar el número precisse que
pretendido.
Ciertamente, nosotros también sabemos de sinónimos incluso dentro de las matemáticas, por ejemplo, “y”, “sumado a” y “más”; la elección de una palabra u otra depende del estilo, de los hábitos personales, de nuestras expectativas con respecto al interlocutor, etc. Thureau-Dangin, como vemos, hace uso de ellos, siguiendo las distinciones del texto hablando primero de “adición” y segundo de “unión”; pero sostiene que no hay diferencia conceptual, y que nada más que sinónimos están involucrados, “solo hay una multiplicación”, como explica sin notando que el argumento es circular.
Sinónimos, es cierto, también se pueden encontrar en las matemáticas babilónicas antiguas. Así, los verbos “arrancar” (nasāum /zi) y “cortar” (arāṣum /kud) son nombres para la misma operación sustractiva: pueden ser utilizados en situaciones estrictamente análogas. La diferencia entre “unir” y “colmar”, sin embargo, es de otro tipo. No existe ningún texto que se refiera a una terminación cuadrática (arriba, página 12) como un “apilamiento”. “Amonar”, por otro lado, es la operación que se utilizará cuando se agrega un área y una extensión lineal. Por lo tanto, se trata de operaciones distintas, no de dos nombres diferentes para una misma operación. De la misma manera, hay dos “sustracciones” distintas, cuatro “multiplicaciones” e incluso dos “mitades” diferentes. Volveremos a esto.
Una traducción que mezcla operaciones que los babilonios trataron como distintas puede explicar por qué los cálculos babilónicos conducen a resultados correctos; pero no puede penetrar en su pensamiento matemático.
Además, las traducciones tradicionales tuvieron que saltarse ciertas palabras que parecían no tener sentido. Por ejemplo, una traducción más literal de la última línea de nuestro pequeño problema comenzaría “desde el interior de1∘" (o incluso “desde el corazón” o “desde los intestinos”). Al no ver cómo un número 1 podía poseer un “interior” o “entrañas”, los traductores descartaron tácitamente la palabra.
Otras palabras fueron traducidas de una manera que difiere tan fuertemente de su significado normal que debe despertar sospechas. Normalmente, la palabra traducida “unidad” por Thureau-Dangin y “coeficiente” por Neugebauer (waṣītum, de waṣûm, “salir”) se refiere a algo que sobresale, como esa parte de un edificio de la que los arquitectos hablan como una “proyección”. Eso debió parecer absurdo, ¿cómo puede “destacarse” un número 1? Por lo tanto los traductores prefirieron hacer que la palabra correspondiera a algo conocido en las matemáticas de sus propios días.
Por último, el orden en que se realizan las operaciones a veces es diferente de lo que parece natural en la lectura aritmética.
A pesar de estas objeciones, la interpretación que resultó en la década de 1930 fue un logro impresionante, y sigue siendo una excelente “primera aproximación”. Los estudiosos que la produjeron no fingieron nada más. Otros sin embargo, no menos importantes historiadores de las matemáticas y matemáticos históricamente interesados, lo tomaron como el desciframiento único y final del “álgebra babilónica” —tan impresionantes fueron los resultados que se obtuvieron, y tan aterradora la perspectiva de verse obligados a leer los textos en su idioma original. Hasta la década de 1980, nadie notó que ciertos sinónimos aparentes representan operaciones distintas. 3


