Saltar al contenido principal
LibreTexts Español

4.5: Funciones de Valor Absoluto

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112521

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Para graficar las funciones de valor absoluto, elija valores pequeños de\(x\), y calcule el valor\(f(x)\) de de la función dada para crear pares ordenados. Tres pares ordenados es la cantidad mínima necesaria para graficar una función de valor absoluto. Tenga cuidado, porque un par ordenado debe representar el vértice, el punto donde se encuentran los lados izquierdo y derecho de la función. Para graficar correctamente la forma de la función de valor absoluto, se debe encontrar el vértice.

    \(f(x) = a\vert x − h\vert+ k\)Forma general de una función de valor absoluto, con vértice\((h,k)\)

    • \(a\)determina tanto el ancho como la orientación (hacia arriba o hacia abajo) de la función.
    • \(h\)es el desplazamiento horizontal desde el origen.
    • \(k\)es el desplazamiento vertical desde el origen.

    Comienza identificando el par ordenado del vértice, y luego encuentra un par ordenado a la izquierda del origen, y a la derecha del origen. Elija un valor x una unidad a la izquierda del valor x del origen, calcule\(f(x)\) y luego elija un valor x una unidad a la derecha del valor x del origen y calcule\(f(x)\). La gráfica se asemejará a una\(V\), ya sea orientada hacia arriba o hacia abajo, dependiendo del signo de\(a\).

    Ejemplo 4.5.1

    Cree una tabla de soluciones y grafique la siguiente función de valor absoluto:

    \(f(x) = \vert x − 4\vert\)

    Solución

    Comparando esta función con la forma general para las funciones de valor absoluto (mostradas arriba),\(a = 1\),\(h = 4\),\(k = 0\). El vértice es\((h, k)\) o\((4, 0)\).

    Para encontrar dos pares más ordenados, elija\(x = 3\) y\(x = 5\), luego calcule los valores de\(f(x)\).

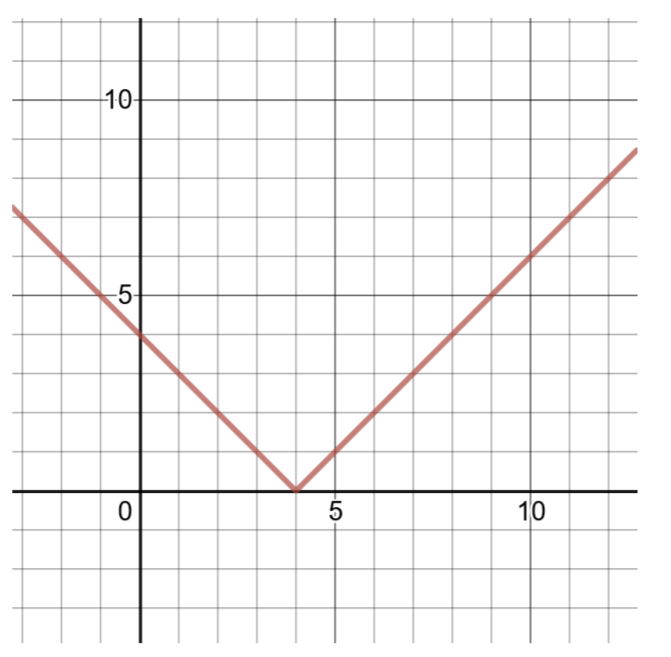
    clipboard_e4c9bfc2e550aa369ba89481f9ab5d4fb.png
    Figura 4.5.1
    Tabla de soluciones para\(f(x) = \vert x − 4\vert\)
    \(x\) \(f(x)\)
    \ (x\) ">3 \ (f (x)\) ">\(f(3) = \vert 3 − 4\vert = \vert − 1\vert = 1\)
    \ (x\) ">4 \ (f (x)\) ">\(f(4) = \vert 4 − 4\vert = \vert 0\vert = 0\)
    \ (x\) ">5 \ (f (x)\) ">\(f(5) = \vert 5 − 4\vert = \vert 1\vert = 1\)
    Ejemplo 4.5.2

    Cree una tabla de soluciones y grafique la siguiente función de valor absoluto:

    \(g(x) = \vert x + 2\vert − 5\)

    Solución

    Comparando esta función con la forma general para las funciones de valor absoluto (mostradas arriba),\(a = 1\),\(h = −2\),\(k = −5\). El vértice es (h, k)\) o\((−2, −5)\).

    Para encontrar dos pares más ordenados, elija\(x = −3\) y\(x = −1\), luego calcule los valores de\(g(x)\)

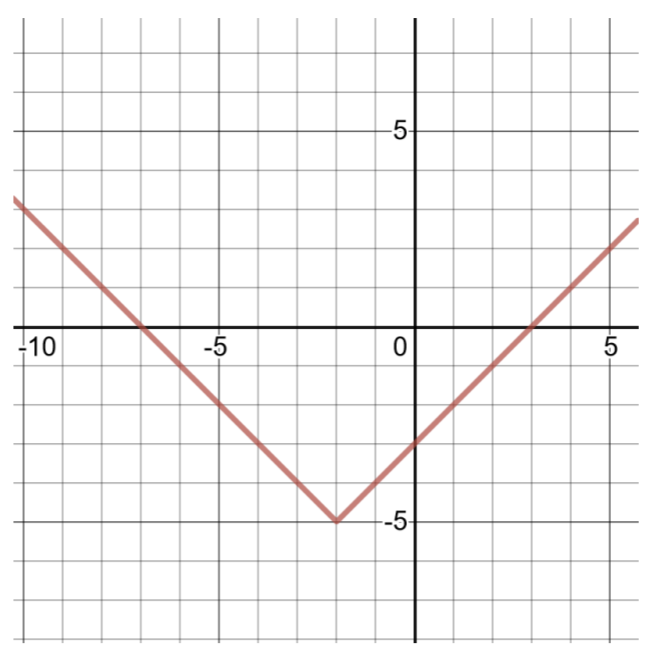
    clipboard_e4ca56e46ab74be7e1b0eaaea223f1a1d.png
    Figura 4.5.2
    Tabla de soluciones para\(g(x) = \vert x + 2\vert − 5\)
    \(x\) \(g(x)\)
    -3 \(g(−3) = \vert − 3 + 2\vert − 5 = \vert − 1\vert − 5 = 1 − 5 = −4\)
    -2 \(g(−2) = \vert − 2 + 2\vert − 5 = \vert 0\vert − 5 = 0 − 5 = −5\)
    -1 \(g(−1) = \vert − 1 + 2\vert − 5 = \vert 1\vert − 5 = 1 − 5 = −4\)
    Ejemplo 4.5.3

    Cree una tabla de soluciones y grafique la siguiente función de valor absoluto:

    \(h(x) = 3\vert x − 5\vert + 1\)

    Solución

    Comparando esta función con la forma general para las funciones de valor absoluto (mostradas arriba),\(a = 3\),\(h = 5\),\(k = 1\). El vértice es\((h, k)\) o\((5, 1)\).

    Para encontrar dos pares más ordenados, elija\(x = 4\) y\(x = 6\), luego calcule los valores de\(h(x)\).

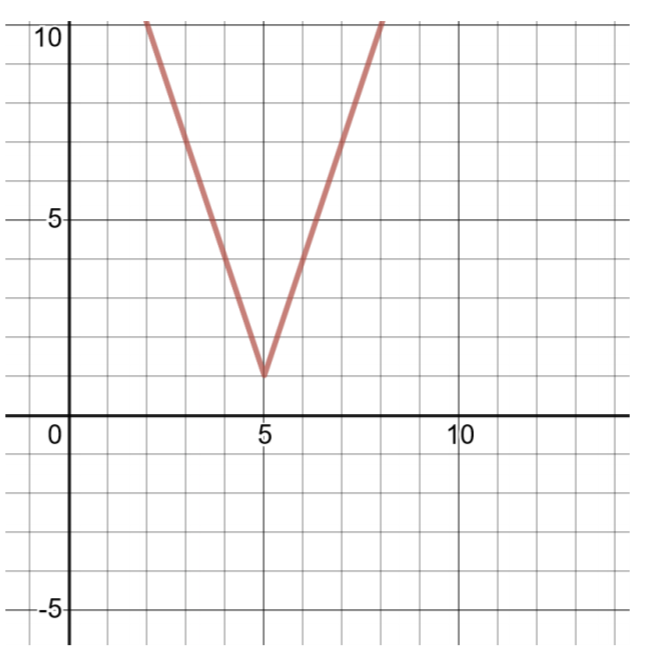
    clipboard_ee43f5a639ef847eb9b27a95bb4052b84.png
    Figura 4.5.3
    Tabla de soluciones para\(h(x) = 3\vert x − 5\vert + 1\)
    \(x\) \(h(x)\)
    4 \(g(−3) = \vert − 3 + 2\vert − 5 = \vert − 1\vert − 5 = 1 − 5 = −4\)
    5 \(g(−2) = \vert − 2 + 2\vert − 5 = \vert 0\vert − 5 = 0 − 5 = −5\)
    6 \(g(−1) = \vert − 1 + 2\vert − 5 = \vert 1\vert − 5 = 1 − 5 = −4\)
    Ejemplo 4.5.4

    Cree una tabla de soluciones y grafique la siguiente función de valor absoluto:

    \(h(x) = \dfrac{1}{2} \vert x − 2\vert + 3\)

    Solución

    Comparando esta función con la forma general para las funciones de valor absoluto (mostradas arriba),\(a = \dfrac{1}{2} \),\(h = 2\),\(k = 3\). El vértice es\((h, k)\) o\((2, 3)\).

    Para encontrar dos pares más ordenados, elija\(x = 1\) y\(x = 3\), luego calcule los valores de\(h(x)\).

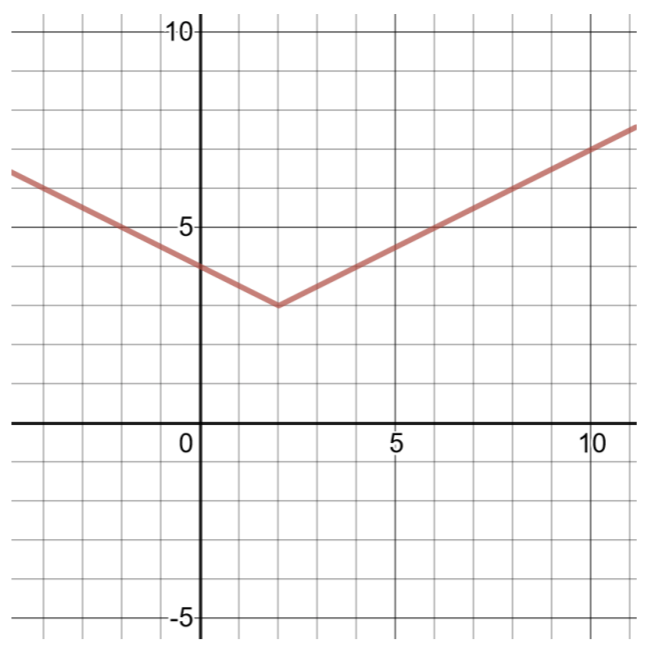
    clipboard_ecc69da60d6771932018e42e8e7a5cdda.png
    Figura 4.5.4
    Tabla de soluciones para\(h(x) = \dfrac{1}{2} \vert x − 2\vert + 3\)
    \(x\) \(h(x)\)
    1 \(h(1) = \dfrac{1}{2} \vert 1 − 2\vert + 3 = \dfrac{1}{2} \vert − 1\vert + 3 = \dfrac{1}{2} (1) + 3 = 3\dfrac{1}{2}\)
    2 \(h(2) = \dfrac{1}{2} \vert 2 − 2\vert + 3 = \dfrac{1}{2} \vert 0\vert + 3 = 0 + 3 = 3\)
    3 \(h(3) = \dfrac{1}{2} \vert 3 − 2\vert + 3 = \dfrac{1}{2} \vert 1\vert + 3 = \dfrac{1}{2} (1) + 3 = 3\dfrac{1}{2}\)
    Ejercicio 4.5.1

    Cree una tabla de soluciones y grafique las siguientes funciones de valor absoluto:

    1. \(f(x) = \vert x + 6\vert\)
    2. \(g(x) = \dfrac{1}{3} \vert x − 3\vert + 5\)
    3. \(h(x) = 4\vert x + 2\vert + 2\)
    4. \(f(x) = \vert x − 1\vert − 5\)

    This page titled 4.5: Funciones de Valor Absoluto is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Victoria Dominguez, Cristian Martinez, & Sanaa Saykali (ASCCC Open Educational Resources Initiative) .