Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

4.6: Funciones polinomiales

Última actualización

30 oct 2022
Guardar como PDF
- 4.5: Funciones de Valor Absoluto
- 4.7: Dominio y rango de una función

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Una Función Polinómica es una función que se puede escribir en la forma general:

$f(x) = a_n x^n + a_{n−1} x^{n−1 }+ ... + a_1x + a_0$

para $n$ un entero no negativo, llamado el grado del polinomio. Los coeficientes $a_0$ , $a_1$ , $\ldots$ , an son números reales con coeficiente principal an $a_n \neq 0$ . El dominio de una Función Polinómica es $(−\infty , \infty )$ . La gráfica de una función polinómica de grado $n$ puede intersectar el eje x en la mayoría de los $n$ casos. Estas son las raíces de la función polinómica.

No hay ejemplos ni tareas en esta sección.

Funciones cuadráticas

Definición: Una función de la forma

$f(x) = ax^2 + bx + c$ donde $a\neq 0$

es una función cuadrática en forma estándar, y su gráfica es una parábola. Cuando el coeficiente inicial, $a$ , es positivo, la gráfica de la Función Cuadrática se abre hacia arriba. Cuando el coeficiente inicial, $a$ , es negativo, la gráfica de la Función Cuadrática se abre hacia abajo.

Ejemplo 4.6.1

Esboce una gráfica de $f(x) = −x^2 + 5x + 3$ en un sistema de coordenadas rectangular. Encuentra el vértice, la (s) intersección (s) x y la intersección y algebraicamente.

Solución

Encuentra el vértice calculando $\left(\dfrac{-b}{2 a}, f\left(\dfrac{-b}{2 a}\right)\right)$ con $a = −1$ , $b = 5$ y $c = 3$ .

\ (\ begin {aligned}
\ left (\ dfrac {-b} {2 a}, f\ left (\ dfrac {-b} {2 a}\ right)\ right) &=&&\ text {Encuentra el vértice de la parábola}\
\ dfrac {-5} {2 (-1)} &=\
\ dfrac {5} {2} &=2.5 &&\ text {Simplificar}\\
\ dfrac {-5} {2 (-1)} &=2.5\\
f (2.5) &=- (2.5) ^ {2} +5 (2.5) +3=9.25=&& f\ left (\ dfrac {-b} {2 a}\ derecha) =9.25\\ izquierda (\ dfrac {-b} {2 a}, f\ izquierda (\ dfrac {-b} {2 a}\ derecha)\ derecha) & =( 2.5,9.25) &&\ text {Vértice de la parábola}
\ end {alineado}\)

Para encontrar las intercepciones:

\ (\ begin {aligned} 0&=-x^ {2} +5 x+3 &&\ text {x-intercept, set} f (x) =0\\ 0&=-x^ {2} +5 x+3 &&\ text {Usa la Fórmula Cuadrática para resolver esta ecuación (no se puede factorizar). Vamos} a=-1, b=5, c=3\\ x&=\ dfrac {-5\ pm\ sqrt {(5) ^ {2} -4 (-1) (3)}} {2 (-1)} &&\ text {Fórmula Cuadrática
}\\ x&=\ dfrac {-5\ pm\ sqrt {37}} {-2} &&\ text {Simplificar}\\
x&=-0.54\ text {or} x=5.54 &&\ text {Esta función cuadrática tiene dos raíces (intercepciones x). }\\ f (0) &=-0^ {2} +5 (0) +3 &&\ text {y-intercept, set} x=0\\ f (0) &=3 &&\ text {y-intercept}\ end {alineado}\)

Grafique los cuatro pares ordenados, y calcule más pares ordenados si es necesario: $(2.5, 9.25)$ , $(−.54, 0)$ , $(5.54, 0)$ , $(0, 3)$ .

Ejercicio 4.6.1

$f(x) = 2x ^2 − 5x − 5$
$f(x) = 0.5x ^2 − 6x + 21$
$f(x) = −4x ^2 − 8x − 3$
$f(x) = −4x^ 2 + 16x − 15$
$f(x) = x^ 2 − 8x + 12$
$f(x) = −7x^ 2 + 100x − 10$

Funciones cúbicas y de orden superior

Definición: Función cúbica

Una función cúbica es una función polinómica de tercer grado que se puede escribir en la forma general:

$f(x) = a_3x^ 3 + a_2x^2 + a_1x + a_0$

con 3 como el grado de la función cúbica. Los coeficientes $a_0$ , $a_1$ , $a_2$ , $a_3$ son números reales con coeficiente inicial $a_3 \neq 0$ . El dominio de una función cúbica es $(−\infty , \infty )$ .

Ejemplo 4.6.2

Factorizar si es posible y grafica la función creando una tabla de soluciones:

$f(x) = x^3 − 4x^2 + 6x − 1$

Solución

Este polinomio es de grado 3, y es difícil de factorizar. Crear una tabla de soluciones para graficar.

Tabla de soluciones para $f(x) = x^3 − 4x^2 + 6x − 1$
$x$	$f(x)$
-2	$f(−2) = (−2)^3 − 4(−2)^2 + 6(−2) − 1 = −37$
-1	$f(−1) = (−1)^3 − 4(−1)^2 + 6(−1) − 1 = −12$
0	$f(0) = (0)^3 − 4(0)^2 + 6(0) − 1 = −1$
1	$f(1) = (1)^3 − 4(1)^2 + 6(1) − 1 = 2$
2	$f(2) = (2)^3 − 4(2)^2 + 6(2) − 1 = 3$

Ejemplo 4.6.3

Factorizar si es posible y grafica la función creando una tabla de soluciones:

$g(x)=x^4-16$

Solución

Este polinomio es de grado 4, y debido a que es una diferencia de cuadrados, se puede factorizar en un producto de binomios para encontrar los ceros del polinomio. Crear una tabla de soluciones para graficar.

$\begin{aligned} g(x)&=\left(x^{2}-4\right)\left(x^{2}+4\right) && \text{Factoring into the sum and difference of binomials.} \\ g(x)&=(x-2)(x+2)\left(x^{2}+4\right) && \text{Further factoring. Set each binomial equal to zero to find the real number zeroes of the polynomial.} \\ x-2&=0, x=2 && \text{The first real number zero of the polynomial, }(2,0) \\ x+2&=0, x=-2 &&\text{The second real number zero of the polynomial, } (2,0) \\ x^{2}+4&=0, x^{2}=-4 && \text{The third binomial factor does not produce real number zeroes, } \\ & &&\text{because no number squared can result in a negative value.} \end{aligned}$

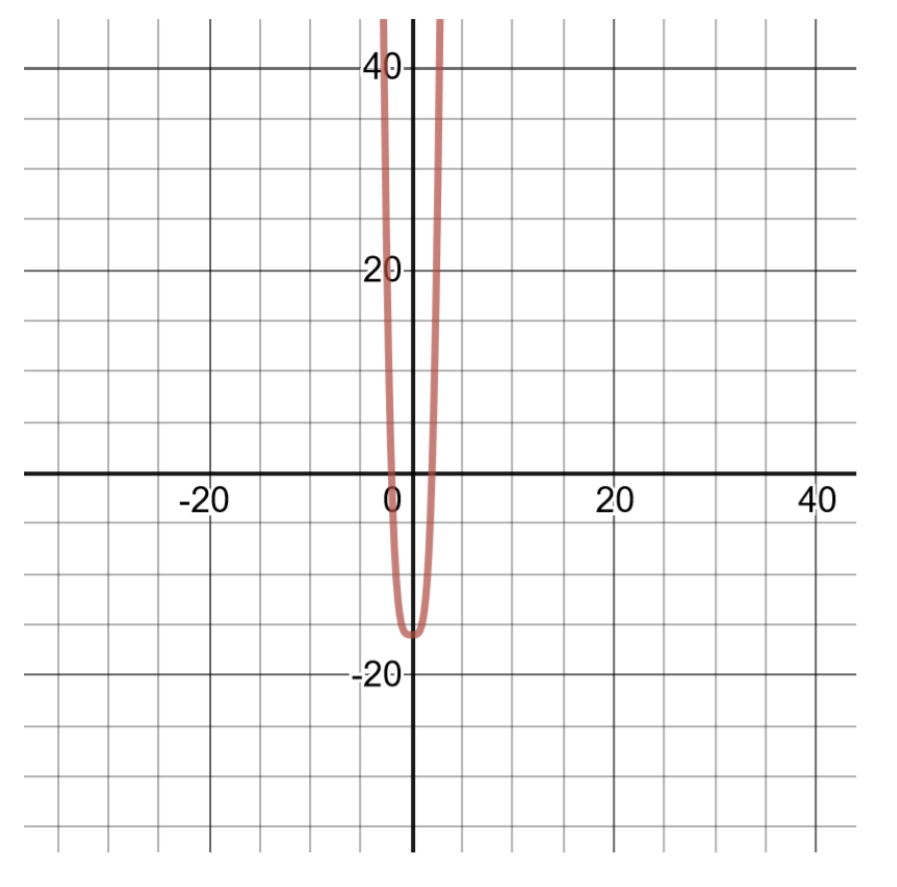
Tabla de soluciones para $g(x)=x^4-16$
$x$	$g(x)$
-2	$g(−2) = (−2)^4 − 16 = 16 − 16 = 0$
-1	$g(−1) = (−1)^4 − 16 = 1 − 16 = −15$
0	$g(0) = (0)^4 − 16 = 0 − 16 = −16$
1	$g(1) = g(1) = (1)^4 − 16 = 1 − 16 = −15$
2	$g(2) = g(2) = (2)^4 − 16 = 16 − 16 = 0$

Ejemplo 4.6.4

Factorizar si es posible y grafica la función creando una tabla de soluciones:

$f(x) = x ^6 − 5x ^2 + 3$

Solución

Este polinomio es de grado 6, y es difícil de factorizar. Crear una tabla de soluciones para graficar.

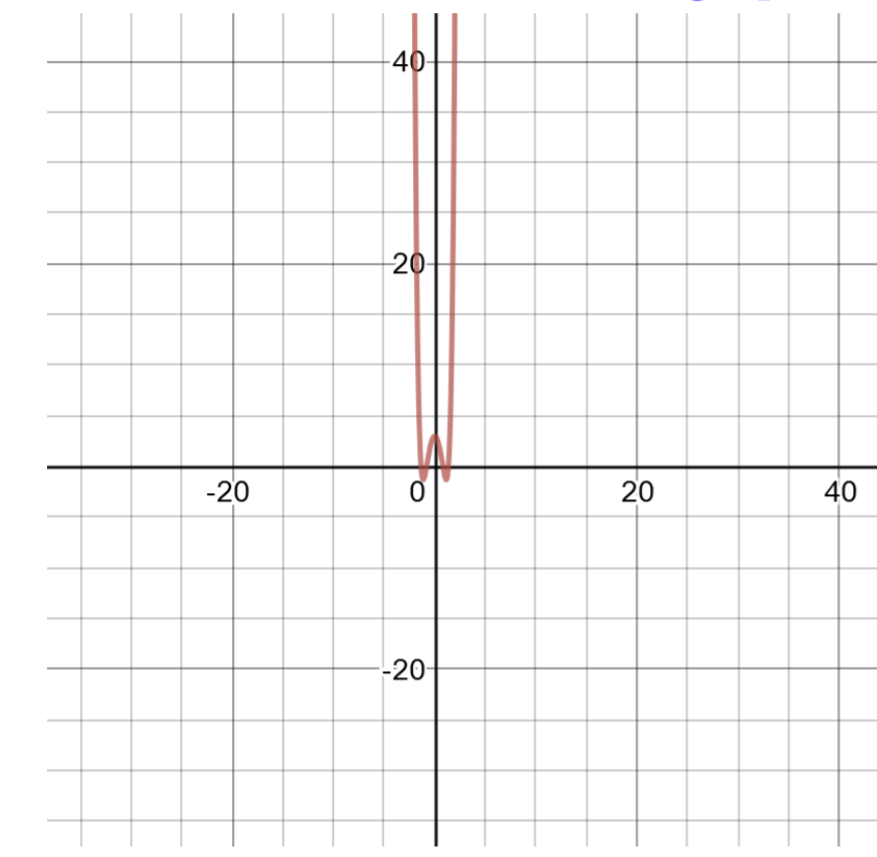
Tabla de soluciones para $f(x) = x ^6 − 5x ^2 + 3$
$x$	$f(x)$
-2	$f(−2) = (−2)^6 − 5(−2)^2 + 3 = 47$
-1	$f(−1) = (−1)^6 − 5(−1)^2 + 3 = −1$
0	$f(0) = (0)^6 − 5(0)^2 + 3 = 3$
1	$f(1) = (1)^6 − 5(1)^2 + 3 = −1$
2	$f(2) = (2)^6 − 5(2)^2 + 3 = 47$

Ejercicio 4.6.2

$f(x) = x^3 − 27$
$g(x) = 81x ^4 − 16$
$h(x) = 2x ^5 − 4x ^2 − 6x + 3$
$f(x) = 5x ^6 − 6x ^4 + 5$

Funciones racionales

Definición: Función racional

Una función racional es una función que puede escribirse como cociente de polinomios.

$f(x) = \dfrac{P (x) }{Q(x) }$ , $Q(x) \neq 0$

donde $P(x)$ y $Q(x)$ son polinomios en una variable $x$ . El dominio es el conjunto de todos los números reales tales que $Q(x) \neq 0$ .

Ejemplo 4.6.5

Para la función, $f(x) = \dfrac{9 }{x − 3}$ :

Graficar la función
Evaluar la función para $x = 0$ y $x = 2$

Solución

Preste atención al dominio de esta función. La división por cero es indefinida, por lo que el (los) número (s) que hará el denominador 0 deben ser excluidos del dominio.

En este problema, $x − 3$ está en el denominador de la función. Establecer $x − 3 = 0$ y resolver para $x$ . Si $x = 3$ la división es indefinida, entonces excluye el número 3 del dominio de la función. Piense en ello como siempre comenzando con todos los números reales $(−\infty , \infty )$ y luego eliminando los valores que provocarán una división indefinida.

El dominio de esta función es $(−\infty , 3) \cup (3, \infty )$ .

Las funciones racionales suelen tener asíntotas, una línea que se aproxima continuamente a una curva dada pero que no la encuentra a ninguna distancia finita. Aprenderás sobre las asíntotas en la sección Croquizado de Curvas de Matemáticas 162.

La gráfica de esta función se puede encontrar haciendo una tabla de soluciones:

Tabla de soluciones para $f(x) = \dfrac{9 }{x − 3}$	Dominio: $(−\infty , 3) \cup (3, \infty )$
$x$	$f(x)$
-4	$-\dfrac{9}{7}$
-3	$-\dfrac{3}{2}$
-2	$-\dfrac{9}{5}$
-1	$-\dfrac{9}{4}$
0	$-3$
1	$-\dfrac{9}{2}$
2	$-9$

Ejemplo 4.6.6

Para la función, $f(x) = \dfrac{100x}{ x^2 − 3x − 4}$

Graficar la función
Evaluar la función para $x = −1$ y $x = 3$

Solución

Preste atención al dominio de esta función. La división por cero es indefinida, por lo que el (los) número (s) que hará el denominador 0 deben ser excluidos del dominio.

En este problema, $x^2 − 3x − 4$ está en el denominador de la función. Factorizar la expresión cuadrática para obtener $(x − 4)(x + 1)$ y establecer cada factor igual a cero y resolver para $x$ : $x − 4 = 0$ , so $x = 4$ ; $x + 1 = 0$ , so $x = −1$ . Si $x = 4$ o $x = −1$ , la división es indefinida, así que excluye los números 4 y −1 del dominio de la función. Piense en ello como siempre comenzando con todos los números reales $(−\infty , \infty )$ y luego eliminando los valores que resultarán en una división indefinida.

El dominio de esta función es $(−\infty , −1) \cup (−1, 4) \cup (4, \infty )$ . La gráfica de esta función se puede encontrar haciendo una tabla de soluciones:

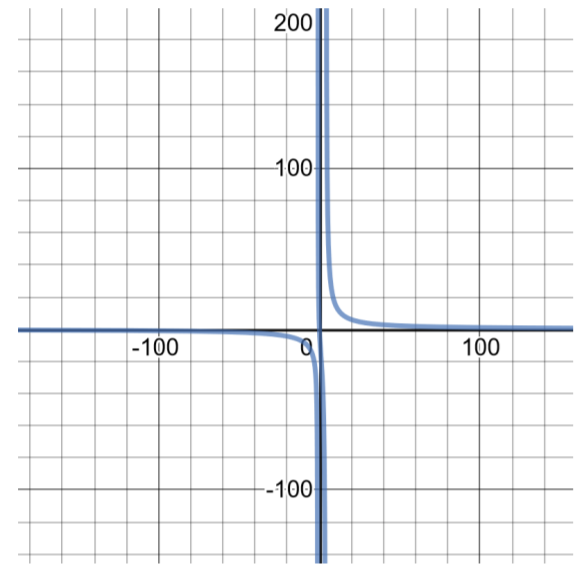
Tabla de soluciones para $f(x) = \dfrac{100x}{ x^2 − 3x − 4}$	Dominio: $(−\infty , −1) \cup (−1, 4) \cup (4, \infty )$
$x$	$f(x)$
-4	−16.667
-3	−21.429
-2	−33.333
-1	undefined
0	0
1	−16.667
2	−33.333
3	-75
4	undefined

Ejercicio 4.6.3

$f(x) = \dfrac{3x + 6 }{x − 1}$
$f(x) = \dfrac{9 }{x^2 − 9}$
$f(x) = \dfrac{x^ 2 − 4 }{x^2 − 4x}$

Funciones cuadráticas

Solución

Funciones cúbicas y de orden superior

Solución

Solución

Solución

Funciones racionales

Solución

Solución

Support Center

How can we help?