7.4: Ecuaciones de Líneas Verticales y Horizontales

Última actualización
Guardar como PDF

Page ID: 112462

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición: Línea vertical

La ecuación de una línea vertical es de la forma$x = c$, donde$c$ está cualquier número real. La línea vertical siempre cruzará el$x$ eje −axis en el punto$(c, 0)$. La pendiente de una línea vertical es indefinida.

Ejemplo 7.4.1

Encuentra la pendiente de la línea$x = 4$ y grafica la línea.

Solución

$x = 4$es la gráfica de una línea vertical como se muestra en la siguiente figura.

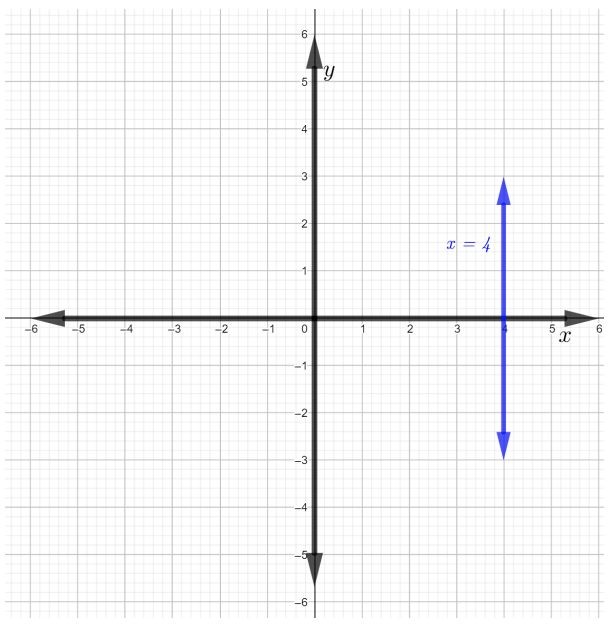
$clipboard_e96383c84992a62541d09b7ee1e53697f.png$

Para encontrar la pendiente de la línea,$x = 4$ elija dos puntos distintos en la línea. Que los puntos sean$(4, −1)$ y$(4, 3)$. Usando la pendiente de una fórmula de línea,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3 − (−1)}{4 − 4} &\text{Substitute values} \\ &= \dfrac{4}{0} &\text{Simplify} \end{array}$

Ahora bien, si$4$ se divide por$0$, esto equivale a hacer la pregunta”, ¿qué número por cero da$4$?” la respuesta es, no existe tal número. La división por cero no está definida, y la pendiente de la línea vertical$x = 4$ es indefinida.

Definición: Línea Horizontal

La ecuación de una línea horizontal es de la forma$y = k$, donde$k$ está cualquier número real. La línea horizontal siempre cruzará el$y$ eje −axis en el punto$(0, k)$. La pendiente de una línea horizontal es Cero.

Ejemplo 7.4.2

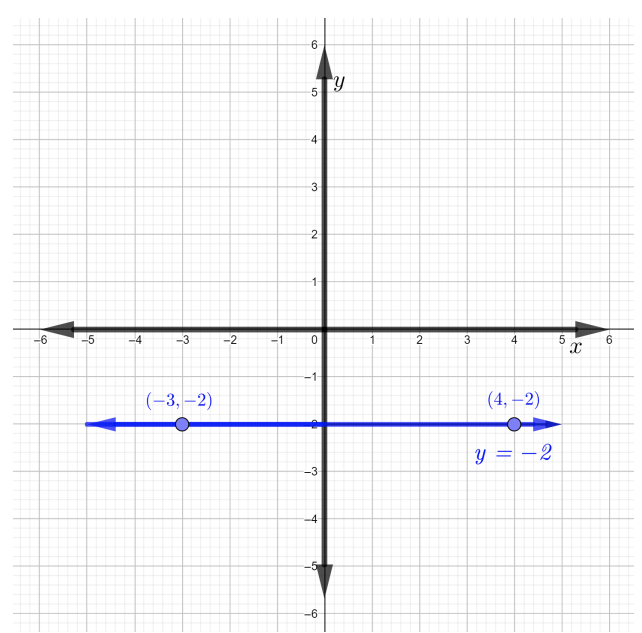
Encuentra la pendiente de la línea que pasa por los puntos$(−3, −2)$ y$(4, −2)$. Trazar los puntos y graficar la línea que pasa a través de ellos.

Solución

Utilice la pendiente de la fórmula de línea. Por lo tanto,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{(−2) − (−2)}{4 − (−3)} &\text{Substitute values} \\ &= \dfrac{0}{7} &\text{Simplify} \\ &= 0 &\text{\(0$dividido por cualquier número distinto de cero es igual a cero}\ end {array}\)

Por lo tanto, la línea que pasa por los dos puntos dados es una línea horizontal, con pendiente igual a cero, como se muestra en la siguiente figura.

$clipboard_e08cf4386944def611c6831ac921a6f6d.png$

Ejemplo 7.4.3

Grafica la línea$y − 3 = 0$ y encuentra su pendiente.

Solución

La línea se$y − 3 = 0$ puede escribir como$y = 3$ (agregar$3$ a ambos lados de la ecuación). La línea$y = 3$ es una línea horizontal, como se muestra en la siguiente figura.

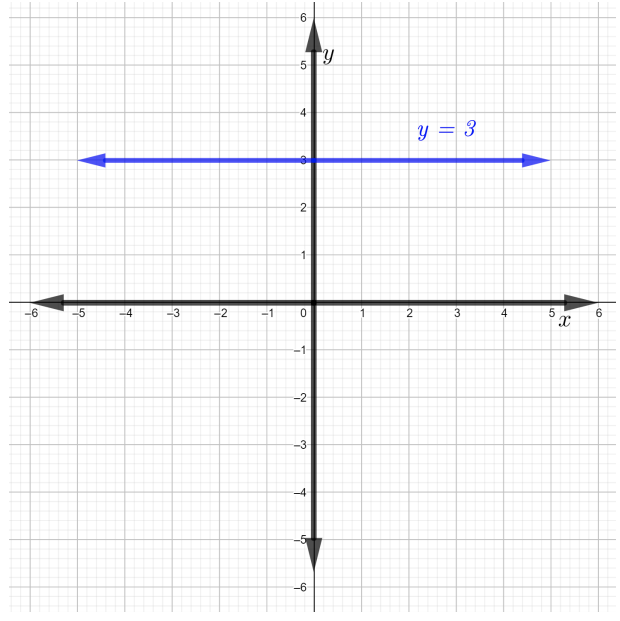
$clipboard_ef5d1c3aa2712f38f53b81ce34e7a1ee0.png$

Ahora, para encontrar la pendiente, elija dos puntos distintos en la línea$y = 3$. Considerar puntos$(0, 3)$ y$(3, 3)$. Por lo tanto,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3-3}{3-0} &\text{Substitute values} \\ &= \dfrac{0}{2} &\text{Simplify} \\ &= 0 &\text{\(0$dividido por cualquier número distinto de cero es igual a cero}\ end {array}\)

Por lo tanto, la pendiente de la línea dada es$m = 0.$

Ejercicio 7.4.1

Encuentra la pendiente de cada línea.

$x = −\dfrac{1}{2}$
$y − 1 = 0$
$x + 7 = 10$
$y + 2 = −9$
Encuentra la pendiente de la línea que pasa por los puntos$(−4, 1)$ y$(2, 1)$. Trazar los puntos y graficar la línea que pasa a través de ellos.
Encuentra la pendiente de la línea que pasa por los puntos$(−3, 5)$ y$(−3, −7)$. Trazar los puntos y graficar la línea que pasa a través de ellos.