7.5: Formas de la Ecuación de una Línea

Última actualización
Guardar como PDF

Page ID: 112474

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la sección anterior se explicaron las ecuaciones de líneas verticales y horizontales. Ahora descubre tres formas más de las ecuaciones de una línea, a saber, la Forma de Inclinación-Intercepción, la Forma Punto-Pendiente y la Forma Estándar.

Forma de pendiente-intercepción de la ecuación de una línea

Definición: Forma de pendiente-intercepción

La Forma Inclinación-Intercepción de la ecuación de una línea es de la forma:

\[y = mx + b \nonumber \]

Dónde$m$ está la pendiente de la línea y$(0, b)$ es el$y$ −intercept.

Tenga en cuenta que el$y$ -intercept es el punto donde la línea se cruza con el$y$ eje −, es decir, cuando$x = 0$.

Ejemplo 7.5.1

Escribe una ecuación de la línea con las pendientes e$y$ intercepciones dadas.

pendiente =$5$;$y$ −intercept$(0, \dfrac{1}{2})$
pendiente =$−\dfrac{5}{6}$;$y$ − intercepción$(0, −\dfrac{3}{4})$

Solución

$m = 5$y$b = \dfrac{1}{2}$

La ecuación de una línea es de la para$y = mx + b$. Por lo tanto,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= 5x + \dfrac{1}{2} &\text{Substitute \(m = 5$y$b = \dfrac{1}{2}$}\ end {array}\)

Por lo tanto,$y = 5x + \dfrac{1}{2}$ es la ecuación de la línea con la pendiente y$y$ -intercepción dadas.

Dado$m = −\dfrac{5}{6}$ y$b = −\dfrac{3}{4}$

Por lo tanto,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= −\dfrac{5}{6}x −\dfrac{3}{4} &\text{Substitute values} \end{array}$

Por lo tanto,$y = −\dfrac{5}{6}x − \dfrac{3}{4}$ es la ecuación de la línea con la pendiente y$y$ -intercepción dadas.

Ejemplo 7.5.2

Identifica la pendiente y$y$ −intercepta entonces, úsalos para graficar cada línea.

$y = −2x + 4$
$5y − 3x = 10$

Solución

a. Observe que la ecuación lineal dada está en forma de pendiente-intersección. Entonces,$m = −2$ o equivalentemente,$m = −\dfrac{2}{1}$ y$b = 4$

$m$es la pendiente de la línea, entonces$m = \dfrac{\text{rise}}{\text{run}} = −\dfrac{2}{1}$. Para graficar la línea, trazar al menos dos puntos. Comience en el$y$ −intercept$(0, 4)$ y mueva hacia abajo la$2$ unidad y luego muévase a la$1$ unidad derecha para trazar el segundo punto. Ahora une los dos puntos con una línea recta como se muestra en la siguiente figura.

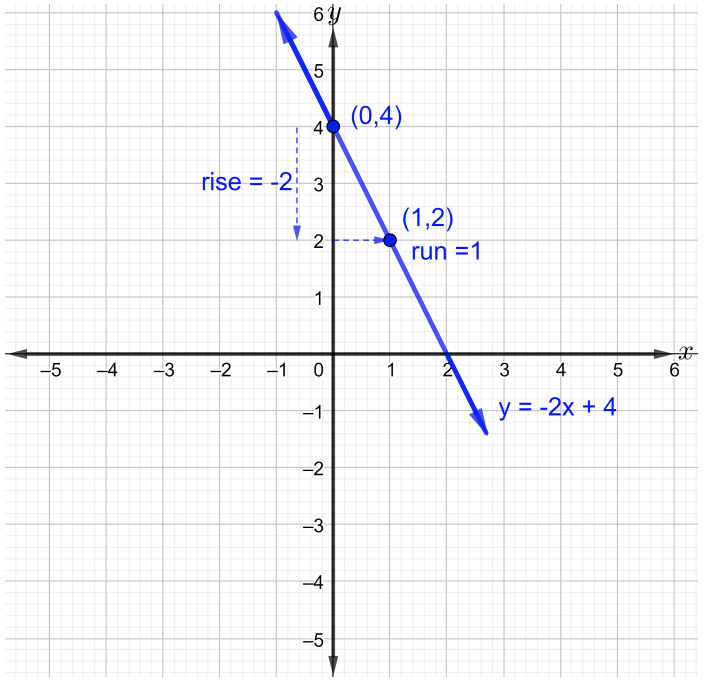
$clipboard_e5fcc0c548a6809df50a713b48295362a.png$

b. Observe que no está claro cómo identificar la pendiente e$y$ -intercepción en esta ecuación lineal dada porque no está en la forma pendiente-intercepción. Así, resolver$y$ para tener la ecuación en la forma pendiente-intersección de la siguiente manera,

$\begin{array} &&5y − 3x = −10 &\text{Given} \\ &5y = 3x − 10 &\text{Add \(3x$a ambos lados de la ecuación}\\ &y =\ dfrac {3} {5} x − 2 &\ text {Divide todos los términos por$5$ para aislar$y$}\ end {array}\)

Ahora,$m = \dfrac{3}{5}$ y$b = −2$. Comience trazando la$y$ -intercepción$(0, −2)$ luego mueva$3$ las unidades hacia arriba y$5$ las unidades a la derecha y trazar el segundo punto que es$(5, 1)$. Ahora, unir los dos puntos, es decir,$(0, −2)$ y$(5, 1)$ para obtener la gráfica de la línea que se muestra en la siguiente figura.

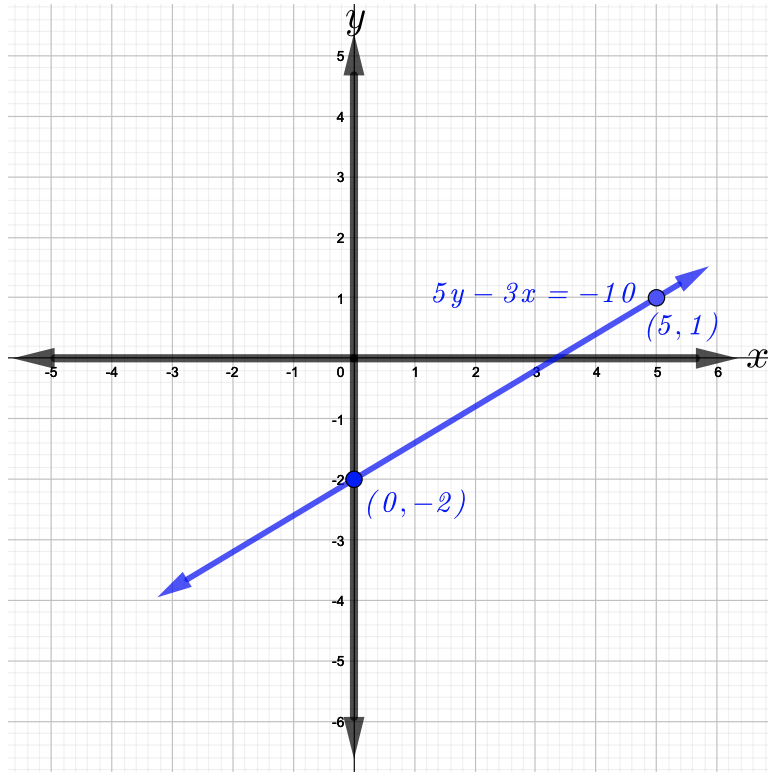
$clipboard_eca3205bebd002556f4570dc0193cd9f6.png$

Ejercicio 7.5.1

Escribir una ecuación de una línea con la pendiente dada y$y$ -interceptar.

pendiente:$2$$y$ -intercepción:$(0, \dfrac{3}{4})$
pendiente:$\dfrac{5}{7}$$y$ -intercepción:$(0, −6)$
pendiente:$−\dfrac{1}{2}$$y$ -intercepción:$(0, −\dfrac{7}{11} )$

Ejercicio 7.5.2

Identifica la pendiente e$y$ intercepta luego utilízalas para graficar cada línea.

$y = 5x − 3$
$2y = −6x + 1$

Forma Punto-Pendiente de la Ecuación de una Línea

Definición: Forma Punto-Pendiente

La Forma Punto-Pendiente de la ecuación de una línea recta es:

\[y − y_1 = m(x − x_1) \nonumber \]

Dónde$m$ está la pendiente de la línea y$(x_1, y_1)$ es cualquier punto en la línea recta.

Ejemplo 7.5.3

Encuentra la ecuación de cada línea que pasa por el punto dado y la pendiente dada.

Pendiente$3$ y punto$(−1, 8)$
Pendiente$−\dfrac{5}{2}$ y punto$(\dfrac{4}{3}, \dfrac{1}{3})$

Solución

Para encontrar la ecuación de la línea a través del punto$(−1, 8)$ con pendiente$m = 3$, utilice la forma punto-pendiente de la siguiente manera:

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 8 = 3[x − (−1)] &\text{Substitute \(m = 3$,$x_1 = −1$, y$y_1 = 8$}\\ &y − 8 = 3 (x + 1) &\ text {Simplificar}\\ &y − 8 = 3x + 3 &\ text {Multiplica ambos términos a la derecha de la ecuación por$3$}\\ &y = 3x + 11 &\ text {Agrega$8$ a ambos lados de la igualdad para aislar$y$}\ end {array}\)

Por lo tanto,$y = 3x + 11$ es la ecuación de la línea con la pendiente y el punto dados. La línea está en forma de pendiente-intercepción.

Similar a la parte a, use la Forma Punto-Pendiente de la siguiente manera:

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ & y−(−\dfrac{1}{3}) = −\dfrac{5}{2} (x −\dfrac{4}{3}) &\text{Substitute \(m = −\dfrac{5}{2},\;\; x_1 = \dfrac{4}{3}$, y$y_1 = −\dfrac{1}{3}$}\\ &y +\ dfrac {1} {3} = −\ dfrac {5} {2} x +\ dfrac {20} {6} &\ text {Distribuir y simplificar}\\ &y = −\ dfrac {5} {2} {2} x +\ dfrac {20} {6} −\ dfrac {1} {3} &\ texto {Tracto$\dfrac{1}{3}$ de ambos lados}\\ &y = −\ dfrac {5} {2} x + 3 &\ text {Para combinar las dos fracciones, observe que la pantalla LCD$= 6$.}\\ & &\ text {Multiplicar numerador y denominador de$\dfrac{1}{3}$ por$2$ y simplificar:}\\ & &\ text {$\dfrac{20}{6} − \dfrac{1(2)}{3(2)} = \dfrac{20}{6} − \dfrac{2}{6} = \dfrac{18}{6} = 3$}\ end {array}\)

Por lo tanto,$y = −\dfrac{5}{2}x + 3$ es la ecuación de la línea a través del punto de dar y la pendiente dada.

Ejemplo 7.5.4

Encontrar una ecuación de la línea dada puntos$(2, 4)$ y$(−3, 9)$.

Observe que anteriormente en este capítulo se explicó cómo encontrar una ecuación de una línea dada una pendiente y$y$ -intercepción. En este capítulo también se explicó cómo encontrar una ecuación de una línea dado cualquier punto de la línea y una pendiente. Entonces, en ambos métodos, se da la pendiente.

Solución

Para encontrar una ecuación de una línea dada dos puntos cualesquiera en la línea, primero busque la pendiente usando la pendiente de la fórmula de línea. Después, aplique la forma de punto-pendiente con cualquiera de los puntos dados. Primero, usa los dos puntos para encontrar la pendiente de la línea. Dejar$(x_1, y_1) = (2, 4)$ y$(x_2, y_2) = (−3, 9)$. Entonces,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Slope of the line formula} \\ &= \dfrac{9 − 4}{−3 − 2} &\text{Substitute values} \\ &= \dfrac{5}{−5} &\text{Simplify} \\ &= −1 & \end{array}$

Ahora se ha encontrado la pendiente así que a continuación se encuentra la ecuación de la línea utilizando cualquiera de los puntos dados. Así,$m = −1$ y considerar usar punto$(2, 4)$.

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-slope form} \\ &y − 4 = −1(x − 2) &\text{Substitute \(m = −1$,$x_1 = 2$,$y_1 = 4$}\\ &y − 4 = −x + 2 &\ text {Distribuir$-1$ a ambos términos a la derecha}\\ &y = −x + 6 &\ text {Añadir$4$ a ambos lados de la ecuación para aislar$y$}\ end {array}\)

Por lo tanto,$y = −x + 6$ es la ecuación de la línea que pasa por el punto de dar y tiene la forma pendiente-intercepción.

Ejercicio 7.5.3

Encuentra la ecuación de cada línea que pasa por el punto dado y tiene la pendiente dada.

La pendiente$−\dfrac{5}{2}$ y el punto$(3, 0)$.
La pendiente$\dfrac{1}{2}$ y el punto$(−2, −3)$.

Ejercicio 7.5.4

Encuentra una ecuación de la línea dada los siguientes Puntos.

$(−9, −3)$y$(6, −2)$
$(4, 1)$y$(−2, 2)$

Forma Estándar de la Ecuación de una Línea (AKA Forma General de una Ecuación Lineal)

Definición: Forma estándar

La forma estándar de una línea no vertical está en la forma

\[Ax + By = C \nonumber \]

Donde$A$ es un entero positivo,$B$ y$C$ son enteros con$B \neq 0$.

Ejemplo 7.5.5

Grafica cada línea de las siguientes ecuaciones:

$4x − 3y = 6$
$\dfrac{1}{2} − y + 1 = 0$

Tenga en cuenta que la$x$ -intercepción es el punto donde la línea se cruza con el$x$ eje. Es decir, cuándo$y = 0$. Así, la$x$ -intercepción es un punto de la forma$(a, 0)$, donde$a$ está cualquier número real.

Solución

La ecuación$4x − 3y = 6$ está en forma estándar. Para graficar la línea de la ecuación dada puede ser posible utilizar más de un método. Por ejemplo, resolviendo$y$ para obtener la ecuación en forma pendiente-intercepción, entonces, grafica la línea. También es posible encontrar dos puntos, luego graficar la línea. Los dos puntos más fáciles de encontrar rápidamente son los$x$ e$y$ intercepta. Entonces, se recomienda este método.

Para encontrar la$x$ -intercepción, establecer$y = 0$ en la ecuación dada y resolver para$x$ lo siguiente,

$\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4x − 3(0) = 6 &\text{Substitute \(y = 0$}\\ &4x = 6 &\ text {Simplificar}\\ &x =\ dfrac {6} {4} &\ text {Dividir por$4$ ambos lados de la ecuación}\\ &x =\ dfrac {3} {2} &\ text {Simplificar}\ end {array}\)

De ahí que la$x$ -intercepción sea el punto$(\dfrac{3}{2}, 0)$

Ahora, para encontrar la$y$ -intercepción, establecer de la$x = 0$ siguiente manera,

$\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4(0) − 3y = 6 &\text{Substitute \(x = 0$}\\ &−3y = 6 &\ text {Simplificar}\\ &y = 6 −3 &\ text {Dividir por$−3$ ambos lados de la ecuación}\\ &y = −2 &\ text {Simplificar}\ end {array}\)

Ahora, trazar los puntos$(\dfrac{3}{2}, 0)$ y$(0, −2)$ y graficar la línea recta que los atraviesa como se muestra en la siguiente figura.

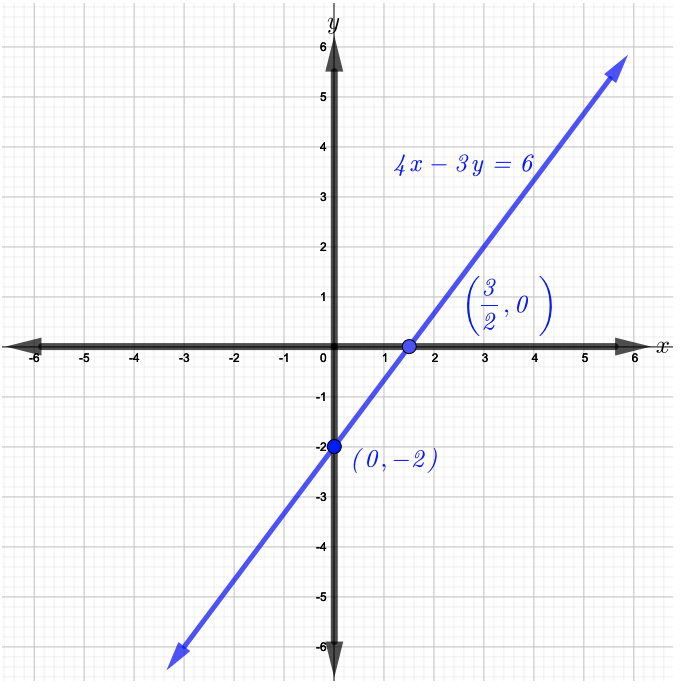
$clipboard_ede795f89eb03e5b448b62ec8dc0b7663.png$

La ecuación no$\dfrac{1}{2} x − y + 1 = 0$ está en forma estándar. Entonces, restar$1$ de ambos lados de la ecuación para tener$\dfrac{1}{2}x − y = −1$ que ahora está en forma estándar.

Nuevamente, similar a la parte b, encuentra las$y$ intercepciones$x$ y. Primero, encuentre la$x$ -intercepción configurando$y = 0$ y resuelva de la$x$ siguiente manera.

$ \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}x − (0) = −1 &\text{Substitute \(y = 0$}\\ &\ dfrac {1} {2} x = −1 &\ text {Simplificar}\\ &x = −2 &\ text {Multiplicar por$2$ ambos lados de la ecuación.} \ end {array}\)

Así, la$x$ -intercepción es el punto$(−2, 0)$.

Ahora, configurado$x = 0$ para encontrar la$y$ -intercepción, de la siguiente manera,

$ \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}(0) − y = −1 &\text{Substitute \(x = 0$}\\ &−y = −1 &\ text {Simplificar}\\ &y = 1 &\ text {Multiplicar por$-1$.} \ end {array}\)

De ahí que la$y$ -intercepción sea$(0, 1)$.

Trazar las$x$$y$ intercepciones$(−2, 0)$ y$(0, 1)$, luego graficar la línea recta que las atraviesa como se muestra en la siguiente figura.

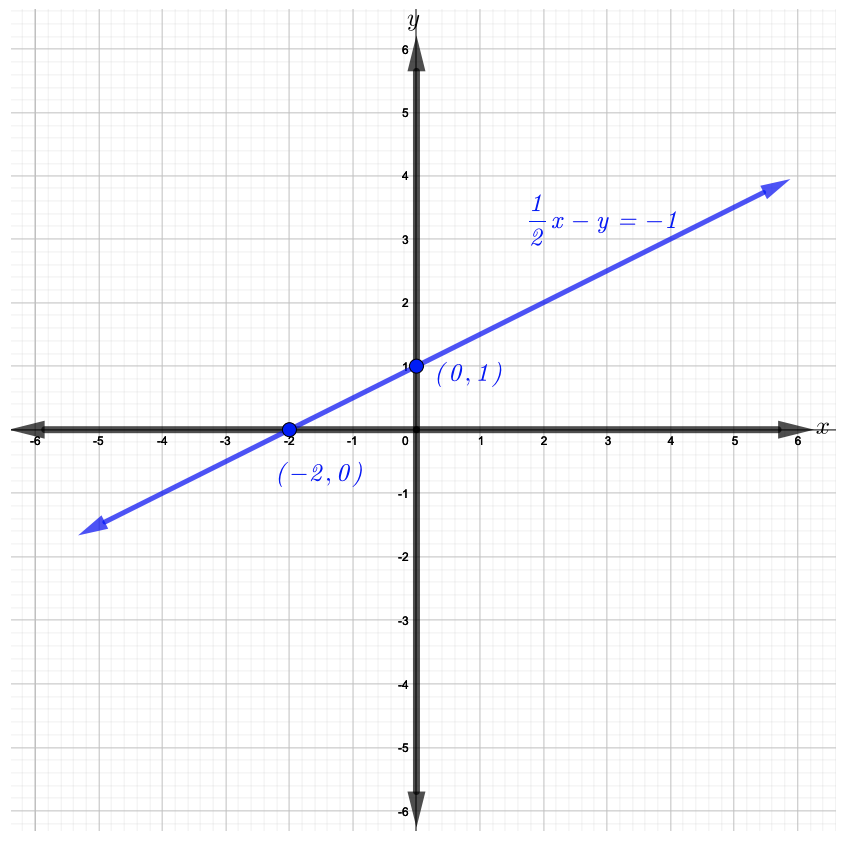
$clipboard_e3475016017c80b2298d3517f4bef3bf0.png$

No hay tarea para esta sección.