7.6: Ejemplos Aplicados

Última actualización
Guardar como PDF

Page ID: 112463

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para comprender mejor los conceptos aprendidos en este capítulo, aplíquelos a la situación de la vida real y a los problemas cotidianos.

Ejemplo 7.6.1

Las ventas totales de fundas para teléfonos en una popular tienda de teléfonos (en miles) se muestran en la siguiente figura. El mes de marzo,$2016$, corresponde a$x = 0$.

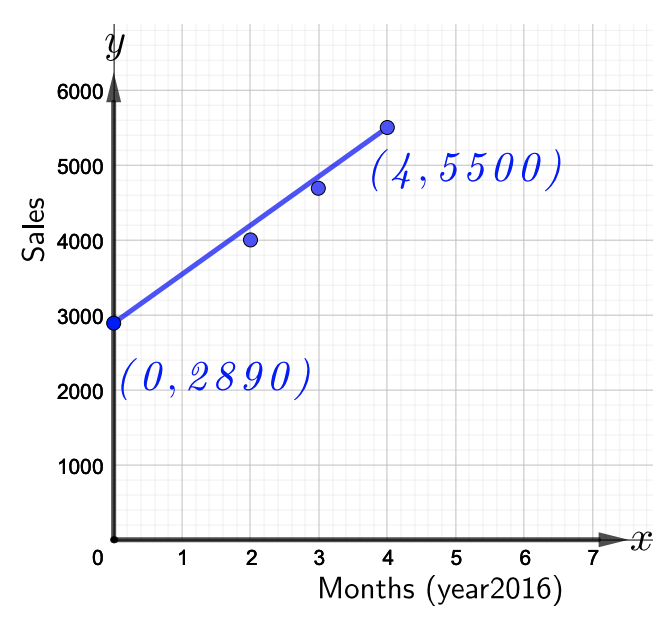
$clipboard_ee033c27bf4318e5b257e9c1d01d31895.png$

Consulte la figura anterior para escribir una ecuación de la línea que modela los datos. ¿Qué indica la pendiente?
Utilice la ecuación en la parte a para aproximar las ventas de cubiertas de teléfonos en el mes de noviembre,$2016$.

Solución

Refiriéndose a la cifra anterior, observe que hay dos puntos,$(0, 2890)$ y$(4, 5500)$, que se encuentran en la línea dada. Usa los dos puntos para encontrar primero la pendiente. Por lo tanto,

$m = \dfrac{5500 − 2890}{4 − 0} = \dfrac{2610}{4} = 652.5$

Así, la pendiente es$652.5$. Dado que la pendiente es positiva, indica un incremento. De ahí que la pendiente indique que las ventas de fundas para teléfonos han aumentado aproximadamente$$652.5$ por mes de marzo$2016$ a julio$2016$.

Utilice la pendiente y la$y$ -intercepción$(0, 2890)$ para escribir la ecuación de la línea en forma de pendiente-intercepción de la siguiente manera,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &y = 652.5x + 2890 &\text{Substituting \(m = 652.5$y$b = 2890$}\ end {array}\)

Ahora, se da que$x = 0$ corresponde al mes de marzo y el problema pide aproximar las ventas de fundas telefónicas en el mes de noviembre$2016$. Así,$x = 8$ corresponde al mes de noviembre$2016$. Sustituto$x = 8$ en la ecuación que se encuentra en la parte a. por lo tanto,

$\begin{array} &&y = 652.5x + 22980 &\text{Equation of the line from part a} \\ &= 652.5(8) + 2890 &\text{Substitute \(x = 8$}\\ &= 8110 &\ text {Multiplicar luego agregar para simplificar}\ end {array}\)

Por lo tanto, las ventas de fundas para teléfonos en el mes de noviembre$2016$ fueron aproximadamente$$8,110$.

Ejemplo 7.6.2

A una madre le preocupaba si su niño pequeño consume suficiente calcio. La principal ingesta de calcio del niño fue en forma de leche. La madre registró los datos durante nueve meses para monitorear la ingesta de leche del niño pequeño. Los datos se representan en un diagrama disperso que muestra la cantidad de leche que el niño consumió cada mes durante nueve meses, de febrero a octubre como se muestra en la siguiente figura.

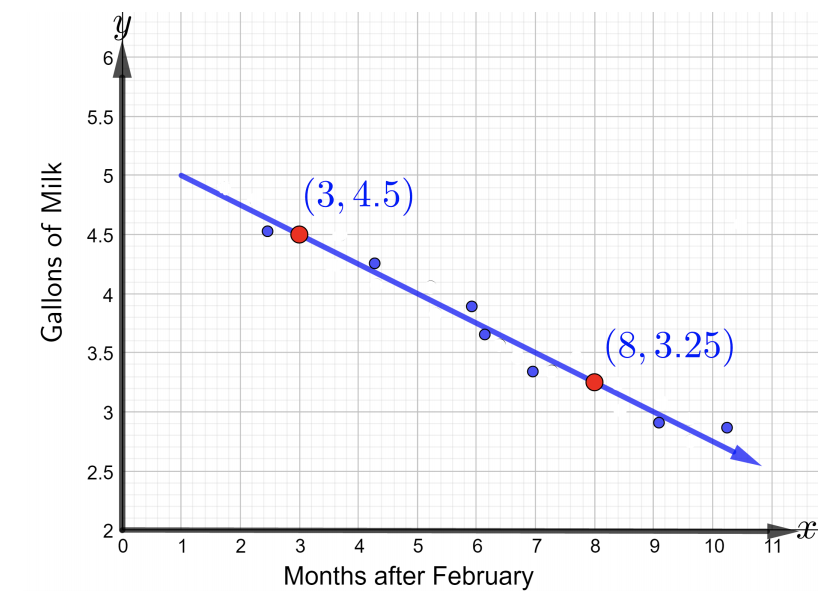
$clipboard_ec877e3e6b331b80db5f26dd301f14f22.png$

Consulte la figura anterior para escribir una ecuación de la línea para modelar los datos dados usando los dos puntos etiquetados. Escribe la ecuación en forma de pendiente-intercepción. ¿Qué se puede decir de la pendiente?
Utilice la ecuación de la línea que se encuentra en la parte a para predecir la cantidad de leve que consumirá el niño en diciembre.

Solución

Para escribir la ecuación de la línea, primero encuentra la pendiente usando los dos puntos etiquetados,$(3, 4.5)$ y$(8, 3.25)$. Por lo tanto,

$m = \dfrac{3.25 − 4.5}{8 − 3} = −\dfrac{1.25}{5} = −0.25$

La pendiente es negativa significa que el consumo de leche del niño está disminuyendo en aproximadamente$0.25$ galones de leche cada mes.

Dado que no se da la$y$ -intercepción, no será posible utilizar la forma de intercepción de pendiente. En su lugar, use la pendiente y cualquiera de los dos puntos etiquetados en la forma de pendiente de punto para encontrar la ecuación de la línea. Por lo tanto,

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 4.5 = −0.25(x − 3) &\text{Substitute \(m = −0.25$y punto$(3, 4.5)$ con$x_1 = 3$ y$y_1 = 4.5$}\\ &y−4.5 = −0.25x+0.75 &\ text {Distribuir$-0.25$ a ambos términos a la derecha}\\ &y = −0.25x + 5.25 &\ text {Agrega$4.5$ a ambos lados de la igualdad para resolver$y$ y obtener la ecuación en la forma pendiente-Intercepción }\ end {array}\)

Así,$y = −0.25x + 5.25$ es la ecuación de la línea que representa los datos dados en la figura anterior y está en forma pendiente-intercepción.

Para predecir cuántos galones de leche consumirá el niño en diciembre, primero encuentra$x$ que corresponde al mes de diciembre. Se da que$x = 0$ corresponde al mes de febrero. A partir del mes de marzo con$x = 1$,$x = 10$ corresponde al mes de diciembre. Sustituir$x = 10$ en la ecuación de la línea que se encuentra en la parte a y resolver de la$y$ siguiente manera,

$\begin{array} &&y = −0.25x + 5.25 &\text{Equation of the line found in part a} \\ &= −0.25(10) + 5.25 &\text{Substitute \(x = 10$}\\ &= −2.5 + 5.25 &\ text {Multiplica luego agrega para simplificar}\\ &= 2.75 &\ end {array}\)

Por lo tanto, el niño consumirá alrededor de$2.75$ galones de leche en diciembre.

Ejercicio 7.6.1

Las ventas anuales de cierto modelo de impresoras en una famosa tienda de electrónica se muestran en la siguiente figura, donde$2012$ corresponde el año$x = 0$.

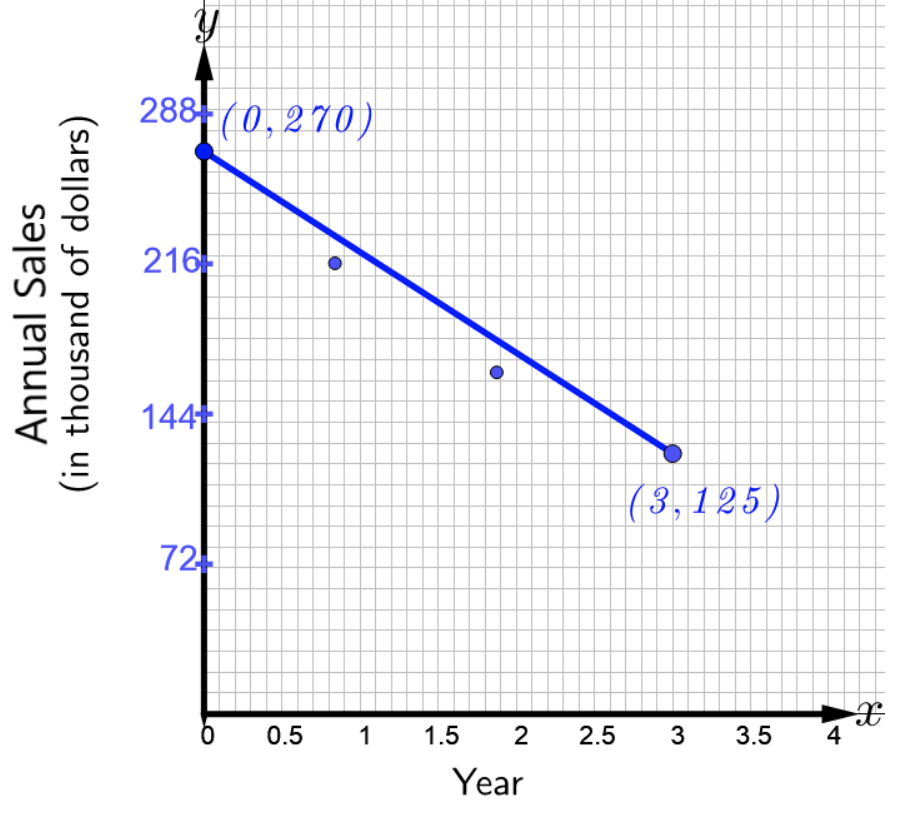
$clipboard_e91ed44b3227eee71555ff683b5007ce8.png$

Consulte la figura anterior para escribir una ecuación de la línea que modela los datos. ¿Qué indica la pendiente?
Utilice la ecuación de la línea que se encuentra en la parte a para aproximar las ventas de las impresoras en el año$2016$.

Ejercicio 7.6.2

John compró un cono de helado que mide$11.2$ cm de altura. Hacía mucho calor, el helado empezó a derretirse a razón de$2$ cm por minuto. John se interesó por lo rápido que se estaba derritiendo su helado y quería saber cuánto le quedaría después de$2.5$ minutos.

Encuentra una ecuación de la línea que modela los datos en forma de pendiente-intercepción.
Determinar la cantidad de helado que queda después de$2.5$ minutos.